蜗轮减速器振动信号特征提取与状态识别

白国振　周海宁

上海理工大学，上海，200092

蜗轮减速器振动信号特征提取与状态识别

白国振周海宁

上海理工大学，上海，200092

摘要：为实现蜗轮减速器运行状态识别，首先结合小波包分解和矩阵理论的特点，提出基于参考信号的小波包能量矩阵构造方法，分析了矩阵的最大奇异值(特征值)与运行状态的物理联系，并验证了所提方法比以往方法提取出的特征参数敏感度更高；然后改进思维进化算法(MEA)用于优化BP神经网络，实现对运行状态的智能识别，将提取的特征参数构成神经网络的输入向量，结果表明识别正确率提高了17.93%，从而验证了改进算法的优越性；最后提出了一种快速分类方法，该方法可以较好地区分故障与正常状态，解决了对实时性要求较高的在线诊断问题。

关键词：相对能量矩阵；特征提取；思维进化算法；识别

0引言

在工业上蜗轮减速器广泛应用于需要转换扭矩或速度的机械设备上。相比齿轮减速器，蜗轮减速器具有单级传动比大、体积相对较小且可实现自锁等优点，是设备动力传动的重要组成部件。所以，为了保证生产线连续运作，对蜗轮减速器的运行状态进行监测和诊断就显得尤为重要。

对机械设备运行状态识别的过程可以分为三个步骤：一是机械信号采集与获取；二是信号处理分析和特征提取；三是状态识别和故障诊断。信号处理方面，小波分析克服了传统时频分析的不足，其多分辨率的特点可以对信号进行多尺度细化分析，被普遍应用在故障诊断领域[1-3]。矩阵是高等代数中的常用工具，在工程应用中具有非凡的价值和意义，其特征参数往往蕴含着重要的信息[4-5]。因此，本文综合前人的经验和方法，结合小波包分解和矩阵理论的特点，提出一种基于参考信号的相对能量矩阵法来提取振动信号特征，然后用改进的思维进化算法对BP神经网络初始权值和阈值进行优化，将提取的特征参数构成特征向量作为神经网络的输入，以期实现对蜗轮减速器的运行状态识别。

1信号特征提取方法

小波包相对于小波的优点主要在于小波包能够对信号的高频部分做更加细致的刻画，因此小波包可以看作是小波的推广，具有更广泛的应用价值[6]。以一个二层分解进行说明，其小波包分解树结构如图1所示。A表示低频，D表示高频，后面的序数表示小波包分解的层数(即尺度数)。

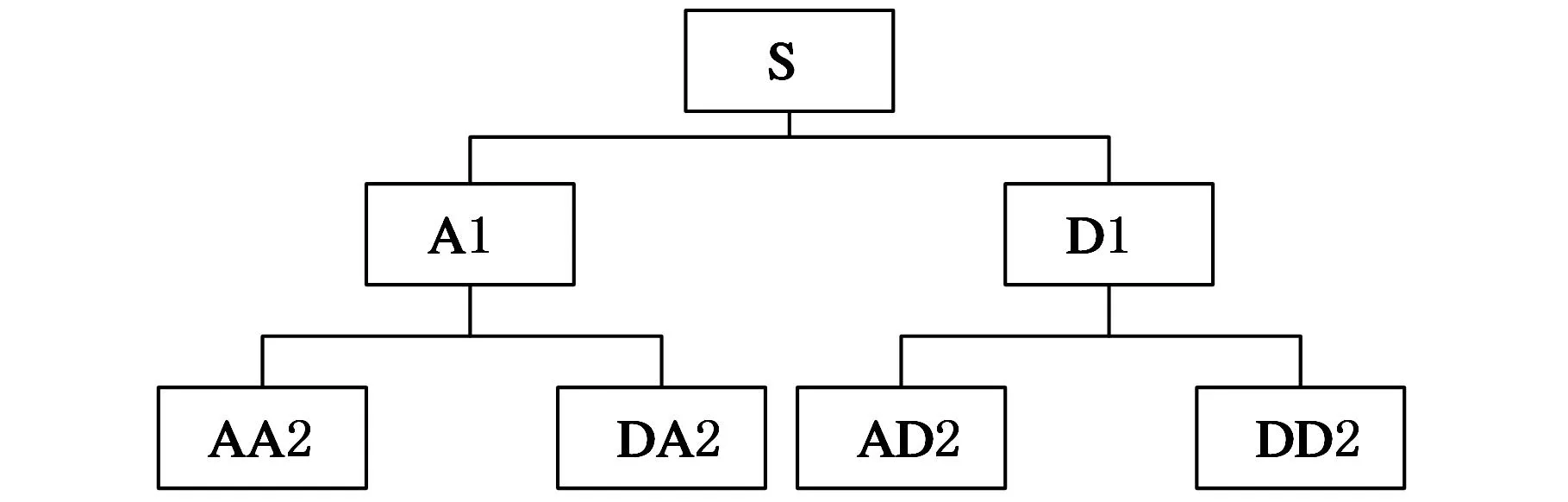
图1　小波包分解树

小波包分解能根据信号特性和分析要求自适应地选择相应频带与信号频谱进行匹配，是一种比小波分解更为精细的分解方法，尺度j越大，信号分解越细，且不同尺度的小波包分解系数不同程度地对应着信号的特征。文献[4]直接利用小波包分解系数构造特征矩阵，然后求其奇异值；文献[5]则用小波包分解系数导出各频段的能量来构造特征矩阵，然后求其特征值。这两种方法所用的振动信号都没有经过处理而直接进行小波包分解，这样就把与故障特征无关的噪声信号和平滑信号也引进了矩阵，故本文提出一种基于参考信号(正常信号)的小波包能量矩阵构造方法，以减少噪声信号和平滑信号的影响，最大程度地提取冲击信号特征。该方法称之为相对能量矩阵法，具体如下：

将振动信号与正常信号做矢量减法，所得的结果信号经j层小波包正交分解，得到2j个独立的分频段信号，再将各频段小波系数划分为2j个小带，分别计算各小带的能量，组成单频带矢量Eik(表示第i个频带第k个小带的能量，i=1，2，…，2j,k=1，2，…，2j),最后将各单频带矢量按行排列组成能量矩阵。采用小波包系数的平方和来表示所在频带的信号能量的大小,所构造的相对能量特征矩阵如下：

矩阵的特征值和奇异值分解在工程实际中有着广泛的应用[7-8]，它们能够充分反映矩阵的信息，也即从物理意义上表征着蜗轮减速器的运行状态特征。运用小波包分解系数可以很好地刻画信号所含特征，j越大，信号分解越细。但是随着j增大，所需要计算的矩阵维度越大，因此本文根据实际情况，选取分解层数j=3，小波基选用db4。

2验证与分析

搭建蜗轮减速器疲劳故障实验台，如图2所示。蜗轮减速器型号为WPA40，减速比为10，对蜗轮减速器常见故障进行模拟运行(在蜗轮上电火花加工出点蚀、磨损、断齿等故障)，采集振动信号。

图2　蜗轮减速器疲劳故障实验台

蜗杆转速控制在1500r/min，磁粉制动器加载扭矩为6N·m，信号采样频率设置为12 800Hz，采集的各运行状态下振动加速度信号如图3所示。

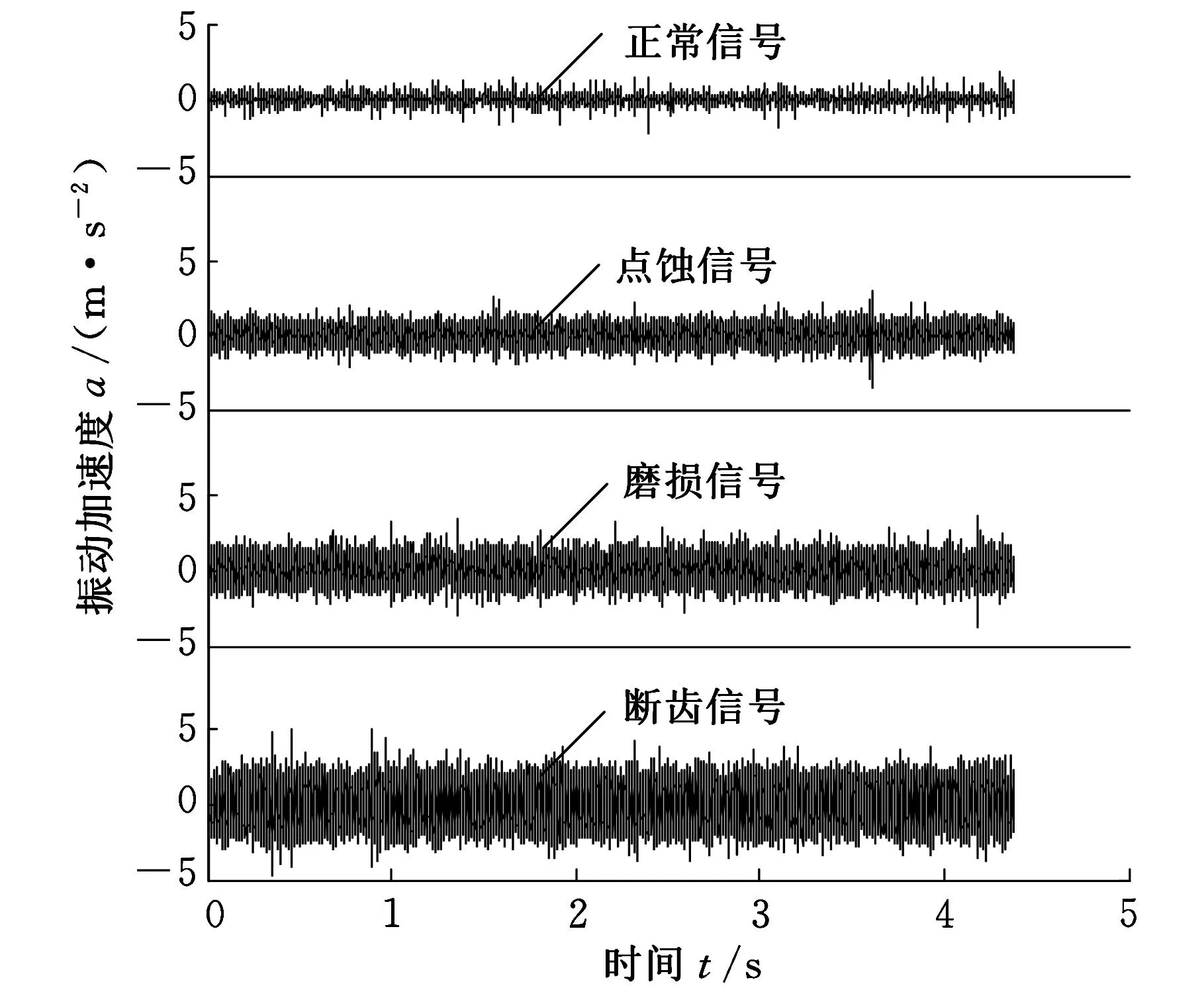
图3　振动信号

根据前文提出的信号特征提取方法，利用相对能量矩阵法构造矩阵，得到一个8×8的能量矩阵E。求取该矩阵的最大特征值和最大奇异值，并分别与文献[4-5]的方法进行横向对比，结果如表1所示(符号“//”前后分别为本文所提方法特征参数和文献[4-5]方法特征参数)。

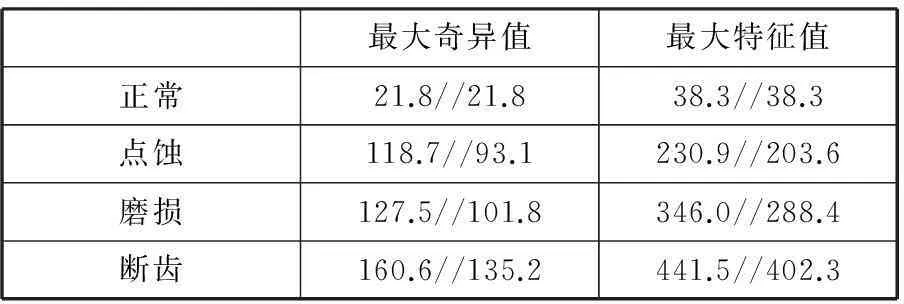
表1　矩阵特征参数对比

由表1可以看到，不同运行状态下矩阵的特征参数有较明显的变化：故障信号的参数比正常信号的参数大很多，因为随着故障的产生，蜗轮蜗杆振动加剧，信号的振幅增大，这从图3也可以解读出来；随着故障的恶化，振动愈来愈剧烈，信号表现出冲击性，能量增加，矩阵特征参数随着故障的加重也呈现出增大趋势，因此这两个特征参数可以较好地表征出蜗轮减速器的运动状态，且可以看出最大特征值比最大奇异值变化更明显。

另外，从对比结果可以看出，本文提出的基于参考信号的相对能量矩阵方法比直接用振动信号构建能量矩阵方法提取出的特征参数变化幅度更大更明显，表明相对能量矩阵法对运行状态变化的敏感度更高，从而验证了本文方法的优越性。因此可以用相对能量矩阵的奇异值和特征值来描述故障能量的变化，用于蜗轮减速器运行状态的识别。

3故障模式识别

3.1改进思维进化算法

思维进化算法(mind evolutionary algorithm，MEA)是孙承意等[9]于1998年提出的启发式随机搜索算法，其主要结构框架如图4所示。

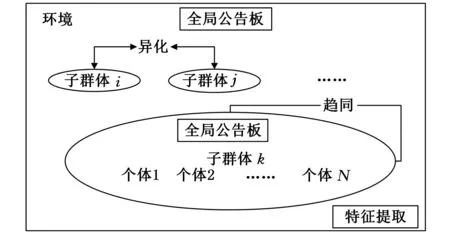
图4　MEA系统结构图

MEA把每一代中所有个体的集合称为一个群体，其基本思路是[10]：解空间内随机散布生成一定规模的个体，根据得分(反映个体对环境的适应能力)搜索出得分最高的若干个优胜个体和临时个体；分别以这些个体为中心，形成若干个优胜子群体和临时子群体；在子群体范围内，个体为了成为胜者而竞争的过程叫做趋同，一个子群体在趋同过程中，若不再产生新的胜者，则称该子群体已经成熟；当子群体成熟时，该子群体的趋同过程结束，并以该子群体中最优个体(即中心)的得分作为该子群体的得分。在整个解空间内，各子群体为了成为胜者而竞争，不断地探测解空间中新的点，这个过程叫做异化。

MEA作为一种进化算法，其自身不可避免地具有一般进化算法的一些缺陷。本文针对MEA个体搜索的局限性、补充淘汰临时子群体的随机性问题[11]，改进其趋同和异化操作策略，以期提高局部和全局的搜索效率和收敛性。

3.1.1趋同策略改进

MEA个体是在解空间内随机生成的，在传统的趋同过程中，个体散布宽度按照下式进行自适应调整[9]：

ω(i+1)d=c1ωid+c2δd

(1)

式中，i为迭代代数；ωid为第d维原有的个体散布宽度；δd为第d维两代新旧胜者之间的距离；c1、c2为常数。

为了提高算法的前期搜索能力，本文将MEA趋同策略进行如下改进：

(1)常数c1改为动态递减的方式，即

c1=cstart-(cstart-cend)i/Tmax

(2)

(2)c2改为

c2=c2r

(3)

式中，i为当前迭代代数；Tmax为最大迭代代数；cstart为初始散布权值；cend为迭代至最大次数时的散布权值；r为[0,1]间的随机数。

通过改进可使算法在迭代初期就具有较强的全局搜索能力从而改善MEA个体搜索的局限性问题，在迭代后期有利于进行更精确的局部开发来加快收敛速度。

3.1.2异化策略改进

异化操作是为了引导算法跳出局部而进行全局勘探，防止搜索被困在局部最优。优胜子群体与临时子群体间的替换、废弃以及子群体中个体释放的过程都是在异化操作中完成的。一个子群体被废弃意味着以一个新的个体为中心产生一个新的子群体。在传统MEA中，新的中心是在整个解空间中随机产生的，这样的策略虽然理论上能保证算法收敛于全局最优，但是由于抛弃了以前搜索中捕获的有用信息而重新搜索，导致算法效率和收敛速度大大降低。本文结合模拟退火算法(SA)[12]的特点，充分利用进化过程中捕获的信息，提出一种临时子群体的补充方法，即MEA异化策略改进算法，图5为算法简化流程图。算法步骤如下：

(1)按照MEA思路，执行趋同操作，得到较优(得分最高)的子群体G0。

(2)对G0以交叉概率Pc选择个体形成子群体G1,从G1中随机地选取个体Ni、Nj,按照下式进行变异扰动，产生新的个体：

(4)

式中，p为[0,1]之间的随机数。

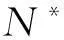
(4)如果迭代达到最大迭代次数或预设精度,则输出全局最优；否则更新退火温度T←αT，α∈(0.5,0.95)，更新迭代次数t←t+1,返回步骤(2),算法继续。

图5　MEA异化策略改进算法流程图

3.2模型的确立

本文诊断模型的主框架是基于BP神经网络的模式识别，利用改进的思维进化算法(improved mind evolutionary algorithm，IMEA)优化网络初始权值和阈值，以提高诊断的正确率。

对于一个m×n(设m≤n)的矩阵来说，一共有m个奇异值，而矩阵每一行的能量是与相应的奇异值成正比的，如果仅仅选择最大奇异值作为特征，则相当于仅仅将小波包能量最大的那个频道的能量作为特征，而其他所有频道的信息都丢弃了，这样就失去了利用小波包来分解信号的意义。且能量矩阵一定程度上受小波基和分解层数的影响[13]，进而对特征参数造成波动，所以本文提取矩阵的最大特征值、最大奇异值、平均特征值和平均奇异值作为四维特征向量输入，综合利用小波包各频带的信息，较以往文献中单一的特征参数更具有可靠性。因此，可以确立蜗轮减速器运行状态识别模型，即IMEA_BP诊断模型，如图6所示。

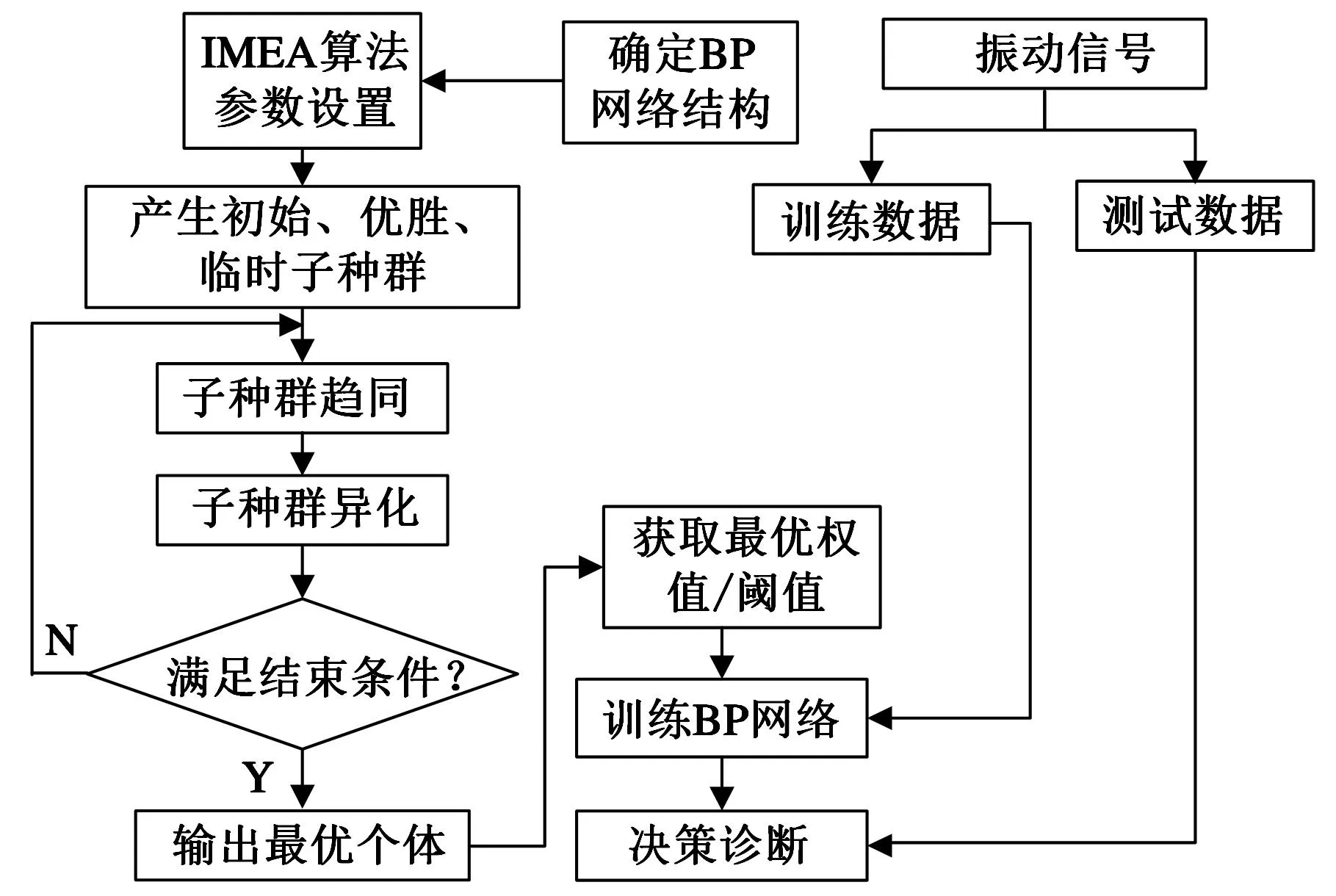
图6　IMEA_BP诊断模型流程图

3.3模型的验证

为了进行横向比较，分别用未经过优化的BP神经网络诊断模型BP、MEA优化的BP神经网络诊断模型MEA_BP、IMEA优化的BP神经网络诊断模型IMEA_BP三种诊断模型对同一数据库进行状态的识别。

(1)BP诊断模型的参数设置。输入层神经元个数S1=4，隐含层神经元个数S2=8，输出层神经元个数S3=4，最大迭代次数iiter=200。

(2)MEA_BP诊断模型的参数设置。除上述BP诊断模型的参数设置外，还设置种群大小Spop=200，优胜子种群个数Sbest=5，临时子种群个数Stemp=5，子种群大小SG=20。

(3)IMEA_BP诊断模型的参数设置。除上述MEA_BP诊断模型的参数设置外，设置交叉概率Pc=0.8，退火初始温度T0=100 000，降温系数α=0.9，退火结束条件为迭代误差达到10-5或者迭代次数达到1000次。

对每个运行状态下振动信号取500个训练数据，100个测试数据。正确率的比较结果如表2所示(10次识别的平均值)。

表2　不同诊断模型结果比较　%

对比发现，IMEA_BP诊断模型的正确率要明显优于其他两个诊断模型，且可以计算得到三种诊断模型的总正确率依次为73.15%、80.75%、91.08%，经过改进后的诊断模型正确率提高了17.93%，表明了IMEA_BP算法的有效性和优越性。诊断过程迭代曲线如图7所示，可以看出IMEA_BP算法的收敛速度优于其他两种算法。

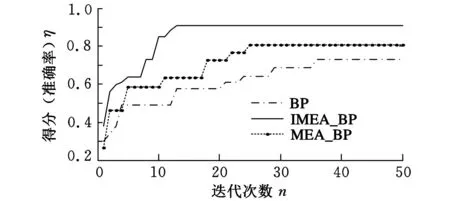
图7　迭代过程曲线

4快速诊断算法

神经网络是一种很好的智能模式识别方法，但是它需要经过一系列的学习和算法运算才能判断结果，这对于要求实时监测性的工程项目来说是一个很难取舍的问题。为此提出一种快速分类算法，通过直接观察特征参数来判断蜗轮减速器运行状态。

相对能量矩阵的最大特征值可以很好地表征蜗轮减速器振动信号的特征，因此考虑利用工程上常用的3σ法则即最大特征值置信区间来区分蜗轮减速器的运行状态。当最大特征值在某一故障值区间时则认为发生了该故障，这就需要引入一个置信概率的问题。根据概率论中切比雪夫不等式，设随机变量X存在数学期望和方差分别为μ和σ，则对于任意kσ>0，有

P(|X-μ|

(5)

k=3时表示小波熵值落在偏离期望均值3倍的标准差的范围内的样本概率即数值分布在(μ-3σ，μ+3σ)中的概率为0.9974。根据各类运行状态下的均值和标准差设置各种状态的置信区间，落在该类的μ±3σ范围内则运行状态属于该类，实验采集的数据各类状态取100组，求其能量矩阵最大特征值的均值和标准偏差，结果如表3所示。

表3　不同状态置信区间

从表3中可以看到，正常信号的置信区间和其他状态的区间距离较大，故可以很好地区分故障和正常状态，这在实际生产中具有重要的意义。故障信号(点蚀、磨损和断齿)之间的区间距离相差不是很大，但没有重叠，说明在一定程度上，利用状态的置信区间可以达到快速识别的目的。图8为各状态所取的100组信号构造的能量矩阵最大特征值及置信区间划分。

图8　各状态置信区间

5结语

(1)针对蜗轮减速器振动信号特点，提出了相对能量矩阵法，定义特征参数，实现了振动信号的特征提取。分析对比了以往能量矩阵的构造方法，证明了相对能量矩阵法的可行性及优越性。

(2)分析了传统思维进化算法的优缺点，通过动态改变常数权值并与模拟退火算法相结合，改进思维进化算法趋同和异化操作策略，提高了局部和全局的搜索效率和收敛性。将改进思维进化算法用于蜗轮减速器的故障诊断，达到了较好的效果。

(3)提出了一种快速诊断方法，解决了对实时性要求较高的应用问题，可以很好地将故障与正常状态区别开，有利于实现在线智能诊断。

参考文献：

[1]钟先友，赵春华，田红亮,等. 基于自适应最大相关峭度解卷积和频率切片小波变换的齿轮故障特征提取[J].中国机械工程,2014,25(21):2880-2885.

Zhong Xianyou, Zhao Chunhua, Tian Hongliang, et al. Gear Fault Feature Extraction Method Based on Adaptive MCKD and FSW[J]. China Mechanical Engineering, 2014, 25(21):2880-2885.

[2]王冬云,张文志. 基于小波包变换的滚动轴承故障诊断[J]. 中国机械工程,2012,23(3):295-298.

Wang Dongyun, Zhang Wenzhi. Fault Diagnosis Study of Ball Bearing Based on Wavelet Packet Transform[J]. China Mechanical Engineering, 2012, 23(3):295-298.

[3]李小玉，何怡刚，李目，等.基于小波分析和遗传神经网络的模拟电路故障诊断方法[J].计算机应用研究,2011,28(12):4517-4519.

Li Xiaoyu, He Yigang, Li Mu, et al. Wavelet Decomposition and Genetic Algorithm Based Approach for Fault Diagnosis of Analog Circuits[J]. Application Research of Computer, 2011, 28(12):4517-4519.

[4]李国宾，关德林，李廷举. 基于小波包变换和奇异值分解的柴油机振动信号特征提取研究[J]. 振动与冲击，2011,30(8):149-152.

Li Guobin, Guan Delin, Li Tingju. Feature Extraction of Diesel Engine Vibration Signal Based on Wavelet Packet Transform and Singularity Value Decomposition[J]. Journal of Vibration and Shock, 2011, 30(8):149-152.

[5]齐俊德,李山,陈冰. 基于小波包能量矩阵的轴承信号特征提取[J]. 振动与冲击,2013,32(21):107-111.

Qi Junde, Li Shan, Chen Bing.Feature Extraction of Bearing Vibration Signals Based on Wavelet Energy Matrix[J]. Journal of Vibration and Shock, 2013,32(21):107-111.

[6]花汉兵.基于小波包的振动信号去噪应用与研究[J]. 噪声与振动控制，2007(6):19-21.

Hua Hanbing. Application and Research of De-noising of Vibration Signal Based on Wavelet Packet[J]. Noise and Vibration Control, 2007(6):19-21.

[7]Shin K,Feraday S A,Harris C J,et al.Optimal Autoregressive Modelling of a Measured Noisy Deterministic Signal Using Singular-value Decomposition[J].Mechanical Systems and Signal Processing 2003,17(2):423-432.

[8]Yang W X,Peter W T.Development of an Advanced Noise Reduction Method for Vibration Analisis Based on Singular Value Decomposition[J].NDT&E International,2003,36(6):419-432.

[9]孙承意,孙岩,谢克明,等.思维进化——高效率的进化计算方法[C]//第三届全球智能控制与自动化大会论文集.合肥: 中国科学技术大学,2000:118-121.

[10]王小川，李洋，郁磊，等.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013.

[11]刘建霞，李楠，谢克明. 改进的思维进化算法在阵列天线综合中的应用[J]. 测试技术报,2009,23(4):331-336.

Liu Jianxia, Li Nan, Xie Keming. Application of Improved Mind Evolutionary Algorithm to Antenna Arrays Synthesis[J]. Journal of Test and Measurement Technology, 2009,23(4):331-336.

[12]Papadimtrou C H,Steiglitz K.Combinatorial Optimization:Algorithms and Complexity[M].Upper Saddle River,NJ:Prentice-Hall,1982.

[13]赵学智,叶邦彦,陈统坚. 矩阵构造对奇异值分解信号处理效果的影响[J]. 华南理工大学学报(自然科学版),2008,36(9):86-93.

Zhao Xuezhi, Ye Bangyan, Chen Tongjian. Influence of Matrix Creation Way on Signal Processing Effect of Singular Value Decomposition[J]. Journal of South China University of Technology (Natural Science Edition), 2008,36(9):86-93.

(编辑苏卫国)

Vibration Signal Feature Extraction and State Recognition for Worm Reducer

Bai GuozhenZhou Haining

University of Shanghai for Science and Technology,Shanghai,200093

Abstract:To achieve state recognition of worm reducer running state, a method of constructing wavelet packet energy matrix was proposed firstly based on reference signal. This was done by combining the characteristics of wavelet packet decomposition and matrix theory. It analyzed the intrinsic physical relationship between the maximum singular value (eigenvalue) and operating conditions. The results validate that the feature parameters extracted by this method is more sensitive than that by conventional ways. Secondly, the MEA was improved to optimize BP neural network. The fault characteristic parameters were extracted as the input feature vectors of neural network to realize the recognition of worm gear reducer states. The experimental results show that correct diagnosis rate increases 17.93 percent, which indicates the superiority of improved algorithm. A fast classification method was presented, which can solve the problems of on-line diagnosis for real-time requirements by distinguishing between normal and failure states well.

Key words:relative energy matrix; feature extraction; mind evolutionary algorithm (MEA); recognition

收稿日期：2015-05-12

基金项目：上海市自然科学基金资助项目(12ZR1420700)

中图分类号：TP39

DOI：10.3969/j.issn.1004-132X.2016.03.012

作者简介：白国振，男，1967年生。上海理工大学机械工程学院副教授。主要研究方向为信号处理与测试技术。周海宁，男，1990年生。上海理工大学机械工程学院硕士研究生。