基于模态应变能原理的简支钢梁损伤识别研究

薛刚，苏天，王崇阁

内蒙古科技大学建筑与土木工程学院，内蒙古包头014010



基于模态应变能原理的简支钢梁损伤识别研究

薛刚，苏天*，王崇阁

内蒙古科技大学建筑与土木工程学院，内蒙古包头014010

摘要：为解决目前多数梁式结构的损伤识别方法精度不足，且缺少模型试验对数值模拟结果进行验证等问题，利用模态应变能原理，运用数值分析和试验研究的方法对简支工字形钢梁的损伤识别进行研究。研究结果表明：模态应变能法可识别出简支梁内部的损伤；与通过固有频率变化的损伤识别相比，模态应变能法在梁损伤位置及损伤程度识别方面具有明显优势。

关键词：模态应变能；简支钢梁；损伤识别；有限元分析

土木工程结构在长达数十年的服役过程中，由于荷载作用、环境侵蚀、材料老化以及自然灾害等原因不可避免导致结构损伤［1］。大型的工程结构一旦出现严重的破坏事故，将对人类生命安全和财产安全造成巨大的损失，也会对社会产生不可估量的影响。传统的检测方法不仅耗费人力、物力，还可能对工程结构本身造成一定程度的损害。而利用振动特性对工程结构的损伤进行识别，对结构本身没有任何损害，且不影响结构的正常使用。其基本原理为［2］：结构的局部损伤通常会引起结构物理参数的变化，而模态参数是建立在结构物理参数基础上的，当工程结构的物理参数发生变化时，在此基础上的模态参数也会随之发生变化。通过建立二者之间的关系，即可达到损伤识别的目的。

本文基于模态应变能原理，对简支工字钢梁的损伤识别问题进行了数值分析，通过在每种工况下设定不同的损伤程度，考察模态应变能法对于简支梁几种典型损伤的识别效果；对简支工字钢梁的损伤识别问题进行动力试验研究，在每种损伤工况下对试验梁进行动态测试，获得梁的固有频率和模态振型，然后采用固有频率和单元损伤变量指标对简支梁的预设损伤进行识别，并对识别结果进行分析。对模态应变能法在简支钢梁损伤识别中的应用进行了探讨。

1　基本原理

1997年吴波［3］等首次将损伤变量的概念由材料领域推广到了构件和结构。对于一般的弹塑性材料，其沿轴向的损伤度可定义为［4］：

式中E——未发生损伤时材料弹性模量；

E（t）——发生损伤时材料有效弹性模量。

根据应变等效原理，结构单元t时刻的应变能耗散率可表示为：

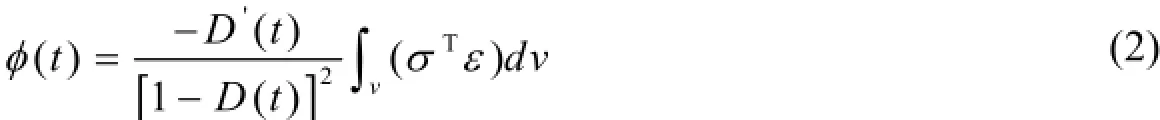
式中σ——结构内部某点的应力向量；

Ɛ——该点的应变向量；

T——矩阵的转置；

v——单元体积。

由于结构发生损伤时质量变化并不明显，因此只考虑其局部刚度的降低。定义结构损伤前后任一单元j关于第i阶模态的应变能为［5］：

Kj——单元j的刚度矩阵。

单元j在结构损伤前后的前n阶模态应变能之和分别为：

以结构无损伤时单元模态应变能的耗散过程来考虑损伤的出现与累积，则结构损伤过程中，单元j的模态应变能耗散率为：

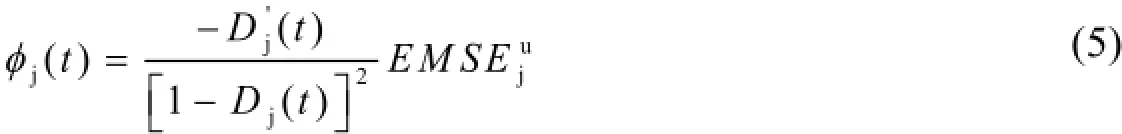
从式（5）可以看出，t=0时，Dj（0）=0，此时表示结构处于无损状态。对于脆性材料破坏过程，当损伤出现后可设损伤变量Dj（t）与时间t为线性关系［6］，则D'j（t）为一常数。当t=td时，损伤结构j单元的模态应变能变化量为：

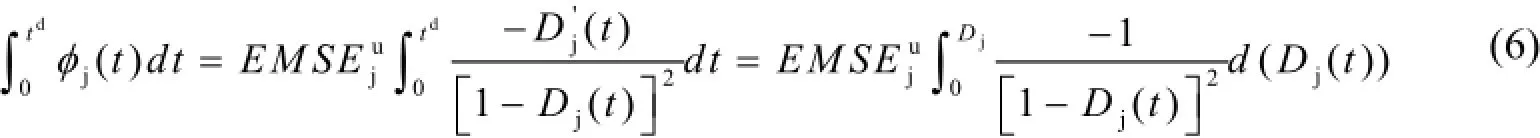
又因为：

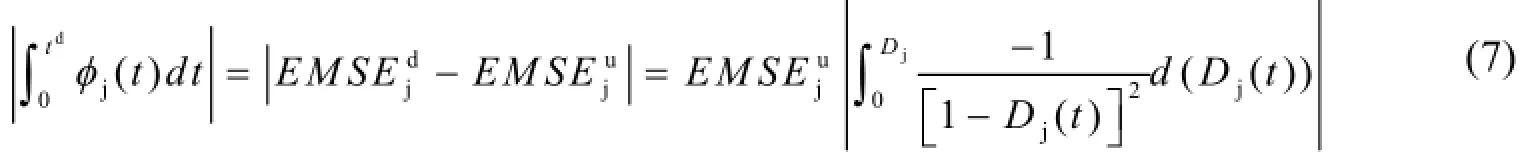
由式（7）可得到单元j在td时刻损伤状态下的损伤变量为：

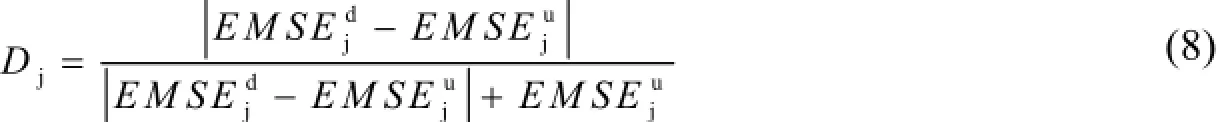
根据式（8）可计算出各单元损伤变量的具体数值，通过对比各单元损伤变量值的大小即可进行损伤定位，并在一定程度上判断单元的损伤程度［7］。

2　有限元分析

以简支工字钢梁为数值模拟的研究对象，材料为10号工字钢，其具体参数为：梁长l=2800 mm，截面面积A=9.589×10-4m2，惯性矩Ix=1.701×10-6m4，材料弹性模量E=2.06×1011N/M2，密度ρ=7850 kg/m3。将上述梁沿跨度以100 mm的单位长度进行划分，划分为28个单元。其有限元模型及节点编号如图1所示。

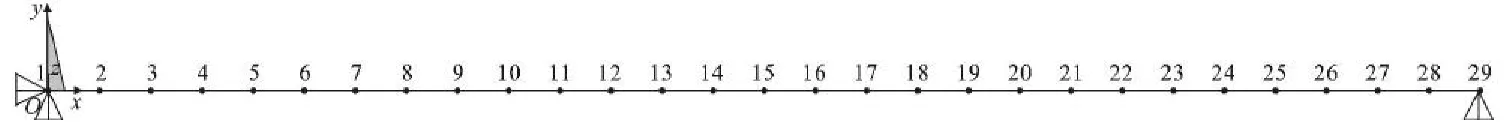
图1　梁的有限元模型及节点编号示意图Fig.1 Schematic diagram of finite element model and joint numbers of beams

本文为模拟简支钢梁的损伤的情况，采用降低单元弹性模量的方式予以实现［8］。应用ANSYS对损伤前及处于各损伤状态的简支梁分别进行模态分析，并提取其模态参数，然后将提取到的模态振型带入MATLAB自编程序计算各单元相应的损伤变量。

分别对单位置损伤和两位置损伤进行分析，分为如下四个工况。工况1：跨中附近单元（单元14）的刚度分别降低5%、10%、20%、30%；工况2：四分点附近单元（单元21）的刚度分别降低5%、10%、20%、30%；工况3：单元14与单元21刚度分别降低25%及10%；工况4：单元14及单元21刚度均降低25%。简支梁的损伤识别结果如图2所示。

图2　简支梁损伤识别结果Fig.2 Damage identification results of simply supported beams

从图2（a），（b）可以看出：对于简支梁单元14和单元21位置的单损伤，应用模态应变能法可准确识别出损伤位置，包括较小的损伤（刚度降低5%），并且随着损伤程度不断的加大，损伤变量对应的突变值也随之增大，说明该方法可相对表征单元的损伤程度。

从图2（c），（d）可以看出：对于简支梁两位置的损伤，无论损伤程度是否相同，应用模态应变能法均可准确识别出损伤位置，并相对表征损伤程度的大小。14单元和21单元在刚度均降低25%时，两个单元的突变值分别为0.37和0.33，可见损伤变量突变值与损伤位置有关。

3　试验研究

3.1简支梁动力试验

本试验利用一根与数值研究相同参数的简支工字形钢梁［9］，顺序制作不同的损伤，形成4根不同损伤工况的梁。简支梁支座采用规格为M12的螺栓将梁下翼缘与钢支座固定，试件下翼缘外边缘到螺栓孔中心距离为15 mm。试验梁示意图如图3所示。

图3　试验梁示意图Fig.3 Schematic diagram of test beam

试验采用的仪器设备有：高弹性聚能力锤、压电式加速度传感器、INV306N-7260智能信号采集处理分析仪及多功能滤波放大器等。力锤、传感器及试验装置示意图如图4所示。

图4　力锤、传感器及试验装置示意图Fig.4 Schematic diagram of force-hammer, sensor and test installations

试验梁等间距划分为28份，设置27个测点，支座处不激振，足够的测点数量能够保证前三阶模态信息较为准确，对应的振型拟合曲线较为光滑、完备。由于试验梁支座和振型节点处的振动位移为零，故拾振点的位置不能选在支座和所要提取振型的节点处［10］，因此本试验将传感器放于6号测点处。动态测试系统示意图如图5所示。

图5　动态测试系统示意图Fig.5 Schematic diagram of dynamic test system

试验中选择在简支梁的下翼缘切割裂缝模拟梁的局部损伤，裂缝沿梁横向设置且贯穿整个下翼缘，割工具选用角向磨光机，磨片的厚度为2 mm，裂缝的宽度与磨片的厚度一致，用改变裂缝的位置和深度的方法来模拟不同的损伤工况。裂缝切割位置示意图如图6所示，具体的损伤工况设置如表1所示。

图6　裂缝切割位置示意图Fig.6 Schematic diagram of cracks cutting position

表1　试验梁损伤工况Table 1 Damage cases of test beams

对初始状态及每一损伤工况下的试验梁进行动态测试，采集到的振动信号经归一放大后传输到装有DASP软件的计算机中，通过对振动信号进行自谱以及模态两种分析，获取各损伤工况下试验梁的振动特性，进而利用试验梁损伤前后的模态参数对预设损伤进行识别。

3.2结果分析

无损伤状态下，试验梁前三阶固有频率理论值为：f1=43.18 Hz，f2=172.15 Hz，f3=385.21 Hz；动测试验得到的试验梁前三阶固有频率为：f1=47.34 Hz，f2=162.62 Hz，f3=347.68 Hz。以上误差的产生主要有下述几个原因：1）试验梁的尺寸和物理参数可能与数值分析时存在差异；2）动测过程受到测量噪声的影响；3）试验梁的支承形式不是理想的简支支承。

试验梁损伤前后的前三阶固有频率测量值如表2所示。利用试验梁损伤前后的模态振型数据，基于模态应变能法得到的识别结果如图7所示。

由表2可以看出：随着试验梁损伤数量以及损伤程度的增加，试验梁前三阶频率均出现降低。对于深度为2 mm的损伤，试验梁的频率下降较小，前三阶频率下降率最大值为0.08%；对于深度为4 mm的损伤，其频率下降较为明显，三阶频率在工况2变化最为明显，下降量达到9.72 Hz，二阶频率在工况4变化最为明显，下降量达到12.22 Hz。原因是工况2的损伤位置为梁的跨中，是三阶模态位移变化最大的位置，工况4的损伤位置为梁右端四分点处，是二阶模态位移变化最大的位置。

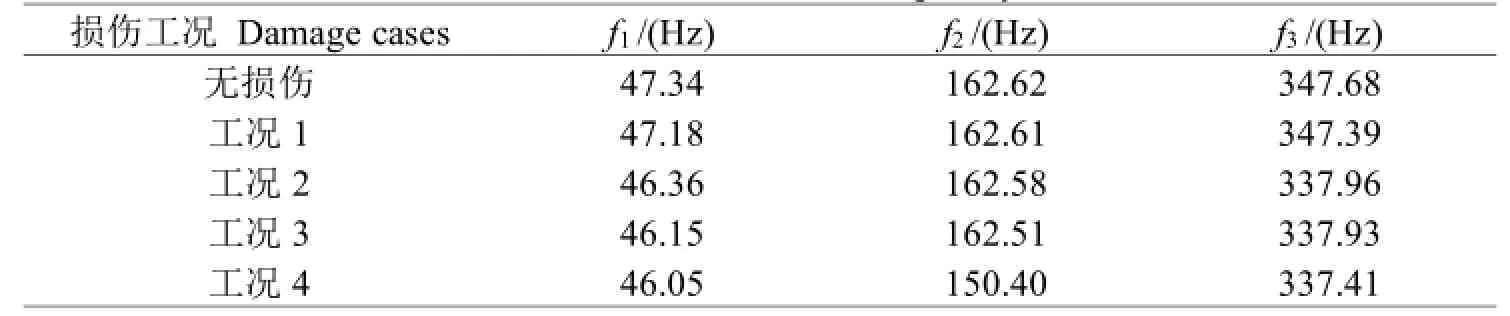
表2　试验梁固有频率测量值Table 2 Measured value of natural frequency of test beam

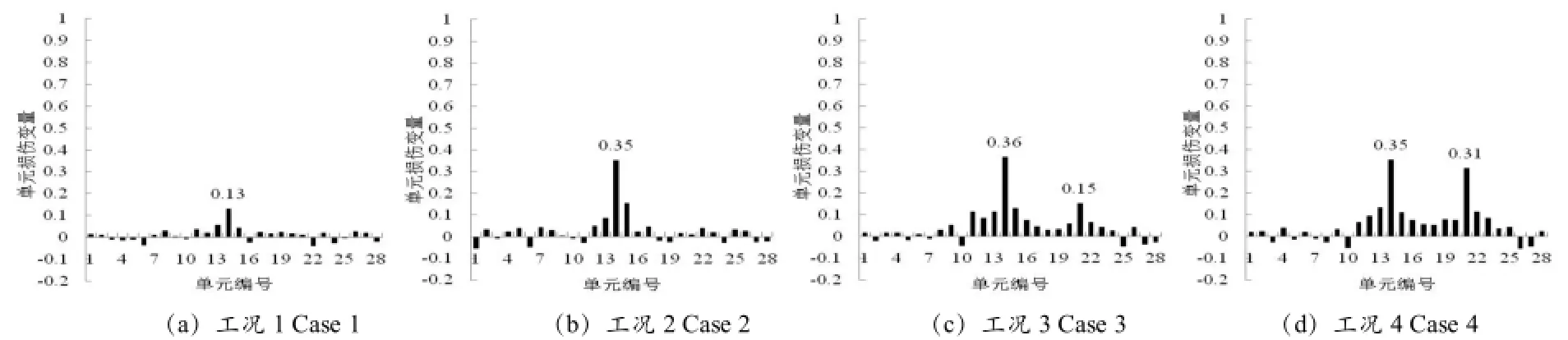
图7　试验梁损伤识别结果Fig.7 Damage identification results of test beams

从图7可看出：对于试验梁各工况下的损伤，预设损伤位置处的损伤变量值均产生了突变。1）工况1和工况2分别为在梁跨中预设2 mm和4 mm的裂缝，损伤变量突变值分别为0.13和0.35，说明随着损伤程度的增加，损伤变量突变值随之增大；2）工况3为在梁右端四分点处预设2 mm的裂缝，两个损伤位置的突变值分别为0.36和0.15，说明该方法可以识别出梁中非对称位置同时存在的两个不同程度的损伤，并可通过损伤变量突变值的大小相对表征多个损伤的损伤程度；3）工况4为在梁右端四分点处预设4 mm的裂缝，两个损伤位置的突变值分别为0.35和0.31，说明该方法可以识别出梁中非对称位置同时存在的两个相同程度的损伤；4）对于相同的损伤程度，损伤变量的计算值略有不同，这是由于裂缝的切割以及试验梁模态参数的测量过程中存在误差所导致的。

与通过固有频率变化的损伤识别相比，模态应变能法可更准确地对梁损伤位置及损伤程度识别。

4　结论

1）通过对简支梁损伤识别的数值研究得出：模态应变能法可对简支梁的损伤进行准确的识别。随着损伤程度的增大，其损伤变量突变值也逐渐增大；应用模态应变能法对简支梁的损伤进行识别时，识别结果与损伤单元在梁中所处的位置有关，若要对各损伤单元的损伤程度进行精确的定量评估，需要综合考虑损伤单元在梁中所处的位置等因素。

2）通过试验研究的方法应用固有频率变化和模态应变能法对简支梁的损伤进行识别得出：随着损伤数量以及损伤程度的增加，试验梁的前三阶频率均出现降低，各阶频率的变化量与损伤位置有关，对于深度为2 mm的损伤，试验梁前三阶频率下降率最大值为0.08%，且固有频率只能用于判别损伤的出现，不能确定具体的损伤位置；模态应变能法对于相同位置2 mm和4 mm的裂缝，损伤变量突变值分别为0.13和0.35，且随着损伤程度的增大，损伤变量突变值也逐渐增大。对于非对称位置的两处损伤，无论损伤程度是否相同，损伤位置处均出现了突变。与通过固有频率变化的损伤识别相比，识别效果具有明显优势。

参考文献

［1］Kim JT，Stubbs N. Model-uncertainty impact and damage-detection accuracy in plate girder［J］. Journal of Structural Engineering，1995，121（10）：1409-1417

［2］杨秋伟.基于振动的结构损伤识别方法研究进展［J］.振动与冲击，2007，26（10）：86-91，100，190

［3］吴波，李惠，李玉华.结构损伤分析的力学方法［J］.地震工程与工程振动，1997，17（1）：14-22

［4］余天庆，钱济成.损伤理论及其应用［M］.北京：国防工业出版社，1993

［5］张斌.基于模态应变能的钢结构损伤识别研究［D］.西安：西安建筑科技大学，2012

［6］张新亮.基于完备模态空间的两阶段结构损伤识别方案［D］.重庆：重庆大学，2007

［7］朱宏平，余璟，张俊兵.结构损伤动力检测与健康监测研究现状与展望［J］.工程力学，2011，28（2）：1-11，17

［8］郑飞，许金余.基于缩聚模态应变能与频率的结构损伤识别［J］.工程力学，2012，29（7）：117-123

［9］薛刚，李奉阁，刘海生.损伤钢筋混凝土简支梁模态频率变化规律试验研究［J］.四川建筑科学研究，2011，37（2）：46-48，54

［10］黄晓峰.脉冲锤击法中采样频率设置探讨［J］.常德师范学院学报，2003，15（2）：43-45

Study on Damage Identification for Simply Supported Steel Beam Based on the Theory of Modal Strain Energy

XUE Gang，SU Tian，WANG Chong-ge

School of Architecture and Civil Engineering/Inner Mongolia University of Science and Technology，Baotou 014010，China

Abstract：In order to solve problems that current most damage identification methods of beam structures are not accurate enough and model experiments are insufficient for verification of numerical simulation results，damage identification of simply supported I-beams was researched through numerical analysis and test based on the theory of modal strain energy. The research results showed that the modal strain energy method could identify damages inside the simply supported beam in comparison with damage identification based on natural frequency changes，modal strain energy method had obvious advantages in identification of beam damage position and degree.

Keywords：Modal strain energy；simply supported steel beam；damage identification；finite element analysis

中图法分类号：TU317

文献标识码：A

文章编号：1000-2324（2016）03-0447-05

收稿日期：2016-01-05修回日期：2016-03-25

基金项目：内蒙古自治区自然科学基金：工业厂房不良振动控制及振动疲劳寿命预测（2015MS0552）

作者简介：薛刚（1968-），男，博士，教授，主要研究方向为工程结构损伤检测. E-mail：xuegang-2008@126.com

*通讯作者：Author for correspondence. E-mail：sutian19891213@163.com