求解全局优化问题的两阶段模式搜索算法

孙莉，王传伟，潘浩

1.山东农业大学信息科学与工程学院，山东泰安2710182.山东农业大学农业资源与环境博士后科研流动站，山东泰安271018



求解全局优化问题的两阶段模式搜索算法

孙莉1，2，王传伟1，潘浩1

1.山东农业大学信息科学与工程学院，山东泰安271018
2.山东农业大学农业资源与环境博士后科研流动站，山东泰安271018

摘要：将Matlab中全局优化工具箱中的模式搜索求解器与割峰函数结合，提出一个两阶段模式搜索算法。首先通过模式搜索求解器求解包含多个极小值的优化问题，返回结果后，在当前迭代点处定义割峰函数，继而采用模式搜索求解器进一步极小化辅助函数寻找比当前结果更好的下降点。该算法简单易行，数值结果表明新算法提高了模式搜索求解器获得全局解的效率。

关键词：全局优化工具箱；模式搜索求解器；割峰函数；全局优化问题

1　引言

全局优化问题中有多个局部极小点，因此不能简单用通常意义下的局部极小化方法求解。目前Matlab全局优化工具箱中设计了5个求解器处理这类问题，包含全局搜索和多初始点求解器，遗传算法求解器，多目标遗传算法求解器，模式搜索求解器和模拟退火求解器。其中模式搜索求解器（patternsearch）的求解过程无需目标函数的梯度信息，适合于求解工程中常见的目标函数不可微甚至不连续的具体问题。另一方面，多初始点和模式搜索求解器易于并行［1，2］，使得这类算法更加适合于求解大规模的优化问题。由于至今仍没有很好的全局性判断准则，因此提高现有算法获知全局最优解的效率意义重大。

本文考虑如下界约束全局最优化问题，

经测试，模式搜索求解器在一些算例中被局部极小值所限，未能在全局搜寻更好的解。本文提出的两阶段模式搜索算法，在模式搜索终止前，于返回解处定义割峰函数，随后再次利用

论文结构如下：第二部分给出割峰函数的定义，并提出两阶段模式搜索算法，第三部分通过数值测试验证新算法的有效性。

2　两阶段模式搜索算法

2.1割峰函数

下面给出与本文算法相关的定义，文献［3］中的割峰函数定义如下，

定义1（割峰函数）

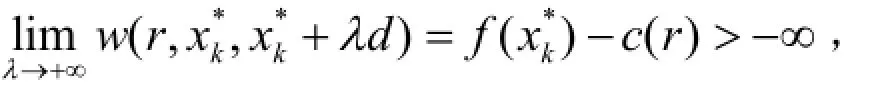
定义2（选择函数）

2.2新的割峰函数

考虑到具体应用中，迫切需要简单、易操作的全局优化算法，我们对文献［3］中的割峰函数法进行改进，将其与Matlab全局优化包中的模式搜索求解器结合起来。

本文中的割峰函数定义如下：

图1给出了与本文密切相关的三个函数：目标函数（l）、割峰函数（w）、选择函数（F）的关系。图中目标函数为，割峰函数

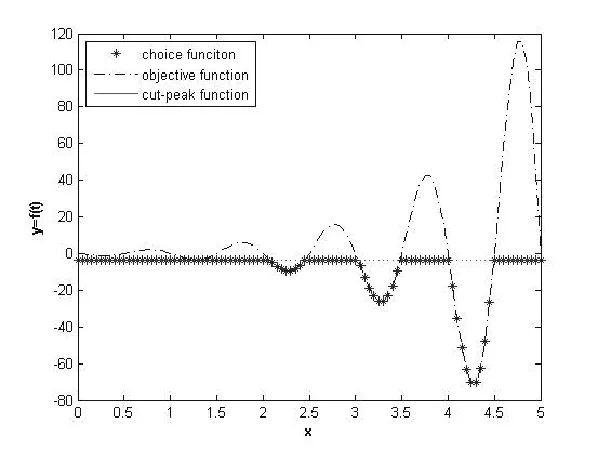
图1　选择函数、目标函数和割峰函数Fig.1 Relation of the choice function, objective function and cut peak function

2.3两阶段模式搜索算法

步0选取初始点x0，置k： =0。

步1（第一阶段）

以xk为初始点，利用模式搜索求解器获得问题（1）的局部极小点

步2（第二阶段）

3　数值测试

这一部分给出方向割峰函数算法的数值试验结果。我们引用全局优化问题中的4个经典算例进行测试，同一算例采用相同的初始点，分别通过MATLAB 2010a中的patternsearch solver（PS）以及两阶段模式搜索算法求解（TSPS）求解。

下列表格中的IT表示总体迭代次数，IF表示目标函数值的计算次数，IW表示割峰次数，FP表示最优点，FF表示最优解处的函数值。

算例1 Six-hump Camel-back Function

表1　算例1的测试结果Table 1 Numerical results of problem 1

算例2 Shubert I Function（n=2）

表2　算例2的测试结果Table 2 Numerical results of problem 2

算例3 Shubert II Function（n=2）

表3　算例3的测试结果Table 3 Numerical results of problem 3

算例4 Shubert III Function（n=2）

数值结果表明，在局部最优点处定义的割峰函数可有效判断当前点是否为全局最优解，它的引入提高了原有模式搜索求解器获知全局最优解的效率。

4　结论

本文提出的两阶段模式搜索算法，原理简单，易操作，为工程应用中的全局优化问题提供了新的有效方法。下一步我们将针对具体问题的特性，通过调整割峰函数的形式，提高优化问题的求解精度。

参考文献

［1］黄利国，孙莉，韩丛英.整体异步的并行转换算法［J］.计算机工程，2008，34（21）：54-58

［2］黄利国，韩丛英，孙莉.基于变量转换的并行优化算法［J］.计算机工程，2010，36（23）：34-35

［3］Wang YC，Fang WW，Wu TJ. A cut-peak function method for global optimization［J］. J. Comput. Appli. Math，2009，230：135-142

［4］Yang YJ，Shang YL. A new filled function method for unconstrained global optimization［J］. Appli. Math. Comput，2006，173（1）：510-512

［5］Yao Y. Dynamic tunneling algorithm for global optimization［J］. IEEE Trans. System Man Cybernet，1989，19（5）：1222-1230

［6］孙莉，贺国平，房亮.基于求解大规模界约束问题的三种有效集识别策略的比较［J］.数值计算与计算机应用，2009，30（1）：41-47

［7］张煜东，吴乐南，王水花.基于遗传算法与模式搜索的混合优化算法［J］.南京信息工程大学学报：自然科学版，2012（1）：34-39

The Method of Two Stage Pattern Search for Bound Constrained Global Optimization

SUN Li1，2，WANG Chuan-wei1，PAN Hao1

1. College of Information Science and Engineering/Shandong Agricultural University，Taian 271018，China
2. The Post-doctorate Research Station of Agricultural Resources and Environment/Shandong Agricultural University，Taian 271018，China

Abstract：We presented a two stage pattern search method，which combined the cut-peak function and the pattern search solver in Matlab. A simple cut-peak function and choice function were defined at solution returned by pattern search solver. By minimizing the choice function，a global descent of the original objective function was assured. Since the pattern search method did not require the gradient of the choice function，smoothing technique was not employed. The new algorithm was simple to implement and numerical results indicated that the new method improved the efficiency of finding the global minimization.

Keywords：Global optimization toolbox；pattern search solver；cut peak function；global optimization

中图法分类号：O221；TP312

文献标识码：A

文章编号：1000-2324（2016）03-0465-04

收稿日期：2014-02-23修回日期：2014-03-05

基金项目：国家自然科学基金资助项目（10901094，11301307）；山东省优秀中青年科学家科研奖励基金资助项目（BF2011SF024，BF2012SF025）

作者简介：孙莉（1980-），女，泰安人，副教授，博士，研究方向为最优化算法与理论. E-mail：sunlishi@hotmail.com