基于高斯模型的随机采样网络数据重构的研究
王 倩,吴宣够
基于高斯模型的随机采样网络数据重构的研究
王倩,吴宣够
摘要:现有基于压缩感知的网络数据收集需要网络中所有节点参与单个测量值收集,由于网络丢包、数据易错性、网络节能等原因导致很难满足现有压缩感知理论的要求。本文提出一种基于高斯扩散模型的随机采样网络数据重构方法,既能有效压缩待收集网络数据,又能精确恢复未采样数据。真实网络数实验结果表明该方法的有效性,同时为基于压缩感知的随机采样数据收集提供参考。
关键词:压缩感知;传感器网络;随机投影;高斯扩散模型
无线传感器网络(Wireless Sensor Network,WSN)已广泛的用于各种数据监控应用。由于受到传感器节点能量、存储能力、通信带宽等资源的限制,其大规模部署会导致系统无法长时间运行[1,2]。在数据收集的过程中,尽可能减少网络中传输的数据包数目有利于延长网络运行时间。同时,由于WSN是一种不可靠网络,网络丢包现象十分严重,从而导致收集到的数据残缺不全。故研究如何减少网络能量消耗同时保证监控数据的质量成为WSN数据收集的重点内容之一[3]。通常无线传感器网络所监控的数据具有一定的时间相关性,这为减少网内传输数据数目和利用相关性对未采样数据恢复成为可能。
压缩感知(Compressive Sensing, CS)[4,5]作为一种新的数据采样和信息获取理论,其可以有效减少网络传输的数据包数目和平衡网络能量消耗。目前,基于压缩感知的无线传感器网络数据收集已存在不少研究,如文献[6,7]提出利用高斯随机矩阵投影进行大规模WSN数据收集中,其可以减少网络中传输的数据包和平衡网络能量消耗。文献[8,9]提出稀疏随机投影网络数据收集无需网络中所有节点参与同一个测量值的收集。我们前期的研究结果表明通过时空预测和最稀疏随机投影可以进一步减少网络中传输的数据包数目和降低网络能量消耗[10,11]。现有的研究主要集中在如何使得投影矩阵变得更加稀疏和投影矩阵符合网络路由,本文旨在最稀疏投影矩阵下随机采样感知数据的恢复重构研究。
接下来,首先介绍基于压缩感知的无线数据收集,其次给出一种基于高斯扩散模型的网络数据采样和重构方法,最后通过真实的网络数据验证我们提出方法的性能。
1 基于压缩感知的无线网络数据收集
1.1压缩感知
压缩感知是对传统数据压缩理论和香农采样理论的一个突破和发展。香农采样理论认为采样频率需要大于被采样信号最高频率的两倍以上。而压缩感知理论宣称:压缩和采样可以同时进行,对可压缩信号或稀疏信号进行少量的线性投影即可获取该信号的绝大部分信息,并且具备编码简单解码复杂的特点。基于压缩感知的数据压缩过程如图1所示。

图1采用压缩感知理论对信号进行压缩
其中,x是被压缩信号,y 是压缩后信号。x可以利用稀疏表示基(正交矩阵)Ψ转化为稀疏信号s(s=Ψ-1x),稀疏信号是指包含少量的非零元素而绝大部分元素值都为零的信号。Φ表示M×N测量矩阵或投影矩阵(M≪N)。对信号的恢复过程转化为求解下面的优化问题:
(1)
目前,已存在多种对问题(1)的高效求解算法,如OMP算法[12], CoSaMP算法[13]等。Φ和Ψ满足等距离约束性质是被压缩信号可以正确恢复的前提条件。
1.2基于压缩感知的网络数据收集


图2 多跳链式压缩感知数据收集
2基于高斯扩散模型的无线网络数据重构
2.1基于压缩感知的高斯扩散模型

其中,dij为第i个采样值位置到第j个采样值位置的距离,G为高斯扩散模型矩阵。则待收集数据x可以表示为x=Gu,u为x在高斯扩散模型下的对应的参数。如果投影矩阵为最稀疏投影矩阵,即投影矩阵每一行只有一个非零值。假设最稀疏投影矩阵Φ表示如下:
其中,ri为第i个采样点随机产生的1到N之间的随机数。按如上Φ的定义可知Φ中每一行只有一个非零元素。则,基于压缩感知的收集数据可以表示为:
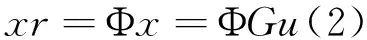
其中,xr为压缩感知的测量值向量。根据G的定义,我们可知G为实对称矩阵。则,G可以表示为G=ΨΛΨ-1,Λ为对角化矩阵,Ψ为G的特征值对应的特征向量矩阵且Ψ为标准正交基。根据以上假设和分析,方程(2)可以表示为xr=ΦGu=ΦΨΛΨ-1u=ΦΨs,即s=ΛΨ-1u。根据压缩感知理论可知其解码过程为:
(3)

2.2算法实现
根据以上高斯扩散数据恢复模型,我们很容易在分布式网络数据采样过程中实现投影矩阵Φ,即每个节点独立均匀随机的产生一个随机概率,如果该概率大于事先设定的阈值,则进行采样并上传采样数据,否则不进行数据采样。对与汇集点对整过网络数据的恢复如算法1所示。
3性能评价
3.1实验数据
为了更好的评价基于高斯扩散模型的数据重构方法,本实验选用两种真实的网络数据,它们分别为:1)Intel Lab 实验数据,其包含54个节点的室内温度数据[14];2)GreenOrbs网络数据,其包含330个节点的室外温度数据[3];3)WorldClim的一定区域的温度气象数据[15]。通过以上三个数据集来评价本文提出的高斯扩散网络数据收集性能,其中包括数据压缩性能和全局数据的恢复性能。为了评价数据恢复性能,我们采用平均信号恢复误差作为数据恢复评价标准,其定义为:
(4)
3.2压缩性能评价
由于在基于压缩感知的数据收集过程中,待收集信号的压缩性能直接决定网络中需要收集的测量值数目。待收集数据对应的稀疏信号越稀疏,所需的测量值数目越少,即M=O(klogN/K),其中M为汇集点需要收集的测量值数目,k为待收集数据对应稀疏信号的稀疏程度,N为网络中所有数据的数目[5]。下面我们通过256个GreenOrbs网络数据来验证我们提出的高斯扩散表示基具有良好的网络数据压缩功能,对比的稀疏表示基为现有基于压缩感知数据收集中常用的离散余弦变换(DCT)和小波变换(DWT)。图3(a)为网络中同一时间段内256个传感器节点的温度数据,图3(b)为在高斯扩散表示基Ψ下的系数向量s,从图3(b)中可以看出主要幅度数据集中在少数元素上,即高斯扩散表示基Ψ具有良好的数据压缩性能。图3(c)显示的为高斯扩散表示基与DCT和4层‘haar’小波变换对比实验,实验结果表面Ψ的性能介于两者之间。

图3GreenOrbs数据压缩性对比结果
3.3网络数据恢复性能对比
压缩性能评价只能说明在数据收集的过程中无需额外数目的测量值来恢复全局数据和现有通用表示基相比。除此之外,还需要验证全局网络数据的恢复精度与测量值之间的关系,能否比较准确的恢复为采样数据。图4显示的为连续6轮Intel Lab温度数据高斯扩散随机采样数据恢复结果。图4(a)中温度为0的值为未采样数据(共324个数据,随机采样200个温度数据),图4(b)为根据我们提出的方法恢复的全局数据,其误差为0.0328。实验结果表明在数据丢失严重的情况下,高斯扩散随机采样数据恢复策略能有效恢复全局数据。图5(a)显示的是WorldClim数据中某一区域9月份的平均气温包含64x64个数据,图(b),(c),(d),(e)和(f)分别为选取120,140,160,180,200个数据作为测量值,同时对应方程(4)恢复的稀疏程度K为33,35,38,53和58。实验结果表明即使只有 120个数据全局数据也能有效恢复。图6显示的是不同测量值恢复的误差对比结果。
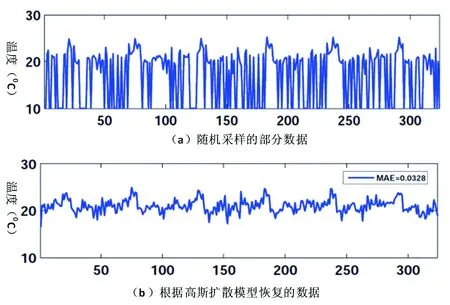
图4Intel lab实验数据恢复结果
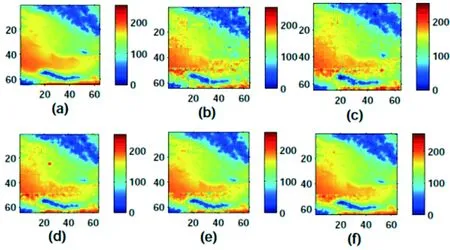
图5WorldClim气象数据恢复性能结果

图6WorldClim数据在测量值数目下的性能恢复结果
4总结
本文在分析现有基于压缩感知网络数据收集的基础上,提出一种基于高斯扩散模型的随机采样网络数据收集和重构方法。实验结果表明该方面具有良好的数据恢复功能,其可以有效应对网络丢包、数据残缺不全和减少网络数据采样,从而可以有效减少网络资源消耗和延迟无线传感器网络的运行时间。
[参考文献]
[1]Akyildiz I F, Su W, Sankarasubramaniam Y, et al. Wireless sensor networks: a survey[J]. Computer networks, 2002, 38(4): 393-422.
[2]刘云浩. 物联网导论[M].北京:科学出版社. 2011,
[3]Liu Y, He Y, Li M, et al. Does wireless sensor network scale? A measurement study on GreenOrbs[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(10): 1983-1993.
[4]李树涛, 魏丹. 压缩传感综述[J]. 自动化学报, 2009, 35(11): 1369-1377.
[5]R.G. Baraniuk. Compressive sensing. IEEE Signal Processing Magazine, 2007, 24(4):118-121.
[6]Luo C, Wu F, Sun J, et al. Compressive data gathering for large-scale wireless sensor networks[C] //Proceedings of the 15th annual international conference on Mobile computing and networking. ACM, 2009: 145-156
[7]C. Luo, F. Wu, J. Sun, and C.W. Chen. Efficient measurement generation and pervasive sparsity for compressive data gathering[J]. IEEE Transactions on Wireless Communications, 2010,9(12):3728-3738.
[8]Wang W, Garofalakis M, Ramchandran K. Distributed sparse random projections for refinable approximation[C] //Proceedings of the 6th international conference on Information processing in sensor networks. ACM, 2007: 331-339.
[9]Wu X, Liu M. In-situ soil moisture sensing: measurement scheduling and estimation using compressive sensing[C] //Proceedings of the 11th international conference on Information Processing in Sensor Networks. ACM, 2012: 1-12.
[10]Wu X, Xiong Y, Yang P, et al. Sparsest random scheduling for compressive data gathering in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(10): 5867-5877.
[11]Wu X, Yang P, Jung T, et al. Compressive sensing meets unreliable link: sparsest random scheduling for compressive data gathering in lossy WSNs[C]//Proceedings of the 15th ACM international symposium on Mobile ad hoc networking and computing. ACM, 2014: 13-22.
[12]J.A. Tropp and A.C. Gilbert. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 2007, 53(12):4655-4666.
[13]D. Needell and J.A. Tropp. Cosamp: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.
[14]Bodik P, Hong W, Guestrin C, et al. Intel lab data[J]. Online dataset, 2004. http://db.csail.mit.edu/labdata/labdata.html.
[15]Hijmans R J, Cameron S E, Parra J L, et al. Very high resolution interpolated climate surfaces for global land areas[J]. International journal of climatology, 2005, 25(15): 1965-1978.
责任编辑:王与
Random Sampling Data Gathering in Wireless Networks with Gaussian Diffusion Model
Wang Qian, Wu Xuangou
Abstract:Existing network data gathering techniques based on compressive sensing (CS) require all sensory data to be participated in each measurement gathering. Due to network packet loss, data fallibility and network energy saving, it is difficult to meet the requirements of CS theory. This paper proposes a random sampling data gathering with Gaussian diffusion model, which could compress the sensory data, and reconstruct the unsampling data accurately. With the real data experiments, the results show that our proposed scheme is useful, and at the same time provide the reference for CS-based data sampling and gathering.
Key words:compressive sensing; sensor network; random projections; Gaussian Diffusion Model.
中图分类号:TP393.02
文献标识码:A
文章编号:1673-1794(2016)02-0023-04
作者简介:王倩,安徽工业大学现代教育技术与网络管理中心教师,硕士;吴宣够,安徽工业大学计算机学院物联网工程系副教授,博士,研究方向:网络数据处理(安徽 马鞍山 243002)。
基金项目:国家自然科学基金资助项目(NO. 61402009)
收稿日期:2015-10-14

