面向电网运行的新能源出力特性指标体系研究——风电出力特性指标体系

王建学，张耀，万筱钟，张小奇（．西安交通大学电气工程学院，陕西西安　70049；．国家电网公司西北分部，陕西西安　70048）



面向电网运行的新能源出力特性指标体系研究
——风电出力特性指标体系

王建学1，张耀1，万筱钟2，张小奇2
（1．西安交通大学电气工程学院，陕西西安710049；2．国家电网公司西北分部，陕西西安710048）

摘要：由于风电出力具有明显的不确定性，依靠现有的风电特性指标，无法确定风电出力曲线的基本形状，一定程度上限制了风电特性指标在电网运行中的实际应用。引入了指标体系的时段属性概念，提出面向系统运行的风电出力特性指标体系。其中，指标“全日平均出力”表征了全天风电出力水平，指标“峰谷时段风电出力中位数差”表征了风电出力对系统调节能力的影响。指标“峰时段风电最小出力”表征了峰荷时段风电对电网运行的最小支撑，指标“谷时段风电最大出力”表征了谷荷时段风电对电网运行的最大挑战。以某地区5个风电场为例，计算了所提评价体系的各类指标，对历史风电出力曲线进行分类并形成多条典型风电出力曲线。计算结果说明了所提指标体系计算方便，物理意义直观，有助于开展系统运行的实际工作和相关研究。

关键词：风电；指标体系；峰谷时段；曲线分类

Project Supported by the National Natural Science Foundation of China（51277141）；the National High Technology Research and Development Program of China（863 Program）( 2011AA05A103）.

节能减排是世界能源发展的大趋势，而风力发电作为当前最为成熟的可持续能源利用技术，在全世界范围内得到了大力发展。伴随着大规模风电接入电网，由于风速具有随机性、间歇性等特点[1]，风力发电给电力系统规划和运行带来了众多的挑战。因此，如何应对风力发电的随机性和间歇性，一直是风电并网研究领域的研究热点[2-3]。

随着风电装机容量的不断提高和风电出力历史数据的大量积累，风电数据的整理分析工作也已经逐渐展开，但是尚未形成一套公认的、行之有效的评价指标体系。作为对比，日负荷曲线在多年前就形成了一套公认的、较成熟的评价指标体系[4]。其主要原因在于，日负荷曲线通常具有一定的典型形状，比如双峰曲线（早高峰和晚高峰）。此时通过定义一些简单的统计指标，比如日最大/最小负荷、日峰谷差/峰谷差率等等，电网运行人员可以直观地得到日负荷曲线的大致轮廓。以这些定量指标为基础，运行人员就能够安排电网运行方式，比如制定机组开机计划、配置机组调峰容量等。然而与负荷曲线不一样，风电出力曲线的形状各不相同。如果仅依据上述类似的简单指标，运行人员很难得到风电出力曲线的大致形状，也就难以根据这些指标进行合理决策，给电网日常运行工作带来了较大困难。换句话说，现有的风电指标体系对电网运行的指导意义不够明显，还需要进一步分析，建立适合电网运行的风电出力特性指标体系。

目前，已有不少研究从不同角度建立起风力发电的评价指标体系。在风电运行分析方面，运行人员经常使用风电出力均值、最值等基本统计量[5]。也有文献提出诸如风电机组分布系数[6]、风电场容量有效度[7]等综合性指标。指标“风电穿透率”[8]经常被用于反映区域电网中风电的发展规模。为了分析风电波动性特点，文献[9]提出了风电小时级功率变化等指标；文献[10]定义了尖峰电量和概率出力等指标；而文献[11]计算了风电功率容量系数，以此描述风电功率季节性及昼夜变化差异。除此之外，多个风电场出力相关性的量化指标也是近期研究热点，目前主要采用相关系数[12]和同时率[13]两类指标，也有文献提出了更复杂的统计学指标，例如频域相关矩阵[14]、互信息[15]等指标。

上述研究均各有侧重点，大部分指标都是来源于数理统计学知识。虽然这些指标均具有坚实的数学理论支撑，但是对于电网运行人员来说，往往难以直接理解这些数学指标的物理含义。例如，指标“相关系数”虽然能够客观地描述风电出力的相关性特性，但是无法直接使用到电网的日常运行工作中。更重要的是，从实际运行出发，指标最好能具有类似负荷曲线指标的直观性特征，才能方便地将这些指标直接用于指导风电并网后的电网运行。与全天96点风电出力曲线相比，电网运行更加关注某些特殊时段上的风电出力水平，例如峰荷时段和谷荷时段，这两个时段的风电出力水平对电网运行方式和调峰措施产生了较大影响。实际上在日常电网运行中，风电场运行人员和调度人员已经对风电出力曲线形成了一定的直观认识，比如“大多数时候风电具有反调峰特性”、“白天风小、晚上风大”等等。但是如何从电网运行角度，定义一些能够描述风电出力曲线特征的具体指标，依然是一项具有较高实用价值的研究工作。基于以上考虑，本文建立了一套适合电网运行的风电出力特性指标体系，直观地给出适应于电网运行的定量参数，以期能够为电网运行提供有益的参考。

1现行的风电出力特性指标体系

对于某条功率曲线（比如日负荷曲线、日风电出力曲线）来说，可以非常容易地计算出一系列评估指标，比如负荷率、最大出力等等。但是反过来，根据这一系列评估指标，是否能够直观地得到曲线形状，还需要针对具体问题进行分析。

在当前电力系统运行中，对于风电出力曲线的评估，往往直接参照日负荷特性的评价指标，分析其日最大值/最小值、日平均值、日峰谷差、日峰谷差率等等。但是与负荷曲线不同，由于风电出力主要受到自然风资源的影响，具有明显的不确定性。如果仅依靠这些简单指标，并不能确定风电出力曲线的基本形状。比如仅根据日最大值和峰谷差值，可以给出大致的负荷功率曲线，见图1（a）；而满足同样指标的风电曲线却很多，见图1（b）。

图1说明，对于风电出力曲线来说，这些常规的评估指标并不能准确地反映出风电出力特征。也就是说，风电出力曲线的一些关键信息被忽略。根据现有的评估指标体系，运行人员无法提取到能够直接指导电网运行的关键信息。

为了找出被遗漏的风电关键信息，需要分析为何这些指标可以表征负荷曲线而不能表征风电出力曲线。针对某特定地区，其负荷曲线往往具有一些长期不变的特征，比如早上10:00—12:00是早高峰时段；晚上19:00—21:00是晚高峰时段，并且达到全天最大负荷；晚上2:00—4:00是谷荷时段，出现全天最小负荷。那么当仅仅知道一些简单指标时，比如最大负荷为10 000 MW、峰谷差为4 000 MW，就能够大致推断出晚高峰时段（19:00—21:00）的最高负荷是10 000 MW，而深夜低谷时段（2:00—4:00）的最低负荷是10 000 MW-4 000 MW=6 000 MW。当确定了几个关键点位置后，再结合负荷的双峰特征，就能得到负荷曲线的大致轮廓。这给电网调度运行、方式制定等工作带来了极大方便。

图1给定部分指标的负荷曲线与风电出力曲线Fig. 1 Load curve and wind power curve with given indexes

然而与负荷曲线相比，风电出力曲线就不具有这样的典型特征。如图1（b）所示，即使获知全天风电最大出力，但是不能确定风电最大出力出现在上午、下午、晚上还是深夜。也就是说，指标“风电最大出力”对应的时段并不明确，所以难以直观得到风电曲线的大概轮廓。从以上比较可以看出，风电出力曲线与负荷曲线相比，其所缺少的关键信息就是指标对应的时段信息。下面针对指标体系的时段属性，提出一种适应电网运行的风电出力特性指标体系。

2一种新的风电出力特性指标体系

2.1风电出力指标的时段属性

从前面的叙述可知，风电出力特性指标需要考虑到指标的时段属性，才能相对准确地反映风电出力特性。对于给定的全天24点或者96点风电出力曲线，最极端的情况就是在指标体系内，给出每个时间点对应的风电出力数值，但是这样完全没有起到指标的表征意义，所以应该对所有时段进行分类。最常用的时段分类方法就是，参照负荷曲线的峰谷时段特征，将全天24 h划分为峰时段T1、平时段T2和谷时段T3。考虑到负荷曲线可能存在平峰和多峰等复杂情况，上述3个时段可以是多个时段的集合。

由于各级电网峰谷平时段划分不一样，这就需要一个划分标准。在实际操作中，可以参考各省市制定的峰谷分时电价方案，确定峰谷时段的划分方法。峰谷时段可以是多个时段的集合，例如甘肃省制定的高峰时段为8:00—11:30、15:00—16:00和18:30—22:00，低估时段为23:00—7:00，其余时段为平时段[16]。对于集中处于某地区的风电场来说，可以按照相应层级的具体峰谷电价方案，确定峰谷时段。例如甘肃酒泉地区的峰谷电价方案与甘肃省有所不同，其高峰时段为8:00—11:30、15:30—16:30和19:00—22:30[16]。但在我国风电多采纳大规模集中接入的方式，使得风电消纳主要是在省级电网或者区域级电网层面，而不是在地区电网层面。所以本文所提指标体系主要面向省级电网或者区域电网层面的风电运行管理工作。因此在确定峰谷时段上，需要参考各省制定的峰谷电价方案或者对应电网的整体负荷曲线形状。

需要特别注意的是，这种时段划分方法是依据负荷的大小而定，而不是依据风电出力的大小而定，其原因在于：

1）风电出力曲线形状经常发生较大变化，而负荷曲线具有一些长期不变的出力特征，据此进行时段划分相对稳定。

2）满足负荷需求是电力系统的首要目标，参照负荷的峰平谷时段划分方法，更容易分析风电出力对电网供需平衡的贡献。本文所采用的时段划分方法实用性较强，便于各级调度人员理解并计算。在此基础上，还可以引入更多相关理论，更好地描述风电曲线的时间相关性特征。

2.2平均值和中位数

对于常见以15 min为步长的96点风电出力曲线来说，对于全天风电出力的平均值可以用公式表示：

式中：n为数据点总数；Pt为第t时刻的风电出力数值。该公式可以方便地改写为计算某个时段的平均出力，比如对于谷时段T3的风电出力水平，就是对谷时段32个数据点取平均值即可，此时t∈T3。

采用平均值表征某个时段的风电出力水平，通常有一个隐含前提，即这种指标主要针对服从对称分布的数据集合。然而实际风电场出力统计表明，风电出力是一种偏态分布。一个极端例子如图2所示，绝大多数时刻的风电出力偏低，极少数时刻的风电出力达到额定装机容量。此时，采用中位数就比采用平均值更好。

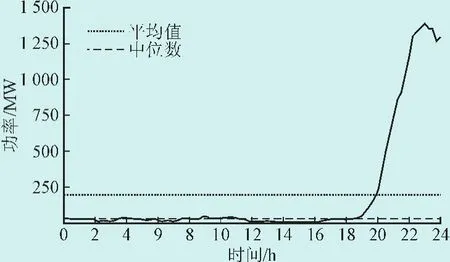
图2风电出力时间序列的平均值与中位数Fig. 2 Mean and median for wind power output time series

对于偏态的风电出力分布来说，如果采用平均值作为表征指标，“极端数据”（例如风电满额出力）会把平均数拉向自己一边，从而使得平均数出现一定程度的失真。所谓中位数就是一组数据从小到大排列后中间的那个数字，因此有一半的数据比它大，而另外一半数据比它小。与平均值相比，中位数不易受到极端数据的影响，如图2所示。因此在准确表征该时段的风电出力水平方面，中位数比平均值更具有说服力。

中位数的计算比较简单，将风电出力时间序列按照数值大小的顺序进行排列，即P′1，P′2，…，P′n则风电中位数出力可以按下式计算：

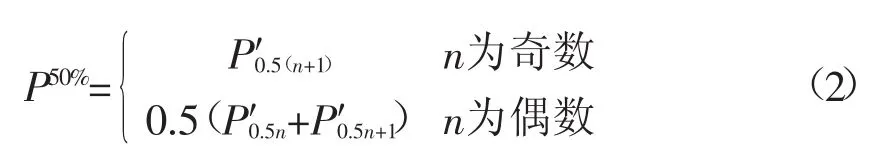
2.3风电出力特性评估指标体系

由于风电出力波动性较强，在研究风电出力特性指标时，应该特别关注2个原则：第一，该指标能够反映影响电网调度和风电场运行的主要风电出力特征；第二，该指标具有简洁明了的表达形式。满足以上2个原则的评价指标体系，能够帮助运行人员形成风电曲线的大致轮廓，直接指导电网调度和风场运行。

风电出力特性评估指标可以分为3部分：全日整体指标、分时段评价指标和单点评价指标。对于现行的风电出力特性评价指标体系来说，在全日整体指标中需要计算风电的日平均出力；在单点评价指标中需要计算风电的日最大出力和日最小出力。

基于时段属性和中位数的相关讨论，本文提出了3个全新的评估指标，即：峰时段的风电最小出力、谷时段的风电最大出力、峰谷时段风电出力中位数差。前2个指标属于单点评价指标，后一个指标属于分时段评价指标。3个新指标和已有指标“风电全日平均出力”，构成风电出力特性的基础指标体系。这里对3个新提出的评价指标进行说明。

2.3.1峰时段的风电最小出力

峰时段的风电最小出力，是指在峰荷时段中风电出力的最小值，可以用公式表示为

式中：T1为峰时段范围。如果使用传统的风电日最小出力作为单点评价指标，并不能提供太多的有效信息。若当天风电最小出力对应的时刻出现在谷荷时段内，则电网调峰更加方便，此时风力发电有利于系统运行。但是如果当天风电最小出力对应的时刻出现在峰荷时段，则电网需要安排更多常规机组容量，此时风力发电对系统支撑力度较小。从关注风电出力对电网运行影响的角度出发，风电出力特性评估指标体系应该包括指标“峰时段的风电最小出力”。

2.3.2谷时段的风电最大出力

谷时段的风电最大出力，是指在谷荷时段中风电出力的最大值，可以用公式表示为

式中：T3为谷时段范围。与前面的分析类似，如果使用传统的日最大出力作为单点评价指标，也不能提供太多的有效信息。如果当天风电最大出力对应的时刻出现在峰荷时段内，则风力发电为电网提供了更充裕的电源支撑，此时有利于系统运行。但是若当天风电最大出力对应的时刻出现在谷荷时段内，则电网调峰比较困难，可能出现弃风、弃水和启停火电机组等现象，此时不利于系统运行。从关注风电出力对电网运行影响的角度出发，风电出力特性评估指标体系应该包括指标“谷时段的风电最大出力”。

2.3.3峰谷时段风电出力中位数差

为方便阐述，这里先针对负荷出力曲线进行分析。在负荷特性分析中，“日峰谷差”是一个非常重要的指标，该指标给出了负荷曲线的全日最大变化量，从而直观地给出所需要的调峰容量，便于指导如何安排机组来满足调峰需求。通常将负荷“日峰谷差”定义为：日峰谷差=最大负荷-最小负荷。该定义隐含了两个重要事实，即最大负荷出现在峰荷时段、最小负荷出现在谷荷时段，因此日峰谷差可以按下式计算，其中，T1为峰时段范围，T3为谷时段范围：

但是针对风电出力曲线，如果直接仿照上述定义，即“风电的日峰谷差=全日最大风电出力-全日最小风电出力”，由于最大风电出力、最小风电出力可能出现在当天任意时刻，计算得到的差值并不具有类似负荷峰谷差的指导意义，因此需要对这个指标进行修改。在考虑风电的峰谷时段因素后，本文定义了一个新指标“峰谷时段风电出力中位数差”，也可以简称“峰谷中位数差”。该指标定义为：峰谷中位数差=峰时段风电出力中位数-谷时段风电出力中位数，可以按照下式计算：

式中：P50%

T1

为峰时段T1内的风电出力中位数；P50%

T3

为谷时段T3内的风电出力中位数，均可以按照式（2）计算得到。在考虑峰谷时段因素后，指标风电峰谷中位数差就具有明显的指导意义。如果该指标为正值，则说明风电处于正调峰特性，此时风电出力有利于系统运行；如果该指标为负值，则说明风电处于反调峰特性，此时风电出力不利于系统运行，并且该指标越大，说明风电反调峰特性越明显。

当然，有时为了应用方便，参照上述思路，也可以定义指标“峰谷时段风电出力均值差”，简称“峰谷均值差”，其计算公式如下：

式中：P¯T1为峰时段T1的风电出力平均值；P¯T3为谷时段T3的风电出力平均值，均可按照式（1）计算得到。在实际应用中，如果发现指标“峰谷均值差”ΔP¯和“峰谷中位数差”ΔP50%非常接近，就可以采用该指标来代替风电峰谷中位数差。然而事实上，由于风电出力波动性较强，峰/谷时段风电最大出力或平均出力往往不能代表峰/谷时段的风电可用出力。与最大值、平均值相比，中位数能够更好地表征风电在峰/谷时段的可用出力。因此，指标“峰谷时段风电出力中位数差”ΔP50%能够更加准确地反映风电对电网调峰的贡献程度。

综上所述，本文推荐的风电出力特性评估指标体系如1表所示。

表1风电出力特性评估指标体系Tab. 1 Index and evaluation of wind power output

需要指出的是，该体系内的评价指标都是从不同角度描述了风电出力特性，从而构成了基础评估指标体系。参照负荷特性指标体系，为了更准确地反映风电出力特性，还可以提出更多指标作为补充，可选指标包括：峰、平、谷时段的风电出力中位数/平均值；峰时段的风电最大出力；谷时段的风电最小出力等等。在此基础上，还可以考虑其他数理统计指标，例如负荷曲线与风功率曲线的相关系数，它能够反映两条曲线的相关性，计算公式为：

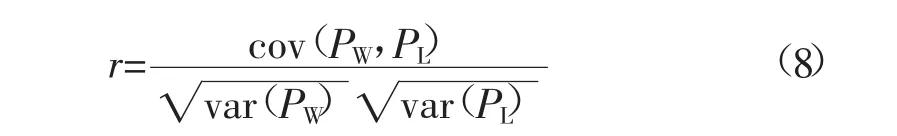
式中：PL和PW分别为负荷和风功率；cov和var分别为斜方差算子和方差算子。除此以外，一些传统的风电评估指标也具有很好的参考价值，例如风电穿透率指标，它能够反映风力发电对电网的影响。风力发电的穿透率P按照如下公式进行计算[17]：

式中：PL（t）等于某时刻的负荷大小；PW（t）为某时刻的最大能消纳的风电出力。

从电网运行角度来看，本文所推荐采用的4个指标更加精炼、更有指导意义，符合制定指标“少而精”的要求，因此更加适合省级电网层面或者区域电网层面上的风电运行管理工作。

3风电特性评估指标的应用

3.1风电特性评估指标的应用范围

本文提出的指标“全日平均出力”、“峰谷时段风电出力中位数差”、“峰时段风电最小出力”和“谷时段风电最大出力”，是一个能够广泛应用的指标体系。从应用领域来看，这些指标可以对风电历史出力曲线进行统计分析；也可以对次日风电出力预测曲线进行特征分析，从而指导次日电网调度运行、方式制定等工作；同时还可以用于构建典型风电出力曲线，有助于开展电力系统优化运行和电网远期规划等研究。

在本文提出的指标体系中，指标“全日平均出力”表征了全天风电出力水平，运行人员通过该定量指标能够直观地认识到“某日风大”或“某日风小”。指标“峰谷中位数差”表征了风电出力对电网调节能力的影响，为电网运行分析人员提供了“风电反调峰”特性的定量信息。指标“峰时段风电最小出力”表征了峰时段风电对电网运行的最小支撑，指标“谷时段风电最大出力”表征了谷时段风电对电网运行的最大挑战，这些指标都是调度人员密切关心的关键数值，因此调度人员可以从定量数据上更加直观地了解风电特性。综上所述，本文所提的指标体系可以非常方便地应用于风电出力统计、日前计划制定及电网实时调度等电网运行工作中。而在所提指标体系的基础上，如何构建典型风电出力曲线将在下文中进行阐述。

从应用时间范畴来说，本文所提的针对风电出力日曲线的指标体系，可以方便地推广到月度、季度和年度的风电出力特性指标，比如“谷时段最大出力的月度平均值”、“年最大峰谷中位数差”等等。这些指标也可以由绝对描述量转换为相对描述量，即选取基准值进行归一化操作。在所提指标体系的实际应用过程中，应当根据实际需求选择合适指标。

3.2基于评估指标的风电出力曲线分类及典型曲线

在电力系统规划中，通常需要在某些典型日下，校验所规划方案在技术上是否可行[18]，比如在制定电力远期规划时，需要分析规划水平年的某个典型大负荷日下系统的运行方式，以校验电源规划或者电网规划方案的可行性。经过多年的飞速发展，从装机容量来说，在我国北方的多个省份，风电已经成为仅次于火电的第二大电源形式。在制定电力发展规划时，不能忽略风电出力的影响。然而由于风电出力曲线形状各不相同，即使获得了多年风电历史出力数据，如何给出规划水平年的风电典型出力曲线仍然是一个难题。本文所提的评估指标可以作为一种分类标准，来解决这类难题。总体思想是先根据所提指标体系，对历史风电出力曲线进行分类，然后从各分类中提取需要的典型出力曲线，最后将典型出力曲线用于电力系统规划方案的校验工作。

在具体实现中，首先需要研究分类标准。这里以风场装机容量为容量基准值，将所提4个基础指标转换为标幺值。此时，风电出力曲线的分类指标为：①风电平均出力的标幺值C*1；②峰谷中位数差的标幺值C*2；③峰时段最小出力的标幺值C*3；④谷时段最大出力的标幺值C*4。然后设定各指标的分类阈值，就可以对风电曲线进行分类。

本文给出一种分类方法：根据风电平均出力C*1分为3类，即低出力（0～1/3）、中出力（1/3～2/3）、高出力（2/3～1）；根据峰谷中位数差C*2分为2类，即正调峰（≥0）、反调峰（＜0）；根据峰时段最小出力C*3分为2类，即低出力（0～1/2）、高出力（1/2～1）；根据谷时段最大出力C*4分为2类，即低出力（0～1/2）、高出力（1/2～1）。根据上述分类方法，理论上可以得到24类风电出力曲线。但在有些分类中，很难同时满足4个指标，比如“反调峰”、“峰时段最小出力较高”、“谷时段最大出力较低”存在逻辑冲突，在实际应用中这些分类并不存在。经过实际测算，针对本文指标的风电出力曲线分类情况如表2所示。

表2基于风电出力特性评价指标的风电曲线分类Tab. 2 Grouping wind power curve in terms of indexes

参照上述风电分类标准，就可以把大量历史风电曲线归入对应的类，然后取相近时间内该类风电曲线的平均值作为该类的典型风电出力曲线。在电力规划中，如果需要校验冬季典型日下规划方案的技术可行性，应当根据该地区冬季风电出力的基本特征，从表2中选取对应的分类。例如通常该地区冬季大风日较多，并且风电具有反调峰特性，因此就可以选取类G9和类G10作为典型风电出力曲线，进行冬季典型日校验。需要补充说明的是，典型风电出力曲线不仅可以用于电力系统远期规划，还可以用于电力系统优化运行等其他研究和计算中。

4算例分析

4.1评估指标的计算结果

这里选取某地区的、地理位置相互临近的5个大型风电场WF1（99.7 MW）、WF2（176 MW）、WF3（99.7 MW）、WF4（100.5 MW）和WF5（100.2 MW），数据时间跨度为2010—2012共3年，数据采样周期为1 h。以风电场WF1为例，图3给出了2012年冬季某典型日（1月15日）的风电场WF1实际出力曲线，图4给出了2012年夏季某典型日（7月15日）的风电场WF1实际出力曲线，并用虚线分割了全天峰谷平时段。

图3冬季1月15日的风电场WF1出力曲线Fig. 3 Wind power curve in winter at wind farm 1#on January 15，2012

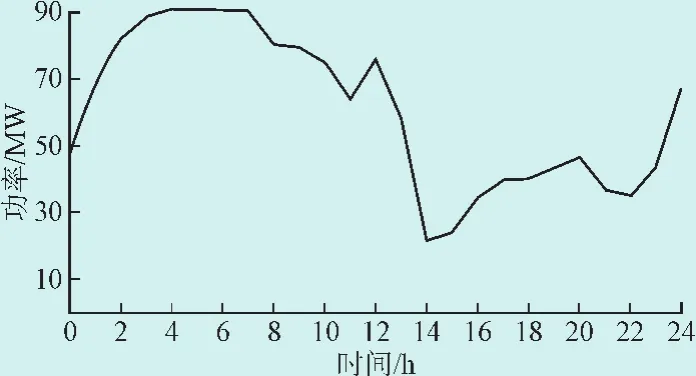
图4夏季7月15日的风电场WF1出力曲线Fig. 4 Wind power curve related in summer at wind farm 1#on July 15，2012

根据本文所提方法，表3给出了各风电场在冬季典型日（1月15日）的风电出力特性评价指标，表4给出了各风电场在夏季典型日（7月15日）的风电出力特性评价指标。

从表3中可以看出，由于风电场大致处于相同风力带上，因此计算得到的风电特性指标非常接近。在所选择的冬季典型日（1月15日）中，所有风电场出力特性类似，即风电平均出力属于中等水平、反调峰、峰段最小出力较低、谷段最大出力较高（与表2中的分类G5相对应）。尤其是风电场的峰时段最小出力较低，风电反调峰特征非常明显。从表4中也可以看出与上述相似的计算结果。

表3冬季典型日的风电出力特性指标Tab. 3 Results of wind power curve indices in winter MW

表4夏季典型日的风电出力特性指标Tab. 4 Results of wind power indexes in summer MW

最小出力最大出力

60.42-24.4335.2991.23 WF1113.17-46.6472.51160.69 WF258.03-22.3327.0288.03 WF354.67-25.2332.2687.53 WF455.71-21.4435.4787.88 WF5

对照图3和表3、图4和表4可看出，根据本文所提的指标体系及分类方法，基本上能够从指标计算结果中反推得到风电出力曲线的大致轮廓。这种逆推过程能给予运行规划人员非常直观的认识。

相对于单个风电场，电网运行更加关注风电基地或风电场群的出力特性。风电场WF1、WF2、WF3、WF4和WF5地理位置相互临近，大致处于相同风力带上，可以构成一个风电场群。表5给出了此风电场群在冬季典型日（1月15日）的风电出力特性评价指标。

表5冬季典型日的风电场群特性指标Tab. 5 Results of wind farms curve indexes in winter MW

由于各风电场地理位置相互靠近，因此计算得到的风电特性指标非常接近。因此可以认为风电场WF1、WF2、WF3、WF4和WF5具有强相关性。从表5中可以看出，这种强相关性将导致风电场群出力的波动性增强。

需要指出，这里计算的数据采样周期既可以选择1 h，也可以选择15 min，这主要取决于风电场提供的数据采样率和电网实际调度的需要。而这两个采样周期得到的指标差距并不大，限于篇幅，这里不再给出具体分析。

4.2评估指标的统计分析

本部分针对本文新引入的“峰谷时段风电出力中位数差”、“峰时段风电最小出力”和“谷时段风电最大出力”指标的统计特性规律进行分析。该统计规律建立在计算2010—2012年风电场WF1每日评估指标的基础上，然后做出了3种评估指标的统计直方图，如图5—图7所示。

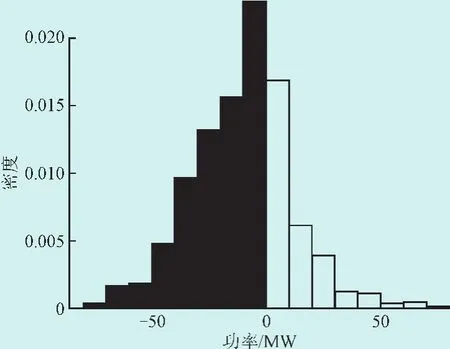
图5风电场WF1峰谷时段出力中位数差的统计直方图Fig. 5 Histogram of median difference between the peakand valley period at wind farm 1#

图6风电场WF1峰时段最小出力的统计直方图Fig. 6 Histogram of the minimum output during the peak period at wind farm 1#

图5中的“峰谷时段风电出力中位数差”统计直方图呈现出“窄而高”并且“左偏”的形状，该直方图偏向于零点的左侧意味着：峰谷时段出力中位数差小于零，即峰时段出力中位数小于谷时段出力中位数。这说明风电场WF1并网后普遍出现了“反调峰”现象，不利于电网安全运行。因此在制定备用计划、机组组合方案时，需结合该指标下的统计结果。

图6中的统计直方图“左偏”现象较为严重，说明风电场WF1在峰时段最小出力较小，不利于系统调峰运行，电网需要安排更多常规机组容量。图7中统计直方图呈现“右偏”形状，其中风电场WF1出力在80～100 MW的概率较高，这也不利于系统调峰运行，可能出现弃风、弃水和启停火电机组等现象。图6和图7针对所提指标的统计直方图，清晰说明了风电场WF1主要呈现了“反调峰”形态。

图7风电场WF1谷时段最大出力的统计直方图Fig. 7 Histogram of the maximum output during thevalley period at wind farm 1#

4.3风电分类和典型曲线

在计算得到本文所提出的4个指标后，按照表2中列出的分类标准，对从2010—2012年的5个风电场WF1-WF5全部风电日出力曲线（共计1 096条风电曲线）进行分类，分类结果如表6所示。

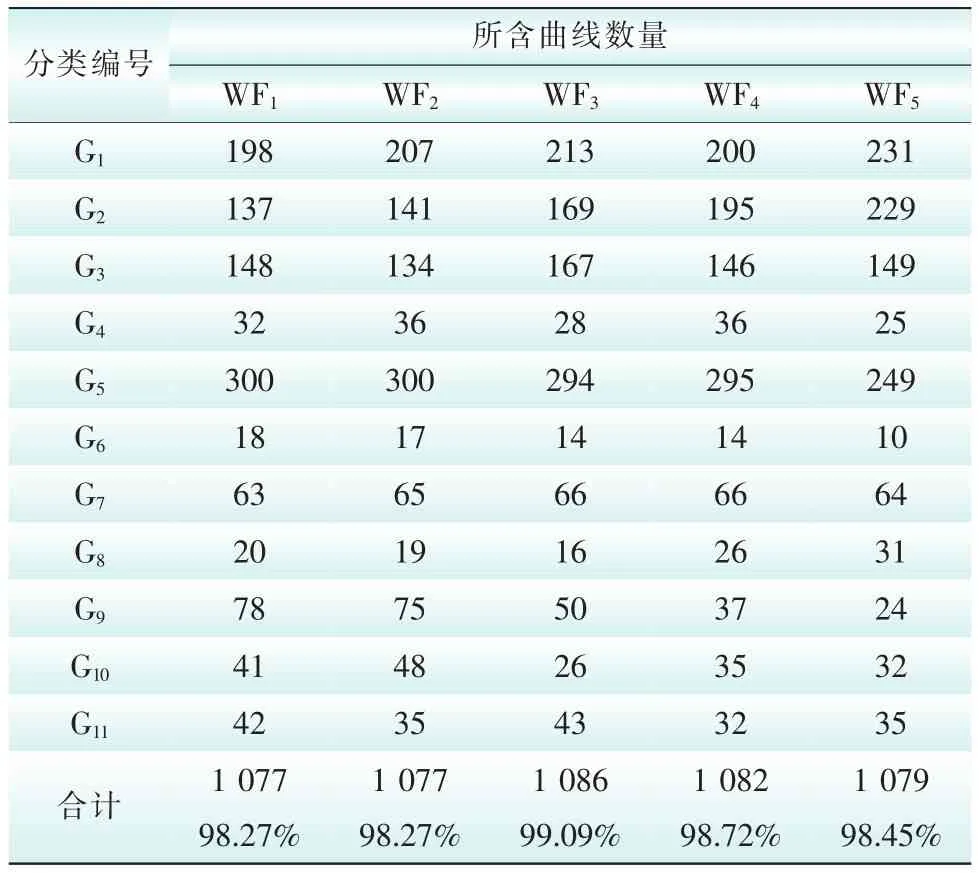
表6历史风电出力曲线的分类结果Tab. 6 Results of grouping historical wind power curves

从表6可以看出，本文提出的描述风电出力特征的11个分类，几乎全部包含了现实中风电出力可能出现的所有形状，5个风电场的总体覆盖率达到了98.56%，因此所提分类标准具有高表征性和高覆盖率。其中G1和G5类出现几率最大，说明该区域风电场整体出力不大，且多具有反调峰特性。

在开展电力系统规划方案的校验工作时，可以从各分类中提取所需要的典型风电出力曲线，即取相近时段内该类风电出力曲线的平均值作为该类的典型风电出力曲线。针对风电场WF1，图8、图9和图10分别给出了低出力分类G1、中出力分类G5和高出力分类G9对应的典型风电出力曲线。

图8分类G1对应的典型风电曲线Fig. 8 Typical wind power curve related with G1

图9分类G5对应的典型风电曲线Fig. 9 Typical wind power curve related with G5

图10分类G9对应的典型风电曲线Fig. 10 Typical wind power curve related with G9

可以看到，该风电场WF1具有低出力、中出力和高出力3条典型风电曲线。本文还采用“均方根误差RMSE”评估了典型出力曲线和实际风电出力曲线的偏差。以分类G5为例，RMSE计算公式见式（10）。其中P¯G5i（i=1，2，…，24），表示分类G5的典型风电出力曲线，如图9所示。Pki（i=1，2，…，24）表示属于分类G5的第k条实际风电出力曲线，如图3和图4所示。PN表示风电场装机容量。

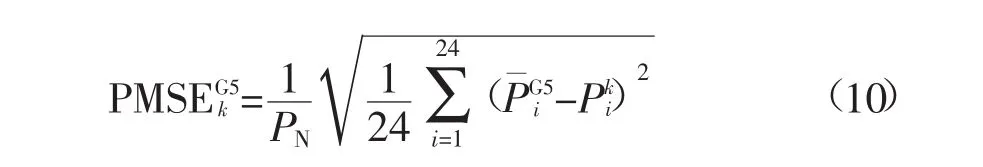
最后针对每个分类编号，分别统计RMSE的平均值、最小最大值和RMSE≥15%、RMSE≥20%的频率。表7给出了风电场WF1各分类编号对应的RMSE各项统计指标。从表7中可以看到，大多数分类对应的RMSE平均值都小于20%，所有分类的RMSE平均值为15.48%，这比实际运行中对日前风电预测误差要求的RMSE≤20%要低，证实了本方法所得到的典型风电出力曲线的准确性。

表7典型出力曲线与实际出力曲线的RMSE结果Tab. 7 RMSE of typical and actual wind power curve

频率

频率

10.12%4.15%27.18%95.96%88.89% G 1 16.01%6.27%35.29%79.56%46.72% G 2 13.45%3.70%33.07%87.16%76.35% G 3 19.00%7.16%43.74%75.00%28.12% G 4 17.93%7.68%50.61%72.33%28.33% G 5 15.81%9.37%24.73%83.33% G 6 50.00% 20.64%10.16%36.95%47.62%17.46% G 7 20.38%14.52%35.47%55.00%10.00% G 8 12.59%4.74%21.29%97.44%70.51% G 9 11.03%4.64%21.03%95.12%90.24% G 10 13.31%4.38%28.67%80.95%73.81% G 11均值15. 48%6.98%32.55%79.04%52.77%

通过以上分析可以看出，按照本文所提指标和对应的分类方法，所得到的各分类风电典型出力曲线能够准确表征风电运行的典型特征，这给实际运行和研究都带来了方便。

5　结语

本文针对风电出力特性，结合电网运行的需求，提出了一个新的风电出力特性基础指标体系，包括“全日平均出力”、“峰谷时段风电出力中位数差”、“峰时段风电最小出力”和“谷时段风电最大出力”。

本文所提的指标体系抓住了风力发电对电网运行的主要影响因素，并且定义简洁明了，便于为电网运行人员提供直观信息。所提指标体系还可以用于形成各类典型风电出力曲线，这些典型曲线与实际出力曲线之间的偏差较小。本文所提指标，已在实际系统新能源运行分析中得到应用，说明该指标体系适应性好、具有广泛的应用前景。

参考文献

[1]颜拥，文福拴，杨首晖，等.考虑风电出力波动性的发电调度[J].电力系统自动化，2010，34（6）：79-88. YAN Yong，WEN Fushuan，YANG Shouhui，et al. Generation scheduling with fluctuating wind power[J]. Automation of Electric Power Systems，2010，34（6）: 79-88（in Chinese）.

[2]孙川永，魏磊，贾宏刚，等.新能源开发中风电、光伏理论装机比例的探讨[J].电网与清洁能源，2014，30（6）：24-27. SUN Chuanyong，WEI Lei，JIA Honggang，et al. Discussions on the theoretical installed proportion of wind power and photovoltaic power in new energy development[J]. Power System and Clean Energy，2014，30（6）: 24-27 （in Chinese）.

[3]雷亚洲.与风电并网相关的研究课题[J].电力系统自动化，2003，27（8）：84-89. LEI Yazhou. Studies on wind farm integration into power system[J]. Automation of Electric Power Systems，2003，27（8）: 84-89（in Chinese）.

[4]赵希正.中国电力负荷特性分析与预测[M].北京：中国电力出版社，2002.

[5] HANNELE H. Hourly wind power variations in the nordic countries[J]. Wind Energy，2005（8）：173-195.

[6]申洪，王伟胜.一种评价风电场运行情况的新方法[J].中国电机工程学报，2003，23（9）：90-93. SHEN Hong，WANG Weisheng. A new method for evaluating operation of wind power plant[J]. Proceedings of the CSEE，2003，23（9）: 90-93（in Chinese）.

[7]许郁，朱永强.并网风电场发电可靠性的新的评价指标[J].电气技术，2010（6）：9-12. XU Yu，ZHU Yongqiang. New reliability indices of gridconnected wind farms[J]. Electrical Engineering，2010（6）: 9-12（in Chinese）.

[8] WEI Li，GéZA JOóS. Performance comparison of aggregated and distributed energy storage systems in a wind farm for wind power fluctuation suppression[C]// Power Engineering Society General Meeting. Tampa，USA：IEEE，2007：5-10.

[9] HOLTTINEN H. Impact of hourly wind power variations on the system operation in the nordic countries[J]. Wind Energy，2005（8）：197-218.

[10]肖创英，汪宁渤，陟晶，等.甘肃酒泉风电出力特性分析[J].电力系统自动化，2010，34（17）：64-67. XIAO Chuangying，WANG Ningbo，ZHI Jing，et al. Power characteristics of Jiuquan wind power base[J]. Automation of Electric Power Systems，2010，34（17）: 64-67 （in Chinese）.

[11]周天睿，王旭，张谦，等.大规模风电对江苏电网规划影响的实证分析[J].中国电力，2010，43（2）：11-15. ZHOU Tianrui，WANG Xu，ZHANG Qian，et al. Empirical research on impact of large-scale wind power on Jiangsu power system planning[J]. Electric Power，2010，43（2）: 11-15（in Chinese）.

[12]于大洋，韩学山，梁军，等.基于NASA地球观测数据库的区域风电功率波动特性分析[J].电力系统自动化，2011，35（5）：77-80. YU Dayang，HAN Xueshan，LIANG Jun，et al. Study on the profiling of China’s regional wind power fluctuation using GEOS-5 data assimilation system of national aeronautics and space administration of america[J]. Automation of Electric Power Systems，2011，35（5）: 77-80（in Chinese）. [13]崔杨，穆钢，刘玉，等.风电功率波动的时空分布特性[J].电网技术，2011，35（2）：110-114. CUI Yang，MU Gang，LIU Yu，et al. Spatiotemporal distribution characteristic of wind power fluctuation[J]. Power System Technology，2011，35（2）: 110-114（in Chinese）.

[14] SøRENSENP，CUTULULISNA，VIGUERAS-RODRíGUEZ A，et al. Power fluctuations from large wind farms[J]. IEEE Transactions on Power Systems，2007，22（3）：958-965.

[15] BESSA R J，MIRANDA V，GAMA J. Entropy and correntropy against minimum square error in offline and online three-day ahead wind power forecasting[J]. IEEE Transactions on Power Systems，2009，24（5）：1657 -1666.

[16]甘肃省发展和改革委员会.甘肃省电网销售电价说明[S].兰州:甘肃省发展和改革委员会，2014.

[17]李剑楠，乔颖，鲁宗相，等.多时空尺度风电统计特性评价指标体系及其应用[J].中国电机工程学报，2013，33（13）：53-61. LI Jiannan，QIAO Ying，LU Zongxiang，et al. An evaluation index system for wind power statistical characteristics in multiple spatial and temporal scales and its application[J]. Proceedings of the CSEE，2013，33（13）: 53-61 （in Chinese）.

[18]王锡凡.电力系统优化规划[M].北京：水利电力出版社，1990.

王建学（1976—），男，博士，副教授，主要研究方向为新能源并网运行、微电网经济运行、电力系统检修和电力市场；

（编辑冯露）

张耀（1988—），男，博士研究生，主要研究方向为新能源概率预测和电力系统随机优化理论；

万筱钟（1974—），男，硕士，从事新能源运行和管理工作，主要研究方向为新能源电力系统运行分析和管理；

张小奇（1982—），男，硕士，主要研究方向为新能源电力系统运行分析。

（编辑黄晶）

An Operation-Oriented Evaluation Index System for Renewable Power Output Characteristics: Wind Power Output Characteristics

WANG Jianxue1，ZHANG Yao1，WAN Xiaozhong2，ZHANG Xiaoqi2
（1. School of Electrical Engineering，Xi’an Jiaotong University，Xi’an 710049，Shaanxi，China；2. Northwest China Grid Company Limited，Xi’an 710048，Shaanxi，China）

ABSTRACT：Due to the obvious uncertainty of wind power，the exact information about the shape of wind power output curve couldn't be gotten，if relying on the current wind power evaluation indexes. This drawback limits，to some extent，the sufficient application of wind power evaluation indexes in practical power grid operation. This paper introduces the concept of time dependence and proposes an evaluation index system for wind power output，which could be useful for the integration of wind power. The index“averaged wind power output per day”is used to describe the level of wind power output. The index “distinction of wind power median output between peak and valley load period”is applied to quantitatively analyze the impact of wind power output on peaking service. The index “minimum wind power output in peak load period”is related to the minimum support for power system operation. The index “maximum wind power output in valley load period”is related to the maximum challenge to power system operation. Based on calculation of typical indexes for five different wind farms，the paper explains the calculated index and application in the curve classification. The results show that the proposed index has intuitive physical meaning，and helps to carry out practical work and related research in power system operation.

KEY WORDS：wind power；index system；peak-valley time period；curve classification

作者简介：

收稿日期：2015-01-26。

基金项目：国家自然科学基金项目（51277141）；国家高技术研究发展计划（863计划）项目（2011AA05A103）。

文章编号：1674- 3814（2016）02- 0042- 10

中图分类号：TM714

文献标志码：A