基于弹性波动力学的检波器-介质耦合系统研究
陈高翔,田 钢
(浙江大学地球科学学院,浙江杭州310027)
基于弹性波动力学的检波器-介质耦合系统研究
陈高翔,田钢
(浙江大学地球科学学院,浙江杭州310027)
摘要:检波器与介质之间的耦合作用是影响地震记录质量的关键因素。基于弹性波动力学理论,开展了检波器-介质耦合问题研究,构建了耦合系统模型。通过弹性波动力学理论模型与传统振动力学理论模型对比,揭示了介质、检波器条件对耦合响应的影响以及不同理论模型的差异,提出将波动模型与振动模型数据进行融合的方法。通过融合数据与实际地震数据对比,探讨了结合波动理论与振动理论解决实际耦合问题的可行性。
关键词:检波器;耦合系统;弹性波动力学理论;振动力学理论;格林函数
工作状态下,检波器与周围介质相互作用,将来自地下目标体的地震信号转换为电信号输出。作为接收与记录地震信号的传感器,检波器在地震数据采集中起到重要作用。其中,检波器尾锥与周围介质的耦合作用最为关键,在一定程度上,可将其视为特定的滤波器,通过压制或放大不同频段内的地震信号,对地震数据的品质产生重要影响。因此,开展检波器-介质耦合系统的研究,对于还原真实的地震信号,拓宽地震频带,实现高精度地震勘探具有重要意义。
关于检波器的耦合问题,国内外学者在理论与实验方面开展了大量的研究工作[1-8]。KROHN[9]经实验发现,增加配重或增加尾锥长度能提升检波器谐振频率。徐锦玺等[10]认为,适当增加检波器尾锥长度能拓宽地震信号带宽,提高检波器接收有效信号的能力。徐淑合等[11]、石战结等[12]分别针对沙漠地区地表条件设计多种尾锥结构,优化检波器与介质的耦合性能。理论研究方面,地球物理界内主流是应用振动力学理论分析耦合系统,如刘志田等[13]提出检波器耦合系统的二自由度模型,石战结等[14-15]结合灰岩作业地区的介质条件构建三自由度耦合系统。但是理论证明振动力学模型在模拟高泊松比介质条件时存在局限性,因此RADEMAKERS等[16]与DRIJKONINGEN等[17]提出以弹性波动力学理论为基础,结合互易定理解决耦合问题。该方法考虑了弹性波在耦合区域中的转换,避免了振动力学理论由于过度简化模型而忽略高频耦合响应的弊端,能真实反映系统的耦合响应。
本文在RADEMAKERS与DRIJKONINGEN等研究基础上提出基于弹性波动力学理论的检波器-介质耦合模型,研究以泊松比、横波速度、尾锥长度及半径为代表的介质与检波器条件对耦合响应的影响,结合振动力学耦合模型,探讨了实现两种理论模型优势互补的可行性。
1检波器-介质耦合系统波动力学理论
1.1耦合系数
假设在均匀介质中,地面某点处存在的振动信号为fgrd,插置检波器后检波器机芯所接收到的振动信号为fgeo。从系统角度考虑,前者可以视作输入信号,后者可以视作经过检波器-介质耦合系统作用后形成的输出信号。因此,可以定义耦合系数C(ω),用以描述耦合系统。若vgrd(ω)表示地面某点原始速度信息,vgeo(ω)表示检波器尾锥在vgrd(ω)作用下产生的运动情况,则有:
(1)
若需考虑3个方向上的分量,则耦合系数可以表示为:
(2)
式中:i,j分别表示三维直角坐标系中的方向分量;ω表示角频率。本文主要研究检波器-介质耦合系统在垂直分量上的耦合响应特性,即C33(ω)。
1.2速度场分解
在理想条件下,震源激发的地震波传播至地表时,表层介质中的地震波场可以视为原始波场vini(ω);在地表某点插置检波器后,由于检波器与介质的弹性差异,在原始波场影响下会产生散射波场,其存在于检波器附近的介质中,记为散射速度场vscat(ω)。原始波场与散射波场叠加形成检波器-介质耦合系统的总波场vtotal(ω)。该耦合系统的耦合系数C(ω)可表示为:
(3)
1.3弹性波动力学理论基础
以下根据耦合系数定义构建理论模型。首先考虑描述弹性介质中质点运动状态的质点运动平衡方程[18]:
(4)
(5)
结合格林函数与自由弹性体空间中点震源激发波场的分布状态[19](即原始波场),速度场及应力场可表示为:
(6)
(7)
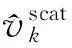
(8)
式中:Dscat表示柱状散射体模型表面区域。
(9)

图1 检波器-介质耦合系统物理模型
将Dscat拆分为柱体模型顶表面、侧表面以及底表面区域Dtop,Dside和Dbot,再结合质点的运动平衡方程,可以将(9)式转换为:
(10)
式中:h1和h2分别表示水平面至柱体模型顶部和底部的高度差,ρgeo表示检波器尾锥的密度。
结合公式(3),可以得到检波器-介质耦合系统的响应方程[17],即耦合系数C33(ω)的表达式:
(11)
2数值模拟
2.1不同介质条件下的耦合响应
土壤介质条件是影响耦合效果的主要因素,本文选取粘土、砂土、砂岩及灰岩共四种不同土壤介质作为输入,考察检波器-介质耦合系统的耦合响应差异。检波器参数为:尾锥长度0.1m,半径0.005m,质量0.4kg。
4种土壤介质的具体参数见表1,前两者代表疏松、低速介质(以下称为疏松介质),后两者代表密实、高速介质(以下称为固结介质)。

表1 不同介质的物性参数
图2显示了不同介质条件下检波器-介质耦合系统响应数值模拟结果。粘土介质峰值为203Hz;砂土介质峰值为250Hz;而固结的砂岩和灰岩峰值出现在390~400Hz内,分别为396Hz及392Hz,二者峰值较为接近。可见疏松介质的耦合系统响应峰值低于固结介质。此数值模拟结果符合实际的经验认知。
图3为不同介质条件下速度及泊松比对耦合响应的影响。图3a表示疏松介质条件,蓝色实线代表横波速度151m/s,泊松比为0.45的介质,相对振幅峰值位于203Hz;绿色实线代表横波速度171m/s,泊松比为0.44的介质,相对振幅峰值位于292Hz;红色实线代表横波速度191m/s,泊松比为0.43的介质,相对振幅峰值位于323Hz。图3b 表示固结介质条件,蓝色实线代表横波速度385m/s,泊松比为0.24的介质,相对振幅峰值位于395Hz;绿色实线代表横波速度405m/s,泊松比为0.23的介质,相对振幅峰值位于389Hz;红色实线代表横波速度425m/s,泊松比为0.22的介质,相对振幅峰值位于386Hz。对比可见,速度增加及泊松比降低所代表的介质固结程度的提升,都会引起耦合系统响应的变化,区别在于疏松介质的变化幅度较固结介质更为显著,即疏松介质条件下的耦合系统对于介质条件的变化更敏感。

图2 不同介质条件下检波器-介质耦合系统振幅响应曲线
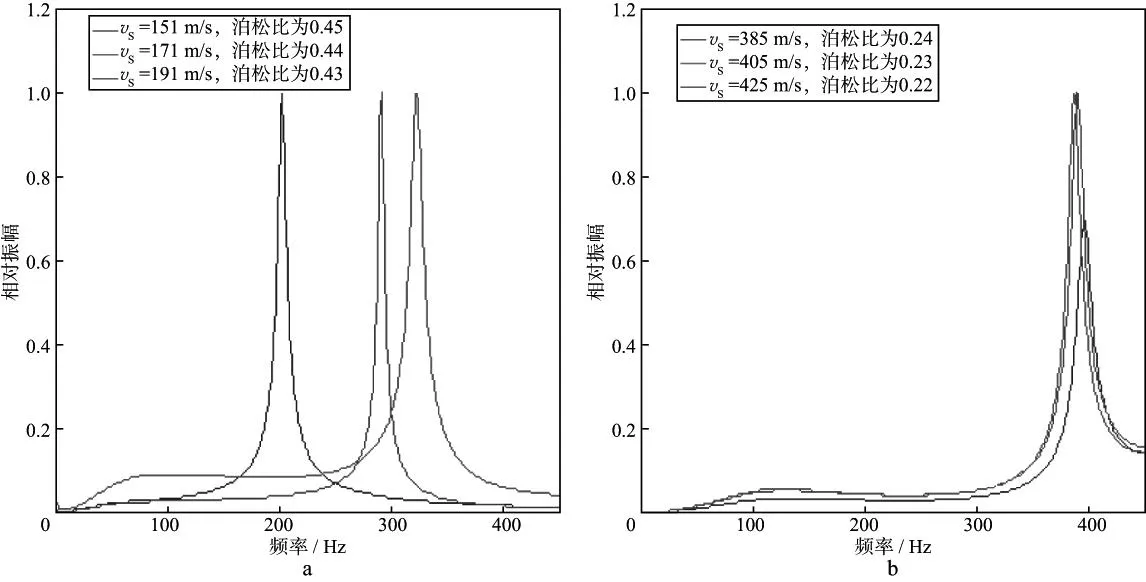
图3 不同介质条件下速度及泊松比对耦合响应的影响a 疏松介质条件; b 固结介质条件
2.2不同检波器条件下的耦合响应
检波器尾锥的物理特性是影响耦合效果的另一个关键因素,其中尾锥长度及半径的影响最为突出。
图4为疏松及固结介质条件下3种不同尾锥长度的检波器耦合响应曲线,蓝色、绿色、红色实线分别表示尾锥长度为0.11,0.10,0.09m的耦合响应。疏松介质中3种检波器条件的响应峰值分别位于203,205,206Hz处(图4a);固结介质中3种检波器条件的响应峰值分别位于402,404,405Hz处(图4b)。图5为疏松及固结介质条件下3种不同尾锥半径的检波器耦合响应曲线,蓝色、绿色、红色实线分别代表尾锥半径为0.006,0.005,0.004m的耦合响应。疏松介质条件下,3种尾锥半径条件的相对振幅峰值分别位于227,203,198Hz处,呈峰值频率随半径减小向低频移动的趋势(图5a);固结条件下三者峰值分别在315,385,395Hz处,呈峰值频率随半径减小向高频移动的趋势(图5b)。

图4 不同介质条件下不同尾锥长度的检波器耦合响应曲线a 疏松介质条件; b 固结介质条件

图5 不同介质条件下不同尾锥半径的检波器耦合响应曲线a 疏松介质条件; b 固结介质条件
由图4和图5可见,不同尾锥长度造成的响应峰值频率差异较小,说明尾锥长度的因素对于耦合效果影响有限;不同尾锥半径引起的响应峰值差异较大,且在特定介质条件下呈不同分布趋势,说明尾锥半径差异对于耦合效果具有较大影响。
2.3弹性波动力学与振动力学模型对比
考虑到构建振动力学模型是目前解决耦合问题的主流观点,因此有必要将弹性波动力学模型与振动力学模型进行对比。
振动力学在理论上假设地表介质具有弹性特征,不具有质量与惯性,而刚性尾锥具有质量与惯性,但不表现弹性性质。据此,振动力学主张将检波器-介质耦合系统简化为双自由度振动系统模型[15,21],其表述如公式(12)所示:
H(f)=
(12)
式中:f为信号频率,fc与ηc分别表示尾锥耦合振动系统的自然频率与阻尼系数,fg与ηg则表示谐振耦合振动系统的自然频率与阻尼系数。
设置疏松和固结两种介质条件,疏松介质横波速度为151m/s,泊松比为0.45,固结介质横波速度为300m/s,泊松比为0.27;同时设定检波器尾锥长度为0.1m,半径为0.005m,质量为0.4kg。图6为两种介质条件下弹性波动力学模型与振动力学模型耦合响应模拟结果对比,蓝色与绿色实线分别表示波动力学模型及振动力学模型的耦合响应。图6a中波动模型相对振幅峰值位于203Hz处,振动模型位于285Hz处;图6b中波动模型的峰值位于618Hz处,振动模型的峰值位于620Hz处。由图6可见,在疏松、低速介质条件下两种模型耦合响应差别较大,波动模型较之振动模型耦合响应更趋低频,但在固结、高速介质环境中,两者耦合响应总体相近。
2.4两种模型模拟结果与实际数据对比
实际地震记录源自内蒙古某工区,表层调查资料显示该区表层土壤疏松,含水量较低,纵波速度在350~400m/s,泊松比在0.43~0.45。所用检波器尾锥长度0.1m,圆柱体半径0.005m,质量为0.4kg,机芯自然频率为60Hz。
由于检波器机芯在自然频率处存在谐振现象[21],需考虑其谐振响应Cresonate,具体表示为:
(13)
式中:Ccoupling表示耦合因素的响应,Coutput表示检波器整体响应输出。
图7为实测地震记录与波动及振动模型模拟

图6 不同介质条件下波动力学模型与振动力学模型耦合响应对比a 疏松介质条件; b 固结介质条件

图7 实测地震记录与波动及振动模型对比
记录对比,蓝色及绿色实线分别表示波动及振动力学模型模拟结果,红色实线表示实测记录的频率域振幅谱。由图7可见,实测地震记录的相对振幅曲线在59Hz处存在相对极值,两种模型也在临近61Hz处出现峰值。波动模型的另一峰值出现在203Hz处,与实测记录216Hz处的另一振幅极值接近。振动模型相对振幅峰值位于282Hz,在295~400Hz范围内的振幅趋势与实测记录幅值接近。
两种模型模拟结果与实测记录的振幅曲线在60Hz处重合,分析认为是检波器机芯谐振因素的影响所致。此外,在200~400Hz处,两种模型模拟结果与实测记录振幅曲线有一定程度的重合,波动模型在相对低频区域与实测记录接近,振动模型在相对高频区域与实测记录近似。由此可见,强调接触面紧密相连的波动力学理论同样适用于疏松、低速介质条件,而振动力学理论在相同条件下同样具有一定程度的局限性。
2.5两种模型叠加融合
鉴于波动与振动力学模型在200~400Hz内都具有一定拟合优势,且耦合响应的区间有所区别,本文在同等条件下将两种模型的数值模拟结果进行融合处理并转换为相对振幅值输出。融合算法为:

(14)
式中:Cresonate为检波器机芯谐振响应,Celastics为波动模型耦合响应,Cvibration为振动模型耦合响应,Coutput为检波器整体响应输出,A1与A2分别为波动及振动模型耦合响应的权重系数。
为了探讨数据融合的可行性,设置权重系数比例A1/A2=1。这种等权重系数的应用条件还需要进一步讨论研究,实际应用中可结合地表的介质条件进行适当调整。例如,针对灰岩等相对固结介质,波动力学模型更为适用,因此需要提高A1的权重比例。图8为波动模型和振动模型融合结果与实际记录对比,蓝色实线代表波动与振动模型的融合模拟值,红色实线代表实测记录相对振幅值。由图8可见,融合模拟结果的峰值在临近60Hz的区域与实测记录中的相对极值重合。在200~400Hz内,融合模拟结果与实测记录峰值接近且曲线形态大致相同,考虑到地下介质对地震信号具有滤波作用,可认为该对比结果较为合理。由此可见,融合波动模型与振动模型的方法能有效模拟实际条件下的耦合响应。
应该注意的是,两种模型融合结果在60~200Hz与实测记录存在较大出入,原因可以归结为两点:①两种耦合模型均以频率域幅值为1的阶跃函数作为输入信号,因此输出响应的频率成分也较为单一,而实际激发的地震波频谱比较复杂;②实测地震记录由于包含了部分来自地下深部反射层的反射信息,因此其频率成分也相对丰富。

图8 波动模型及振动模型融合结果与实际记录对比
3总结与讨论
本文构建了基于弹性波动力学的检波器-介质耦合系统模型,通过数值模拟分析得出以下结论:
1) 波动力学模型能有效模拟系统的耦合响应。
2) 土壤介质的速度、泊松比以及检波器尾锥半径是影响系统耦合响应的重要因素。
3) 波动力学模型与传统的振动力学模型在固结、高速介质中的耦合响应相近,在疏松、低速介质中存在一定差异。
4) 两种模型在模拟实际耦合情形时,具有不同的优势区间与局限性,通过引入融合算法,能发挥两者优势,较为有效地模拟实际条件。
鉴于融合波动模型与振动模型具有解决实际耦合问题的潜力,下一步有必要对融合算法进行深入研究。
参考文献
[1]邸志欣,丁伟,王增明,等.复杂山前带地震勘探采集技术的实践与认识[J].石油物探,2012,51(6):548-561
DI Z X,DING W,WANG Z M,et al.Practice and understanding of seismic acquisition technology in complicated foothill area[J].Geophysical Prospecting for Petroleum,2012,51(6):548-561
[2]魏继东.地震检波器性能指标与地球物理效果分析[J].石油物探,2013,52(3):265-274
WEI J D.An analysis on the performance indexes and geophysical effect of geophones[J].Geophysical Prospecting for Petroleum,2013,52(3):265-274
[3]吕公河.地震勘探中振动问题分析[J].石油物探,2002,41(2):154-157
LV G H.An analysis of viberation problem in seismic exploration[J].Geophysical Prospecting for Petroleum,2002,41(2):154-157
[4]邸志欣,丁伟,吕公河,等.五号桩地区滩浅海高精度三维地震采集技术[J].石油物探,2012,51(4):388-397
DI Z X,DING W,LV G H,et al.3D high-precision seismic acquisition techniques in Wuhaozhuang beach and shallow sea area[J].Geophysical Prospecting for Petroleum,2012,51(4):388-397
[5]吕公河,张光德,尚应军,等.胜利油田高精度三维地震采集技术实践与认识[J].石油物探,2010,49(6):562-572
LV G H,ZHANG G D,SHANG Y J,et al.Research and application of high-precision 3D seismic data acquisition technology in Shengli Oilfield[J].Geophysical Prospecting for Petroleum,2010,49(6):562-572
[6]魏继东,丁伟.检波器野外组合因素对地震资料品质的影响分析[J].石油物探,2010,49(3):312-318
WEI J D,DING W.Impact analysis of geophone array factors on seismic data quality[J].Geophysical Prospecting for Petroleum,2010,49(3):312-318
[7]董世学,张春雨.地震检波器的性能与精确地震勘探[J].石油物探,2000,39(2):124-130
DONG S X,ZHANG C Y.Seismic geophone property and precise seismic exploration[J].Geophysical Prospecting for Petroleum,2000,39(2):124-130
[8]吕公河.高精度地震勘探采集技术探讨[J].石油地球物理勘探,2005,40(3):261-266
LV G H.Discussion of high-precision seismic prospecting acquisition technology[J].Oil Geophysical Prospecting,2005,40(3):261-266
[9]KROHN C E.Geophone ground coupling[J].Geophysics,1984,49(6):722-731
[10]徐锦玺,吕公河.检波器尾锥结构对地震采集信号的影响[J].石油地球物理勘探,1999,34(2):204-209
XU J X,LV G H.The influence of geophone tailcone structure upon acquired seismic signals[J].Oil Geophysical Prospecting,1999,34(2):204-209
[11]徐淑合,刘怀山,童思友,等.准噶尔盆地沙漠区地震检波器耦合研究[J].青岛海洋大学学报,2003,33(5):783-790
XU S H,LIU H S,TONG S Y,et al.Study on seismic geophone coupling in desert area of Zhunger Basin[J].Journal of Ocean University of Qingdao,2003,33(5):783-790
[12]石战结,田钢,董世学,等.沙漠地区地震检波器耦合的高频信号匹配滤波技术[J].石油物探,2005,44(3):261-263
SHI Z J,TIAN G,DONG S X,et al.Match filtering of geophone coupling for high-frequencies of seismic data in desert area[J].Geophysical Prospecting for
Petroleum,2005,44(3):261-263
[13]刘志田,吴学兵,王文争,等.地震勘探采集中尾锥因素对检波器耦合系统的影响[J].中国石油大学学报:自然科学版,2006,30(3):26-29
LIU Z T,WU X B,WANG W Z,et al.Effects of tail-cone on geophone coupling system during seismic exploration[J].Journal of China University of Petroleum(Edition of Natural Science),2006,30(3):26-29
[14]石战结,田钢,谷社峰,等.检波器与灰岩地表耦合效应的理论和试验研究[J].石油地球物理勘探,2011,46(4):529-534
SHI Z J,TIAN G,GU S F,et al.Theoretical study and tests on geophone-limestone coupling effect[J].Oil Geophysical Prospecting,2011,46(4):529-534
[15]石战结,田钢,沈洪垒,等.灰岩裸露区检波器三自由度耦合系统理论的研究[J].地球物理学报,2010,53(5):1234-1246
SHI Z J,TIAN G,SHEN H L,et al.Theoretical studies of the geophone coupling influence in the limestone outcrops area[J].Chinese Journal of Geophysics (in Chinese),2010,53(5):1234-1246
[16]RADEMAKERS F,DRIJKONINGEN G G,FOKKEMA J T.Geophone ground coupling:new elastic approach[J].Expanded Abstracts of 66thAnnual Internat SEG Mtg,1996:1083-1086
[17]DRIJKONINGEN G G,RADEMAKERS F,SLOB E C,et al.A new elastic model for ground coupling of geophones with spikes[J].Geophysics,2006,71(2):Q9-Q17
[18]AKI K,RICHARDS P G.Quantitative seismology:theory and methods[M].San Francisco:W H Freeman and Company,1980:1-183
[19]DE HOOP A T.Handbook of radiation and scattering of waves:acoustic waves in fluids,elastic waves in solids,electromagnetic waves:with corrections[M].New York:Academic Press,1995:289-597
[20]FOKKEMA J T,VAN DEN BERG P M.Seismic applications of acoustic reciprocity[M].New York:Elsevier Science Pub Co Inc,1993:95-103
[21]吕公河.地震勘探检波器原理和特性及有关问题分析[J].石油物探,2009,48(6):531-543
LV G H.Analysis on principles and performance of seismic geophone and relevant issues[J].Geophysical Prospecting for Petroleum,2009,48(6):531-543
(编辑:戴春秋)
Geophone-media coupling system based on elastic wave dynamics
CHEN Gaoxiang,TIAN Gang
(SchoolofEarthSciences,ZhejiangUniversity,Hangzhou310027,China)
Abstract:The coupling effect between geophones and media plays a key role in data acquisition during seismic exploration.This paper introduces a study on coupling problem based on elastic wave dynamics.By building coupling model and comparing the outputs with the simulating results from vibration mechanics model,we illustrate how different media or geophone conditions affect the coupling responses and what differences is between two models.A method combining the data from elastic model with the data from vibration mechanics model is proposed next,and the feasibility of implement is also discussed through comparing with real seismic data.
Keywords:geophone,coupling system,elastic wave dynamics,vibration mechanics theory,Green function
收稿日期:2015-11-18;改回日期:2016-03-01。
作者简介:陈高翔(1991—),男,硕士在读,主要从事检波器耦合研究工作。
基金项目:国家高技术研究发展计划(863计划)项目(2013AA064202)资助。
中图分类号:P631
文献标识码:A
文章编号:1000-1441(2016)03-0333-08
DOI:10.3969/j.issn.1000-1441.2016.03.003
This research is financially supported by the National High-tech R&D Program (863 Program) (Grant No.2013AA064202).
——一致性函数,相关运算以及传递函数分析

