储层地震岩石物理建模研究现状与进展

印兴耀,刘欣欣

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071;3.国土资源部海洋油气资源与环境地质重点实验室,山东青岛266071;4.国土资源部青岛海洋地质研究所,山东青岛266071)

储层地震岩石物理建模研究现状与进展

印兴耀1,2,刘欣欣3,4

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071;3.国土资源部海洋油气资源与环境地质重点实验室,山东青岛266071;4.国土资源部青岛海洋地质研究所,山东青岛266071)

摘要:岩石物理建模是地震岩石物理研究的重要内容之一。基于双相介质和等效介质理论,将地震岩石物理建模的理论框架分为岩石基质、岩石骨架、孔隙填充物和饱和岩石四部分,在该理论框架下对现有地震岩石物理建模基本理论及各理论模型的假设条件和适用范围进行了阐述;针对碎屑岩、碳酸盐岩、致密砂岩、页岩等不同类型储层岩石的矿物组分、微观孔隙结构及孔隙填充物性质等,在探讨岩石物理建模现状及难点的基础上,对目前较为适用的建模方法进行了论述。研究表明,在充分考虑储层微观特征、有效利用多种资料的基础上建立的地震岩石物理模型,可有效描述储层微观物性特征和宏观弹性性质之间的定量关系,为储层定量解释、流体识别等提供可靠的依据。

关键词：岩石物理模型;等效介质理论;孔隙结构;非均质储层;弹性参数;Xu-White模型

随着勘探开发目标日益趋于复杂和隐蔽,碳酸盐岩等特殊岩性油气藏、致密砂岩和页岩等非常规油气藏逐渐成为油气勘探开发专家研究的热点。这些油气藏储量丰富,分布区域广,但其宏观空间构造以及微观结构的非均匀性导致弹性参数及地震响应不均匀变化[1],增加了储层地震解释、反演以及储层描述的难度。随着勘探难度的增加,对地震数据的分析已从地质体构造解释发展到储层岩性、流体的识别,而地震特性是地层构造、压力、温度、储层微观结构等诸多因素的综合反映,复杂的孔隙流体类型、骨架类型、孔隙度等微观因素均可能造成流体识别假象。地震岩石物理是联系储层特征与地震特性的桥梁[2],主要研究与地震特性有关的岩石物理性质以及这些物理性质与地震响应之间的关系,对地震正演和反演结果的定量解释有着重要的意义。

岩石的物理性质主要由岩石组分(矿物组分、孔隙度、孔隙填充物等)、岩石内部结构(矿物颗粒形状、排列、胶结程度、孔隙大小、形状、连通性、排列方式及其它不连续界面的分布、孔隙流体分布情况等)及其所处的热力学环境(温度、压力等)三方面的特征决定。岩石通常可以描述为固体骨架和孔隙流体组成的双相介质,当地震波波长远大于岩石的非均匀尺度(颗粒尺度)时,可将岩石等效为统计意义上的均匀物体,使用等效介质的概念来描述和表征岩石特性。地震岩石物理建模是指通过合理的假设把实际岩石等效为理想介质,使用物理学原理建立储层岩石物性参数与弹性参数的量化关系[3],是地震岩石物理研究的重要内容之一。

最早的岩石物理模型要追溯到80多年前VOIGT与REUSS提出的等应变和等应力模型[4-5]。目前广泛应用的是Gassmann方程,该方程通常被用来研究饱和流体对岩石弹性特征的影响,是近代沉积岩的弹性理论与岩石物性研究的基础。岩石物理模型主要包括三类:①对矿物性质进行体积平均的有效介质模型(Voigt-Reuss-Hill模型、Hashin-Shtrikman模型、Wood方程、Wyllie方程、Raymer方程等);②研究岩石内部孔隙结构和孔隙充填物对岩石性质影响的自适应和散射理论模型(DEM模型、Kuster-Toksöz模型、自适应模型、Gassmann方程等);③基于颗粒接触关系的接触理论模型(Hertz-Mindlin模型、Digby模型、Walton模型、Brandt模型等)。在考虑适用条件的基础上,XU等综合利用Wyllie方程、DEM模型、Kuster-Toksöz模型以及Gassmann方程建立了砂泥岩储层的岩石物理模型[6],为储层地震岩石物理建模确定了理论框架。针对不同类型储层的微观结构特征,Xu-White模型的改进形式以及一些新的模型被相继提出,并在许多地区的横波速度计算[7-8]、叠前地震反演[9]、岩石物理分析[10-11]、流体识别[12-13]、孔隙度反演和流体饱和度预测[14-15]等研究中取得了较好的应用效果。

实际岩石的组成、内部结构以及所处的热力学环境非常复杂,且不同岩性、不同区域差别很大。尤其是特殊岩性油气藏和非均质性较强的非常规油气藏,储层微观特征的复杂性和多样性对现有模型的适用性提出了很大挑战,经验公式或者经验参数很难得到推广应用,直接利用现有的岩石物理理论及模型指导地震定量解释存在很大风险,甚至可能出现错误的结果。因此,我们要根据实际储层的岩石物理性质探索更具适用性的岩石物理模型,同时根据模型的实际意义综合运用地质、测井、岩心、地震等资料提高建模结果的准确性。

我们对现有地震岩石物理建模基本理论及其假设条件和适用范围进行阐述,对不同类型储层岩石物理建模的现状及难点进行分析,并对目前较为实用的方法进行论述。

1地震岩石物理建模基本理论

根据Xu-White模型所使用的地震岩石物理建模理论框架,将岩石等效为岩石基质、岩石骨架、孔隙填充物及饱和岩石四个部分。其中矿物组分的混合物称为岩石基质,岩石基质中包含空孔隙的部分称为岩石骨架,孔隙中充满流体或固体等充填物后的岩石骨架称为饱和岩石。此处的孔隙指的是广义孔隙,即岩石中的空隙空间,包括狭义的孔隙、溶洞和裂缝[16]。

1.1岩石基质等效模型

1.1.1Voigt-Reuss-Hill模型

该模型用于计算各向同性线弹性固体矿物混合物的等效弹性模量,要求矿物混合物及各组成成分满足各向同性、线性、弹性假设。Voigt提出等应变平均[4],是N种矿物混合物的有效弹性模量的上限;Reuss提出等应力平均,是矿物混合物的有效弹性模量下限[5]。实际岩石测量得到的模量参数必定落在Voigt模型和Reuss模型的估计值之间。Hill提出将这两种模型的结果取算术平均值[17],即:

(1)

(2)

(3)

式中:fi是第i种组分的体积含量;Mi是第i种组分的弹性模量。公式(1)至公式(3)分别为Voigt上限、Reuss下限和Hill平均方程。给定岩石的矿物成分和孔隙空间时,Voigt-Reuss-Hill模型(简称VRH模型)可用于估算岩石的等效弹性模量,还可用于估算中等孔隙度的饱含水砂岩的等效体积模量,但不适用于计算饱含气砂岩的等效模量或饱和流体岩石的等效剪切模量。当矿物混合物有一个构成成分是液体或气体(零剪切模量)时,用Reuss下限计算的体积模量和剪切模量与Hashin-Shtrikman下限计算的结果一致。Kumazawa提出使用Voigt和Reuss界限的几何平均[18];Marion提出使用边界之间垂向相对位置作为加权系数(表示孔隙细节,且与孔隙充填物的性质无关),对上、下限进行加权平均,但在使用时需要根据已知资料对加权系数进行求取或标定[19]。

1.1.2Hashin-Shtrikman界限

Hashin和Shtrikman提出了不同组分混合弹性体模量的最窄界限[20],即Hashin-Shtrikman界限(简称HS界限):

(4)

(5)

式中:Ki和μi(i=1,2)分别是各构成成分的体积模量和剪切模量。Berryman将HS界限推广到多相介质的形式[21],可用于计算矿物基质或矿物与流体混合的弹性模量的上下限。该模型要求混合物及各组成成分满足各向同性、线性、弹性假设,上下限之间的差异大小依赖于各成分间弹性性质差异的大小,当几种固体混合时上下限很接近,当几种成分之间差别很大时(如矿物和孔隙流体)上下限之间的差异很大,预测能力变差。孙晟等推导了孔隙内含流体的HS界限公式,弥补了经典HS界限对整体弹性模量特别是孔隙度小于20%时剪切模量估算的不足[22]。

1.2岩石骨架等效模型

1.2.1Kuster-Toksöz模型

Kuster和Toksöz使用孔隙纵横比(椭球体短轴与长轴的比值)来描述孔隙形状,基于散射理论建立了岩石的弹性模量与孔隙度和孔隙形状之间的联系。假设岩石有两种或两种以上的孔隙结构,且各类孔隙的纵横比各不相同,则Kuster-Toksöz模型(简称KT模型)可表示为[23-24]:

(6)

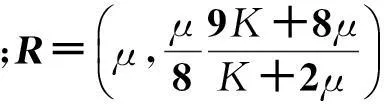
1.2.2微分等效介质(DEM)模型

Berryman模拟将孔隙按一定增量逐渐加入岩石基质的过程建立了DEM模型,提出了体积模量和剪切模量耦合的微分方程[25]:

(7)

K*(0)=Kgr

(8)

式中:K*表示岩石基质逐渐加入包含物后的弹性模量,K2表示逐渐加入的包含物的弹性模量。DEM模型计算的弹性模量始终处在HS上下边界范围内[26],不同类型孔隙的加入顺序会影响最终计算结果[27]。如果直接将DEM模型应用于流体饱和孔隙,则会由于没有考虑孔隙系统中的流体位移产生一个孤立孔隙模型或高频声波模型。

微分方程(7)和(8)缺乏解析式,ZIMMERMAN从球形孔隙的DEM方程推导出干岩石骨架弹性模量的隐式解析式[28]。KEYS等利用干岩石近似将DEM方程简化为体积模量和剪切模量解耦的线性表达式[29]。BERRYMAN基于DEM理论得到干燥和完全饱和裂隙型岩石弹性模量的近似解析式[30]。李宏兵等在假设干岩石体积模量和剪切模量的几何因子线性相关的前提下,基于DEM理论推导出干燥岩石体积和剪切模量及弹性模量比的显式解析式,并将其应用于横波速度预测,反演各孔隙类型的孔隙体积比[31-33]。杨凤英等将几何因子写为下面的统一形式[34-35]:

(9)

式中:y为包含物体积含量,P=(P,Q)是与孔隙纵横比有关的几何因子,P(0)=(P(0),Q(0))为仅与包含物几何形状有关的常数,P(1)=(P(1),Q(1))为包含物体积含量的一次项系数。由此得到可变干岩石骨架等效岩石物理模型(VDEM模型):

(10)

VDEM模型将DEM解耦为常微分方程组,扩展了DEM模型的适用性,已被成功应用于碎屑岩储层横波速度计算。

1.2.3自洽模型

自洽模型也称自相容近似模型(简称SCA模型)。其基本思想是假设待求解的多孔介质位于无限大基质中,不断调整基质的弹性参数,直到平面波入射时多孔介质不再引起散射为止。此时多孔介质的弹性模量可以等效为基质的有效弹性模量[36-37]。BERRYMAN基于弹性波散射理论提出计算含椭圆包含物岩石的等效体积和剪切模量[38-39]:

(11)

式中,fi为第i种包含物的体积含量。该模型的局限性在于假设孔隙互不连通且波长远大于包含物的尺寸,是KT模型的更一般形式,适用于孔隙度较大的岩石。如果孔隙纵横比较小,那么该模型的使用必须慎重。自洽模型已经被推广到不同形状包含物对岩石弹性模量的影响[40-41]、裂隙以及裂隙间相互作用对岩石弹性模量的影响[42-43]、多相介质并存情况下岩石的弹性模量[44]等计算中。

1.3流体等效模型

1.3.1Wood模型

对于孔隙或者裂隙中的流体混合物,WOOD推导了流体悬浮或流体混合物非均匀性小于波长时的声波速度[45]:

(12)

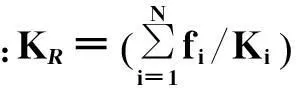
1.3.2Wyllie方程

WYLLIE等提出充满盐水的多孔介质的孔隙度与速度之间满足经验关系[46]:

(13)

式中:v,vm和vf分别为整体岩石、岩石基质和孔隙流体的速度;φ为孔隙度。(13)式表示波在岩石中传播的总时间等于其在岩石骨架中传播的时间与其在孔隙流体中传播的时间之和,也称为时间平均方程,可用于计算有效压力较高时流体饱和岩石的速度-孔隙度关系,但岩石必须是各向同性的、流体饱和的,只含有一种均匀的矿物组分,适用于中等孔隙度的岩石,不适用于未固结、未压实的岩石,而且计算出的含粘土砂岩的纵波速度值偏高。

Wyllie方程较适用于孔隙度范围适中(10%～25%)的纯砂岩,RAYMER等将其推广到更大的孔隙度范围[47]。ANGELERI等考虑泥质含量对速度的影响,将Wyllie方程推广到三相介质[48];KAMEL等将Wyllie方程与声地层因素方程Raiga-Clemenceau相乘,得到确定纯砂岩地层孔隙度的方程[49]。

1.4饱和岩石等效模型

1.4.1Gassmann方程

Gassmann推导出宏观各向同性的饱和岩石立方体体积模量表达式[50]:

(14)

式中:α=1-Kdry/Kgr;Ksat,Kfl分别为饱和岩石和孔隙流体的体积模量。Gassmann理论认为,饱和岩石的剪切模量与岩石骨架的剪切模量相等。方程(14)的基本假设条件:①岩石受到静态或者低频形变;②岩石(基质和骨架)是微观各向同性和宏观均匀的;③所有孔隙都充满了无摩擦流体(液体、气体或两者的混合物);④孔隙空间完全连通,流体压力平衡;⑤孔隙流体与岩石骨架之间不会发生任何物理或化学的相互作用。BIOT[51-52]、唐晓明[53]考虑高频条件下流体与固体的相互运动,将Gassmann方程推广到了高频;BROWN等[54]推导出了Gassmann方程的各向异性形式,MAVKO等在弱各向异性假设下,引入与Thomson各向异性参数δ成比例的一阶校正项,推导出了地震波沿VTI介质同相轴传播时各向异性流体替换方程近似式[55];CIZ等将Brown&Korringa各向异性流体替换方程推广到孔隙充填物剪切模量不为零的介质[56];GRECHKA等将Gassmann方程推广到不连通孔隙[57]。

1.4.2Gassmann方程各向异性形式

BROWN等假设骨架是非均匀的,推导出了各向异性岩石骨架有效弹性模量与该骨架充填流体时的有效模量之间的理论关系式,即Gassmann方程的各向异性形式[54]:

(15)

式中:Ssat,Sdry和Sgr分别为饱和岩石、干燥岩石骨架及岩石基质的柔度张量;βfl和βgr分别是流体和岩石基质的可压缩系数;φ为孔隙度。该方程可用于各向异性岩石的流体替换,适用于低地震频带范围内的流体(剪切模量为零)完全饱和岩石。

1.4.3固体替换方程

CIZ等考虑围压和孔隙压力下骨架及孔隙填充物的微小形变,将Gassmann方程的各向异性形式推广到孔隙中充填固体物质时[56]:

(16)

式中,Sif为孔隙空间填充物的柔度,如果孔隙填充物剪切模量为0,则Sif退化为流体的压缩系数,(16)式退化为Brown&Korringa方程;Sφ为干燥多孔骨架中孔隙空间部分的柔度张量,对于各向同性岩石骨架,Sφ=Sgr。方程(16)可用于计算孔隙充填物的剪切模量不为零(如稠油)时岩石的有效弹性模量。当岩石的孔隙度非常高,比如超过50%时,干燥岩石骨架的柔度为0,那么(16)式变为:

(17)

也就是Reuss模型的更一般形式。

1.4.4斑块饱和模型

斑块饱和是指受岩石孔隙结构和流体饱和度的影响,部分饱和或多相饱和孔隙介质所呈现的孔隙流体在空间上的一种分布形式[58]。当弹性波通过含流体岩石时,孔隙内流体压力增加以均衡波动造成的压缩作用，对于单一流体完全饱和的岩石,此时弹性模量可用Gassmann方程进行描述,而对于部分饱和或多相流体饱和岩石,由于各流体组分的弹性性质有所差异,所产生的孔隙压力不尽相同。规模小于临界弛豫规模的每一斑块将达到流体相的平衡;而规模大于临界弛豫规模的相邻区块彼此将不会平衡,具有近似于Ruess平均(流体等应力混合)的状态。每一区块岩石的体积模量都不一样,但是剪切模量相同,即斑块饱和状态。这种岩石的有效体积模量可以表示为[59]:

(18)

式中:〈·〉表示对各成分按体积含量求加权平均。每一区块都具有不同的体积模量,可分别用Gassmann公式计算得到,剪切模量将保持不变。该理论可用于计算斑块饱和岩石的弹性模量,而且有效体积模量与其组成成分的体积含量有关,与该成分的几何形态等因素无关。

1.5Xu-White模型

HAN等通过实验证实,含水砂岩的纵、横波速度受孔隙度和粘土含量的影响很大,且高孔隙度和高泥质含量的岩石趋向于具有较高的纵横波速度比[60]。据此,XU和WHITE假设砂泥岩的主要矿物组分为石英和粘土,将岩石孔隙分为泥质孔隙和砂岩孔隙,按石英、粘土矿物组分的体积含量对总孔隙度进行加权得到两种孔隙的孔隙度,引入纵横比刻画孔隙形状,综合利用Wyllie方程、DEM模型、KT模型以及Gassmann方程,定量估算泥质砂岩的等效模量及纵横波速度[6](图1)。

图1　Xu-White模型地震岩石物理建模流程

Xu-White模型在储层横波速度计算和岩石物理分析中得到了广泛应用,但在某些实际工区的应用效果不尽人意,主要原因可能有以下两点:

1) 模型本身有一定的假设条件,得到的是实际储层的等效弹性性质。

2) 不同地区及同一地区不同深度的储层物性性质具有多样性,导致输入参数变化大,且难以准确获取。如Xu-White模型输入的砂泥岩孔隙纵横比是固定的经验值,而实际地层中孔隙纵横比与孔隙度和泥质含量等参数有关[61]。与矿物组分有关的石英和粘土模量参数取用经验值,而这些参数是前人根据不同的资料统计分析得到的,在不同的地区或采用不同的分析方法均可能有所不同[62-63]。如KATAHARA认为粘土的体积和剪切模量分别为50,20GPa[64];BERGE等认为粘土的体积模量为10～12GPa[65];VANORIO等认为粘土体积和剪切模量分别为6～12,4～6GPa[66]。

2非均质储层地震岩石物理建模

非均质储层的矿物组分和微观孔隙结构特征复杂,岩石物理模型建立起岩石微观物理性质和宏观弹性特征之间重要的联系。针对非均质储层,包括低孔隙度致密砂岩储层、孔缝洞共存的碳酸盐岩储层、有机质发育的页岩储层以及稠油储层等,根据岩石物理建模的理论框架,构建相应的地震岩石物理模型,建立了非均质储层微观物性参数与宏观弹性参数之间的定量关系。

2.1碎屑岩储层地震岩石物理模型

针对碎屑岩储层,PRIDE提出固结系数模型,利用纵波速度和孔隙度等计算横波速度[67]。LEE对Pride固结系数模型进行改进,通过使计算的纵波速度与实测值误差最小来反演固结系数,并用于横波速度计算[68],但是这类模型没有考虑岩石微观孔隙结构特征对宏观弹性性质的影响。近年来,Xu-White模型的实际应用日趋成熟,并出现了多种简化或者改进模型,但输入参数的确定是难点也是影响计算精度的重要因素。为此,郭栋等提出使用测井声波速度和密度约束反演的方法[69];邵才瑞等提出了利用叠前地震波形反演等对矿物组分模量、孔隙度等输入参数进行修正的方法[70],得到了较为可靠的横波速度,在地震奇异性属性提取和弹性阻抗反演中得到了成功应用[71-72]。熊晓军等利用Gassmann方程及Russell流体因子分别求取流体项,通过寻找两个流体项差值的最小值计算岩石基质的等效弹性参数以及岩石骨架的泊松比,提高了计算精度[73]。

2.1.1测井资料重构反演弹性模量

Xu-White模型物理意义明确,但其岩石基质模量、密度等输入参数通常不易直接获取,而且不同地区参数各异,相同地区的输入参数随深度变化也会发生改变,单一应用经验参数必然会引起较大的计算误差。为此,将实测声波测井资料作为约束条件,利用Xu-White模型及经验公式构建输入和输出参数之间的关系式,建立反演目标函数:

(19)

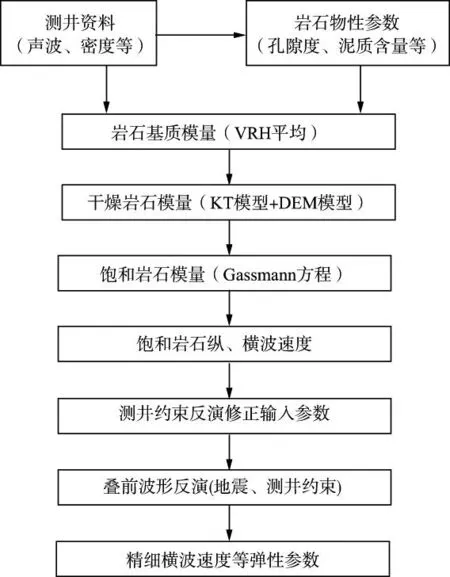
图2　测井曲线约束反演横波速度的流程

常用的反演算法包括模拟退火算法[74]、信息合取算法[75]等,反演约束条件多采用实测纵波速度曲线,反演修正的输入参数多为孔隙度。近年来出现了针对泥质含量和孔隙纵横比的修正方法[76],在实际应用中取得了不错的效果(图3)。由于Xu-White模型的输入参数较多,应根据实际情况针对影响较大的参数进行分析和确定,并充分利用已有的地质、测井、钻井和地震资料,最大限度地提高输入参数的可靠程度,提高计算结果的精度。印兴耀等以岩石孔隙参数为基础,建立测井数据与岩石弹性参数之间的岩石物理关系,在不使用速度测井信息作为约束的情况下能得到可信度较高的速度预测结果[77],为无实测纵波速度地区的横波速度预测提供了较好的思路。叶端南等基于微分等效介质理论构建了砂泥岩储层岩石物理模型,用于绘制弹性参数交会模板,可以合理界定出储层的砂、泥岩范围,为储层岩性的精细识别提供了新的途径[78]。

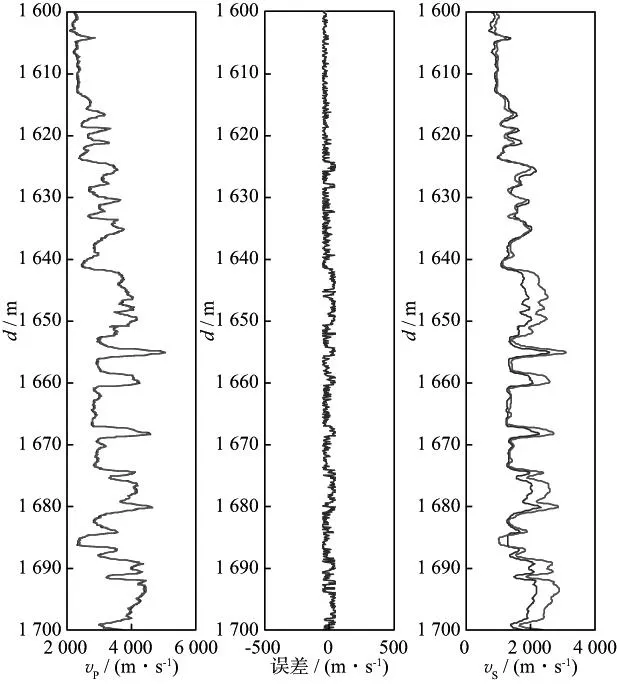
图3　反演修正孔隙度后计算的纵、横波速度

2.1.2叠前地震反演修正横波速度

地震数据能全面地反映地下介质的弹性性质,且与岩石性质和流体直接相关,因而从地震数据中获取弹性参数对于岩性油气藏勘探是非常必要的。将由测井曲线计算出的纵、横波速度和密度作为先验信息,利用正演方法计算叠前合成地震道集数据,将其与实际观测的CMP道集进行比较,根据二者的匹配程度得到能最佳描述本地区地质情况的模型,最终得到更有利于地层岩性精确预测的横波速度。对地下进行精确模拟需要计算成百上千层,利用需要求取目标函数导数信息的局部线性化反演方法非常困难,而且寻优效果受初始地层模型影响极大。

张繁昌等[79]利用遗传算法进行叠前地震波形反演,修正横波速度,并采用并行计算方法大大加快了计算速度。图4为叠前波形反演结果,原始叠前道集和合成记录两者主要反射同相轴对应较好,在一定程度上提高了横波速度的准确性。该方法在参数反演时加入了地震信息,实现了测井信息和地震信息的结合,使得反演得到的井数据的合成道集与实际道集之间在同相轴的位置、极性和幅度的变化方面更加一致,从而使得到的井数据更加可信。

2.2碳酸盐岩储层地震岩石物理模型

碳酸盐岩矿物组成复杂,包括方解石和白云石,经常混合少量的石英、粘土、无水石膏(硬石膏)或其它非碳酸盐自生矿物和陆源碎屑矿物。碳酸盐岩储层的孔隙系统比碎屑岩储层复杂得多,可能发育铸模孔隙、溶洞、粒间孔隙和粒内孔隙等多种类型的孔隙。许多学者针对已有模型在碳酸盐岩中的适用性研究指出,对于孔隙度较高和较低的地层,Gassmann方程分别过高和过低地估计了纵横波速度,但计算的纵横波速度比和实验室测量值接近[80],斑块饱和模型能预测更大的速度变化[81]。有些地区的碳酸盐岩储层可能表现出各向异性特征,Xu-White模型已被拓展应用到碳酸盐岩,成功应用于裂缝方位各向异性的预测[82]。基于岩石物理模型的量版技术在含气储层的定量预测中也得到了成功应用[83-84]。

图4　叠前波形反演结果a 计算的横波速度(虚线为岩石物理计算结果，实线为叠前波形反演修正后的结果); b 原始叠前道集; c 叠前波形反演后的叠前道集

碳酸盐岩储层岩石物理建模的主要难点在于岩石微观孔隙结构的定量表征。孔隙度和孔隙微观结构对岩石弹性性质有很大的影响[85-86],尤其是低纵横比孔隙,当孔隙度一定时,孔隙类型不同能够引起纵波速度高达40%的变化量[87]。国内外学者针对碳酸盐岩孔隙提出了基于岩石组构和岩石物理的分类[88]以及孔洞缝分类[89]等多种方案,根据实际的微观孔隙特征,提出了双孔隙模型[90-91]、孔缝洞三孔隙模型[92-93]、各向异性模型[94-95]等不同的岩石物理模型,结合方位各向异性弹性阻抗反演等方法,实现了含裂缝碳酸盐岩储层弹性参数和岩石物理参数的预测[96]。

岩石物理模型中对微观孔隙结构(各类孔隙的孔隙度和孔隙形状)进行合理的描述非常关键。目前常用的方法是根据已知测井资料等数据对孔隙结构参数进行反演估算,再利用地震岩石物理建模方法计算储层的弹性参数。常用的反演方法有测井曲线加权联合反演、模拟退火算法反演[97]以及遗传算法反演[98]等。图5至图7是对某碳酸盐岩工区进行孔隙微观结构反演及横波速度计算的结果。该区碳酸盐岩矿物主要是方解石和白云石,含有少量的泥质，储层内的孔隙流体主要是水和天然气。估算的横波速度与实测值的相关系数为0.94,平均相对误差为1.9%,平均绝对误差为59.9m/s,方差为77.1m/s,证明了方法的有效性。结合测井解释信息,可以进一步进行岩性或者流体岩石物理分析,为地震反演或者解释提供帮助和指导。

图5　反演求取各类孔隙的孔隙纵横比

碳酸盐岩储层的非均质性很强,需要明确各种理论模型的适用性,建立适用于复杂碳酸盐岩储层的岩石物理模型。对碳酸盐岩孔隙微结构进行合理的描述是计算弹性模量和横波速度的关键。在缺少岩心数据或者实验数据的情况下,充分利用工区已有的测井、地震资料,根据孔隙形状和连通性对碳酸盐岩孔隙进行划分,得到的孔隙微结构是实际岩石孔隙系统的等效近似,可以在一定程度上反映岩石中不同形状孔隙的构成情况。实际地层中的碳酸盐岩由于裂隙的定向排列可能表现出各向异性特征,相关的各向异性理论、方法及应用有待开展进一步研究。

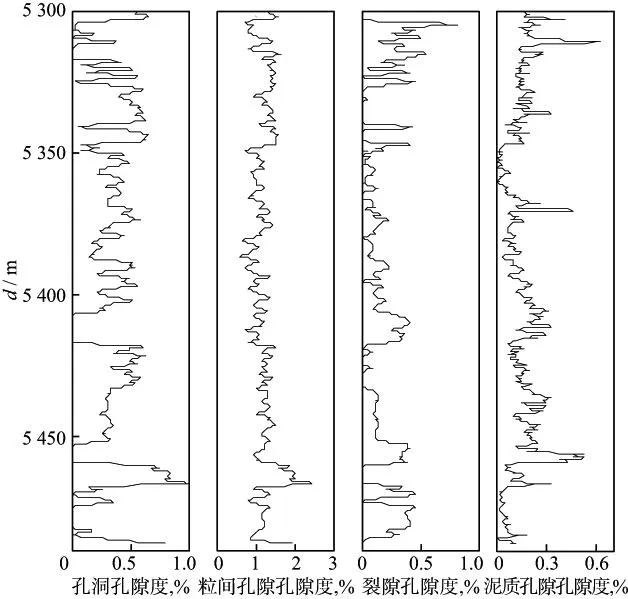
图6　反演求取各类孔隙的孔隙度

2.3致密砂岩储层地震岩石物理模型

致密砂岩储层通常具有低孔低渗以及孔隙结构复杂等特性,速度-孔隙度关系比较复杂。当岩石孔隙度小于10%时,孔隙结构是岩石弹性模量的主要影响因素,孔隙度的影响次之[99]。少量裂隙的存在会明显减弱岩石的弹性模量并降低地震波传播速度,同时,裂隙的存在导致流体的作用不明显,利用地震和测井资料进行流体预测的难度非常大[100]。致密储层的低渗透率特征意味着孔隙流体不能无摩擦地自由流动,不满足Gassmann理论的假设条件,而且Gassmann理论中没有考虑到孔隙类型,因此在致密砂岩储层中的适用性受到很大的挑战。针对致密砂岩储层进行岩石物理建模的难点主要在于对岩石微观孔隙结构参数,尤其是低纵横比孔隙结构的表征。

SMITH等使用KT模型计算低纵横比孔隙对岩石弹性性质的影响[99]。RUIZ等提出的软孔隙模型(Soft-Porosity Model)考虑了裂隙的影响,可用于致密储层的流体替换,是目前常用的致密砂岩地震岩石物理模型[100-101]。印兴耀等考虑孔隙和裂隙并存的情况,使用Biot相洽理论计算致密砂岩储层的弹性参数,并使用岩石骨架泊松比构建流体因子,能较好地区分出含气储层[102]。图8是使用实际声波测井资料作为约束条件反演求取裂隙孔隙度,并在Biot相洽理论框架下计算得到的致密砂岩弹性参数交会图,能较好地区分出高产气层与非气层。基于Biot相洽理论的岩石物理模型无需对除裂隙以外的孔隙进行描述,计算中得到的岩石骨架泊松比参数可用于Russell流体因子的构建,提高了储层流体参数分析的可靠性。李龙考虑了低孔低渗岩石的频率特征以及孔隙与裂缝之间的流体流动,结合Chapman孔隙-裂缝衰减模型和SCA模型构建了高频地震岩石物理模型[103],将纵波速度曲线作为约束条件,利用模拟退火算法反演岩石的软孔隙与硬孔隙成分,根据图9所示的横波速度计算流程,得到的横波速度如图10所示。由图10可见估算的横波速度与实测速度吻合程度较高,说明所建立的高频岩石物理模型对于致密储层岩石具有较好的适用性。

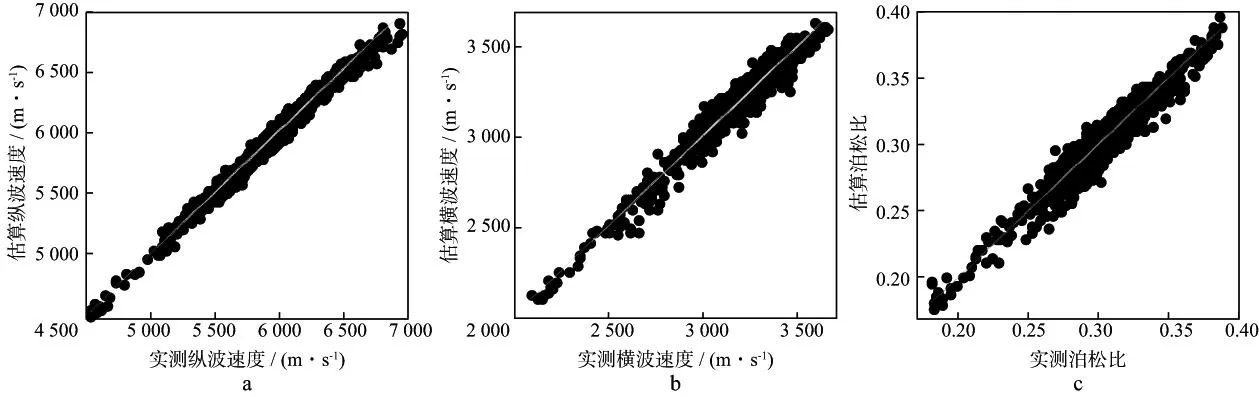
图7　纵(a)、横(b)波速度和泊松比(c)计算结果与实测值交会分析

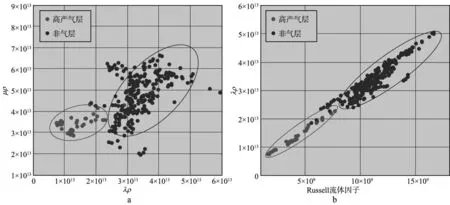
图8　基于Biot相洽理论岩石物理模型计算的某井流体敏感参数交会分析a λρ和μρ交会分析; b Russell流体因子和λρ交会分析

致密砂岩储层中微裂隙的存在为油气的运移提供了通道,同时也为地震流体识别带来挑战,如何更好地模拟微裂隙及其中的流体对致密砂岩储层弹性性质的影响仍是目前研究的重点。

2.4页岩储层地震岩石物理模型

页岩储层由细粒物质组成,岩石成分复杂,包括粘土、石英、方解石、白云石或硫铁矿等无机矿物和干酪根等有机质,并且存在大量吸附气;储层孔隙空间多样,孔隙度和渗透率较低,裂缝或裂隙是影响产能的重要因素[104]。页岩气储层中的有机质是产气能力的指示,有机质的存在使得页岩纵横波速度、密度、纵横波速度比降低[105],各向异性增强[106-107]。有机碳总含量和矿物成分在很大程度上影响岩石的强度和脆性,导致杨氏模量和泊松比随岩石物理参数(包括有机碳含量)的变化很大。

页岩储层的岩石物理建模主要是针对有机质以及岩石各向异性的研究。HORNBY等联合使用SCA和DEM模型模拟各向异性页岩的弹性性质[108]。BAYUK等将干酪根作为模型,将孔隙或裂隙等加入到干酪根-粘土基质中,利用测井数据反演重构岩石微结构参数,然后计算低频条件下岩石的速度[109]。COOPE等提出了泥、有机质和流体共存的岩石物理模型,根据核磁共振和随钻测井资料来实时评估页岩气储层中的有机碳[110]。SUN等提出各向异性双孔隙模型(ADP模型),使用SCA,DEM和各向异性Gassmann方程计算页岩储层的弹性参数,成功计算了实际储层的速度[111]。VERNIK等提出页岩的各向异性岩石物理模型,并将其应用到脆性指数计算和AI-SI反演[105,112]。CARCIONE等使用Backus和Krief/Gassmann模型对油饱和岩石进行模拟,发现岩石速度与总有机碳(TOC)含量有很大的相关性[113]。ZHU等认为有机质对于页岩岩石地震特性和电学性质有较大影响,采用Gassmann方程和各向异性Brown & Korringa公式分别进行流体替换和固体替换,从而计算出页岩储层弹性参数[114]。董宁等引入Berryman三维孔隙形态及Brown-Korringa固体替代技术得到适用于页岩的岩石物理模型[115]。胡起等通过融合各向异性DEM理论和Brown-Korringa各向异性流体替换模型,建立了有机页岩各向异性岩石物理模型,提出了根据纵波速度反演岩石等效孔隙纵横比,进行页岩气储层横波速度预测的方法[116]。李龙认为[103],在渗透率极低的致密储层,速度衰减的特征频率小于声波测井的频率,在声波测井的频率范围内速度的衰减和频散不明显,可以使用高频的岩石物理模型。他将孔隙归纳为随机分布于岩石中的刚性孔隙和定向排列的泥岩裂缝,考虑有机质的存在以及岩石的各向异性特征,采用各向异性自洽模型计算页岩孔隙流体对弹性特征的影响,并利用实验室数据与实际工区测井数据验证了页岩储层地震岩石物理模型的适用性(图11,图12)。张广智等提出了适用于页岩储层的岩石物理等效模型建立流程,并以此为基础实现了最小水平地应力的有效预测[117]。

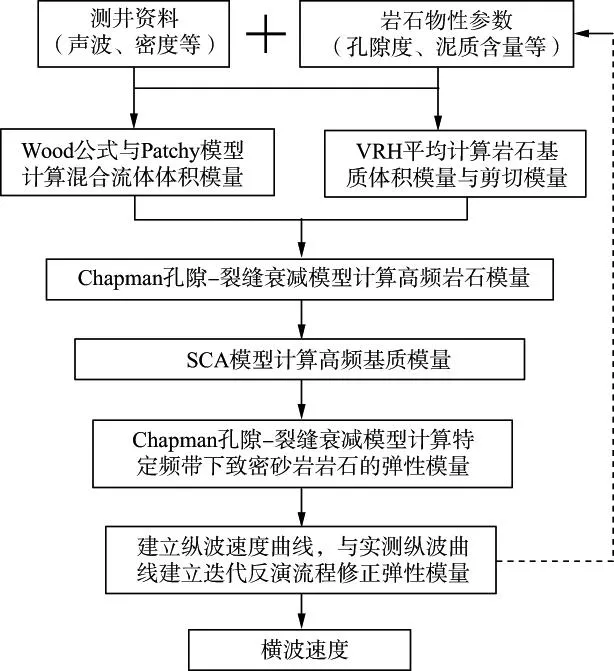
图9　基于高频岩石物理模型的横波速度计算流程

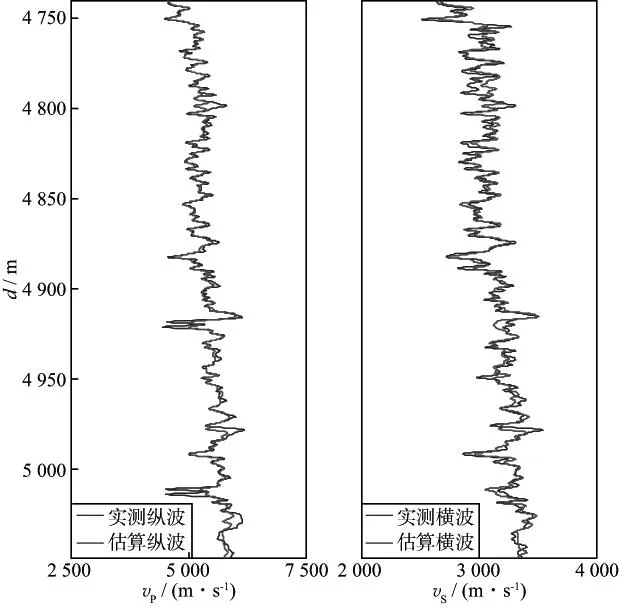
图10　高频岩石物理模型纵、横波速度计算结果

实验证明,页岩中可能存在大量的纳米级孔隙[118],而目前的岩石物理模型重点考虑了孔隙的形状,忽略了孔隙的大小。在上述页岩岩石物理模型中,有机质或者作为固体基质的一部分,或者作为孔隙填充物的一部分,或者同时作为上述两种组分。具体采用何种模型取决于实际页岩储层的物理性质,因此在进行岩石物理建模前需要根据地质、钻井、录井资料等对有机质的赋存状态、与矿物组分之间的接触关系、定向排列等特征进行分析和刻画,以提高岩石物理模型的可靠性。

图11　页岩储层横波速度计算流程

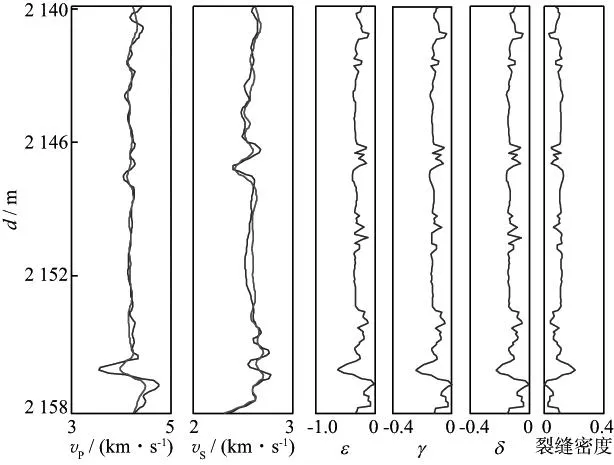
图12　某井资料横波计算结果

2.5特殊孔隙充填物岩石地震岩石物理模型

在岩石孔隙中,稠油、有机质等剪切模量不为零的充填物的存在使得岩石性质与油气水饱和岩石的性质大不相同,给地震资料的反演解释带来了挑战。石油的粘滞性不符合Gassmann理论的各向同性假设等限制条件,目前考虑孔隙充填物剪切性质的岩石物理模型研究仍处于起步阶段,BATZLE等与BEHURA等考虑岩石中流体的性质(包括流体的粘滞性)指出,Maxwell模型的频率相关性比实际实验室观测数据强[119-120]。HAN等研究了稠油饱和砂岩中速度的不同影响因素,指出在60℃以下稠油会发生频散,Gassmann方程不再适用[121-123]。

GURVICH等综合了Cole和Cole-Maxwell模型的弛豫谱,改进了计算粘滞性流体的横波速度频散关系(简称CCM模型),使用相干势近似(CPA)进行重油岩石的流体替换[124]。DAS等根据自洽和DEM模型计算粘滞性流体饱和岩石的模量,但该方法对未固结砂岩不适用[125-126]。MAKARYNSKA等提出基于有效介质理论通过岩石成分和微观结构来估计弹性模量的方法,在足够低频时,该方法可用于多个粘弹性组分混合的情况[127]。吴志华建立了CXW模型(CPA模型与Xu-White模型相结合的模型)和XWGG模型(Xu-White模型与广义Gassmann模型相结合的模型),并将其成功应用于含稠油的碎屑岩和碳酸盐岩储层横波速度计算(图13至图16)[128]。目前这类模型大多针对充填物的剪切特征进行描述和计算,没有考虑充填物与岩石矿物组分或者流体之间的相互作用,更为适用的岩石物理模型还有待进一步研究。

图13　基于CXW模型的弹性参数计算流程

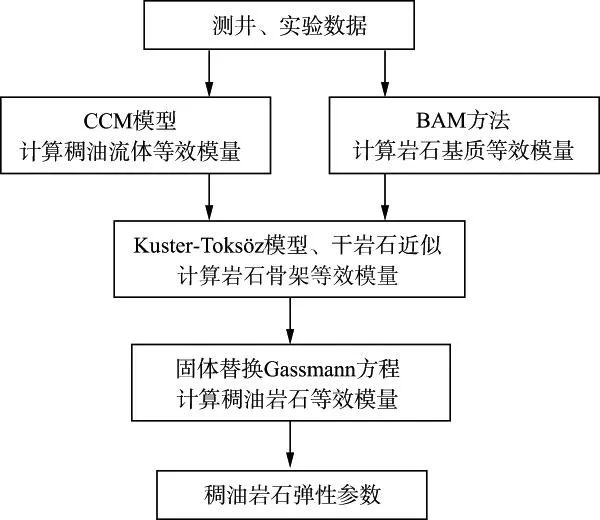
图14　基于XWGG模型的弹性参数计算流程

图15　CXW模型纵、横波速度估算结果

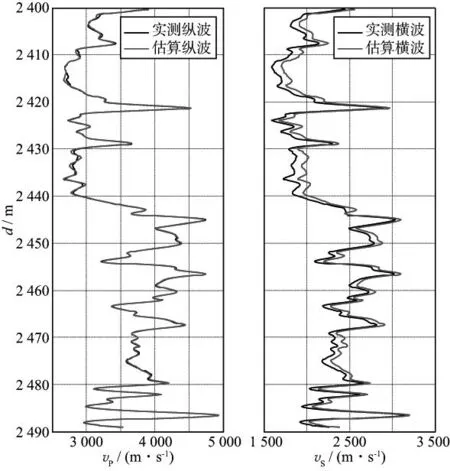
图16　XWGG模型纵、横速度估算结果

3认识和展望

考虑储层岩石的矿物组成、孔隙微观结构特征,基于双相介质假设和等效介质假设,采用地震岩石物理建模方法可有效地计算储层的弹性参数。但是任何一种岩石物理模型都建立在一定的假设条件之上,有特定的适用范围,若要更准确地建立岩石物理模型,就要综合利用地震、测井、地质等信息对输入参数进行标定,并使用多种资料作为约束条件减少反演多解性,提高储层弹性参数计算精度。目前岩石物理模型多是基于低频假设和长波长假设建立的,因此各类资料间的频率和尺度问题还有待进一步研究。

虽然地震勘探目标的复杂性和多样性对地震岩石物理建模提出了挑战,但实验室测量技术的不断进步使得储层微观特征的描述越来越精细,计算机模拟技术的进步也促使数字岩心等技术得到很好发展,这些都为储层地震岩石物理建模提供了很好的依据和有力的支持。未来针对不同储层的地震岩石物理模型将能更加准确地描述储层微观特征与宏观弹性特征的定量关系,为储层定量解释、流体识别等提供可靠的依据。

参考文献

[1]戴启德,纪友亮.油气储层地质学[M].北京:石油工业出版社,1996:1-32

DAI Q D,JI Y L.Petroleum reservoir Geology[M].Beijing:Petroleum Industry Press,1996:1-32

[2]MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook:tools for seismic analysis in porous media[M].Cambridge:Cambridge University Press,1998:106-220

[3]马淑芳,韩大匡,甘利灯,等.地震岩石物理模型综述[J].地球物理学进展,2010,25(2):460-471

MA S F,HAN D K,GAN L D,et al.A review of seismic rock physics models[J].Progress in Geophysics,2010,25(2):460-471

[4]VOIGT W.Lehrbuch der kirstallphysik[M].Leipzig:Teubner,1928:739

[5]REUSS A.Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals[J].Zeitschrift fur Angewandte Mathematik,1929(9):49-58

[6]XU S,WHITE R E.A new velocity model for clay-sand mixtures[J].Geophysical prospecting,1995,43(1):9l-118

[7]ZHANG J J,LI H B,YAO F C.Rock critical porosity inversion and S-wave velocity prediction[J].Applied Geophysics,2012,9(1):57-64

[8]谢月芳,张纪.岩石物理模型在横波速度估算中的应用[J].石油物探,2012,51(1):65-70

XIE Y F,ZHANG J.Application of rock physical model in S-wave velocity estimation[J].Geophysical Prospecting for Petroleum,2012,51(1):65-70

[9]印兴耀,曹丹平,王保丽,等.基于叠前地震反演的流体识别方法研究进展[J].石油地球物理勘探,2014,49(1):22-34,46

YIN X Y,CAO D P,WANG B L,et al.Research progress of fluid discrimination with pre-stack seismic inversion[J].Oil Geophysical Prospecting,2014,49(1):22-34,46

[10]SPIKES K,DVORKIN J,MAVKO G.Rock physics model-based seismic inversion[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006:1645-1649

[12]印兴耀,张世鑫,张峰.双相介质理论指导下的流体因子精细构建与应用[J].地球物理学进展,2013,28(6):2911-2918

YIN X Y,ZHANG S X,ZHANG F.Delicate construction of fluid factor and its application based on two-phase media theory[J].Progress in Geophysics,2013,28(6):2911-2918

[13]印兴耀,宗兆云,吴国忱.岩石物理驱动下地震流体识别研究[J].中国科学:地球科学,2015,45(1):8-21

YIN X Y,ZONG Z Y,WU G C.Research on seismic fluid identification driven by rock physics[J].Science China:Earth Sciences,2015,45(1):8-21

[14]巴晶,晏信飞,陈志勇,等.非均质天然气藏的岩石物理模型及含气饱和度反演[J].地球物理学报,2013,56(5):1696-1706

BA J,YAN X F,CHEN Z Y,et al.Rock physics model and gas saturation inversion for heterogeneous gas reservoirs[J].Chinese Journal of Geophysics,2013,56(5):1696-1706

[15]李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):608-615

LI H B,ZHANG J J,YAO F C.Inversion of effective pore aspect ratios for porous rocks and its applications[J].Chinese Journal of Geophysics,2013,56(2):608-615

[16]蔡涵鹏,贺振华,唐湘蓉,等.碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J].石油物探,2013,52(6):566-572

CAI H P,HE Z H,TANG X R,et al.Influence analysis of carbonate pore structure and calculation of equivalent pore structure parameters[J].Geophysical Prospecting for Petroleum,2013,52(6):566-572

[17]HILL R.The elastic behaviour of a crystalline aggregate[J].Proceedings of the Physical Society,1952,65(5):349-354

[18]KUMAZAWA M.The elastic constants of single-crystal orthopyroxene[J].Journal of Geophysical Research,1969,74(25):5973-5980

[19]MARION D.Acoustical,mechanical and transport properties of sediments and granular materials[D].USA:Stanford University,1990

[20]HASHIN Z,SHTRIKMAN S.A variational approach to the theory of the elastic behavior of multiphase materials[J].Journal of the Mechanics and Physics of Solids,1963,11(2):127-140

[21]BERRYMAN J G.Mixture theories for rock properties[M]∥Ahrens T J.AGU Handbook of Physical Constants.Holland:Elseveier,1995:205-228

[22]孙晟,牛滨华,李佳.Hashin-Shtrikman弹性模量边界的转换[J].中国石油大学学报(自然科学版),2007,31(2):45-50

SUN S,NIU B H,LI J.Conversion of Hashin-Shtrikman elastic modulus bounds[J].Journal of China University of Petroleum(Edition of National Science),2007,31(2):45-50

[23]KUSTER G T,TOKSÖZ M N.Velocity and attenuation of seismic waves in two-phase media,part Ⅰ:theoretical formulations[J].Geophysics,1974,39(5):587-606

[24]KUSTER G T,TOKSÖZ M N.Velocity and attenuation of seismic waves in two-phase media,part Ⅱ:experimental results[J].Geophysics,1974,39(5):607-618

[25]BERRYMAN J G.Single-scattering approximations for coefficients in Biot’s equations of poroelasticity[J].Journal of the Acoustical Society of America,1992,91(2):551-571

[26]NORRIS A N.A differencial scheme for the effective moduli of composites [J].Mechanics of Materials,1985,4(1):1-16

[27]MUKERJI T,BERRYMAN J,MAVKO G,et al.Differential effective medium modeling of rock elastic moduli with critical porosity constraints[J].Geophysical Research Letters,1995,22(5):555-558

[28]ZIMMERMAN R W.Elastic moduli of a solid containing spherical inclusions[J].Mechanics of Materials,1991,12(1):17-24

[29]KEYS R G,XU S.An approximation for the Xu-White velocity model[J].Geophysics,2002,67(5):1406-1414

[30]BERRYMAN J G.Effective medium theories for multicomponent poroelastic composites[J].Journal of Engineering Mechanics,2006,132(5):519-531

[31]LI H B,ZHANG J J.Modulus ratio of dry rock based on differential effective-medium theory[J].Geophysics,2010,75(2):N43-N50

[32]LI H B,ZHANG J J.Analytical approximations of bulk and shear moduli for dry rock based on the differential effective medium theory[J].Geophysical Prospecting,2012,60(2):281-292

[33]李宏兵,张佳佳.多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J].地球物理学报,2014,57(10):3422-3430

LI H B,ZHANG J J.A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J].Chinese Journal of Geophysics,2014,57(10):3422-3430

[34]杨凤英,印兴耀,刘博.可变干岩石骨架等效模型研究[J].石油物探,2014,53(3):280-286

YANG F Y,YIN X Y,LIU B.The research of variable dry rock matrix equivalent model[J].Geophysical Prospecting for Petroleum,2014,53(3):280-286

[35]YANG F Y,YIN X Y,LIU B.S-wave velocity self-adaptive prediction based on a variable dry rock frame equivalent model[J].Journal of Geophysics and Engineering,2014,11(4):045015

[36]HILL R.A self-consistent mechanics of composite materials[J].Journal of the Mechanics and Physics of Solids,1965,13(4):213-222

[37]BUDIANSKY B.On the elastic moduli of some heterogeneous materials[J].Journal of the Mechanics and Physics of Solids,1965,13(4):223-227

[38]BERRYMAN J G.Long-wavelength propagation in composite elastic media Ⅰ:spherical inclusions [J].Journal of the Acoustical Society of America,1980,68(6):1801-1819

[39]BERRYMAN J G.Long-wavelength propagation in composite elastic media Ⅱ:ellipsoida inclusions [J].Journal of the Acoustical Society of America,1980,68(6):1820-1831

[40]WU T T.The effective of inclusion shape on the elastic moduli of a two-phase material[J].International Journal of Solids and Structures,1966,2(1):1-8

[41]WALSH J B.The effect of cracks on the uniaxial elastic compression of rocks[J].Journal of Geophysical Research,1965,70(2):399-411

[42]O’CONNELL R J,BUDIANSKY B.Seismic velocities in dry and saturated cracked solids[J].Journal of Geophysical Research,1974,79(B6):5412-5426

[43]HENYEY F S,POMPHREY N.Self-consistent elastic moduli of a cracked solid[J].Geophysical Research Letters,1982,9(8):903-906

[44]BERRYMAN J G.Mixture theories for rock properties,in a handbook of physical constants[M].Washington:American Geophysical Union,1995:205-228

[45]WOOD A W.A textbook of sound[M].New York:The MacMillan Co,1955:360

[46]WYLLIE M R J,GREGORY A R,GARDNER G H F.An experimental investigation of factors affecting elastic wave velocities in porous media[J].Geophysics,1958,23(3):459-493

[47]RAYMER L L,HUNT E R,GARDNER J S.An improved sonic transit time-to-porosity transform[J].Transactions of the SPWLA 21stAnnual Logging Symposium,1980,21(1):1-13

[48]ANGELERI G P,CARPI R.Porosity predication from seismic data[J].Geophysical Prospecting,1982,30(5):580-607

[49]KAMEL M H,MABROUK W M,BAYOUMI A I.Porosity estimation using a combination of Wyllie-Clemenceau equations in clean sand formation from acoustic logs[J].Journal of Petroleum Science & Engineering,2002,33(4):241-251

[50]GASSMANN F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4):673-685

[51]BIOT M A.Theory of propagation of elastic waves in fluid-saturated porous solid Ⅰ:low-frequency range[J].Journal of the Acoustical Society of America,1956,28(2):168-178

[52]BIOT M A.Theory of propagation of elastic waves in fluid-saturated porous solid Ⅱ:higher frequency range[J].Journal of the Acoustical Society of America,1956,28(2):179-191

[53]唐晓明.含孔隙、裂隙介质弹性波动的统一理论:Biot理论的推广[J].中国科学:地球科学,2011,41(6):784-795

TANG X M.A unified theory for elastic wave propagation through porous media containing cracks:an extension of Biot’s poroelastic wave theory[J].Science China:Earth Science,2011,41(6):784-795

[54]BROWN R J,KORRINGA J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid[J].Geophysics,1975,40(4):608-616

[55]MAVKO G,BANDYOPADHYAY K.Approximate fluid substitution for vertical velocities in weekly anisotropic VTI rocks[J].Geophysics,2009,74(1):D1-D6

[56]CIZ R,SHAPIRO S A.Generalization of Gassmann’s equations for porous media saturated with a solid material[J].Geophysics,2007,72(6):A75-A79

[57]GRECHKA V.Fluid-solid substitution in rocks with disconnected and partially connected porosity[J].Geophysics,2009,74(5):WB89-WB95

[58]王炳章.地震岩石物理学及其应用研究[D].成都:成都理工大学,2008

WANG B Z.Seismic rock physcis and its applied research[D].Chengdu:Chengdu University of Technology,2008

[59]HILL R.Elastic properties of reinforced solids:some theoretical principles[J].Journal of the Mechanics and Physics of Solids,1963,11(5):357-372

[60]HAN D H,NUR A,MORGAN D.Effects of porosity and clay content on wave velocities in sandstones[J].Geophysics,1986,51(11):2093-2107

[61]YAN X F,YAO F C,CAO H,et al.Analyzing the mid-low porosity sandstone dry frame in central Sichuan based on effective medium theory[J].Applied Geophysics,2011,8(3):163-170

[62]TOSAYA C A.Acoustical properties of clay bearing rocks[D].Stanford:Stanford University,1982

[63]EASTWOOD R L,CASTAGNA J P.Interpretation ofvP/vSratios from sonic logs[J].Geophysical Developments,1987:139-153

[64]KATAHARA K W.Clay mineral elastic properties[J].Expanded Abstracts of 66thAnnual Internat SEG Mtg,1996:1691-1694

[65]BERGE P A,BERRYMAN J G.Realizability of negative pore compressibility in poroelastic composites[J].Journal of Applied Mechanics,1995,62(2):1053-1062

[66]VANORIO T,PRASAD M,NUR A.Elastic properties of dry clay mineral aggregates,suspensions and sandstones[J].Geophysical Journal International,2003,155(1):319-326

[67]PRIDE S R.Relationships between seismic and hydrological properties[J].Hydrogeophysics,2005(50):253-290

[68]LEE W M.A simple method of predicting S-wave velocity[J].Geophysics,2006,71(6):161-164

[69]郭栋,印兴耀,吴国忱.横波速度计算方法与应用[J].石油地球物理勘探,2007,42(5):535-538

GUO D,YIN X Y,WU G C.The calculation method and application of transverse wave[J].Oil Geophysical Prospecting,2007,42(5):535-538

[70]邵才瑞,印兴耀,张福明,等.利用常规测井资料基于岩石物理和多矿物分析反演横波速度[J].地球科学:中国地质大学学报,2009,34(4):699-707

SHAO C R,YIN X Y,ZHANG F M,et al.Shear wave velocity inversion with routine well logs based on rock physics and multi-minerals nalysis[J].Earth Science-Journal of China University of Geosciences,2009,34(4):699-707

[71]张璐.基于岩石物理的地震储层预测方法应用研究[D].青岛:中国石油大学(华东),2009

ZHANG L.Application of rock physics theory in seismic reservior discrimination[D].Qingdao:China University of Petroleum,2009

[72]周中彪.基于岩石物理模型的测井约束横波速度计算方法研究[J].物探化探计算技术,2010,32(5):536-541

ZHOU Z B.The study on S-wave velocity calculation method constrained by logging based on rock physics models[J].Computing Techniques for Geophysical and Geochemical Exploration,2010,32(5):536-541

[73]熊晓军,林凯,贺振华.基于等效弹性模量反演的横波速度预测方法[J].石油地球物理勘探,2012,47(5):723-727

XIONG X J,LI K,HE Z H.Shear wave velocity prediction method based on equivalent elastic modulus inversion[J].Oil Geophysical Prospecting,2012,47(5):723-727

[74]王璞,吴国忱,李伟.基于改进模拟退火算法的横波速度求取[J].断块油气田,2015,22(3):330-333

WANG P,WU G C,LI W.Shear-wave velocity prediction based on revised and simulated annealing algorithm[J].Fault-Block Oil & Gas Field,2015,22(3):330-333

[75]张杨.利用Xu-White模型估算地震波速度[J].成都理工大学学报(自然科学版),2005,32(2):188-195

ZHANG Y.Xu-White model for seismic wave velocity prediction[J].Journal of Chengdu University of Technology (Science & Technology Edition),2005,32(2):188-195

[76]白俊雨,宋志翔,苏凌,等.基于Xu-White模型横波速度预测的误差分析[J].地球物理学报,2012,55(2):589-595

BAI J Y,SONG Z X,SU L,et al.Error analysis of shera-velocity prediction by the Xu-White model[J].Chinese Journal of Geophysics,2012,55(2):589-595

[77]印兴耀,李龙.基于岩石物理模型的纵、横波速度反演方法[J].石油物探,2015,54(3):249-253

YIN X Y,LI L.P-wave and S-wave velocities inversion based on rock physics model[J].Geophysical Prospecting for Petroleum,2015,54(3):249-253

[78]叶端南,印兴耀,王璞,等.砂泥岩储层岩石物理交会模板构建[J].地球物理学进展,2015,30(2):758-768

YE D N,YIN X Y,WANG P,et al.The build of rock physics cross plot template for sand shale reservoir[J].Progress in Geophysics,2015,30(2):758-768

[79]张繁昌,印兴耀.一种叠前地震记录的全波场正反演方法[J].石油物探,2004,43(3):217-222

ZHANG F C,YIN X Y.A full wave field forward modeling and inversion method for prestack seismogram[J].Geophysical Prospecting for Petroleum,2004,43(3):217-222

[80]SHARMA R,PRASAD M,SURVE G,et al.On the applicability of Gassmann model in carbonates[J].Expanded Abstracts of 76thAnnual Internat SEG Mtg,2006:1866-1870

[81]VEGA S,BERTEUSSEN K,SUN Y F,et al.Is Gassmann’ the best model for fluid substitution in heterogeneous carbonates?[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:1575-1578

[82]XU S,PAYNE M A.Modeling elastic properties in carbonate rocks[J].The Leading Edge,2009,28(1):66-74

[83]胡华锋,印兴耀,吴国忱.储层参数预测新方法:岩石物理模板技术[C]∥中国地球物理第二十六届年会论文集.宁波:中国地球物理学会,2010:570

HU H F,YIN X Y,WU G C.New method for reservoir parameters prediction-rock physics templates[C]∥ Abstracts of 26thAnnual Meeting of Chinese Geophysical Society.Ningbo,China:Chinese Geophysical Society,2010:570

[84]张广智,陈娇娇,陈怀震,等.基于岩石物理模版的碳酸盐岩含气储层定量解释[J].吉林大学学报:地球科学版,2015,45(2):630-638

ZHANG G Z,CHEN J J,CHEN H Z,et al.Quantitative interpretation of carbonate gas reservoir based on rock physics template[J].Journal of Jilin University (Earth Science Edition),2015,45(2):630-638

[85]ANSELMETTI F S,EBERLI G P.The velocity deviation log:a tool to predict pore type and permeability trends in carbonate drill holes from sonic and porosity or density logs[J].AAPG Bulletin,1999,83(3):450-466

[86]SAYERS C M.The elastic properties of carbonates[J].The Leading Edge,2008,27(8):1020-1024

[87]WEGER R J,BAECHLE G T,MASAFERRO J L,et al.Quantification of pore structure and its effect on sonic velocity and permeability in carbonates [J].AAPG Bulletin,2009,93(10):1297-1317

[88]LUCIA F J.Rock-fabric/petrophysical classification of carbonate pore space for reservoir characterization[J].AAPG Bulletin,1995,79(9):1275-1300

[89]包茨.天然气地质学[M].北京:科学出版社,1988:1-390

BAO C.Geology of natural gas[M].Beijing:Science Press,1988:1-390

[90]KAZATCHENKO E,MARKOV M,MOUSATOV A,et al.Joint inversion of conventional well logs for evaluation of double-porosity carbonate formations[J].Journal of Petroleum Science and Engineering,2007,56(4):252-266

[91]BAECHLE G T,COLPAERT A,EBERLI G P,et al.Modeling velocity in carbonates using a dual porosity DEM model[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:1589-1593

[92]KUMAR M,HAN D H.Pore shape effect on elastic properties of carbonate rocks[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005:1477-1480

[93]张广智,李呈呈,印兴耀,等.基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J].石油地球物理勘探,2012,47(5):717-722

ZHANG G Z,LI C C,YIN X Y,et al.A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J].Oil Geophysical Prospecting,2012,47(5):717-722

[94]吴志华,印兴耀.碳酸盐岩储层横波速度估算[C]∥SPG/SEG国际地球物理会议论文集.深圳:勘探地球物理学家学会,2011:56-59

WU Z H,YIN X Y.S-wave velocity prediction for carbonate reservoirs[C]∥Expanded Abstracts of SPG/SEG International Geophysical Conference.Shenzhen,China:Society of Exploration Geophysicists,2011:56-59

[95]王保丽,印兴耀,吴志华.各向异性碳酸盐岩储层精细横波速度估算方法[J].物探化探计算技术,2013,35(5):572-580

WANG B L,YIN X Y,WU Z H.High-resolution S-wave velocity evaluation method of anisotropy carbonate reservoir[J].Computing Techniques for Geophysical and Geochemical Exploration,2013,35(5):572-580

[96]陈怀震,印兴耀,张金强,等.基于方位各向异性弹性阻抗的裂缝岩石物理参数反演方法研究[J].地球物理学报,2014,57(10):3431-3441

CHEN H Z,YIN X Y,ZHANG J Q,et al.Seismic inversion for fracture rock physics parameters using azimuthally anisotropic elastic impedance[J].Chinese Journal of Geophysics,2014,57(10):3431-3441

[97]YIN X Y,LI C C,ZHANG G Z,et al.Estimation of S-wave velocity in carbonate rocks using the modified Xu-White model[J].Expanded Abstracts of 73rdEAGE Annual Conference,2011:23-26

[98]刘欣欣,印兴耀,张峰.一种碳酸盐岩储层横波速度估算方法[J].中国石油大学学报(自然科学版),2013,37(1):42-49

LIU X X,YIN X Y,ZHANG F.S-wave velocity estimation method in carbonate reservoir[J].Journal of China University of Petroleum (Edition of National Science),2013,37(1):42-49

[99]SMITH T M,SAYERS C M,SONDERGELD C H.Rock properties in low-porosity/low-permeability sandstones[J].The Leading Edge,2009,28(1):48-59

[100]EUGENIA R.Elastic rock properties of tight gas sandstones for reservoir characterization at Rulison Filed,Colorado[D].Colorado:Colorado School of Mines,2005

[101]RUIZ F,CHENG A.A rock physics model for tight gas sand[J].The Leading Edge,2010,29(12):1484-1489

[102]印兴耀,刘欣欣,曹丹平.基于Biot相洽理论的致密砂岩弹性参数计算方法[J].石油物探,2013,52(5):445-451

YIN X Y,LIU X X,CAO D P.Elastic parameters calculation for tight sand reservoir based on Biot-consistent theory[J].Geophysical Prospecting for Petroleum,2013,52(5):445-451

[103]李龙.碎屑岩致密储层岩石物理模量定量表征[D].山东青岛:中国石油大学(华东),2014

LI L.Quantitative characterization for rock physics modulus of tight clastic reservoir[D].Qingdao:China University of Petroleum,2014

[104]ROSS D J K,BUSTIN R M.Shale gas potential of the Lower Jurassic Gordondale Member northeastern British Columbia,Canada[J].Bulletin of Canadian Petroleum Geology,2007,55 (1):51-75

[105]VERNIK L,MILOVAC J.Rock physics of organic shales[J].The Leading Edge,2011,30(3):318-323

[106]VERNIK L,NUR A.Ultrasonic velocity and anisotropy of hydrocarbon source rocks[J].Geophysics,1992,57(5):727-735

[107]VERNIK L,LIU X.Velocity anisotropy in shales:a petrophysical study[J].Geophysics,1997,62(2):521-532

[108]HORNBY B E,SCHWARTZ L M,HUDSON J A.Anisotropic effective-medium modeling of the elastic properties of shales[J].Geophysics,1994,59(10):1570-1583

[109]BAYUK I O,AMMERMAN M,CHESNOKOV E M.Upscaling of elastic properties of anisotropic sedimentary rocks[J].Geophysical Journal International,2008,172(2):842-860

[110]COOPE D F,QUINN T H,FROST E F,et al.A rock model for shale gas and its application using magnetic resonance and conventional LWD logs[R].The Woodlands,Texas:SPWLA 50thAnnual Logging Symposium,2009

[111]SUN J,JIANG L,LIU X.Anisotropic effective-medium modeling of the elastic properties of shaly sandstones[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010:212-216

[112]VERNIK L,KHADEEVA Y,TUTTLE C.Rock physics of organic shale and its implication[R].Las Vegas,Nevada:Abstracts of GeoConvention,2012:1-7

[113]CARCIONE J,HELLE M H B,AVSETH P.Source-rock seismic velocity models:Gassmann versus Backus[J].Geophysics,2011,76(5):N37-N45

[114]ZHU Y,XU S,PAYNE M,et al.Improved rock-physics model for shale gas reservoirs [J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:4609-4614

[115]董宁,霍志周,孙赞东,等.泥页岩岩石物理建模研究[J].地球物理学报,2014,57(6):1990-1998

DONG N,HU Z Z,SUN Z D,et al.An investigation of a new rock physics model for shale[J].Chinese Journal of Geophysics,2014,57(6):1990-1998

[116]胡起,陈小宏,李景叶.基于各向异性岩石物理模型的页岩气储层横波速度预测[J].石油物探,2014,53(3):254-262

HU Q,CHEN X H,LI J Y.Shear wave velocity prediction for shale gas reservoirs based on anisotropic rock physics model[J].Geophysical Prospecting for Petroleum,2014,53(3):254-262

[117]张广智,陈娇娇,陈怀震,等.基于页岩岩石物理等效模型的地应力预测方法研究[J].地球物理学报,2015,58(6):2112-2122

ZHANG G Z,CHEN J J,CHEN H Z,et al.Prediction for in-situ formation stress of shale based on rock physics equivalent model[J].Chinese Journal

of Geophysics,2015,58(6):2112-2122

[118]郭小波,黄志龙,柳波,等.马朗凹陷芦草沟组泥页岩储层微观孔隙特征及地质意义[J].西北大学学报( 自然科学版),2014,44(1):88-95

GUO X B,HUANG Z L,LIU B,et al.Microscopic characteristics and geological significance of Lucaogou formation shale reservoir in Malang Sag[J].Journal of Northwest University (Natural Science Edition),2014,44(1):88-95

[119]BATZLE M,HOFMANN R,HAN D.Heavy oils-seismic properties[J].The Leading Edge,2006,25(6):750-756

[120]BEHURA J,BATZLE M,HOFMANN R,et al.Heavy oils:their shear story[J].Geophysics,2007,72(5):E175-E183

[121]HAN D H,YAO Q,ZHAO H Z.Complex properties of heavy oil sand[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:1609-1613

[122]HAN D H,ZHAO H Z,YAO Q.Velocity of heavy oil sand[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:1619-1623

[123]HAN D H,LIU J,BATZLE M.Seismic properties of heavy oils-measured data[J].The Leading Edge,2008,27(9):1108-1115

[124]GUREVICH B,OSYPOV K,CIZ R,et al.Modeling elastic wave velocities and attenuation in rocks saturated with heavy oil[J].Geophysics,2008,73(4):E115-E122

[125]DAS A,BATZLE M.Modeling studies of heavy oil-in between solid and fluid properties[J].The Leading Edge,2008,27(9):1116-1123

[126]DAS A,BATZLE M.A combined effective medium approach for modeling the viscoelastic properties of heavy oil reservoirs[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009:4338-4343

[127]MAKARYNSKA D,GUREVICH B,BEHURA J,et al.Fluid substitution in rocks saturated with viscoelastic fluids[J].Geophysics,2010,75(2):E115-E122

[128]吴志华.含流体孔隙介质岩石物理分析方法研究[D].山东青岛:中国石油大学(华东),2012

WU Z H.The study on rock physics analysis for porous media with fluid[D].Qingdao:China University of Petroleum,2012

(编辑：戴春秋)

Research status and progress of the seismic rock-physics modeling methods

YIN Xingyao1,2,LIU Xinxin3,4

(1.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China; 2.LaboratoryforMarineMineralResources,QingdaoNationalLaboratoryforMarineScienceandTechnology,Qingdao266071,China；3.TheKeyLaboratoryofMarineHydrocarbonResourcesandEnvironmentalGeology,MinistryofLandandResources,Qingdao266071,China; 4.QingdaoInstituteofMarineGeology,Qingdao266071,China)

Abstract:Rock-physics modeling is one of the most important parts in seismic rock physics research.Based on the two-phase media theory and the effective media theory,the theoretical framework of rock-physics modeling consists of four parts:rock matrix,rock frame,pore-filling material and the saturated rock.We discuss the assumed conditions and applicability of each fundamental rock physical model.Considering the lithology,microscopic pore structure and properties of pore-filling material of different reservoir types,including clastic,carbonate,tight sand,shale and heavy oil saturated reservoirs,we investigate the current situation and difficulties in rock-physics modeling,mainly discuss the more suitable modeling methods.Fully considering the rock microscopic characteristics and effectively use various types of data,seismic rock-physics models can be used to calculate the quantitative relationship between reservoir microscopic physical parameters and macroscopic elastic parameters,provide reliable foundations for reservoir quantitative interpretation and fluid identification.

Keywords:rock-physics model,effective media theory,pore structure,heterogeneous reservoir,elastic parameter,Xu-White model

收稿日期：2015-12-30;改回日期：2016-02-26。

作者简介：印兴耀(1962—),男,教授,博士生导师,现从事地球物理方法教学与研究工作。

基金项目：国家重点基础研究发展计划(973计划)课题(2013CB228604)、国家自然科学基金-石油化工基金联合重点项目(U1562215)共同资助。

中图分类号：P631

文献标识码：A

文章编号：1000-1441(2016)03-0309-17

DOI:10.3969/j.issn.1000-1441.2016.03.001

This research is financially supported by the National Key Basic Research and Development Program of China (973 Program) (Grant No.2013CB228604) and the National Natural Science Foundation of China (Grant No.U1562215).