基于优化灰色理论和神经网络的电力负荷短期预测
李娟(国网山东济南市历城区供电公司,济南 250101)
基于优化灰色理论和神经网络的电力负荷短期预测
李娟
(国网山东济南市历城区供电公司,济南250101)
摘要:为提高电力系统短期负荷的预测精度,确保电网安全和经济运行,提出一种基于优化的灰色理论和Elman神经网络混合方法。该方法充分考虑温度因素、周类型、天气状况等影响预测精度的不确定因素,通过数据模拟预测,该方法具有较高的预测精度和收敛速度,在电力系统短期负荷预测中具有一定的应用价值。
关键词:电力系统;负荷预测;灰色理论;Elman神经网络
0 引言
随着社会经济的发展,用户对电力负荷的要求越来越高,电力系统必须提供可靠持续并且具有良好质量的电能[1-2]。然而,电能的生产、输送、分配、消费是同时进行的,不能大量贮存,这就要求电力系统负荷预测的方法必须是科学有效的[3]。同时,电力系统短期负荷预测是电力系统中调度运营和用电服务部门日常的一项重要工作,也是电网规划决策的组成部分,是实现电网安全、经济运行的重要保障[4-5]。为了提高电网运行的稳定性、经济性和电力系统短期负荷预测精度,提出一种优化的灰色理论和Elman神经网络组合负荷预测方法,数据模拟仿真结果表明,该方法具有较高预测精度。
1 优化的灰色预测理论
1.1传统的灰色预测理论
灰色分析、灰色建模、灰色预测、灰色决策和控制是灰色系统理论主要研究的5个方面[6],该理论已广泛应用于电力、医学、军事等科学研究领域[7-8]。
在电力系统短期负荷预测中得到广泛应用的传统灰色系统预测模型为GM(1,1)。设x(0)为原始数据序列变量,则x(1)为生成的新的累加数列,则即
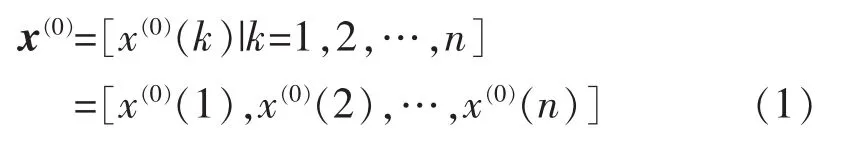


根据式(3)知,

式中:x(0)(k)为模型的灰导数;a为模型的发展系数;z(0)(k)为白色背景值;b为灰作用量。
将k=2,3,…,n代入式(4),得

引入矩阵,有
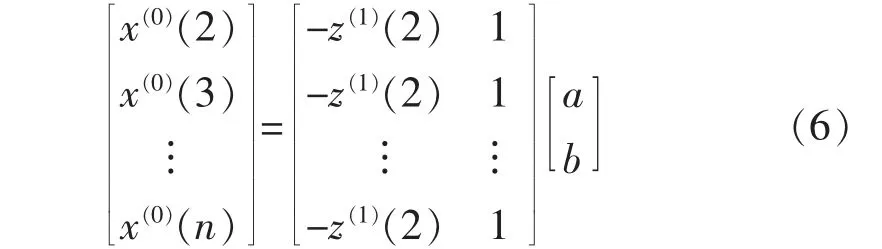
式(6)记为Y=Bu。
由最小二乘法,得a、b的值:

得预测值
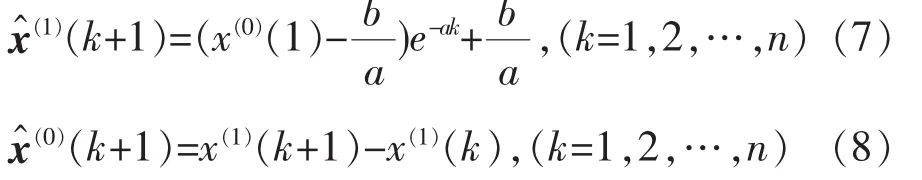
1.2优化的灰色预测模型
通过文献[9-10]得知模型GM(1,1)在应用中的局限性主要有以下两个方面。
1)GM(1,1)模型的精度随着发展系数的增大而精度越差;
2)在GM(1,1)模型中,具有真正意义的预测值是x(0)(n)后的第一、第二预测值,在最后面的预测值只能反映系统发展趋势。
为了克服上面的缺陷,提高预测精准度,达到较好的预测效果,必须对灰色预测技术进行优化。改进负荷预测技术的途径有多种,方式也各不相同,既可以通过改造原始数列、选取初值的方法改进输入端,也可以通过改进模型或改进技术的方法改进应用技术等。选用滑动平均法对原始数据进行改造,数据滑动平均法的具体步骤如下。
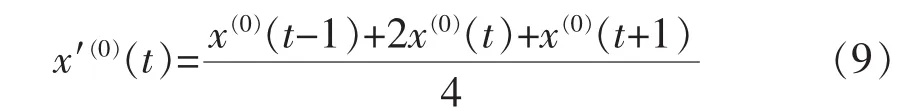
从式(9)可看出,不仅数据的权重增加,也避免了数值过度波动。
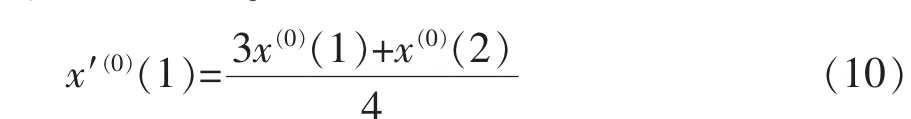
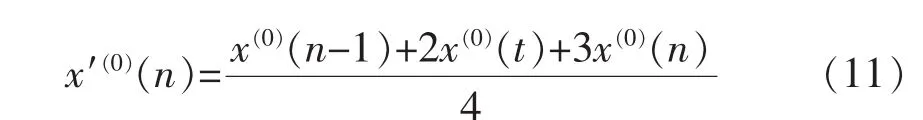
式(10)和(11)可以计算两端点值。
2 Elman神经网络
Elman神经网络属反馈型神经网络,由于该模型在隐含层中添加了承接层作为时延算子来达到记忆目的,使其对历史数据具有较强的敏感性[11]。
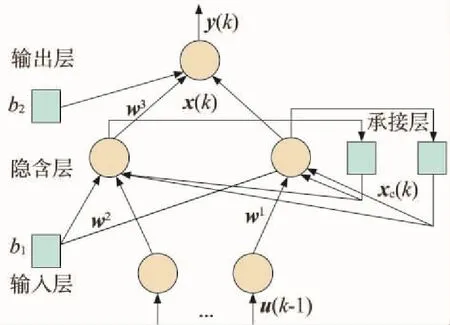
图1 Elman网络结构
输入层、输出层、隐含层和承接层4层组成了Elman神经网络结构,如图1所示。输入层主要用来传输信号和接收外部网络信息;输出层主要是用来输出网络计算结果同时起线性加权作用[12];线性函数或阈值函数、S型函数等非线性函数可为隐含层的传递函数;在这4层中,起承上启下作用的是承接层,我们可以认为它是一个一步延时算子,主要是用来记忆隐含层单元前一时刻的输出值并返回给网络的输入[13-14]。
由图1,可得Elman网络空间的关系表达式[15-16]:

式中:k为时刻节点向量;y为m维输出节点向量;x 为m维隐含层节点单元向量;u为n维输入向量;xc为m维反馈状态向量;w3、w2、w1表示层与层之间的连接权值矩阵;b1为输入层的阈值;b2为隐含层的阈值。这里选用tansig函数为f(.)为隐含层神经元的传递函数,purelin函数为g(.)为输出层神经元的传递函数[17]。
设第k步系统的实际输出向量为yd(k),在时间段内(0,T),则误差函数为
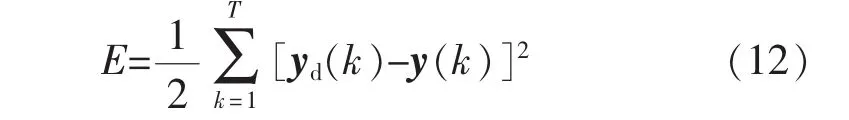
以w3、w2为例,求权值修正公式,需E对w3、w2分别求偏导,得

式中:η为学习速率;mc为动量因子。
3 模型建立及仿真
3.1选取输入、输出及隐含层节点
Elman神经网络的历史负荷输入节点由负荷时段的周期性原则来确定的。
模型建立。设L(n,t),t=0,1,…,23为输出变量;之前7天的对应预测时段的历史负荷数据用网络的输入变量L(n-i,t),i=1,2,…7;t=0,1,…,23来表示并添加最小温度值。一天中某个时段的负荷预测值用输出层来表示,对应一天中的24 h,这就要求进行运算的神经网络设置24个循环。
通过采用逐步确认的方式,选取了13个隐含层个数。
3.2样本数据归一化及选择网络参数
3.2.1样本数据归一化
历史负荷数据归一化。历史负荷数据进行归一化采用了最大最小值方法,即
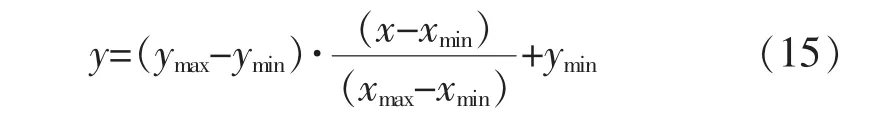
取y∈[-1,1],得

式中:x为负荷值;ymax、ymin分别为归一化后的最大、最小值;xmax为负荷最最大值;xmin为负荷最小值。
最小温度数据归一化。采用归一化的函数S型函数对温度数据进行归一化

式中:α为S型函数的偏值;β为形状系数。取α=20℃,β=13℃。
3.2.2选择网络参数
采用tansig函数和purelin函数作为Elman神经网络的隐含层的传递函数和输出层的传递函数,采用SSE作为网络输出误差计算式;取初始数率为0.7。得速率公式:

为了避免网络陷入到局部最小的困境,需在连接权系数中添加一个动量因子α,α的初始取值一般取0.95左右。即

3.3典型实例仿真
3.3.1算法流程
为了说明优化的灰色理论和Elman神经网络混合电力系统短期负荷进行数值模拟预测仿真。
1)读入初始化负荷数据和影响因素数据(包括天气情况、温度、风力等),迭代次数i=24。
2)进行数据预处理。用灰色预测算法实现电力负荷数方法的有效性,采用上述建立的模型和MATLAB软件对据缺失值的填补使用,用优化的灰色预测算法中的滑动平均法对异常数据进行修正。
3)用灰色关联分析,求取相关影响因素的关联度。确定最佳影响因素。
4)确定Elman各层神经元个数,将最佳影响因素添加到Elman神经网络的输入中。
5)对历史负荷数据和影响因素进行归一化,并进行Elman神经网络的电力系统短期负荷预测。
6)某个时段若i≤24,则转入7),否则进入9)。
7)对一天中的某个时段i进行负荷预测,得到该时间段的负荷预测值,时间段i=i+1,同时转入6)和8)。
8)得到并输出24个时段的负荷预测值和预测值与实际值的相对误差,转入9)。
9)流程结束。
3.3.2仿真结果
用上述的混合算法,对济南历城区2014年12月的历史负荷数据的负荷预测进行了数值模拟,结果如表1。模拟预测中综合考虑了不确定因素,如温
度、天气、周类型等。首先以经过灰色预测和优化方法进行修正后的历史负荷数据为基础,在不考虑其他影响因素的情况下进行Elman神经网络电力系统短期负荷预测;其次将最小温度影响因素添加到
Elman神经网络输入端,进行电力负荷预测。

表1 负荷预测模拟数值比较
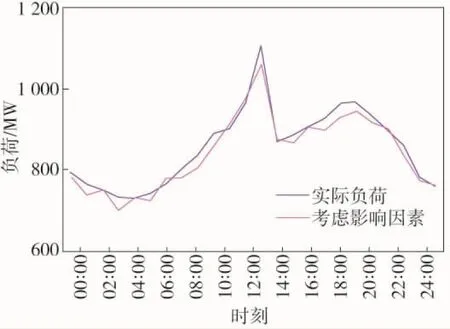
图2为未考虑影响因素的负荷预测拟合图。从表1可以计算出,经过优化的灰色预测以及Elman神经网络方法的平均相对误差为1.19%。从表1和图2可以得出预测结果趋近于实测值,具有很高的预测精度和收敛速度,结果令人满意。
图3为算法的负荷预测拟合图。从表1可以计算出该方法的平均相对误差为0.95%。从表1和图3可以看出在充分考虑了影响因素的情况下,结果比没有添加影响因素的情形还要精确,而且给出的算法收敛速度更快,整个结果还是相当令人满意的。

图2 未考虑影响因素的负荷预测拟合
4 结语
采用一种优化的灰色理论和Elman神经网络混合方法对电力系统短期负荷预测进行了研究。结果表明,该方法预测精度高,收敛速度快。
虽然该方法在电力系统短期负荷预测中具有一定的应用价值,但还有待进一步研究和改进,以使改方法更趋于完善。
参考文献
[1]张黎.电力负荷预测方法的研究与实现[D].哈尔滨:东北林业大学,2006.
[2]黄珊.配电网规划的回归分析负荷预测方法研究[D].长沙:湖南大学,2010.
[3]戴文进,付小科.电力系统负荷预测[J].科技前沿与学术评论,2002,24(3):40-43.
[4]周德强.基于最小二乘法的GM(1,1)模型及在负荷预测中的应用[J].电力系统保护与控制,2011,39(1):100-103.
[5]祖哲,毕贵红,刘力,等.基于小波神经网络的电力系统短期负荷预测模型研究[J].计算机技术与发展,2012,22(10):237-241.
[6]王世超.电力需求侧管理数据采集与处理的研究[D].北京:燕山大学,2012.
[7]晏榆洋.基于灰色理论的奥运会奖牌预测[J].四川文理学院学报,2011,21(5):21-23.
[8]仵拨云,杜兴无,任洋.灰色理论模型在软基沉降预测应用中准确性探讨[J].北方交通,2012,(12);14-17.
[9]孟欣,李郁侠.基于数据融合算法优化的GM(1,1)负荷预测模型[J].西安理工大学学报,2012,28(4):449-452.
[10]芮执元,任丽娜,冯瑞成.基于Elman神经网络的甘肃电网负荷预测模型[J].现代电力,2007,24(2):26-29.
[11]张英建,朱正泽,郭彩守.基于Elman神经网络的浓相输送模糊控制系统[J].微计算机信息,2007,23(9):68-70.
[12]王世超.电力需求侧管理数据采集与处理的研究[D].北京:燕山大学,2012.
[13]李春华,李宁,史培军.基于Elman神经网络模型的我国农业受灾面积预测研究[J].灾害学,2006,21(3):1-4.
[14]GE Hongwe,QIAN Feng,LIANG Yanchun.Identification and control of nonlinear systems by a dissimilation particle swarm optimization-based Elman neural network[J].Nonlinear Analysis:Real World Applications,2008(9):1345-1360.
[15]郑唯唯,徐济超,杜涛.基于Elman网络的过程质量智能化控制研究[J].机械科学与技术,2007,26(1);41-44.
[16]陈振斌,张万红,彭勃.基于Elman神经网络的江苏技术人才需求预测[J].商场现代化,2007(12):12-15.
[17]HU Shixiao.Improved Elman Networks and Applications for Controlling Ultrasonic Motors[J].Applied Artificial Intelligence,2004,18(7):603-629.
Short Term Forecasting of Power Load Based on Optim ized Grey Theory and Neural Network
LI Juan
(State Grid Licheng Power Supply Company,Jinan 250101,China)
Abstract:In order to improve the accuracy of power system short term load forecasting and to ensure security and economy of power grid,a hybrid method based on improved gray theory and Elman neural network is proposed.This method takes into account some factors affecting the prediction accuracy,such as temperature,week type and the weather condition.It has been proved that the method has higher prediction accuracy and convergence rate through data simulation.It has certain application value in the short term load forecasting of the power system.
Key words:power system;power load forecasting;grey theory;Elman neural network
中图分类号:TM734
文献标志码:A
文章编号:1007-9904(2016)02-0031-05
收稿日期:2015-09-14
作者简介:
李娟(1982),女,工程师,从事电力系统相关工作。

