含光伏电源的配电网规划研究
辛 欣,张新慧,王 龙,咸日常,孙桂花(.山东理工大学电气与电子工程学院,山东 淄博 55049;.国网山东省电力公司淄博供电公司,山东 淄博 55000)
含光伏电源的配电网规划研究
辛欣1,张新慧1,王龙2,咸日常1,孙桂花1
(1.山东理工大学电气与电子工程学院,山东淄博255049;2.国网山东省电力公司淄博供电公司,山东淄博255000)
摘要:考虑光伏电源接入电网后出力的随机性,采用随机期望值的规划模型,建立了以年费用最小为目标的含光伏电源配电网规划模型,并运用改进的自适应遗传算法模型求解,获得光伏电源的最优接入位置及容量规划。自适应遗传算法克服了传统遗传算法易于陷入局部最优的缺点,通过算例验证,证明了模型及算法的可行性。
关键词:光伏电源;配电网规划;随机性;自适应遗传算法
(2012AA050213);山东省高等学校科技计划项目(J14LN27)
0 引言
随着能源短缺、环境污染等问题的日益突出,人们将目光更多地转向新兴能源,光伏发电就是其中一种。其凭借能源的取之不尽、安全性高、设计灵活、噪声污染小等优点,发展迅速。受光照波动性影响,光伏电源具有明显的波动性,对电力系统的正常运行产生影响,影响程度与光伏发电的接入位置与容量密切相关。因此,选择光伏电源的接入位置与容量变得非常重要[1-2]。
目前,针对含分布式电源的配电网问题国内外学者提出了许多不同的方法,并得到了验证,但只针对光伏电源规划问题研究的较少。文献[3]以网络年费用最小为优化目标,并考虑了停电损失,运用遗传算法求解出规划方案。文献[4]建立了规划模型,考虑了电压偏移及分布式电源数量容量的限制,并用多目标非线性规划问题求解方法进行求解。文献[5]在建立的规划模型中考虑了建设费用,网损费用及购电费用,但没有考虑分布式电源政策补贴成本。上述文献大多是将分布式电源当作一种模型处理,没有考虑到光伏电源的随机出力问题。
从光伏电源的投资建设角度出发,考虑光伏电源出力及负荷变动的随机性,建立光伏电源投资运行费用、网损费用、购电费用、补贴费用等组成目标函数模型,运用遗传算法对光伏电源的位置、容量进行优化,规划含光伏电源的配电网。
1 含光伏电源的配电网规划模型
配电网规划数学模型是在满足运行要求的条件下对规划方案经济性进行评价的标准,主要包括目标函数和约束条件两部分。
1.1目标函数
该规划模型以年费用最小为目标,其中包括光伏电源的年投资和运行费用,线路的年运行费用,购电费用和光伏电源发电的补贴费用。目标函数为
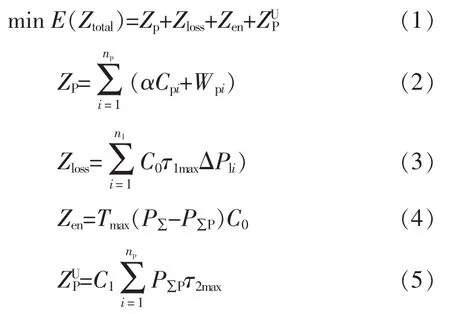
式中:Ztotal为年费用的期望值;Zp为光伏电源的年投资运行及维护成本的期望值;Zloss为网络年损耗费用的期望值;Zen为向上级电网的购电费用的期望值;ZUP为光伏电源政策补贴节省的社会成本的期望值;np为接入配电网的光伏电源个数;α为光伏电源的运行维护费用系数;Cpi为第i个光伏电源的投资费用,万元;Wpi为第i个光伏电源的运行维护费用;n1为配电网线路个数;C0为单位电价,元/kWh;τ1max为第i条支路的年最大负荷损耗小时数;ΔPli为第i条支路上的有功损耗,万kW;Tmax为最大负荷年利用小时数;P为配电网总有功功率;PP为分布式电源总有功出力;C1为因光伏发电节约的单位环境成本,元/kWh;τ2max为年最大光照利用小时数。
1.2约束条件
不等式约束条件包括节点电压的约束,支路功率的约束以及光伏电源容量的限制。
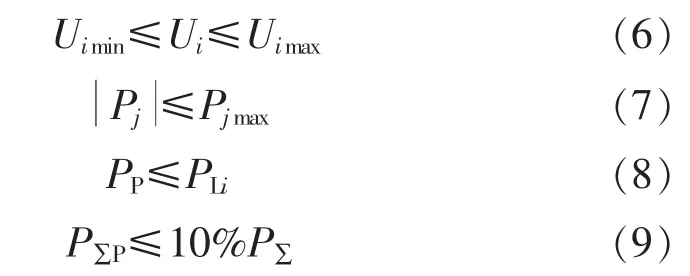
式中:Ui为节点电压;Ui max、Ui min分别为节点电压的上、下限;Pj为流过j支路上的有功功率;Pjmax为j线路的容量传输极限;PP为配电网中允许的最大接入容量。
由于光伏电源受光照、温度等条件的影响,其出力具有不稳定性,考虑到系统要具有稳定性,需要对光伏电源的容量加以限制。在约束条件里对光伏电源容量做出限制,即式(9),负荷点上的光伏电源容量不要超过所在节点负荷的大小,光伏电源按总最大接入容量不超过电网最大负荷总量的10%[6,11]。
2 随机因素的处理
2.1光伏电源的随机模型
光伏电源的出力与光照强度有直接关系,光照强度受地域,季节以及天气因素的影响,光照强度的随机性决定了光伏电源输出功率的随机性。根据统计一段时间内光照强度的概率密度[6]为

式中:α和β为Beta分布的形状参数;r为时间段内某时刻光照强度;rmax则为时间段内的光照强度最大值。
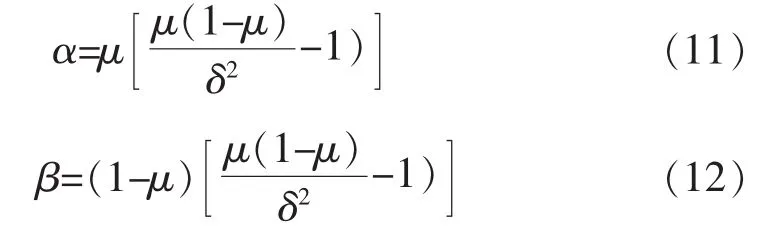
式中:μ和δ分别为光照强度期望和方差。
光伏系统输出的有功功率[8]可以表示为

式中:k为逆变器的效率;r为光照强度;A为光伏电源电池阵列的面积;η为光伏电源的光电转换效率。
将式(13)代入式(10),可以得到光伏电源输出功率的概率密度函数
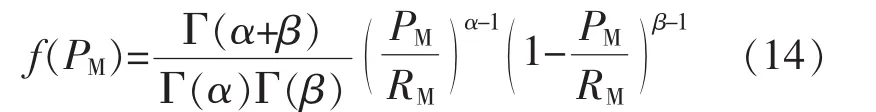
2.2负荷的随机模型
配电网的各负荷节点也存在随机性,经过长期研究,发现可以利用正态分布来反映负荷的随机性[7],节点有功和无功概率分布
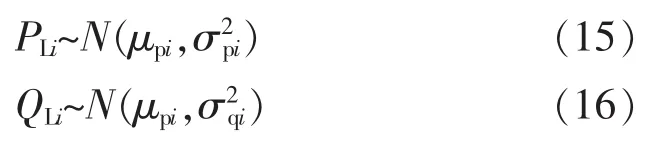
式中:μpi为有功期望值;σ2pi为有功方差;μqi为无功期望值;σ2qi为无功方差。
3 求解策略
采用自适应遗传算法对光伏电源的布点及容量进行规划。遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索方法,它通过模拟自然过程来搜索最优解[9]。遗传算法通过选择、交叉、变异3个基本操作来实现寻找到最优解的目的。交叉概率Pc和变异概率Pm的选择就影响遗传算法的性能,自适应遗传算法中Pc、Pm能够随适应度自动的改变,保证遗传算法的收敛性。
3.1染色体编码
实数编码是遗传算法的一种重要编码方式。对光伏电源位置和容量变量采用实数编码的方式,规定光伏电源的接入位置在负荷节点上,且每个负荷节点最多接入一个光伏电源。变量组C={C1,C2,…,Cn}说明光伏电源的建设情况,如Ci=0表示在负荷节点i上不安装光伏电源,如Ci=1则表示在负荷节点i上安装容量为50 kW的光伏电源。
3.2光伏电源位置和容量初始群体的产生
初始群体是随机产生的,但随机产生的初始群体往往不能满足约束条件中光伏电源容量的限制,这样就不可避免地出现许多不可行解,如果使用这些不可行解继续迭代计算,会影响收敛速度以及搜索范围,甚至造成无解,所以要对初始群体进行检验和修正[10]。首先计算出配电网最大负荷总量,确定光伏电源接入容量的上限,然后随机产生一个群体,对该初始群体中个体进行校验,保证各节点的光伏电源容量小于该节点的负荷量,所有个体容量和小于式(9)中计算出的负荷总量,如果符合此要求,则该群体作为初始群体;如果不符合要求,则重新产生群体,直到满足要求。
3.3约束问题的解决
优化问题含不等式约束,处理这种问题一般采用罚函数法,就是把所有约束问题化为无约束问题,再用无约束问题的方法求解。罚函数是将惩罚项加入适应度函数中,降低不可行解的适应度。采用以下形式将罚函数包含到适应度评价中:
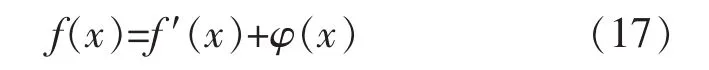
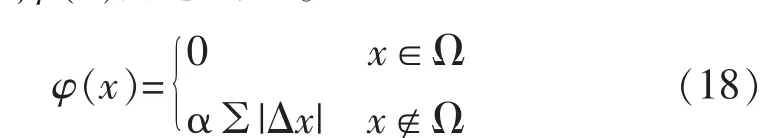
式中:f(x)为原有目标函数;f′(x)为加入惩罚函数后的目标函数;φ(x)为惩罚项。式中:α为惩罚尺度系数;Δx为基因值的越界量;Ω为可行解空间。目标函数加入惩罚项后得到的新目标函数为

3.4适应度函数
遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群中每个个体的适应值来进行搜索。上文中,已将约束条件通过惩罚函数转化为无约束条件,形成了新的目标函数。适应度是由目标函数变换而成的。对于目标函数为最小问题,适应度函数采用以下形式:式中:f′(x)为目标函数;Cmax为f′(x)的最大值估计。
3.5遗传操作

遗传算法的基本操作步骤包括3项:选择、交叉和变异。从初始群体开始,适应度函数作为依据,通过上述3项基本操作,不断地进化繁衍,实现结构重组,最后收敛到最适应的个体,从而得到问题的最优解。
选择算子大约有15种形式,特点各不相同,本文选择最优保存策略,其特点是能够保证全局收敛,其方法是适应度最高的个体不参与交叉及变异运算,而是用它来替换适应度低的个体,这样保证了最优个体的适应度不低于前代群体的适应度。
自适应遗传算法是一种交叉概率和变异概率都随适应度改变而自动改变的算法。当种群各个个体适应度趋于一致或者区域局部最优时,使Pc和Pm增加,而当群体适应度比较分散时,使Pc和Pm减少。这样使算法中的Pc和Pm值能够维持在最佳值,群体在保持多样性的同时,也保证了遗传算法的收敛性。自适应遗传算法中,Pc和Pm计算表达式为
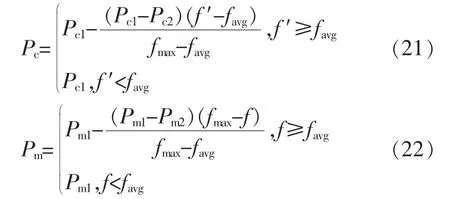
式中:fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;Pc1取值为0.9;Pc2取值为0.6;Pm1取值为0.1;Pm2取值为0.001。
3.6搜索终止条件
遗传算法是一种随机进行的搜索方法,找到一个标准的收敛判别条件非常困难。常用的终止条件有3种,一是前后两代群体适应度之差小于事先设定的整数,二是达到最优解连续不变的最大代数,三是采用达到预先设定的代数即终止,选择第三种作为搜索终止条件。
算法实现流程如图1所示。

图1 含光伏电源的配电网规划流程
4 算例分析
按照上述规划模型及求解算法,在MATLAB环境下,对IEEE33节点配电网系统进行算例的分析计算,如图2所示,此配电网是由33个节点,32条支路构成的辐射型网络,其基准电压为12.66 kV,总有功负荷为3 715 kW,总无功负荷为2 300 k v ar,1~32节点均可接入光伏电源。

图2 IEEE 33节点配电网系统
算例中参数的选取:光伏电源年费用系数α=0.06,投资建设费用为18 000元/kW,运行维护费用为130元/kW,年最大负荷利用小时数及年负荷最大损耗小时数年都取3 000 h,最大光照利用小时数取α、β1 500 h,单位电价为0.5元/kWh,国家补贴成本为0.42元/kWh。光伏电源的随机出力模型中α=0.9,β= 0.85。种群的大小M取60,最优解连续不变的最大代数为5,迭代终止次数取50。规划结果如表1所示。对光伏电源接入前后的费用、网损和电压比较,如表2~3所示。

表1 光伏电源安装位置和容量的规划结果
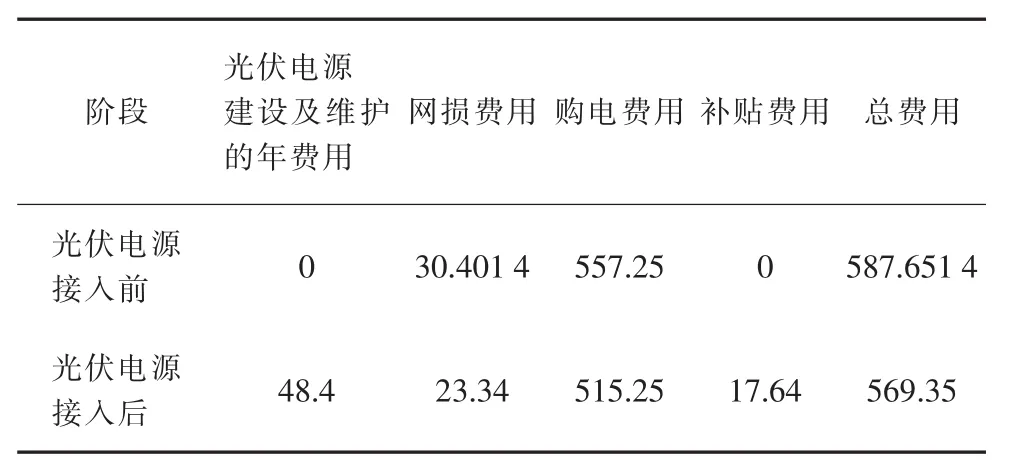
表2 光伏电源接入前后费用对比 万元

表3 光伏电源接入前后网损及电压对比
表2可以看出接入光伏电源后总费用减少了3%,网损费用较少了23.2%,购电费用减少了7.5%。从规划结果来看,光伏电源的接入位置都偏向配电网线路的末端,这是因为接入末端能更加有效地减少系统网损,提高系统的电压,增强配电网的带负载能力。表3给出的是规划前后的有功网损及最低节点电压的对比情况,光伏电源的接入使配电网的有功网损减少了47.076 kW。接入前,节点17电压最低,为0.913 pu,接入光伏电源后,节点32电压最小,为0.930 pu,光伏电源对于提高系统电压有明显的作用。
5 结语
随着新能源的发展,光伏电源会更多地接入配电网系统。光伏电源经济、安全及合理的接入对配电网的运行有重要意义。从经济性角度出发,以年费用最小为规划目标,考虑光伏电源输出功率的随机性,采用自适应的遗传算法进行求解,并通过IEEE33节点系统算例验证了模型及算法的可行性,为含光伏电源的配电网规划提供了一种有效的方法。
参考文献
[1]美国国际太阳能协会.太阳能光伏发电设计与安装指南[M].湖南:湖南科技技术出版社,2014.
[2]熊伟.含多个光伏电源的微电网规划[D].长沙:中南大学,2011.
[3]郭贤,郭贺,程浩忠,等.考虑用户停电损失的微网网架规划[J].电工技术学报,2014,29(8):301-307.
[4]KIM K H,LEE Y J,RHEE S B,et al.Dispersed generator placement sing fuzzy-GA in distribution systems[C]∥Proc.2002 IEEE Power Eingeering Society.Summer Meeting,2002,3:1 148-1 153.
[5]李娜,李永刚,李建文.含分布式电源的配电网扩展规划研究[J].电测与仪表,2014,51(8):32-37.
[6]KARAKI S H,CHEDID R B,RAMADAN R.Prohah Wttc Performance Assessment of Autonomous Solar-wind Energy Converston System[J].IEEE Trans on Energy Conversion,1999,14 (3):766-772.
[7]CHARYTONIUK W,CHEN M S,KOTAS P,et al.Demand forecasting in power distribution system using nonparametric probability density estimation[J].IEEE Transaction on Power Systems,1999,14(4):1200-1206.
[8]樊磊.分布式光伏电源并网出力概率分布模型的研究[D].北京:华北电力大学,2012.
[9]熊信银,吴耀武.遗传算法及其在电力系统中的应用[M].武汉:华中科技大学出版社,2002.
[10]蔡丽霞.含分布式电源的配电网规划研究[D].济南:山东大学,2009.
[11]CELLI G,PILO F.Optimal Distributed Generation Allocation in MV Distribution Network.Proceedings of 22nd IEEE Power Engineering society International conference on Power Industry Computer Applications.Sydney(Australia),2001:81-86.
Study of Distribution Network Planning w ith Photovoltaic Power
XIN Xin1,ZHANG Xinhui1,WANG Long2,XIAN Richang1,SUN Guihua1
(1.School of Electrical and Electronic Engineering,Shandong University of Technology,Zibo 255049,China;2.State Grid Zibo Power Supply Company,Zibo 255000,China)
Abstract:Considering randomness of the output of the photovoltaic power when it is accessed to power network.The distribution network planning model with photovoltaic power was built according to the planning model of random expectations.The goal of the model was minimum total investment costs.During the solving process,the modified adaptive genetic algorithm was used to get the optimal access location and capacity planning of photovoltaic power.Furthermore,the algorithm can avoid calculation falling into local optimum.Finally the correctness and feasibility of the model and the algorithm were proved by an example.
Key words:photovoltaic power;distribution network planning;randomness;improved adaptive genetic algorithm
中图分类号:TM72
文献标志码:A
文章编号:1007-9904(2016)02-0001-04
基金项目:国家高技术研究发展计划(863计划)资助项目
收稿日期:2015-10-22
作者简介:
辛欣(1990),女,硕士研究生,主要从事配电网规划方向的研究。

