交流电压不对称下柔性直流配网换流站功率传输极限研究

杨 峰，徐习东，裘愉涛

(1.浙江大学, 浙江 杭州 310027；2.浙江省电力公司，浙江 杭州 310007)

交流电压不对称下柔性直流配网换流站功率传输极限研究

杨 峰1，徐习东1，裘愉涛2

(1.浙江大学, 浙江 杭州 310027；2.浙江省电力公司，浙江 杭州 310007)

为了维持直流配网中直流电压的稳定，需要换流器在交流电压不对称时消除传输功率的二倍频波动。分析了交流电压不对称下换流器的不平衡控制策略。由于换流器过流能力限制，换流站的传输功率极限受不对称电压影响，推导了交流侧传输功率极限解析式。针对直流侧功率极限解析式难以求得的问题，提出了直流侧功率极限的数值计算方法。最后通过电磁暂态仿真软件 PSCAD/EMTDC 对交流电网不对称下换流器传输功率极限进行了验证。功率极限值的给定，为合理分配多端直流配电网各端的功率，维持直流电压稳定提供了参考。

功率传输极限；交流电压不对称；柔性直流配网；电压源换流器；不平衡控制

0 引言

柔 性 直 流 配网 是基 于 电压 源换 流 器(Voltage Source Converter，VSC)的新兴配网技术[1-6]。柔性直流配网运行过程中，交流电压不对称情况时有发生。当交流电网发生不对称故障或交流配网因负载不对称导致交流电压不对称时，换流站交流侧电压将包含负序分量，不经控制，会引起直流侧电压和功率的二倍频(100 Hz)波动[7]。直流配网的优点之一是可以隔离交流侧故障对直流侧的影响，为此需要设计电压源换流器的不平衡控制策略[8-15]。这些控制策略以消除功率波动、维持直流电压稳定为目标，其核心是间接电流控制[16]，即利用瞬时功率理论计算出一组正、负序电流参考值，控制换流器在不平衡条件下跟踪输出这组电流来消除瞬时功率中的波动分量，达到稳定直流电压的目的。

然而，换流器的过流能力有限，当交流系统负序分量较大时，上述控制器一旦受过流能力限制，将无法准确跟踪参考电流，导致输出功率波动。实际上当系统发生相间金属性故障时，换流器不能无波动地传输任何有功功率[17]。考虑更一般的交流电压不对称情况，换流器能够传输的有功功率存在一个极限值，该值与电网电压不对称情况及过流限值存在复杂的关系。

为此，本文分析了已有的不平衡控制策略，考虑 VSC 过流能力的限制，研究了不同的交流不对称条件下，换流站的交直流两侧功率输出极限值。只要控制换流器传输功率低于该极限值，就可以消除交流侧不对称电压对直流侧的影响，为合理分配交直流混合配电网中各换流站功率，维持直流电压的稳定提供了参考。

1 交流电压不对称下 VSC 功率控制

1.1 功率分析

VSC换流站系统拓扑结构如图1所示，其中R和L表示交流侧等效电阻和换流电感，C表示直流侧电容，表示换流站交流系统电压，表示换流站交流出口侧电压，表示直流电压。

图1 VSC 换流站拓扑结构Fig. 1 Topological structure of VSC

根据文献[8-11]推导，交流电压不对称情况下的系统侧和换流电抗上的功率组成如式(1)和式(2)所示。

1.2 不平衡控制策略

由于电流控制的维度限制，通常在设计 VSC 控制器时只控制(1)式中的其具体表达式为

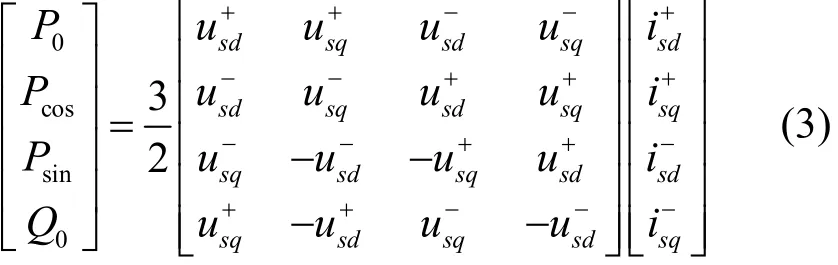
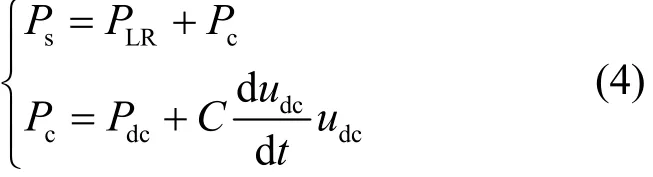
式中：Ps为交流系统总功率；为等效换流阻抗上消耗的功率；为交流侧传输到换流器的功率，若不考虑换流器损耗，等于换流器传输到直流侧的功率；为直流负载功率。由式(4)可知，在稳定的直流负荷条件下，为了维持直流电压的稳定，需保证无波动。

交流系统不对称时，VSC的不平衡控制通常采用正负序分离的双闭环控制结构，其基本思想如图2所示。

图2 VSC 不平衡控制策略Fig. 2 Unbalanced control strategy of VSC

首先根据控制需要设计外环控制器，若电压矩阵可逆，则按式(5)计算出消除波动所需的参考电流指令值组合。然后将这组电流指令作为内环电流控制器的输入，最后结合换流器数学模型产生触发脉冲控制换流器交流侧出口电压，实现各自控制目标。

图2中外环控制器用来控制有功、无功或者直流电压，如图3 所示，其输出为和的参考值。功率中的波动相和的参考值给定有 2 种情况：若不考虑换流阻抗上的波动，则两者都设为0；若考虑环流阻抗，则将其设为换流阻抗上的波动量和

内环电流控制包括线性控制和非线性控制，其中以双矢量电流控制(Dual vector current control, DVCC)最为常用，它包含 PI控制器、交叉解耦和电压前馈控制，能实现同步旋转坐标系下 dq轴电气量解耦，同时在消除控制其中二次谐波分量的影响上效果明显，本文在仿真建模时采用这种内环控制器。

图3 不平衡控制的外环控制器Fig. 3 Outer loop controllers of unbalanced control

1.3 不平衡控制中的功率波动控制

由(3)可得电压矩阵的行列式为

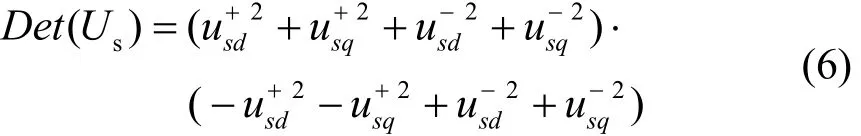
由式(6)可知，当负序电压幅值等于正序电压幅值时，行列式的值为 0，式(3)中电压矩阵不可逆，要使波动相和为零，则必须令功率指令也为零，即此时无法输出无波动的功率。

当三相对称系统发生带过渡电阻的相间短路，负序电压幅值接近正序电压时，式(3)中电压矩阵可逆，其逆矩阵中存在大数值的元素，若要保证交流侧电流不越限，同时使波动相和为零，则式必须小于某个特定值。后文从交流侧电流分析入手，探讨的极限值。

2 电网不对称时的交流侧电流分析

2.1 不平衡控制下交流电流幅值表达式推导

由于电力电子器件过载能力有限，换流器对实际流过 VSC 的三相电流幅值有限流要求。为此，需对交流电流幅值的表达式进行推导。为简化模型假设：

(1) 忽略交流侧电压与电流的谐波分量；

(2) VSC 通常经隔离变压器接入交流系统，不对称故障引起的交流电压零序量可由变压器接线方式隔离[18]，因此 VSC 交流侧只存在电流与电压的正、负序分量；

根据假设，不对称的三相交流电压和经不平衡控制后输出的三相交流电流瞬时值可表示为

式(7)和式(8)分别按式(10)和式(11)进行坐标变换得到同步旋转坐标系下的四个电流值

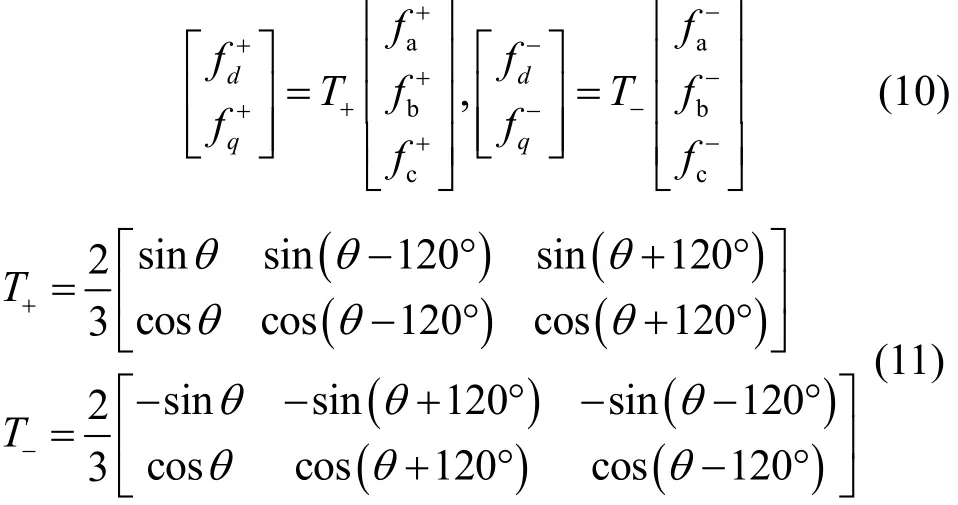
在变量变换过程中为了保证锁相不受负序电压带来的影响，设计锁相环将相位锁定在A相正序基波电压，即式(11)中：

由式(5)和式(8)—式(11)可推得

2.2 交流不对称情况对交流电流幅值的影响分析

将式(14)代入式(13)得到式(15)。由式(15)可知，三相电流幅值与成线性关系，与成非线性关系。

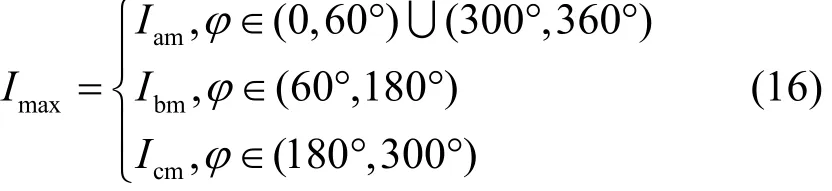
Fig. 4 Magnitude of the largest AC current with variound j

3 限流条件下的功率传输极限

3.1 交流侧功率极限

考虑到换流站的过流能力，实际的 VSC 交流侧输出电流将受到限制，反过来导致交流侧功率传输受限，即存在极限值。

由式(13)和式(17)得

式(18)即为考虑了换流器过流能力限制后，推得的换流器交流侧传输的功率极限与电压不对称条件的关系。

由前文交流电流曲面图可知，交流侧输出功率极限值同样都出现在j等于的情况。为了求出单个换流器的功率极限，取φ等于0，做交流系统功率极限值随和变化的曲面图，如图5 所示，其中正序电压幅值为 10 kV 时，系统额定功率为 10 MW，交流过流能力为 1.2 倍额定电流。

由图5可知，交流侧功率极限随不对称度增大而下降，随正序电压幅值下降而下降。当交流系统不对称度接近1时或正序电压很低的情况下，系统几乎不能无波动地输送任何有功功率。

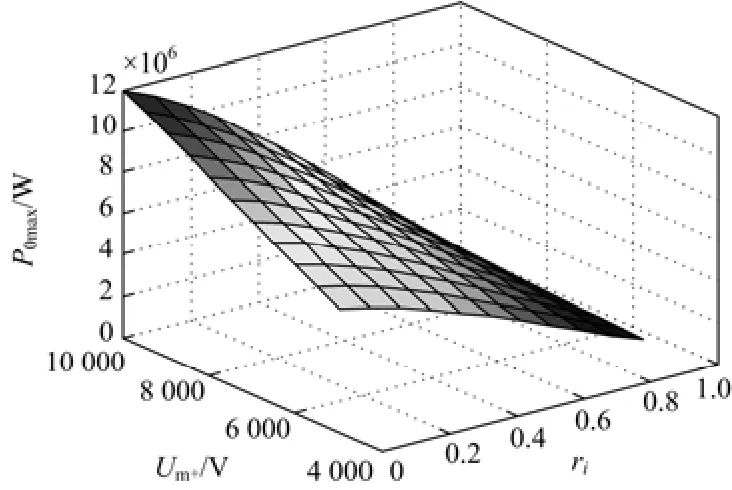
图5 换流器交流侧功率极限值随和变化曲线图Fig. 5 Transmission power limit of the AC side with variousand

3.2 直流侧功率极限计算

判别式1为

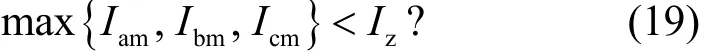
判别式2为

图6 交流电压不对称条件下直流侧功率极限的计算框图Fig. 6 Steps for calculating the transmission power limit of the DC side

图6 中步骤6为一个矩阵迭代计算电流参考值的过程，而迭代方法往往对初值敏感，初值选取偏离最终解有可能导致迭代结果发散或震荡。为解决这个问题，本文将式(18)计算得到的功率极限作为迭代计算的功率初值。

图7所示为按本文提出的步骤迭代计算得到的直流侧功率极限随正序电压幅值以及不对称度变化的曲面图，系统参数和过流条件与 3.1 节中图5 算例相同，换流电感 L=5.6 mH，等效电阻其中为考虑环流阻抗的功率极限值，表示的差，变化范围为 10~5 kV，变化范围为 0~0.9。

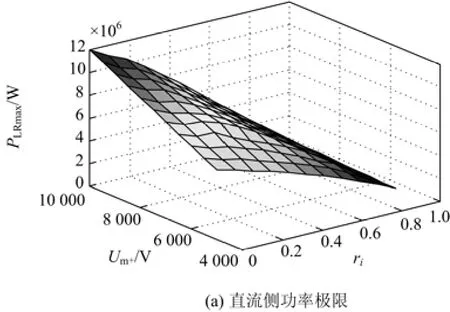
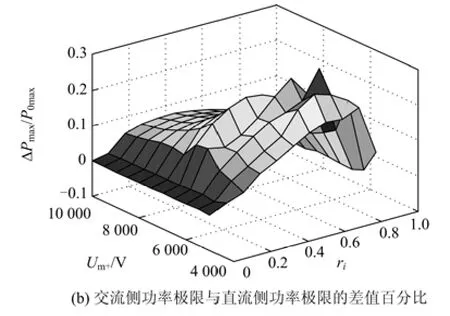
图7 直流侧功率极限与交流功率极限对比Fig. 7 Comparison between transmission power limit of the AC side and that of the DC side

由图7(a)可知，换流器直流侧传输功率极限值随不对称情况的变化趋势与交流侧功极限相同，均随不对称度增大而下降，随正序电压幅值下降而下降，当交流系统不对称度接近1时或正序电压很低时，系统几乎不能无波动地输送任何有功功率。由图7(b)可知，大多数不对称电压情况下，直流侧功率极限位于交流侧功率极限的上方，但也存在后者大于前者的情况。因此，当交流电压不对称时，为保证直流侧功率与电压稳定，需对换流器的功率进行限制，其极限值大小不能仅用式(18)求取，需要在此基础上进一步通过图6所示的迭代方法求得。

4 仿真验证

为验证所推导的不对称条件下三相电流幅值表达式的准确性，同时验证限流环节对交流功率传输与直流电压波动的影响，建立如图1 所示的 VSC 换流站系统，系统参数如表1所示。其中VSC换流器采用两电平结构，直流侧根据戴维南等效用串联的直流电压源与线路阻抗表示。利用电磁暂态仿真软件 PSCAD/EMTDC 对交流系统不平衡时的系统响应进行仿真。

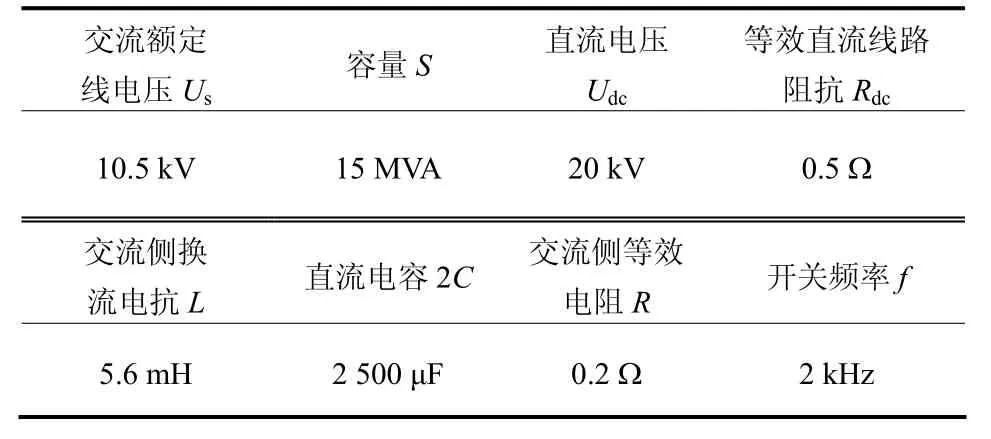
表1 VSC 换流站系统主要参数Table 1 Main parameters of VSC stations

4.1 交流侧功率控制

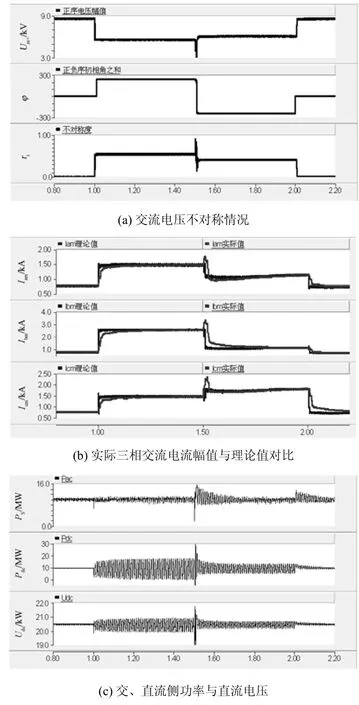
图8 定交流功率控制系统响应Fig. 8 System response with power control of the AC side

由图8(a)、图8(b)可知，根据交流系统三个不平衡条件计算得到的三相电流幅值的理论值与实际值的拟合度高，表明本文推导的电流幅值表达式的准确性。由图8(c)可知，交流不对称时，换流站控制能够将交流侧的波动消除，但由于换流电感 L上波动的存在，直流侧的功率与电压仍有波动。

4.2 直流侧功率控制

VSC 采用文献[8-10]中计及换流阻抗的不平衡控制策略，控制器以消除直流侧功率与电压波动为目标，外环功率指令仿真系统参数不变，仿真过程经历“不对称出现、引入限流控制、降功率运行”三个阶段，如 表2 所 示 。不 对 称 电 压 条 件为 ：交流侧单相限流值为 1.2 kA。

表2 仿真过程Table 2 Simulation process

VSC 系统响应的仿真结果如图9所示。

由图9 可知：1 s时交流电压出现不对称，VSC控制器起作用，虽然直流侧功率和电压波动得到消除，但此时单相电流超过限流值；1.1 s 时，限流环节起作用，三相电流过流情况消除，直流功率和电压出现波动；1.2 s 后，根据电压不对称条件，按本文提出的方法计算得到的功率极限值为 5.77 MW，因此有功指令下调至 5.50 MW 后运行是安全的，三相电流均不超过限流值，直流侧功率与电压波动被消除。

图9 定直流功率控制系统响应Fig. 9 System response with power control of the DC side

5 结论

交流侧出现不对称电压时，换流器需要通过不平衡控制来消除直流侧功率的二倍频波动以获得稳定的直流电压。在不平衡控制下，换流器的传输功率极限与换流器的过载能力以及交流侧不对称电压密切相关，本文对此进行了分析，推导了换流器交流侧传输功率极限与交流侧不对称电压的关系，提出了换流器直流侧功率极限的迭代计算方法，并在PSCAD/EMTDC 中进行了仿真验证，验证了上述推导结果和计算方法，同时得到以下结论：

(1) 当交流电压不对称时，换流器交流侧的无波动功率极限可以通过推导求得，而直流侧的功率极限可以通过数值计算的方法迭代求得。

(2) 在不同的不对称电压情况下，换流器交流侧无波动功率极限与直流侧无波动功率极限不完全相等，他们的差值不总小于0。

(3) 在换流器交流侧存在负序电压的情况下，为确保直流侧功率无波动，必须使换流器的实际功率小于对应电压与限流条件下的直流侧功率极限值。

[1]朱童, 赵宇明, 余占清, 等. 中压柔性直流配电系统故障暂态仿真研究[J]. 高压电器, 2015, 51(11): 26-32. ZHU Tong, ZHAO Yuming, YU Zhanqing, et al. Fault transient simulation of middle-voltage MMC-HVDC distribution system[J]. High Voltage Apparatus, 2015, 51(11): 26-32.

[2]崔福博, 郭剑波, 荆平, 等. 直流配电技术综述(英文)[J]. 电网技术, 2014, 38(3): 556-564. CUI Fubo, GUO Jianbo, JING Ping, et al. A review of DC power distribution technology[J]. Power System Technology, 2014, 38(3): 556-564.

[3]周逢权, 黄伟. 直流配电网系统关键技术探讨[J]. 电力系统保护与控制, 2014, 42(22): 62-67. ZHOU Fengquan, HUANG Wei. Study on the key technology of DC distribution power network[J]. Power System Protection and Control, 2014, 42(22): 62-67.

[4]MANSOUR T, AMIRNASER Y. A DC distribution system for power system integration of plug-in hybrid electric vehicles[C]// Power and Energy Society General Meeting (PES), 2013: 1-5.

[5]VEKHANDE V, FERNANDES B G. Bidirectional currentfed converter for integration of DC micro-grid with ac grid[C]// 2011 Annual IEEE India Conference (INDICON), 2011: 1-5.

[6]姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 中国电机工程学报, 2013, 33(36): 27-33. YAO Zhiqing, YU Fei, ZHAO Qian, et al. RT-LAB based modeling and simulation analysis of flexible DCdistribution network[J]. Proceedings of the CSEE, 2015, 33(36): 27-33.

[7]陈海荣. 交流系统故障时 VSC-HVDC 系统的控制与保护策略研究[D]. 杭州: 浙江大学, 2007. CHEN Hairong. Control and protection of VSC based HVDC system under AC system fault conditions[D]. Hangzhou: Zhejiang University, 2007.

[8]姜卫东, 吴志清, 佘阳阳, 等. 电网不平衡时抑制有功功率二次波动的并网逆变器控制策略[J]. 电力系统自动化, 2014, 38(15): 106-111. JIANG Weidong, WU Zhiqing, SHE Yangyang, et al. Control strategy of suppressing active power secondary fluctuations of grid-connected inverter based on unbalanced grid[J]. Automation of Electric Power Systems, 2014, 38(15): 106-111.

[9]阳同光, 桂卫华. 电网不平衡情况下并网逆变器控制策略综述[J]. 电工技术学报, 2015, 30(14): 241-246. YANG Tongguang, GUI Weihua. An overview on control strategies of grid-connected inverter under unbalanced voltage conditions[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 241-246.

[10]朱鑫, 刘俊勇, 刘洋, 等. 基于滑模变结构的含不平衡负荷微电网控制策略研究[J]. 电力系统保护与控制, 2015, 43(6): 25-32. ZHU Xin, LIU Junyong, LIU Yang, et al. Study of microgrid control strategy contained unbalanced load based on sliding-mode variable structure[J]. Power System Protection and Control, 2015, 43(6): 25-32.

[11]高航, 苏建徽, 汪晶晶, 等. 模块化多电平型换流器电容电压二倍频波动抑制策略研究[J]. 电力系统保护与控制, 2014, 42(6): 116-122. GAO Hang, SU Jianhui, WANG Jingjing, et al. Study on control strategy for suppressing double fundamental frequency fluctuation of capacitor voltage of modular multilevel converter[J]. Power System Protection and Control, 2014, 42(6): 116-122.

[12]XU L, ANDERSEN B R, CARTWRIGHT P. VSC Transmission operating under unbalanced AC conditions— analysis and control design[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 427-434.

[13]ETXEBERRIA O I, VISCARRET U, CABALLERO M, et al. New optimized PWM VSC control structures and strategies under unbalanced voltage transients[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2902-2914.

[14]LEON A E, MAURICIO J M, SOLSONA J A. Adaptive control strategy for VSC-based systems under unbalanced network conditions[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 311-319.

[15]翦志强, 司徒琴. 三相电压不对称跌落光伏并网逆变器控制方法[J]. 电力系统保护与控制, 2015, 43(14): 126-130. JIAN Zhiqiang, SITU Qin. Control method of photovoltaic grid-connected inverter under three-phase voltage unbalanced dips[J]. Power System Protection and Control, 2015, 43(14): 126-130.

[16]吴奎华, 李玉玲, 林平, 等. 基于间接电流控制的电流型 PWM 整流器[J]. 电力系统及其自动化学报, 2008, 20(3): 62-65. WU Kuihua, LI Yuling, LIN Ping, et al. Current source PWM rectifier based on indirect current control[J]. Proceedings of the CSU-EPSA, 2008, 20(3): 62-65.

[17]SACCOMANDO G, SVENSSON J. Transient operation of grid-connected voltage source converter under unbalanced voltage conditions[C]// 2001 IEEE Industry Applications Conference, 2001: 2419-2424.

[18]易 桂 平 , 胡 仁 杰 , 蒋 玮 , 等 . 电 网 电 压 不 平 衡 对STATCOM 的影响及抑制 [J]. 电工技术学报, 2014, 29(6): 238-247. YI Guiping, HU Renjie, JIANG Wei, et al. Influence of grid voltage unbalance on STATCOM and the countermeasure[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 238-247.

[19]MAGUEED F A, SVENSSON J. Control of VSC connected to the grid through LCL-filter to achieve balanced currents[C]// 2005 Industry Applications Conference, 2005: 572-578.

[20]唐欣, 李建霖, 滕本科. 提高扰动下 VSC-HVDC 供电电压质量的逆变站控制方法[J]. 电工技术学报, 2013, 28(9): 112-119. TANG Xin, LI Jianlin, TENG Benke. Enhancement of voltage quality in a passive network supplied by a VSC-HVDC system under disturbances[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 112-119.

(编辑 姜新丽)

Research on transmission power limit of flexible DC distribution converters under unbalanced AC voltages

YANG Feng1, XU Xidong1, QIU Yutao2
(1. Zhejiang University, Hangzhou 310027, China; 2. Zhejiang Electric Power Corporation, Hangzhou 310007, China)

To stabilize the DC voltage in a DC distribution network, it is necessary to suppress the double fundamental frequency fluctuation of the active power under unbalanced AC voltages. This paper analyzes unbalanced control strategies of voltage source converters (VSCs). Due to the overcurrent capability of converters, the transmission power limit of VSCs varies with various unbalanced AC voltage conditions. The transmission power limit of the AC side is deduced. Then a numerical method is put forward to calculate the transmission power limit of the DC side. Examples of power transmission under unbalanced AC voltages are simulated by electromagnetic transient simulation software PSCAD/EMTDC. The transmission power limits of VSCs of both the AC and DC sides are necessary for power distribution in multi-terminal DC distribution network. To suppress the fluctuation of the DC voltage, it is necessary to control the active power of VSCs within the transmission power limit of the DC side.

This work is supported by National High-tech R & D Program of China (863 Program) (No. 2015AA050104).

transmission power limit; unbalanced AC voltages; flexible DC distribution; voltage source converter (VSC); unbalanced control

10.7667/PSPC151800

：2015-12-07

杨 峰(1990-)，男，通信作者，硕士研究生，研究方向为柔性直流配网不平衡控制；E-mail: 373965909@qq.com

徐习东(1966-)，男，博士，副教授，研究方向为电力系统继电保护,柔性直流配网控制；E-mail: xxd@zju.edu.cn

裘愉涛(1967-)，男，硕士，高级工程师，从事继电保护技术管理工作。

国家 863 高技术基金项目(2015AA050104)