基于直觉模糊推理的直觉模糊时间序列模型
王亚男, 雷英杰, 王 毅, 范晓诗
(空军工程大学防空反导学院, 陕西 西安 710051)
基于直觉模糊推理的直觉模糊时间序列模型
王亚男, 雷英杰, 王毅, 范晓诗
(空军工程大学防空反导学院, 陕西 西安 710051)
摘要:由于受到模糊集理论的限制,模糊时间序列预测理论在不确定数据集的描述上有失客观,针对这种局限性,提出一种直觉模糊时间序列预测模型。应用模糊聚类算法实现论域的非等分划分;针对直觉模糊时间序列的数据特性,提出一种更具客观性的隶属度和非隶属度函数的确定方法;提出一种基于直觉模糊近似推理的模型预测规则。在Alabama大学入学人数和中国社会消费品零售总额数据集两组数据集上分别与典型方法进行对比实验,结果表明该模型有效提高了预测精度,证明了模型的有效性和优越性。
关键词:直觉模糊时间序列; 模糊聚类; 隶属度函数; 非隶属度函数; 直觉模糊推理
0引言
时间序列预测无论在经济领域(如国民收入、股票指数),社会领域(如客运流量、学校入学人数)还是自然领域(如温度、降水量)都有着广泛而重要的应用。传统的时间序列预测方法主要是以ARIMA模型为代表的基于统计分析的方法,这类方法存在两大弊端:第一,需要大量历史数据且历史数据需满足诸多限制;第二,不能预测历史数据为语言值或历史数据不完整、不准确的问题。因此,文献[1]利用模糊集能够描述和处理模糊信息的优势,借助模糊逻辑理论,首次提出了模糊时间序列(fuzzy time series, FTS)的概念,并在Alabama大学入学人数数据集上进行了实验验证。
模糊时间序列预测的基本思想是用模糊集表示历史数据,用模糊关系表示序列的动态变化趋势,在历史数据不精确或不完整的情况下,利用模糊推理得到理想的预测结果。由于其在不确定性数据处理上的优势,模糊时间序列理论在面世的短短20年间就受到了广泛关注,并取得了大量有价值的研究成果:文献[2]针对历史数据及其概率均为模糊集的情况,建立了一个模糊随机模糊时间序列模型;文献[3]首次系统地讨论了如何确定论域划分的有效长度,提出基于分布和基于平均的两种划分方法;文献[4-5]将信息粒理论引入论域划分,提出一种有效的非等分划分方法;文献[6]考虑了模糊关系出现的频率,采用与文献[2]不同的加权0-1矩阵表示模糊逻辑关系;文献[7-8]提出几个高阶模型分别运用优化算法、人工神经网络等对模型进行改进;文献[9]用模糊关系的重要性取代出现频率作为权重的依据,并据此提出一种新的去模糊化方法;文献[10]将模糊关系分为递增、不变和递减3类,根据各自概率进行多元高阶模糊时间序列的预测。FTS模型中对历史数据模糊化时采用了传统的Zadeh模糊集概念,即只用一个属性——隶属度来度量语言值的模糊性质,既不够全面也不够客观,极大地影响了FTS模型处理不确定信息的能力,限制了模型预测精度的提升。
考虑到直觉模糊集(intuitionistic fuzzy sets, IFS)用隶属度、非隶属度和直觉指数3个指标来描述信息的模糊性,较传统模糊集更加客观和细腻,文献[11]首次将直觉模糊集理论融入时间序列分析,建立了一个直觉模糊推理系统进行数据的预测,但其本质还是基于两个隶属度模糊推理系统和非隶属度模糊推理系统的加权合成。文献[12]在FTS模型的基础上初步建立了直觉模糊时间序列(intuitionistic fuzzy time series, IFTS)预测模型,但其直觉模糊隶属度函数和非隶属函数的构造方法存在一定的缺陷,导致隶属度和非隶属度之和的最大值恒为0.8。文献[13-14]利用直觉模糊C均值聚类方法实现论域的自动非等分划分,并且在预测步骤中引入回溯机制和矢量预测技术有效提高了预测精度,但如何有效地直觉模糊化历史数据,使其符合直觉模糊C均值的应用条件,成为模型实现有效预测的一大限制。直觉模糊集理论的引入极大地扩展了时间序列对不确定、不完备等模糊信息的处理能力,为模糊时间序列研究开辟了新的研究方向。然而,当前IFTS理论的研究仅崭露头角,国内外相关学术成果很少,且仅有的理论研究缺乏标准化的定义和模型,理论深度不够,预测精度有待进一步提高。
鉴于以上问题,本文从论域划分、直觉模糊集建立和预测规则3个方面入手对模型进行优化改进,建立了一个基于直觉模糊推理的IFTS模型。通过在通用数据集上的实例计算,验证所建模型有效克服了FTS模型的缺陷,取得了较好的预测结果。
1基本概念
定义 1设X是一给定论域,则X上的一个直觉模糊集A为
(1)
式中,μA(x):X→[0,1]和γA(x):X→[0,1]分别代表A的隶属函数和非隶属函数,且对于A上的所有x∈X,0≤μA(x)+γA(x)≤1成立。称πA(x)=1-μA(x)-γA(x)为x的直觉指数,它是x对A的犹豫程度的一种测度。
定义 2设X和Y是普通有限非空集合或论域。定义在直积空间X×Y上的直觉模糊子集R为从X到Y之间的二元直觉模糊关系。记为
(2)
式中,μR(x,y):X×Y→[0,1]和γR(x,y):X×Y→[0,1]满足条件0≤μR(x,y)+γR(x,y)≤1, ∀(x,y)∈X×Y。
定义 3设给定论域X(t)(t=1,2,…)为R的一个子集,fi(t)=〈μi(X(t)),γi(X(t))〉(i=1,2,…)为定义在X(t)上的直觉模糊集,若F(t)={f1(t),f2(t),…},则称F(t)为定义在X(t)上的直觉模糊时间序列。
这里,F(t)表示语言变量,fi(t)表示可能的语言变量值,例如若F(t)为语言变量“年龄”,则fi(t)可以是“较老”“年老”“较年轻”“年轻”“年幼”等。因为F(t)的取值随时间t而变化,故F(t)为t的函数,且论域也随t而变化,所以常将X(t)看作变化的论域。
定义 4设R(t,t-1)为从F(t-1)到F(t)之间的直觉模糊关系,且F(t)是由F(t-1)通过直觉模糊关系R(t,t-1)推导得到的,即
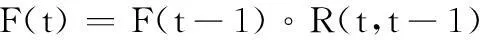
(3)
式中,“∘”表示直觉模糊合成运算,则称R(t,t-1)为F(t)上的一阶直觉模糊逻辑关系。
定义 5如果对于任意的t,R(t,t-1)均与t无关,即

(4)
则称F(t)为时不变直觉模糊时间序列;否则,称其为时变直觉模糊时间序列。
本文研究对象为一阶时不变直觉模糊时间序列。
2基于直觉模糊推理的IFTS模型
与FTS类似,IFTS预测模型可以概括为以下4个步骤:
步骤 1根据历史数据确定论域大小,并对论域进行划分;
步骤 2建立直觉模糊集,并直觉模糊化历史数据;
步骤 3建立预测规则,求得预测值;
步骤 4预测结果去模糊化输出。
接下来按照步骤1~步骤4建立本文模型。
2.1基于模糊聚类的非等分论域划分
首先,定义问题的讨论范围,即论域U=[xmin-ε1,xmax+ε2],其中xmin和xmax分别表示历史数据的最小值和最大值;ε1和ε2是两个合适的正数,为了讨论和计算上的方便使得xmin和xmax分别向下、向上取合适的整数。
然后,划分论域。论域划分的理论和规律在FTS模型和IFTS模型上是通用的,文献[3,6]的研究已表明,在FTS模型中使用非等分划分方法会产生比等分方法更好的预测结果,近年来很多学者采用遗传算法、粒子群算法和FCM等算法来实现非等分的论域划分,这类算法的每个子区间具有明显实际意义,更符合人们的理解习惯。但是,这类算法通常在大数据条件下才能充分发挥其优良性能,这又与FTS和IFTS模型不需要大量历史数据的优势相背离;此外,预测方法在实际中也多用于数据量不大的经济、环境等问题。因此,本文采取了较遗传算法等优化算法更简捷更具实时性的基于最大生成树的直接模糊聚类算法[5]。
设X={x1,x2,…,xn}是待分类对象的全体,其中xi=(xi1,xi2,…,xim),i=1,2,…,n,即xi有m维特征。所谓最大树法就是以被分类对象为顶点,相似矩阵R的元素rij为边的权重而得到的一棵最大树,然后取定阈值λ∈[0,1],去掉权重小于λ的边,得到一个不连通的图,其中各连通分支的顶点便构成了一个在λ水平上的分类。对于不同的λ可以得到不同的分类,从而得到一组动态分类,因此算法的最后还需确定一个最佳阈值λ从而对应一个最优分类,确定最佳阈值的方法有F统计量方法等。文献[15]对算法具体步骤已有详细介绍,本文不再赘述。
聚类得到的r类数据可记为

记
(5)
则论域U被划分成r个不等长的区间:
2.2直觉模糊集的建立
对应于论域U的r个区间,定义r个代表语言变量的直觉模糊集
(6)
确定Ai的隶属度和非隶属度函数是该步骤的关键所在。由于直觉指数的影响,确定直觉模糊集的隶属度和非隶属度函数的方法呈现极大的复杂性。已有方法如模糊统计法、三分法、二元对比排序法等多将直觉指数固定为一个常数[16],有失客观性,因此本节针对IFTS模型实际应用情况和划分区间的特性,给出以下方法。
首先,通过客观分析,给出以下两条规则:
(2) 当x位于区间边界即x=di时,直觉指数取最大值,隶属度和非隶属度相等,根据具体情况令πAi(di)=α, 0≤α≤1,则
根据上述规则,隶属度函数采用典型Gaussian函数
(7)
非隶属度函数由Gaussian函数变形得到
(8)
则直觉指数函数为
(9)
式中,i=1,2,…,r,cμi、σμi和cγi、σγi为函数的参数,是确定隶属度和非隶属函数的关键,依然由上述规则计算得到
(10)
(11)
(12)
定义 6A为有限论域X上的直觉模糊集,如果A满足:
(1) 0≤μA(x)≤1,0≤γA(x)≤1;
(2) 0≤πA≤1,0≤μA(x)+γA(x)≤1;
(3) μA(x)+γA(x)+πA(x)=1。
则称直觉模糊集A为正规直觉模糊集。
根据该定义,可得以下定理:
定理 1本节提出的隶属度、非隶属度和直觉指数函数的确定方法是规范的,即Ai是正规直觉模糊集。
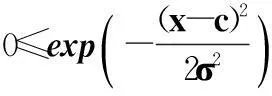
进而得0≤πAi(x)=1-μAi(x)-γAi(x)≤1。
(3) 由直觉指数函数的确定方法,明显可得μAi(x)+γAi(x)+πAi(x)=1。
证毕
定理1从理论上证明本文隶属度函数和非隶属度函数的确定方法是正确、规范、合理的。
2.3基于直觉模糊推理的预测规则
2.3.1直觉模糊多重取式推理
设Ai(i=1,2,…,n)和A*是U上的直觉模糊集,Bi和B*是V上的直觉模糊集,基于直觉模糊关系的广义多重取式推理规则陈述的是:给定n+1个直觉模糊命题“x是A*”和 “如果x是Ai,则y是Bi”,可推出一个新的直觉模糊命题 “y是B*”,推理模型[17]为

规则:IF x is A1THENy is B1IF x is A2THENy is B2︙IF x is AnTHENy is Bn输入:IF x is A*输出:y is B*
对于每一条规则可以得到一个输入输出关系Ri,在此使用Mamdani蕴涵算子Rc。运用不同的算子,可得到不同的μR与γR,所以计算结果的数值不唯一,而推理输出的结果基本是一致的。在直觉模糊推理中,Rc性能较好且便于计算,因此选取Rc进行推理计算[16]。
(13)
式中
(14)
(15)
从而由直觉模糊规则的合成运算可得总的直觉模糊关系R为
(16)
式中
(17)
(18)
推理输出为
(19)
式中,直觉模糊合成运算“∘”采用取大“∨”、取小“∧”运算,即
(20)
(21)
2.3.2IFTS模型的预测规则
受直觉模糊多重取式推理的启发,将IFTS中的序列数据与代表语言变量的直觉模糊集Ai(i=1,2,…,r)的地位互换,即将序列数据看作直觉模糊集,记为Fj(j=1,2,…,t),将Ai看作集合的元素,μAi(x)与γAi(x)看作元素Ai对集合Fj的隶属度和非隶属度,则直觉模糊集Fj可表示为
(22)
式中
(23)
(24)
则对Fj和Ai运用多重取式推理,可得推理模型为

规则:IF x is F1THENy is F2IF x is F2THENy is F3︙IF x is FjTHENy is Fj+1︙ IF x is Ft-1THENy is Ft输入:IF x is Ft输出:y is F*t+1
推理输出为
(25)
式中
(26)
(27)
则
(28)
(29)
2.4解模糊算法
直觉模糊集的解模糊算法通常有重心法、加权平均法和最大真值法等,由于重心法具有比较平滑的输出控制,及对应于输入信号的微小变化输出也会发生一定的变化,且这种变化明显比较平滑,因此本节采用重心法对推理结果解模糊化[17]。重心法的具体计算方法是取隶属度函数和非隶属度函数合成的真值函数曲线与横坐标围成的平面图像面积的重心为解模糊的输出值,即
(30)
式中,U为输出论域;F为定义在论域U上的直觉模糊子集。
3模型应用
3.1Alabama大学数据集实验
Alabama大学从1971-1992年的招生人数数据是Song等首次提出FTS模型是使用的一组数据,此后研究FTS模型的学者常将该数据集作为模型的测试集。应用本文的IFTS模型在该数据集上进行实验,具体步骤如下:
步骤 1定义论域并划分。
以1971-1991年的招生人数为历史数据,预测1992年的招生人数,历史数据中xmin=13 055,xmax=19 337,通常定义论域U=[13 000,20 000]。
按照第2.1节方法将论域U划分为9个区间,为便于计算将所有数据均缩小1 000倍。
u1=[13.000,13.309], u2=[13.309,14.282]
u3=[14.282,14.921], u4=[14.921,16.186]
u5=[16.186,16.598], u6=[16.598,17.535]
u7=[17.535,18.560], u8=[18.560,19.149]
u9=[19.149,20.000]
步骤 2建立直觉模糊集,直觉模糊化历史数据。
对应论域U的9个区间建立9个直觉模糊集A1,A2,…,A9,它们的现实意义可以理解为:“很少”“少”“较少”“微少”“正常”“微多”“较多”“多”“很多”。接下来按照第2.3节的方法确定个直觉模糊集的隶属度和非隶属函数,令α=0.4,各参数的值如表1所示。

表1 隶属度和非隶属度函数参数值
各直觉模糊集的隶属度函数、非隶属度函数和直觉指数如图1~图3所示。
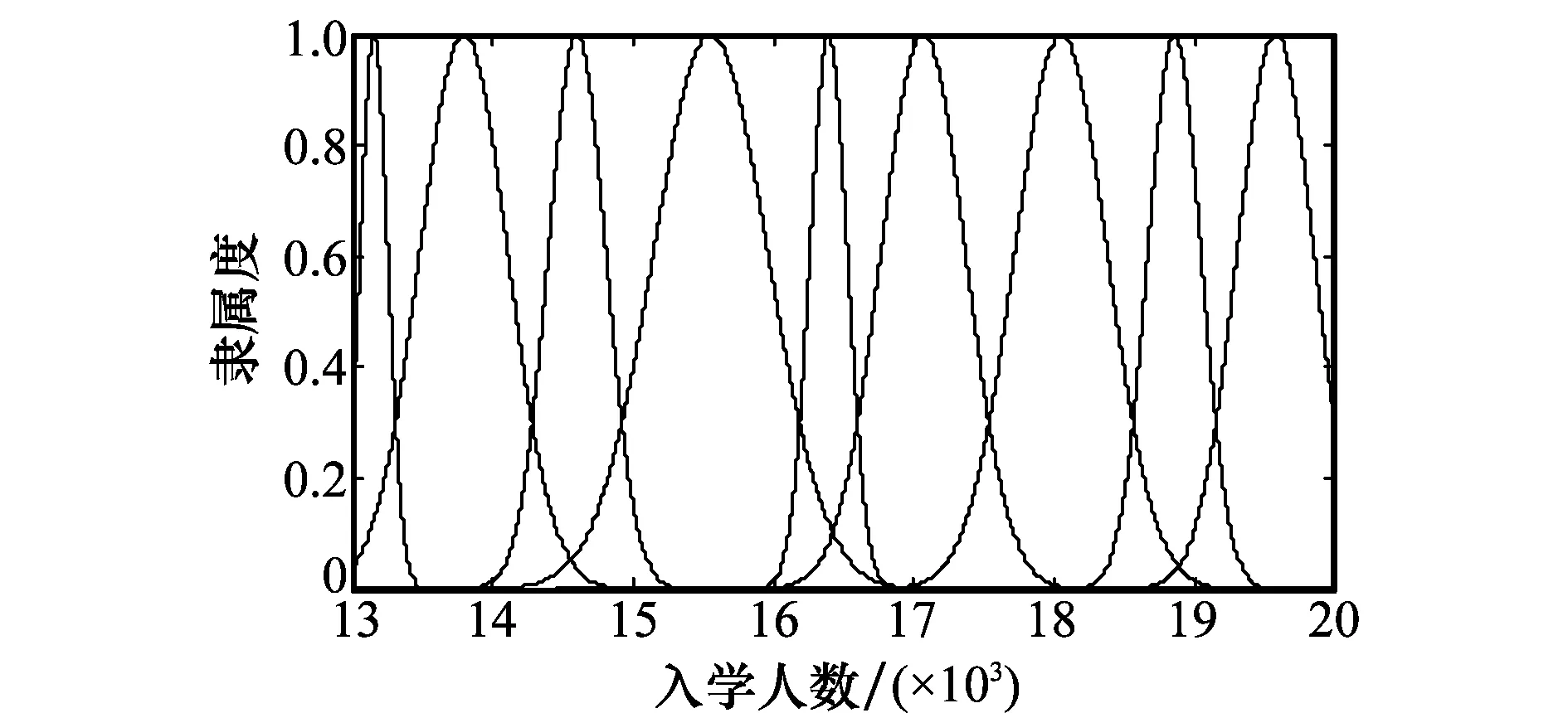
图1 各直觉模糊集的隶属度函数

图2 各直觉模糊集的非隶属度函数
进而得到历史数据对各直觉模糊集的隶属度、非隶属度和直觉指数的值。
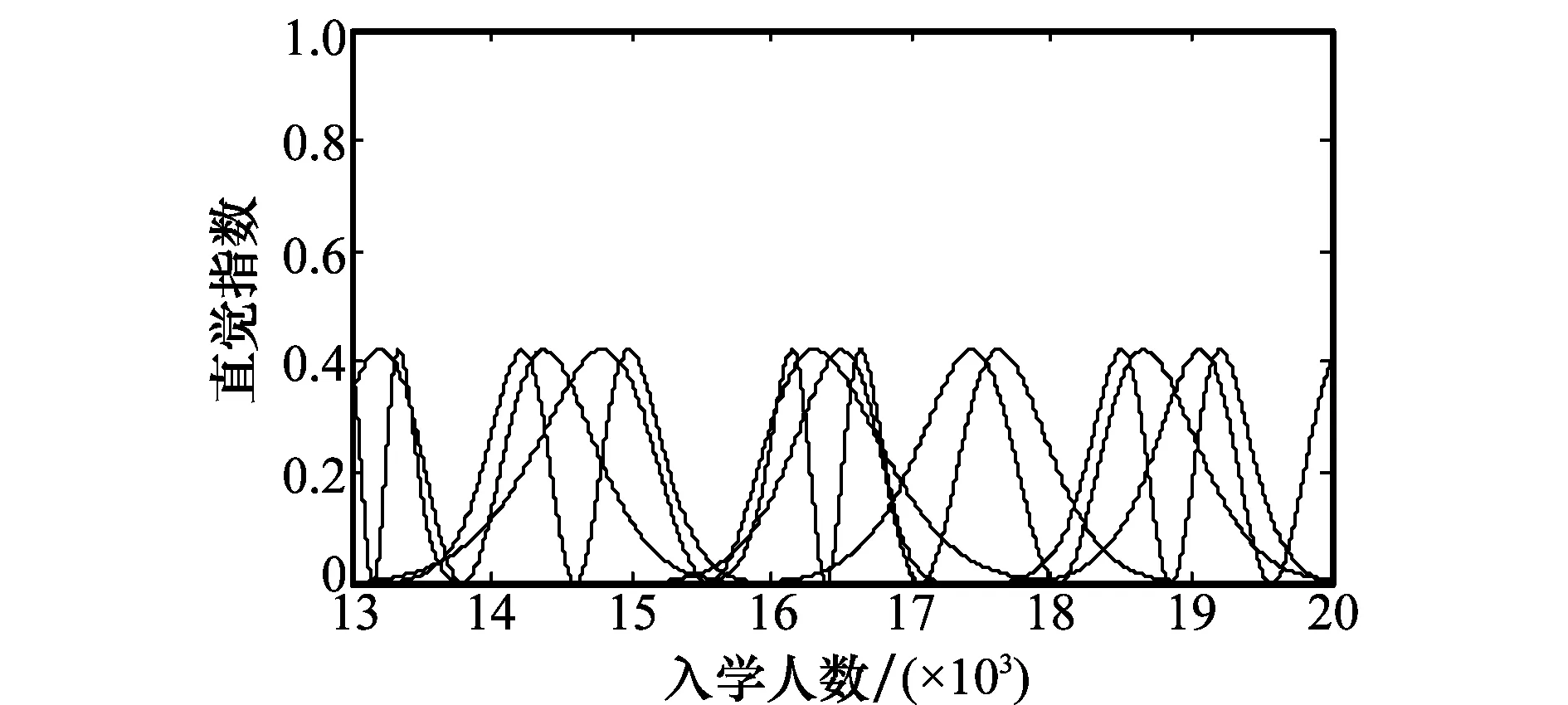
图3 各直觉模糊集的直觉指数函数
步骤 3建立预测规则,求得预测值。
根据第2.3.2节的推理方法,将1971至1991年的21年招生数据分别记为F1,F2,…,F21,建立推理模型

规则:IF x is F1THENy is F2IF x is F2THENy is F3︙IF x is F20THENy is F21输入:IF x is F21输出:y is F*22
计算得
〈0.687,0.207〉/A8+〈0.039,0.616〉/A9

步骤 4预测结果去模糊化输出。
按式(30)的方法计算去模糊化结果为
C0=18.854 5≈18.855
(31)
即1992年招生人数的预测值为18 855。
为检验模型性能,分别采用文献[1]、文献[5]、文献[12]中的模型及本文模型对该数据集进行预测,所得结果如表2所示。其中文献[12]是IFTS预测模型,文献[1]和文献[5]是FTS预测模型,并且在文献[5]中分别给出了将论域划分为7、17、22个区间的预测结果,考虑到历史数据只有22个,将论域划分为17和22个区间的情况并不符合实际应用需求,因此本文只采用其7区间划分的方法。

表2 各模型对Alabama大学入学人数的预测结果

续表2
根据均方误差(root mean square error, RMSE)和平均预测误差(average forecasting error, AFE)两项指标将本文的预测模型同其他3种模型进行比较,指标的计算公式如下,计算结果如表3所示。
(32)

(33)
3.2社会消费品零售总额数据集实验
社会消费品零售总额数据集是由中国国家统计局提供的以月为单位对中国市场的消费品零售总额进行的统计,本文只选取从1991年1月至1994年1月间的37个数据构成实验数据集,其中1994年1月的值120.85作为待预测值,之前36个数据作为历史数据值,如表4所示。
在该数据集上应用文献[1]、文献[5]、文献[12]中的模型及本文模型进行预测,预测值及实际值如图4所示。各模型预测性能如表5所示。

图4 各模型对社会消费品零售总额数据集的预测结果
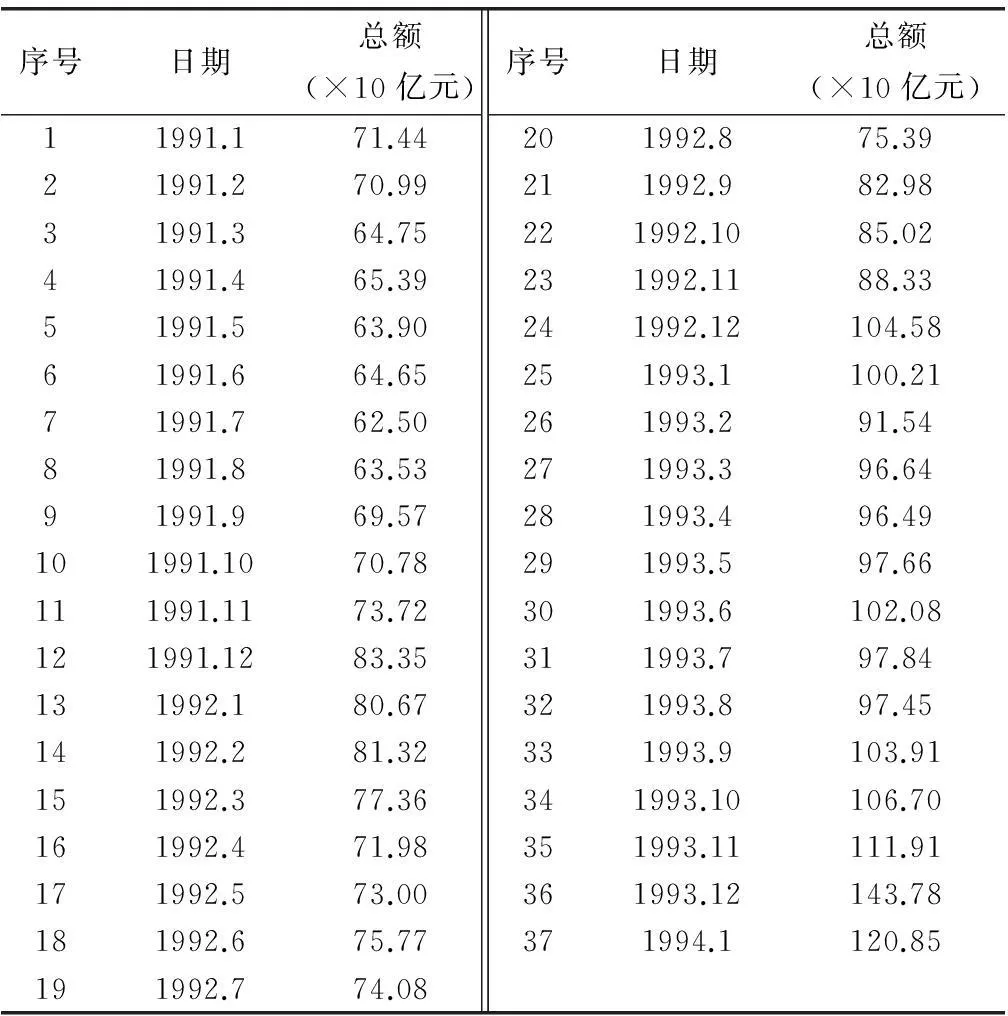
序号日期总额(×10亿元)11991.171.4421991.270.9931991.364.7541991.465.3951991.563.9061991.664.6571991.762.5081991.863.5391991.969.57101991.1070.78111991.1173.72121991.1283.35131992.180.67141992.281.32151992.377.36161992.471.98171992.573.00181992.675.77191992.774.08序号日期总额(×10亿元)201992.875.39211992.982.98221992.1085.02231992.1188.33241992.12104.58251993.1100.21261993.291.54271993.396.64281993.496.49291993.597.66301993.6102.08311993.797.84321993.897.45331993.9103.91341993.10106.70351993.11111.91361993.12143.78371994.1120.85

表5 各模型对社会消费品零售总额数据集的预测性能
4结束语
本文针对模糊时间序列预测方法的不足,利用直觉模糊集在处理不确定数据集上的优势,建立了一个新的直觉模糊时间序列预测模型。采用基于最大支撑树的模糊聚类算法实现论域的非等分划分,使得论域划分这一基础步骤更具实时性和简捷性;针对划分数据的实际特性,给出一种更客观的直觉模糊集隶属度和非隶属的确定方法;采用直觉模糊近似推理建立序列数据的预测规则,更有效的预测不确定数据的模糊变化特征。通过在两类数据集上与经典算法的对比试验表明模型具有较好的预测性能。如何建立多元、高阶直觉模糊时间序列,进一步提高预测性能,将是下一步研究的重点。
参考文献:
[1] Song Q, Chissom B S. Fuzzy time series and its models[J].FuzzySetsandSystems, 1993, 54(3): 269-277.
[2] Song Q, Leland R P, Chissom B S. Fuzzy stochastic fuzzy time series and its models[J].FuzzySetsandSystems, 1997, 88(3): 333-341.
[3] Huarng K. Effective lengths of intervals to improve forecasting in fuzzy time series[J].FuzzySetsandSystems, 2001, 123(3): 387-394.
[4] Lu W, Pedrycz W, Liu X, et al. The modeling of time series based on fuzzy information granules[J].ExpertSystemswithApplications, 2014, 41(8): 3799-3808.
[5] Lu W, Chen X, Pedrycz W, et al. Using interval information granules to improve forecasting in fuzzy time series[J].InternationalJournalofApproximateReasoning, 2015, 57: 1-18.
[6] Chen C H, Chen Y S, Wu Y L. Forecasting innovation diffusion of products using trend weighted fuzzy time-series model[J].ExpertSystemswithApplications, 2009, 36(2):1826-1832.
[7] Egrioglu E, Aladag C H, Yolcu U, et al. Finding an optimal interval length in high order fuzzy time series[J].ExpertSystemswithApplications, 2010, 37(7): 5052-5255.
[8] Aladag C H, Basaran M A, Egrioglu E, et al. Forecasting in high order fuzzy times series by using neural networks to define fuzzy relations[J].ExpertSystemswithApplications, 2009, 36(3): 4228-4231.
[9] Singh P, Borah B. An efficient time series forecasting model based on fuzzy time series[J].EngineeringApplicationsofArtificialIntelligence, 2013, 26(10): 2443-2457.
[10] Chen S M, Chen S W. Fuzzy forecasting based on two-factor second-order fuzzy-trend logical relationship groups and the probabilities of trends of fuzzy logical relationships[J].IEEETrans.onCybernetics, 2015, 45(3): 405-417.
[11] Castillo O, Alanis A, Garcia M, et al. An intuitionistic fuzzy system for time series analysis in plant monitoring and diagnosis[J].AppliedSoftComputing, 2007, 7(4): 1227-1233.
[12] Joshi B P, Kumar S. Intuitionistic fuzzy sets based method for fuzzy time series forecasting[J].CyberneticsandSystems:anInternationalJournal, 2012, 43(1): 34-47.
[13] Zheng K Q, Lei Y J, Wang R, et al. Modeling and application of IFTS[J].ControlandDecision, 2013, 28(10): 1525-1530. (郑寇全, 雷英杰, 王睿, 等. 直觉模糊时间序列建模及应用[J].控制与决策, 2013, 28(10): 1525-1530.)
[14] Zheng K Q, Lei Y J, Wang R, et al. Method of long-term IFTS forecasting based on parameter adaptation[J].SystemsEngineeringandElectronics, 2014, 36(1): 99-104. (郑寇全, 雷英杰, 王睿, 等. 参数自适应的长期IFTS预测算法[J].系统工程与电子技术, 2014, 36(1): 99-104.)
[15] Liang B S, Cao D L.Fuzzymathematicsandapplications[M]. Beijing: Science Press, 2007, 75-77.(梁保松,曹殿立.模糊数学及其应用[M].北京:科学出版社,2007,75-77.)
[16] Lei Y. Research on target recognition techniques based on intuitionistic fuzzy sets and kernel matching pursuit[D]. Xi’an: Air Force Engineering University, 2012. (雷阳. 基于直觉模糊核匹配追踪的目标识别方法研究[D]. 西安: 空军工程大学,2012.)
[17] Lei Y J, Zhao J, Lu Y L, et al.Theoriesandapplicationsofintuitionisticfuzzyset[M]. Beijing: Science Press, 2014: 145-155. (雷英杰, 赵杰, 路艳丽, 等. 直觉模糊集理论及应用[M]. 北京: 科学出版社, 2014: 145-155.)
王亚男(1988-),女,博士研究生,主要研究方向为网络信息安全。
E-mail:wyn1988814@163.com
雷英杰(1956-),男,教授,博士研究生导师,主要研究方向为人工智能、网络信息安全。
E-mail:leiyjie@163.com
王毅(1979-),男,讲师,博士后,主要研究方向为智能信息处理。
E-mail:wangyi.kgd@gmail.com
范晓诗(1988-),男,博士研究生,主要研究方向为网络信息安全。
E-mail:fan_xs@126.com
Intuitionistic fuzzy time series model based on intuitionistic fuzzy reasoning
WANG Ya-nan, LEI Ying-jie, WANG Yi, FAN Xiao-shi
(AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi’an710051,China)
Abstract:The objectivity of the fuzzy time series (FTS) forecasting theory in description of uncertain data sets is limited by the fuzzy sets theory. To break this limitation, an intuitionistic FTS (IFTS) forecasting model is built. Firstly, the fuzzy clustering algorithm is used to get unequal domain-dividing intervals. And then a more objective construction method of membership and non-membership functions of intuitionistic fuzzy sets (IFS) is proposed. Thirdly, forecasting rules based on intuitionistic fuzzy approximate reasoning are given. Finally, experiments on datasets of enrollments of the university of Alabama and the total retail sales of social consumer goods of China are carried out which show that the new model improves the prediction accuracy with its validity and superiority.
Keywords:intuitionistic fuzzy time series (IFTS); fuzzy cluster; membership; non-membership; intuitionistic fuzzy reasoning
收稿日期:2015-06-04;修回日期:2015-09-02;网络优先出版日期:2015-12-23。
基金项目:国家自然科学基金(61402517);陕西省自然科学基金(2013JQ8035)资助课题
中图分类号:TP 393.08
文献标志码:A
DOI:10.3969/j.issn.1001-506X.2016.06.18
作者简介:
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20151223.1030.016.html

