颗粒阻尼复合板结构振动响应预估
苏俊收,耿彦波,高磊磊
(江苏徐州工程机械研究院,江苏,徐州,221004)
颗粒阻尼复合板结构振动响应预估
苏俊收,耿彦波,高磊磊
(江苏徐州工程机械研究院,江苏,徐州,221004)
本文运用等效粘性阻尼模型,结合有限元软件,对颗粒阻尼复合板的稳态振动响应进行了预估,并进行了相应的实验验证,得到的理论预估结果与实验结果具有较好的一致性,说明等效黏性阻尼模型可以推广应用到颗粒阻尼复合板结构振动响应预估中;之后,通过实验分析了颗粒阻尼器不同布局、不同质量、不同颗粒对减振效果的影响,发现颗粒阻尼器阻尼特性表现出很大的差异,不仅各阶振型表现不同,不同测量点也是差异很大,但总体上表现出了良好的宽频减振特性,本文的研究为颗粒阻尼复合板结构的推广应用奠定了基础.
颗粒阻尼复合板; 等效黏性阻尼; 振动响应
颗粒阻尼技术具有减振频带宽、附加重量轻、适合于恶劣环境下工作等其他阻尼技术无可比拟的优点[1].工程车辆由于在野外作业,作业条件恶劣,自重吨位大、负荷变化频繁的特点,自身振动较大.颗粒阻尼技术虽然在航空、汽车等领域已有了初步的发展[2][3][4],但在工程机械领域的研究却很鲜见.随着工程车辆作业条件更加复杂,减振要求更加迫切,轻量化趋势日益推进,颗粒阻尼技术的优点变得更加突出,在工程机械行业中的应用前景更加巨大.
颗粒阻尼复合板结构是通过在结构体的内部加工适当大小和适当数量的孔洞或者在其上面安装附属装置,并将颗粒体装入其中的孔洞或附属装置内使之处于非阻塞的状态.这样当结构体振动时就会带动其中的颗粒体振动,颗粒体与颗粒体相互之间以及颗粒与结构体之间的不断碰撞、摩擦就会消耗掉结构体的振动,从而起到减振的作用.颗粒阻尼几乎不受温度限制,布置位置非常灵活,可以附加于工程车辆结构构件的外部,也可以内嵌于结构构件中,且在任意夹层、内部空洞均可置放,不影响结构使用,也不会增加较大重量.
由于颗粒阻尼减振机理较为复杂,目前仍没有很好的理论来指导其应用,这在一定程度上影响了颗粒阻尼技术进一步的应用,西安交通大学的吴成军教授开发出一种基于气固两相流理论的颗粒阻尼减振效果预估模型,并应用该模型进行颗粒阻尼悬臂梁的强迫振动响应预估与分析中,本文运用吴教授提出的等效黏性阻尼模型,对更为复杂的颗粒阻尼复合板结构进行研究,推进颗粒阻尼技术的进一步应用.
1 理论预估
本部分仿真用的板如图1所示,板采用的材料为铝合金,其密度为2 700 kg/m3,弹性模量为56 GPa;板的厚度为6 mm,夹持区域为60 mm×50 mm的长方体,悬空区域为300 mm×200 mm的长方体.颗粒阻尼器的腔体为直径14 mm,高20 mm的圆柱体,其质量为11.45 g,填充颗粒为钨粒,密度为17 000 kg/m3,平均粒径为0.3 mm.阻尼器、激励点以及测量点的位置如图1所示.

图1 颗粒阻尼板仿真示意图Fig.1 Simulation diagram of particle-damping plate
仿真应用多物理场耦合软件ANSYS以及MATLAB软件进行计算.仿真前,先根据实际条件建立模型.通过实验测量光板的加速度响应,应用半功率带宽法求得结构的阻尼损耗因子为0.018.仿真时,根据实际条件施加相应的约束以及激励.阻尼器的影响通过一个集中质量及集中力来模拟.集中质量等于阻尼器的质量,而集中力为一个随着阻尼器施加点速度变化的量,其表达式集中力表达式为[5]:
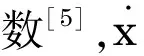

式中m——系统的质量矩阵;
k——系统的刚度矩阵;
c——系统固有阻尼矩阵;
f——阻尼器的等效力矢量;
F——系统所施加的外力矢量.
由于该部分仿真进行的是谐响应分析,而上述集中力是一个随着施加点速度变化的力,在ANSYS中进行谐响应分析时是不能直接施加这样一个随着时间变化的力的.通过分析,发现可以通过弹簧系统来施加该力,可以将弹簧的粘性力设为上述力表达式.这样,我们就巧妙地实现了颗粒阻尼在板上的模拟.
仿真时夹持区域采用固定约束,在如图1所示的三个位置施加颗粒阻尼器,阻尼器的质量填充比均设定为40%.计算在正弦激励力的作用下,如图所示的12个测量点的加速度响应.为对比方便,计算出各个测量点的加速度传递函数(加速度与激励力的比值),图2列出了未施加阻尼器以及施加阻尼器时板的其中几个测量点的加速度传递函数.

图2 颗粒阻尼板的加速度传递函数Fig.2 Acceleration transfer function of particle-damping plate
从图2中的仿真结果可以看出,施加颗粒阻尼器之后,板的加速度传递函数幅值有着较为明显的降低,对于几个测量点的各阶峰值都有一定程度的降低,而第四阶峰值的降低尤为明显.
2 实验验证
为验证理论预估结果的正确性,进行相应的实验验证,实验装置图如图3所示,实验中的各参数与理论预估中相同.由于需要计算加速度响应的传递函数,本文同时测试测量点的加速度信号以及激励点的激励力信号.将测量到的数据与仿真结果放在一起对比,光板(未施加阻尼器)的加速度传递函数仿真结果及实验结果对比如图4所示,施加颗粒阻尼器的板的加速度传递函数仿真结果及实验结果对比如图5所示.

图3 颗粒阻尼板实验装置图Fig.3 Experimental apparatus diagram of particle-damping plate

图4 光板(未施加阻尼器)的加速度传递函数Fig.4 Acceleration transfer function of plate without damper
图4中,本文列出了光板部分测量点的加速度传递函数的仿真结果与实验结果对比.从中可以看出,光板的仿真结果与实验结果有着较好的吻合度,在第二阶振型峰值处两者基本完全重合,但在第四阶固有频率处误差较大.通过该结果对比,我们可以证明光板的仿真结果是正确的,可以以此参数设置进行颗粒阻尼板的仿真.

图5 颗粒阻尼板的加速度传递函数结果对比Fig.5 Comparison of acceleration transfer function of plate without damper
在图5中,列出了在板上施加质量填充比为40%的颗粒阻尼器时,板的部分测量点的加速度传递函数仿真结果与实验结果对比.从图中可以看出,仿真结果与实验结果一致性较好,在很多区域内基本重合.这证明本文仿真是非常成功的,同时也说明本文对于颗粒阻尼的模拟是正确的.对于颗粒阻尼板,我们可以较好地预估其振动响应.
3 参数影响
3.1 不同阻尼器布局对减振效果的影响
通过实验研究了颗粒阻尼器的施加位置组合对板的减振效果的影响,同样使用三个阻尼器(固定质量填充比为40%),选取12个测点.阻尼器的布局变化如图6所示(布局一的示意图如图1),同时测出测量点的加速度响应以及激励点的激励力,列出几个测量点的加速度传递函数如图7所示.
从图 7可以看出,颗粒阻尼器的布局形式会严重影响其减振效果.总体而言,基本上是在二阶共振峰值处,布局四减振效果最好;在三阶共振峰值处,布局三减振效果最好;在四阶共振峰值处,布局五减振效果最好.这样的结果主要是由于阻尼器的布局位置刚好接近该阶模态振型的峰值位置而导致的.这就告诉我们,若需要主要降低某阶频率的峰值时,在其振型峰值处布置阻尼器,可以达到较好的效果.另外,我们还可以发现,减振效果越好,其共振峰位置偏离光板固有频率就越严重.这是由于当取得较好的减振效果时,阻尼器的振动幅度相对较小,颗粒基本停在阻尼器上,因此,颗粒对系统固有频率影响就越小,偏离光板固有频率就越大.

图6 阻尼器布局图Fig.6 Layout diagram of damper

图7 颗粒阻尼板的加速度传递函数(阻尼器布局影响)Fig.7 Acceleration transfer function of particle-damping plate(damper layout influence)
3.2 阻尼器、质量块减振效果对比
通过实验研究了颗粒阻尼器以及质量块对板的振动的影响,同样选用三个阻尼器(填充颗粒为钨粉),同时选取三个质量块进行试验.三个质量块的质量分别为:26.37 g(1号),25.47 g(2号),24.59 g(3号),填充颗粒使得三个阻尼器的质量与三个质量块一致,阻尼器(或质量块)以及测量点的布置如图1所示,其中3号阻尼器(或质量块)位于中间处,列出几个测量点的加速度传递函数如图8所示.
从上述测量结果可以看出,除个别测量点的某些频率处(测点10的1 100 Hz左右),外,颗粒阻尼器都取得了较好的减振效果,基本上在每个峰值频率处减振效果都较好.这说明颗粒阻尼器减振的宽频特性.而只加质量块则基本没有降低峰值(在某些频率处降低,而在某些频率处升高);另外,还可以看出,虽然阻尼器的质量和质量块相同,但施加阻尼器的板的各阶固有频率比添加质量块的较高一点.
3.3 不同类型颗粒对减振效果的影响
通过实验研究了颗粒材料对于颗粒阻尼器的减振效果的影响.这里,同样使用三个阻尼器(固定质量填充比为40%),选取12个测点,阻尼器以及测量点的布置如图1所示.分别选取0.3 mm的白刚玉、铁粉和钨粉进行实验.三种材料如图9所示,列出几个测量点的加速度传递函数如图10所示.

图8 颗粒阻尼板的加速度传递函数(减振效果)Fig.8 Acceleration transfer function of particle-damping plate(vibration damping influence)

图9 颗粒阻尼材料Fig.9 Particle-damping material
图10中列出的为3号、4号和8号测量点的加速度传递函数响应.从图中可以很明显的看出,钨粉的减振效果最好,铁粉次之,而白刚玉最差.这是因为在材料密度方面,也是钨粉最大,铁粉次之,而白刚玉最小.因此,固定填充比时,钨粉填充质量最大,所以取得最好的减振效果.另外,在不同测点体现出的效果也不同,如钨粉在测点8的第四阶峰值处减振效果非常好,而在测点3的第四阶峰值处的减振效果比另外两者还差.
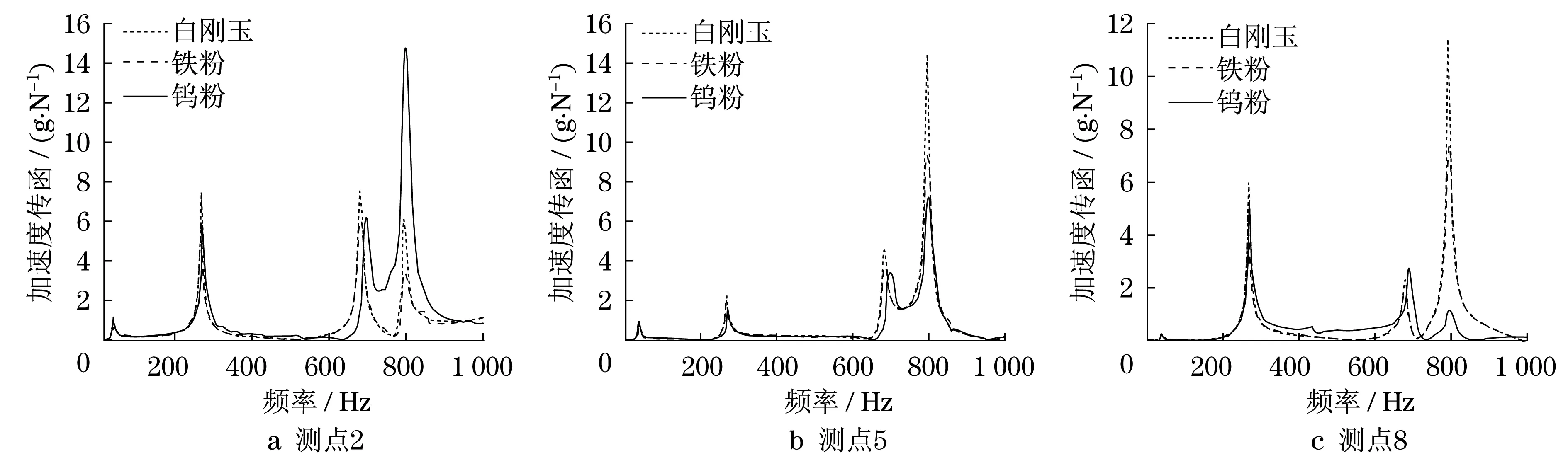
图10 颗粒阻尼板的加速度传递函数(颗粒材料影响)Fig.10 Acceleration transfer function of particle-damping plate(particle-damping material influence)
4 结论
本文以气固两相流理论的颗粒阻尼减振效果预估模型为基础,结合多物理场耦合软件ANSYS对颗粒阻尼复合板的稳态振动响应进行了预估.得到的理论预估结果与实验结果一致性较好,说明本文所运用的模型对颗粒阻尼复合板的振动响应的预估是成功的,这为颗粒阻尼复合板的进一步扩展应用奠定了基础.本文在颗粒阻尼复合板的理论预估及实验的过程中,发现颗粒阻尼器对板的减振效果表现出很大的差异性,不仅各阶振型表现不同,不同测量点也是差异很大,但总体上表现出了良好的宽频减振特性.
[1] 吴成军.工程振动与控制[M].西安:西安交通大学出版社,2008.
WU Chengjun.Engineering vibration and control[M].Xi′an:Xi′an Jiao Tong University Publishers,2008.
[2] 申智春.颗粒阻尼在航天器减振中的应用与前景[J].应用力学学报,2011,28(6):608-612.
SHEN Zhichun.Application of particle damping in spacecraft vibration suppression[J].Chinese Journal of Applied Mechanics,2011,28(6):608-612.
[3] 夏兆旺,魏守贝.颗粒阻尼技术在制动鼓减振方面的应用研究[J].振动工程学报,2010,27(6):893-899.
XIA Zhaowang,WEI Shoubei,WEN Huabing.Application of particle damping in vibration attenuation of brake drum[J].Journal of Vibration Engineering,2010,27(6):893-899.
[4] 吴成军,杨瑞超,王东强.基于气体-颗粒两相流理论的颗粒阻尼悬臂梁振动响应预估[J].机械工程学报,2013,49(10):53-61.
WU Chengjun,YANG Ruichao,WANG Dongqiang.Prediction on vibration response of cantilever particle-damping beam based on two-phase flow theory of gas-particle[J].Journal of Mechanical Engineering,2013,49(10):53-61.
[5] 闫维明,黄韵文.颗粒阻尼技术及其在土木工程中的应用展望[J].世界地震工程,2010,26(4):18-24.
YAN Weiming,HUANG Yunwen,HE Haoxiang.Particle damping technology and its application prospect in civil engineering[J].World Earthquake Engineering,2010,26(4):18-24.
[6] 倪振华.振动力学[M].西安:西安交通大学出版社.2005.
NI Zhenhua.Vibration mechanics[M].Xi′an:Xi′an Jiao Tong University Publishers,2005.
Pre-assessment on vibration responses from multiplex particle-damping plates
SU Jun-shou,GENG Yan-bo,GAO Lei-lei
(Jiangsu Xuzhou Construction Machinery Research Institute XCMG,Xuzhou 221004,China)
Based on previous works, an improved analytical model for equivalent viscous damping is first proposed. Then, the forced responses from a particle-damping plate is pre-assessed using the improved model and finite element method. Accordingly, the theoretical results are coincided with experimental ones. Finally, it is found that this model can rapidly and efficiently estimate vibration responses from particle-damping plates. Furthermore, the combination of three dampers in terms of different positions, masses and filling ratios is analyzed via testing with different damping properties, such as vibration modes and responses from measuring points. Nevertheless, good broadband vibration characteristics are generally detected. Therein, this approach is significant on practicality for particle-damping plates.
multiplex particle-damping plate; equivalent viscous damping; vibration response
苏俊收(1988-),男,硕士,工程师.E-mail:sujunshou@163.com
U 463.1
A
1672-5581(2016)06-0493-06

