水下三维无线传感器网络节点部署研究*

黄　珏　颜　冰

(海军工程大学兵器工程系　武汉　430033)



水下三维无线传感器网络节点部署研究*

黄珏颜冰

(海军工程大学兵器工程系武汉430033)

摘要在地面无线传感器网络中，一般是假设所有的传感器节点都处于同一个二维平面上，而对于水下传感器网络来说，由于传感器节点可以部署在不同的海深，因此也就构建了一个三维网络。论文针对水下三维传感器网络的部署问题进行研究，分析了常用的空间填充多面体在空间部署中的特性，给出了各种空间填充多面体在空间中的部署模式，进一步提出了在保持完全覆盖和连通的前提下各个节点部署坐标之间的相互关系，并对截顶正八面体的部署方式进行了仿真。为三维无线传感器网络节点部署提供了方法。

关键词三维无线传感器网络; 节点部署; 空间填充多面体; 覆盖性; 连通性

Class NumberTP291.1

1引言

本文针对三维网络空间中传感器节点位置部署问题进行研究，对空间填充多面体进行了分析，推导计算了在rc/rs为任何比值下应用各空间填充多面体时节点部署坐标的相互关系，最后对截顶正八面体的部署节点坐标进行了仿真。

2问题描述

为了更好地研究传感器节点对特定空间的全覆盖问题，作如下的假设:

1) 传感器的测量范围为以自身位置为球心，以探测范围rs为半径的球形区域。

2) 传感器的通信范围为空间内任何与传感器的距离小于rc的节点。

3) 网络中所有的传感器都具有相同的测量和通信范围。

4) 相比于要覆盖的三维空间网络，传感器的测量和通信范围非常小，边界效应可以忽略不计。

假设传感器网络节点可以根据拓扑控制算法的需要部署在空间的任意位置，为了满足空间的完全覆盖性，所有的节点都能与自身的所有相邻节点保持连通性，本文所要研究的问题即为如何使用最少的传感器节点对三维空间进行覆盖，同时部署传感器节点的坐标计算问题。

3问题分析

在前面的问题描述中，假设传感器节点的通信和测量模型都是球形的，但是，由于球形不具备空间填充的性质，定义一种空间填充多面体，这种多面体能够以没有空缺没有重叠的方式紧密地填充一个三维空间。那么就可以用空间填充多面体来对网络中的虚拟单元进行建模，保证虚拟单元中心到该单元最远处的距离不超过网络节点的测量范围，并且相邻两个虚拟单元中心之间的距离不超过节点的通信距离。

定义(Voronoi分割):假设三维欧几里得空间中存在一个离散发生点集S={c1,c2,…,cn}，对于S中的某一发生点ci(ci∈S′)来说，在欧几里得空间中，所有满足到发生点ci的距离小于到S中其他发生点距离的所有点组成的集合，构成了一个凸多面体的内部空间，我们把这个凸多面体成为发生点ci的Voronoi单元。S中所有发生点的Voronoi单元可以用来对整个三维空间进行分割，称为关于发生点集S的Voronoi分割。

立方体、正六棱柱、菱形十二面体和截顶正八面体为独立填充三维空间的多面体，将传感器部署在填充多面体的中心，那么填充多面体构成对三维空间的Voronoi分割，从而对三维空间进行了完全覆盖。

4节点部署坐标计算

对各种常见的空间填充多面体进行分析，推导出各种部署模式下传感器部署的位置坐标。

4.1立方体

立方体是非常简单、非常直观的一种部署模式，在三维空间中，每个传感器节点的部署位置在立方体的中心，节点监测范围所形成的Voronoi单元为其所在的立方体。

(1)

(x,y,z)=

(2)

其中，u，v，w为整数。

4.2正六棱柱

传感器节点部署在正六棱柱的中心，所形成的Voronoi单元为正六棱柱，那么传感器节点的部署位置为正三棱柱的顶点，传感器部署情况如图1所示。

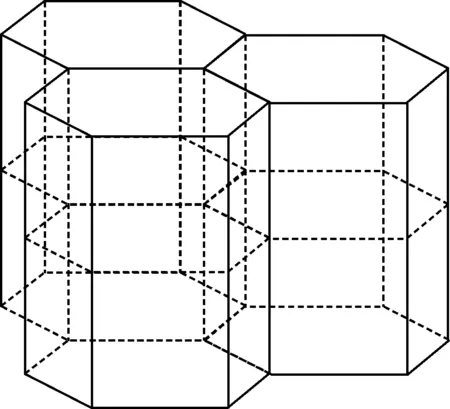
图1　正六棱柱部署情况

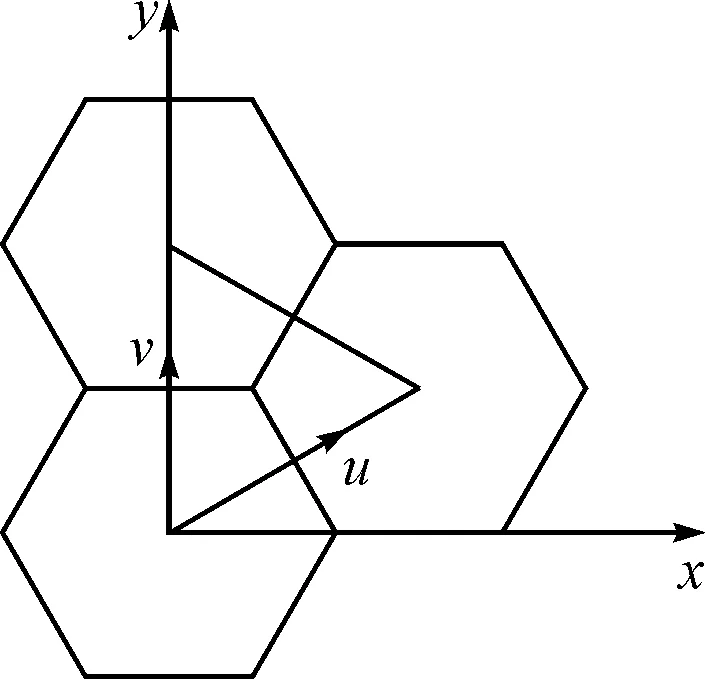
图2　正六棱柱在xy平面上投影

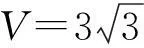
(3)

(4)

(5)

------------------------------其中，u，v，w为整数。

4.3菱形十二面体

菱形十二面体具有全等的十二个菱形面，取两个完全相同的立方体，其中一个沿四条对角线切割，形成了六个正四棱锥，将这六个四棱锥分别叠放在另一个立方体的六个面上，这样就形成了一个菱形十二面体。将传感器节点部署在菱形十二面体的中心，节点的Voronoi单元即为其所在的菱形十二面体。部署情况如图3所示。

假设菱形十二面体的中心到其顶点的距离为R，以中心为原点建立空间直角坐标系xyz，菱形十二面体在xy平面上的投影如图4所示。

图3　 菱形十二面体部署情况

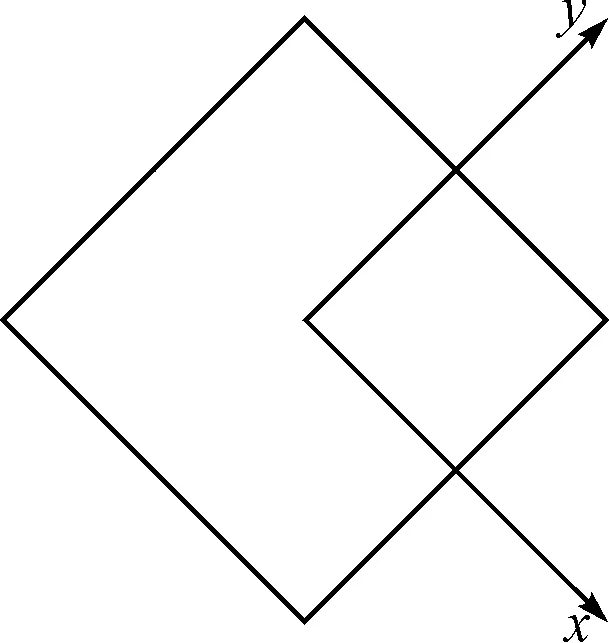
图4　菱形十二面体在xy平面上的投影

菱形十二面体在xz平面上的投影如图5所示。

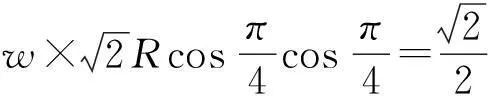
图5　菱形十二面体在xz平面上的投影

(x,y,z)=

(6)

其中，u，v，w为整数。

4.4截顶正八面体

截顶正八面体是将正八面体的每个顶点在边长的1/3处、沿垂直于顶点与中心连线的方向切割，形成了由六个正方形和八个正六边形围成的空间立体图形。将传感器节点部署在中心，传感器节点所形成的Voronoi单元为其所在的截顶正八面体，部署情况如图6所示。

假设中心到截顶正八面体的顶点的距离为R，以中心为坐标原点建立空间直角坐标系xyz，图形在xy平面内的投影如图7所示。

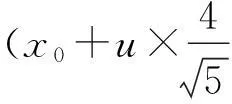
图7　截顶正八面体xy平面内投影

图6　截顶正八面体部署情况

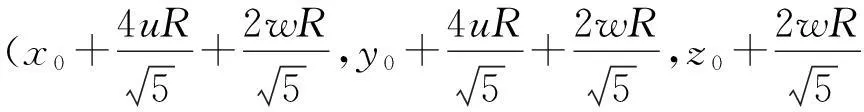
(7)

其中，u，v，w为整数。

5基于截顶正八面体的节点部署坐标实例

图8　节点部署示例

这种部署方式完成了对一个平行六面体的完全覆盖，并且保持了各节点之间的连通性。

6结语

本文根据常用的规则填充多面体的节点部署模式，在充分考虑传感器节点的探测范围和连通范围的基础上，分析计算了各种部署模式在填充时各个节点的部署坐标，最后对截顶正八面体的部署模式进行了仿真，为水下三维传感器节点的部署提供了方法。

参 考 文 献

[1] Watfa M,Commuri S.A coverage algorithm in 3D wireless sensor network[C]//The 1stInt Symposium on Wireless Pervasive Computing.Phuket:IEEE Press,2006:10-16.

[2] Akkaya K,Newell A.Self-deployment of sensors for maximize coverage in underwater sensor network[J].Elsevier J of Computer Communications,2009,32(7):1233-1244.

[3] Alam S N,Haas Z J,Coverage and connectivity in three-dimensional underwater sensor networks[C]//Proc of ACM MobiCom.Los Angeles:ACM Press,2006:346-357.

[4] Dario Pompili, Tommaso Melodia, Lan F.Akyildiz.Deployment Analysis in Underwater Acoustic Wireless Sensor Networks[C]//WUWNet’06,September 25,2006:48-55.

[5] S.M.Nazrul Alam, Zygmunt J. Haas. Topology Control and Network Lifetime in Three-Dimensional Wireless Sensor Network[J/OL]. http://wnl.ece.cornell.edu.

[6] Wendi B.Heinzelman, Anantha P.Chandrakasan, Hari Balakrishnan. An Application-Specific Protocol Architecture for Wireless Microsensor Netwok[C]//IEEE Transactoins on Wireless Communications,2002(4):660-670.

[7] 温俊，窦强，蒋杰，等.无线传感器网络中保证覆盖的最少节点部署[J].国防科技大学学报，2009,31(3):76-81.

[8] 钟永信，黄建国，韩晶. 三维无限传感器网络部署、覆盖和连接问题研究[J].控制与决策，2011,26(10):1447-1451.

[9] 张云洲，吴成东，程龙，等.确定性空间的无线传感器网络节点部署策略研究[J].控制与决策，20105(11):1625-1629.

[10] 何欣，桂小林，安健.面向目标覆盖的无线传感器网络确定性部署方法[J].西安交通大学学报，2010，44(6):6-15.

[11] 刘丽萍，王智，孙优贤.无线传感器网络部署及其覆盖问题研究[J].电子与信息学报，2006,28(9):1752-1757.

Node Deployment in Three Dimensional Under-water Wireless Sensor Networks

HUANG JueYAN Bing

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan430033)

AbstractFor the on land wireless sensor network, it is often considered that all the sensors are in one plane. But for the under-water wireless sensor network, the sensors can be deployed at different depths. So the three dimensional sensor networks are built. To solve the problem of the node deployment in three dimensional under-water wireless sensor networks, the character in the space deployment of the space-filling polyhedron is analyzed. And the deployment modes of each space-filling polyhedron are provided. This method can calculate the relationship of the coordinate of each node in promise of both coverage and connectivity. In the end, the deployment of the truncated octahedron is chosen to be simulated. This method provides an effective way to solve the problem of the node deployment in three dimensional under-water wireless sensor networks.

Key Wordsthree dimensional wireless sensor networks, node deployment, space-filling polyhedron, coverage, connectivity

* 收稿日期：2015年11月24日,修回日期：2015年12月30日

作者简介：黄珏，男，博士研究生，研究方向：军用目标识别及信息感知技术。颜冰，女，博士，教授，研究方向：军用目标识别及信息感知技术。

中图分类号TP291.1

DOI：10.3969/j.issn.1672-9730.2016.05.039