基于卡尔曼滤波的动态定位优化*

陈　刚　王　威　狄　鹏

(1.海军工程大学管理工程系　武汉　430033)(2.海军工程大学舰船工程系　武汉　430033)



基于卡尔曼滤波的动态定位优化*

陈刚1王威2狄鹏1

(1.海军工程大学管理工程系武汉430033)(2.海军工程大学舰船工程系武汉430033)

摘要针对动态定位中存在很多随机因素影响定位精度的问题，本文将卡尔曼滤波技术应用于动态定位中，设计出了卡尔曼滤波器，对随机因素造成的误差进行滤波以减小定位误差，提高了定位精度。卡尔曼滤波技术是一种线性最小方差滤波估计，它只需要通过上一时刻状态向量的最优估计和现在时刻的观测量就可以得到现在时刻状态向量的最优估计值。论文首先以物体在二维空间运动为例，建立系统的状态转移方程以及测量方程，然后采用滤波器对测量值进行滤波处理，最后采用算例进行仿真。仿真结果表明,将卡尔曼滤波技术应用于动态定位中，能有效地优化动态定位，提高定位精度。

关键词卡尔曼滤波; 动态定位; 随机因素; 状态; 最优估计

Class NumberP228

1引言

如何获得准确的位置和时间信息对于目前的社会活动极其重要，在实际动态定位中，会存在很多随机干扰因素影响定位的精度，例如使用GPS定位时，卫星的星历误差、卫星钟差、多路径效应、接收机本身的噪声、电离层及对流层等都会对定位产生干扰。随着时代发展，定位技术也不断成熟，传输时延差TDOA[1～4]、差分GPS[5～7]等定位技术使定位精度不断提高，但因需要建立差分GPS基准站以及受到差分GPS所面临的信号作用范围限制，在很多特殊场合满足不了定位精度要求，迫切需要新的技术来提高定位精度。卡尔曼博士在1961年提出了一种线性滤波估计理论，即卡尔曼滤波[9～10]，这种滤波引入了控制理论状态空间的概念，只需要通过上一时刻状态向量的最优估计和现在时刻的观测量，然后在时域内进行线性递推计算，就可将真实的状态从各种干扰中实时最优地估计出来。卡尔曼滤波已成功应用于动态数据处理[11]、惯性导航[12～14]中，使用卡尔曼滤波和其它算法相结合能有效地减少动态定位中的误差，提高定位的精度。

2卡尔曼滤波算法

卡尔曼滤波算法是一种递推的线性最小方差估计方法，它通过建立状态方程和量测方程来描述系统的动态变化过程。由前一时刻的估计值和新获得的观测数据，依据滤波增益矩阵的变化，递推计算出新的估计值，最后得到系统状态的最优估计。无需存储不同时刻的观测数据，便于实时数据处理。因此被广泛应用于船舶、雷达以及导航等动态定位的数据处理中。

假设系统的状态向量为X，观测向量为Z，观测向量Z可由状态向量X进行表示，观测方程为

Z(k)=H(k)X(k)+V(k)

其中H(k)表示观测矩阵，V(k)表示观测的噪声。

不考虑控制项，系统由k-1时刻状态转移k时刻状态可由状态转移方程进行表示:

X(k)=Φ(k|k-1)X(k)+W(k)

其中Φ(k|k-1)表示状态转移矩阵，W(k)表示系统过程的噪声。

关于系统过程噪声和观测噪声的统计特性，假定如下:

其中Qk是系统过程噪声W(k)的非负定方差矩阵；Rk是系统观测噪声V(k)的正定方差矩阵，δkj是Kronecker-δ函数。

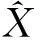
状态一步预测

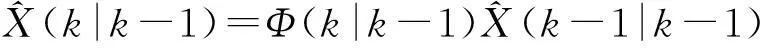
状态估计

^X(k|k) =^X(k|k-1)+K(k)

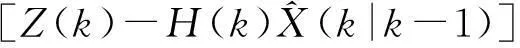
滤波增益矩阵

K(k)=P(k|k-1)H(k)T/H(k)P(k|k-1)H(k)T

一步预测误差方差矩阵

P(k|k-1)=Φ(k|k-1)P(k-1|k-1)

Φ(k|k-1)T+Q(k)

估计误差方差矩阵

P(k|k)=[1-K(k)H(k)]P(k|k-1)

上述方程即为线性离散系统卡尔曼滤波方程。

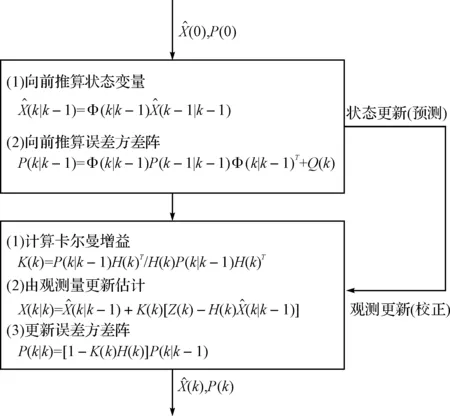
图1　随机线性离散系统卡尔曼滤波器流程图

3卡尔曼滤波器模型的构建

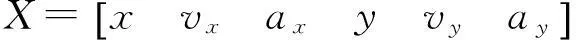
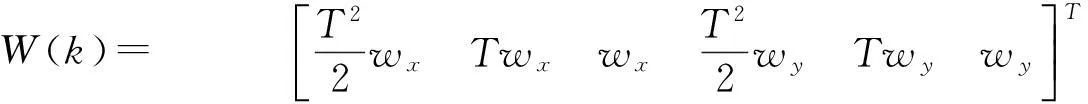
W(k)= T22wxTwxwxT22wyTwywyéëêêùûúúT

,

Z(k)=H(k)X(k)+V(k)

其中

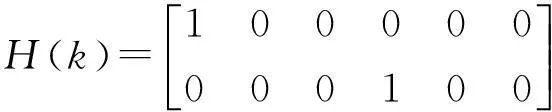
对于系统的过程噪声wx、wy以及系统的测量噪声v1、v2均为不相关的白噪声过程， 其特性如下:

令系统过程噪声方差矩阵为Q(k),系统测量噪声方差矩阵为R(k)，可表示为

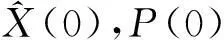
4仿真实验

为了验证所设计的卡尔曼滤波模型的可行性和有效性,进行仿真试验。假设某物体沿x轴方向以速度vx0=5m/s的速度做匀速运动，沿y轴做初速度vy0=5m/s，ay=1m/s2的匀加速运动，采样周期T=0.1s，采样时间为10s。通过仿真模拟出测量噪声为R(k)的观测值Z(k)。设置相关仿真参数。

系统初始化位置及协方差矩阵为

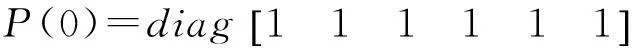
系统过程方差矩阵及测量方差矩阵

采用卡尔曼滤波器对系统观测值Z(k)进行滤波处理，滤波前后结果如图2。

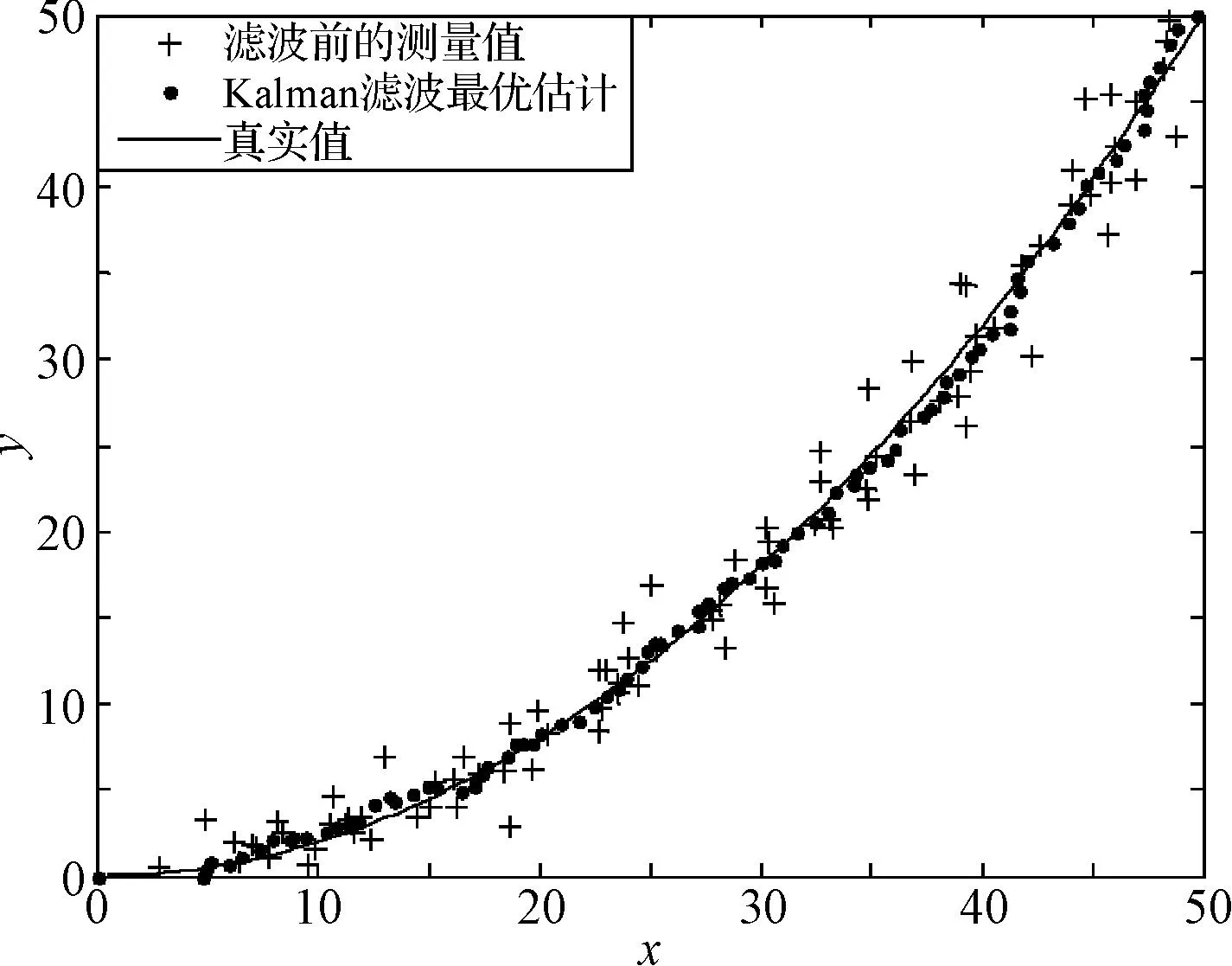
图2　卡尔曼滤波结果

将最优估计值、测量值与真实值进行对比:

=370.04

=40.08

对滤波前后x轴，y轴方向做误差分析如图3和图4。

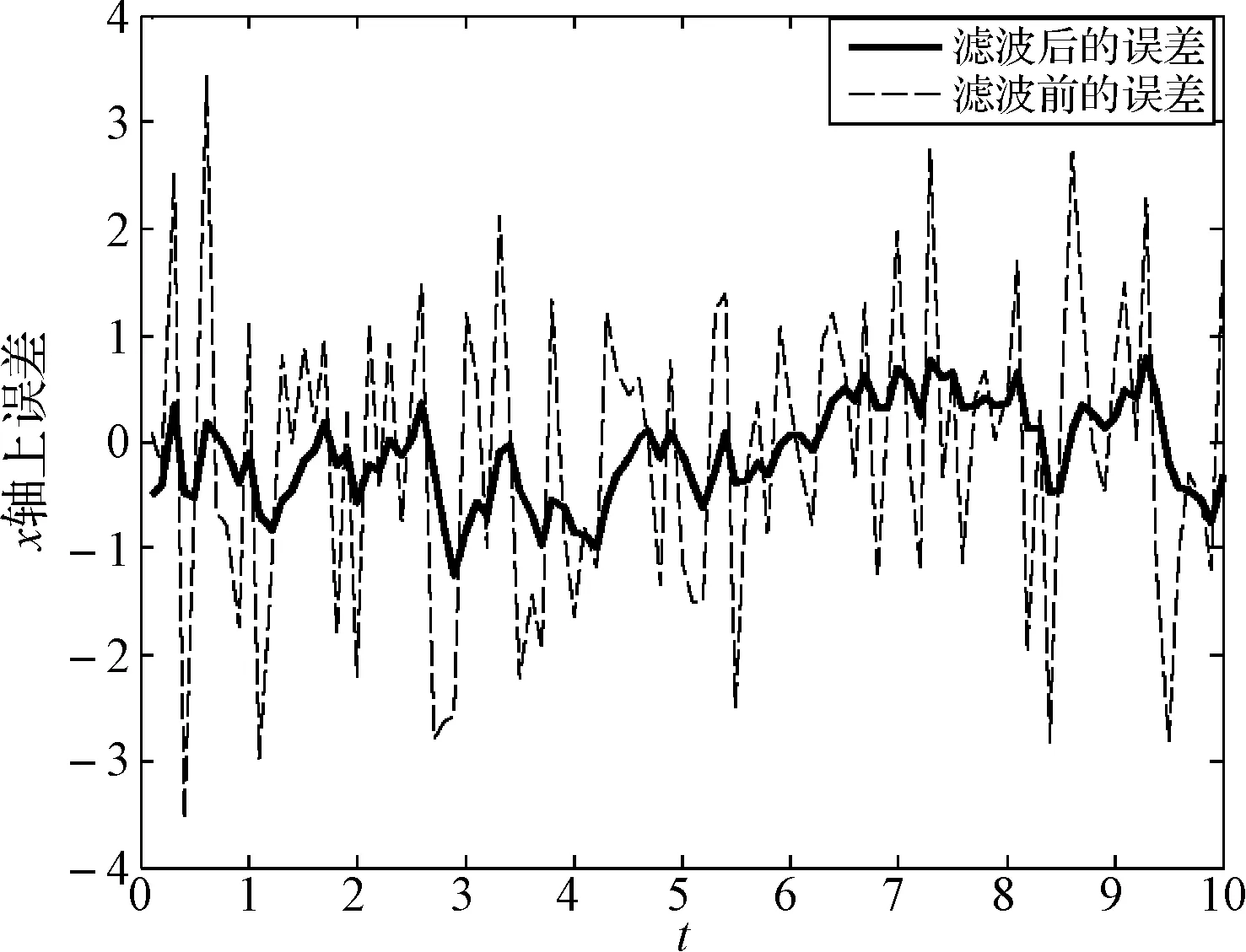
图3　卡尔曼滤波前后x方向的误差图

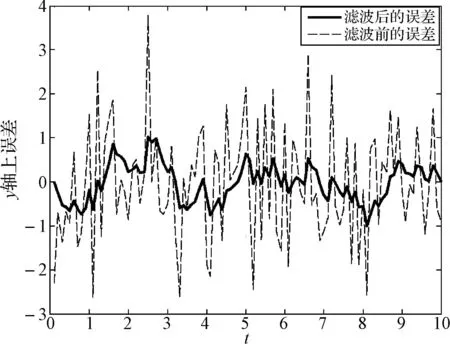
图4　卡尔曼滤波前后y方向的误差图

可以看出测量值经卡尔曼滤波器滤波后得到的最优估计更加接近真实值，卡尔曼滤波器能更加有效地减小定位误差。

5结语

通过建立系统运动的状态转移方程以及测量方程，采用卡尔曼滤波器对系统定位的测量值进行优化处理，得到系统状态的最优估计。最后的仿真算例结果表明，卡尔曼滤波在动态滤波精度上有明显改善，对动态定位有明显优化效果，从而说明卡尔曼滤波算法具有一定的有效性和实用性。

参 考 文 献

[1] 彭宇,王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报,2011,25(5):389-396.

[2] 殷桂华,王小辉,雷毅谈.基于TDOA的室内运动目标双曲线RFID定位方法[J].计算机应用,2014，34(S2):52-54.

[3] 刘华辰,刘丽莉,王奉章,等.基于TDOA测距模型的SOCP和Taylor混合定位方案[J].激光杂志,2015,32(2),107-112.

[4] 刘继斌,刘培国,李高升,等.三维AOA /TDOA被动定位及其迭代融合算法[J].全球定位系统,2006(4):5-9.

[5] 张怡,张亮,廉保旺.差分GPS定位系统的卫星位置算法研究[J].弹箭与制导学报,2003(1):85-87.

[6] 牟聪,王伟,张明. 差分 GPS 应用于机载雷达精度统计的方法研究火控雷达技术[J].2012(3):25-28.

[7] 杨世学,刘宇明.高精度差分GPS技术在海洋资源调查中的应用[J].南海地质研究,2002:92-96.

[8] 王甫红.高精度星载GPS实时定轨卡尔曼滤波模型[J].武汉大学学报,2010(6):653-656.

[9] Kalman R.E.A new approach to linear filtering and Predietion Problem[J].Jornal of Basic Eng(ASME)，1960,82D:95-108.

[10] Jens G.Balchen,Nils A.Jenssen etc.A dynamic positioning system based on Kalman filtering and optimal contral[J].Identification and control,1980(3):135-163.

[11] 梁民赞,陆扬,周新鹏.一种抑制卡尔曼滤波发散的实时数据处理方法 [J].声学技术,2008(5):761-765.

[12] 戴革林,李珺.基于混合卡尔曼滤波的组合导航算法研究[J].网络安全技术与应用,2014(10):60-63.

[13] 崔平远,郑黎方,裴福俊,等.基于卡尔曼/粒子组合滤波器的组合导航方法研究[J].系统仿真学报,2009(1):220-223.

[14] 刘爱元,戴洪德,卢建华,等.组合导航系统模拟器中的卡尔曼滤波设计[J].计算机与数字工程,2014(9):1649-1652.

Optimization of Dynamic Positioning Based on Kalman Filter

CHEN Gang1WANG Wei2DI Peng1

(1.Department of Management Science, Naval University of Engineering, Wuhan430033)(2.Department of Naval Architecture, Naval University of Engineering, Wuhan430033)

AbstractAiming at problems in the process of dynamic positioning，there are many random factors influencing positioning accuracy, Kalman filtering is applied to dynamic positioning, a Kalman filter is designed and the deviation caused by random factors is filtered to reduce the positioning deviation, the positioning accuracy is improved. Kalman filtering is one kind of linear minimum variance estimation methods. It can give the current optimal estimation of state vector with the current observation vector and the optimal estimation of last time. First, a model that objects move in the two-dimensional space is created and the transfer equation and measurement equation of the system state are given. And then the measured values is filtered. Last, the model is simulated. The results show that the Kalman filtering can effectively optimize the dynamic positioning, improve the positioning accuracy.

Key WordsKalman filter, dynamic positioning, random factors, state, optimal estimation

* 收稿日期：2015年11月11日,修回日期：2015年12月27日

作者简介：陈刚，男，硕士，研究方向：系统管理。王威，男，博士，博士生导师，研究方向：系统工程。狄鹏，男，博士，硕士生导师，研究方向：装备保障。

中图分类号P228

DOI：10.3969/j.issn.1672-9730.2016.05.015