网格剖分及边界对MT Occam反演的影响研究

钟艺文，刘　羽

(桂林理工大学 a.地球科学学院，b.机械与控制工程学院，桂林　541004)



网格剖分及边界对MT Occam反演的影响研究

钟艺文a，刘羽b*

(桂林理工大学 a.地球科学学院，b.机械与控制工程学院，桂林541004)

摘要：在大地电磁有限元模拟计算中网格剖分及边界放置是否得当，影响着最终的反演结果。基于Occam反演法从网格剖分及边界方面，设计不同模型，讨论不同网格对反演精度的影响。研究表明，对于二维介质体，只要将网格边界置于适当倍数趋肤深度的距离处，便可忽略截断边界的影响，无需放置在无穷远。在同一频段及不均匀剖分的前提下，粗细网格均可获得良好的反演结果。细网格的反演精度高于粗网格，但未能很好地圈定异常体的边界。粗网格剖分下，MT Occam法对低阻异常体反演效果较好，而对高阻异常体效果较差。

关键词：有限单元法；网格剖分；边界；MT Occam反演

0引言

有限单元法因理论完善、能模拟复杂结构等优点被广泛应用于地球物理场的数值模拟中。Coggon[1]最先将有限单元法引入大地电磁领域，经Wannamaker[2]、Rodi[3]电磁场的有限元模拟的发展与完善，有限单元法进入实用阶段。在国内陈乐寿[4]首先介绍了有限单元法在大地电磁正演计算中的应用，此后徐世浙[5]等对限单元法进行了深入研究和发展。如今有限单元法已成为二、三维大地电磁数值模拟的重要方法，但随着计算机的高速发展，人们对反演的精度要求越来越高。因此许多学者[6-8]从算法精度方面(如插值函数、线性方程组的求解)进行改进研究，而在区域剖分方面的研究相对较少[10-13]。区域剖分是插值函数选取和解线性方程组的基础，剖分是否合理所产生的误差影响远远大于算法方面计算精度的高低，即使有再高精度的求解系统，网格剖分得不合理也未必能得到合理的结果。区域剖分单元通常有四边形和三角形两种形式，前者易于剖分具有通用性，后者可以模拟复杂地形及不规则地质体。这里基于Occam反演法，区域剖分引用的是Wannamaker等[2]将矩形单元二次剖分成4个三角形网格的方案。对于网格剖分中边界的选取传统上都选择放置于无穷远处，但实际模拟区域并未能取到无穷远，所以在网格的边界处势必存在截断边界的影响。对于网格边界的选取，在追求获取高精度结果的同时还得兼顾计算时间和内存需求。作者在前人[10-14]研究基础上，同样用趋肤深度δ作为网格边界选取的依据，依次改变网格的边界，对模型的正反演计算进行比较，总结网格边界置于何处方可忽略截断边界的影响。正演是反演的基础，作者先研究网格剖分对正演的影响；在网格剖分疏密对正演影响不大的基础下，继而研究总结网格剖分对反演的影响，为后续解释工作提供依据。

1Occam反演法理论

地球物理中观测数据是有限的、离散的，同时存在观测误差，因此造成地球物理反演具有不适定性。在众多的反演方法中，Occam反演是能够克服此不足的方法之一。Constable等[15-17]提出了Occam法反演理论，Occam反演法寻求的是最光滑反演模型，因此引入了粗糙度(R)项以压制非数据产生的冗余构造。Occam反演算法在计算反演模型m的过程中，不仅要求正演响应数据与实测数据d的拟合差在设定精度内，同时要求粗糙度尽可能小。因此，使用拉格朗日乘子μ来平衡模型光滑和数据拟合程度，最终所构造的目标泛函如式(1)所示。

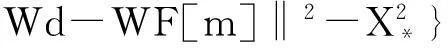
(1)

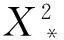
(2)

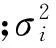
(3)

其中：Nm是模型参数个数；Npt是约束项项数。

将式(1)中的问题线性化，引用公式F[mk+△]=F[mk]+JK△,△=(mk+1-mk)表示的是模型修改量，mk是第k迭代的解，Jk为雅克比矩阵，即F[mk]相对于mk的偏导数。因此可以得到模型的迭代公式(式(4))。

mk+1(μ)=[μ(∂T∂+TT)+(WJk)TWJK]-1

(4)

2模型计算

2.1网格边界的影响

在二维结构中，在地面使用右旋制，令x轴为走向方向向北，y轴垂直x轴水平向东，z轴垂直向下。如图1所示，假设u为所要求的电磁场，在不同模式下，令上边界AB处的u都为常数“1”，值得一提的是TM模式下AB边直接取在地面，而TE模式下，为了消除地下电磁场的变化对地面电磁场的影响，AB边必须距离地面一定的距离。左右边界AC、BD应取在距横向不均匀体足够远的地方，使得在该处电磁场沿深度的分布可以被看成是与地下一维介质或均匀半空间介质时的情况相类似。对于下边界，要求异常场在CD边上的场值为“0”，CD边以下可看作是均匀半空间，所以CD边满足第三类边界条件。综合以上所讨论u满足的边界条件如式(5)所示。

(5)

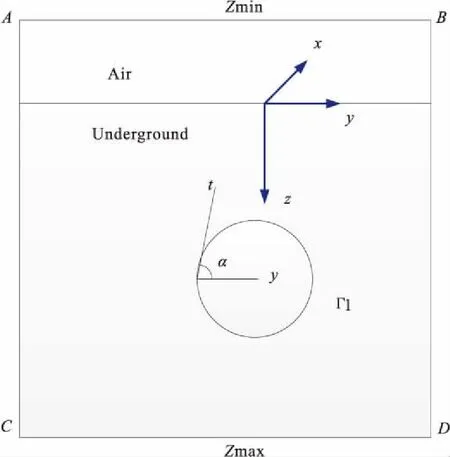
图1　研究区域及坐标Fig.1　Study area and coordinates

在做边界截取研究时，网格尺寸对计算结果有很大影响，所以在不改变网格尺寸的情况下，只对外边界做调整。基于Wannamaker等[2]在PW2D的做法，TE模式下，将研究区域总横向距离的一半作为AB边的距离。MT Occam反演不依赖初始模型，通常取均匀半空间，电阻率取100 Ω·m。正演网格数为59(横向)×17(纵向)，Occam要求反演网格是正演网格的子集，所以正反演网格必须是对齐的。反演网格设计：横向按等间距1 000 m剖分并取两个间距作为网格单元的宽，在此基础上首尾两网格单元的宽分别由±1 km、±3 km、±9 km、±27 km、±81 km、±243 km、±729 km七个间距组成；纵向网格由地面往下除前三个是按等间距剖分外，以下的都是按常数比例增长剖分，纵向最后一层的厚度则是由多个纵向剖分间距组成。频率分别为：0.937 5 Hz，0.625 Hz，0.468 8 Hz，0.312 5 Hz，0.234 4 Hz，0.156 3 Hz，0.117 2 Hz，0.078 13 Hz，0.058 59 Hz，0.039 06 Hz，0.029 3 Hz，0.019 53 Hz，0.014 65 Hz，0.009 77 Hz，0.007 33 Hz，0.004 88 Hz，0.003 66 Hz，0.002 44 Hz，0.001 83 Hz，0.001 22 Hz。

作者采用二维异常嵌入体模型做模拟计算，模型如图 2所示。若嵌入体是低阻体，等于1 Ω·m。频率取0.390 6 Hz，取背景电阻率为100 Ω·m，依据公式可知，趋肤深度大约是8 km。按上述的网格剖分左右边界已置于足够远。根据吴娟[10]、汤井田等[9]研究，只要下边界置于1 δ距离以上，就不会影

响计算精度。因纵向剖分的层数足够多，下边界所在的地方也可以认为是足够远。二维介质没有解析解，所以认为在此边界条件下计算得的是相当精确的数值解，所以把计算得到的这组数据作为参考解。

图2　二维地质体模型Fig.2　Two-dimensional geological model

首先在以上的网格剖分为基础，将正演网格的左右边界分别置于120 km、40 km、24 km处。在测点O处观测得到的视电阻率如表1所示。

表1　两侧边界变化下视电阻率观测结果Tab.1　Apparent resistivity result when changing the both sides of mesh boundary

注：R120、R40、R24分别是左右边界置于120 km、40 km、24 km处观测的视电阻率；ε为误差百分比。

从表1可知，TE模式下，当网格边界从1 000 km外不断缩减到120 km处时，所观测到的视电阻率没有变化。当缩减至40 km(5δ)、24 km时，相对高频所观测到的视电阻率的相对误差在1 %左右。随着频率继续减小，相对误差增加到了5%左右。对TM模式作了相关研究，发现不管边界取在120 km还是40 km或者24 km处，所观测到的视电阻率相对误差都维持在小于1 %的数量级。以上实验表明，只要将两侧边界置于5 δ以上的距离处，便可以当作不受截断边界影响。虽然在相对低频处会存在一些小的偏差，但整体上可以反映浅部及深部的电性分布信息。

其次，在正演网格数59(横向)×17(纵向)基础上，反演网格数为24×9+13×3，两侧边界分别置于120 km、40 km、24 km处，研究边界的选取对反演结果的影响。

Occam反演所寻求的目标拟合差是“1”，反演规定的最大迭代次数是20次。由表2的数据可知，反演的最终拟合差精度都相当高，但是Occam反演结果寻求的是最光滑模型，所以还得考虑粗糙度这方面。随着左右边界的位置不断拉近，反演模型的粗糙度会逐渐增加，反演不能正常收敛，以至于反演的迭代次数都达到限定次数时反演才结束，因此就会增加反演时间。综合上述讨论，截断边界对正反演结果都有一定的影响，左右边界都应取在大于5δ距离处，但也无需置于无穷远。

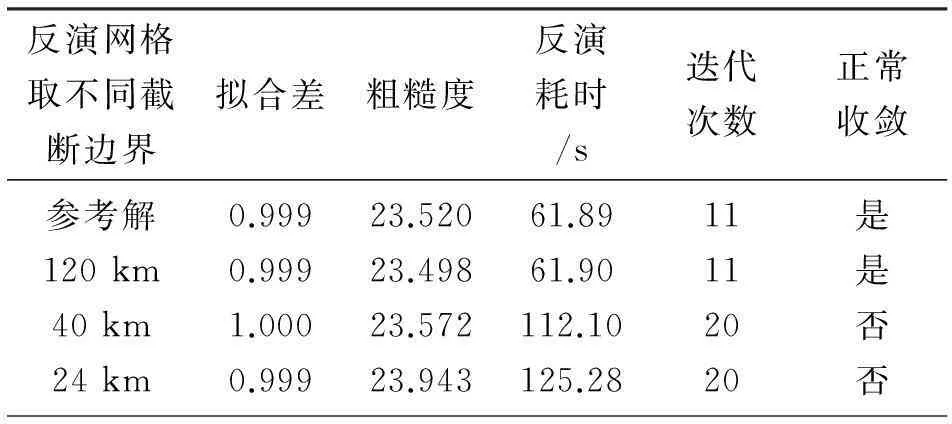
表2　反演取不同网格边界的反演结果Tab.2　Inversion results when inversion take different boundary of grid

2.2粗细网格对反演结果的影响

反演最终结果是每个单元上的电阻率值，求解方程组后将节点场值作垂向偏导，采用差分公式计算偏导数，由此可知网格剖分粗细与偏导数计算存在某种关系。以下将从网格的粗细做研究，依然采用如图2所示模型，均匀半空间中有一个矩形异常体，可取1 Ω·m或者1 000 Ω·m。网格剖分成两种形式：粗网格，正演网格数都是59(横向)×35(纵向)，反演网格数为303，测点数为21，频点数是20；细网格，正演网格数是103(横向)×35(纵向)，反演网格数为889，测点数为21，频点数是20。

反演是一个不断正演的过程，为了量化影响反演的因素，首先讨论了不同网格剖分对正演的影响。由图3可知，低阻模型的低频段粗细网格正演的数据有些许的偏差，整体上粗网格与细网格都获得基本一致的正演的结果。由此说明，只要网格横纵向剖分的尺寸在某个范围内网格剖分的疏密对正演计算影响不大。

整个研究过程使用的是MT Occam 3.0版本程序，Occam 反演需要输入四个文件，即DATA、MESH、MODEL、startup，DATA文件是经正演而产生的，Occam反演的最终结果是反演网格数个电阻率，保存在迭代文件ITERXX中，这些电阻率是地下介质的综合反映，即某种平均下的电阻率，所以会有一定偏差。使用画图程序将最终迭代文件中电阻率进行绘图便可得到图4、图5中的图形。由图4可知，不管是粗网格还是细网格在埋深5 km处都出现低阻异常，异常体中心电阻率值与实验值相差甚微，异常体中心位置都能与初始模型基本吻合，但细网格的模拟精度更优于粗网格。而左右边界方面，粗细网格异常体都未能很好的重现初始模型的边界。细网格上边界出现向上扩撒现象，而粗网格没有。粗细网格的下边界都出现异常体向下扩散延伸现象，细网格更是明显。图5是高阻模型下的反演结果，粗细网格反演的整个模拟区域都未出现明显的高阻异常现象，很难判断异常体的中心位置。出现此情况主要是由于在正演时产生的数据偏差较大加上绘图的色彩较容易混淆。结合反演数据分析可知，在原设计异常体位置处反演得出的电阻率略微的高于周边的电阻率，因此从数据方面是可以圈定异常体。

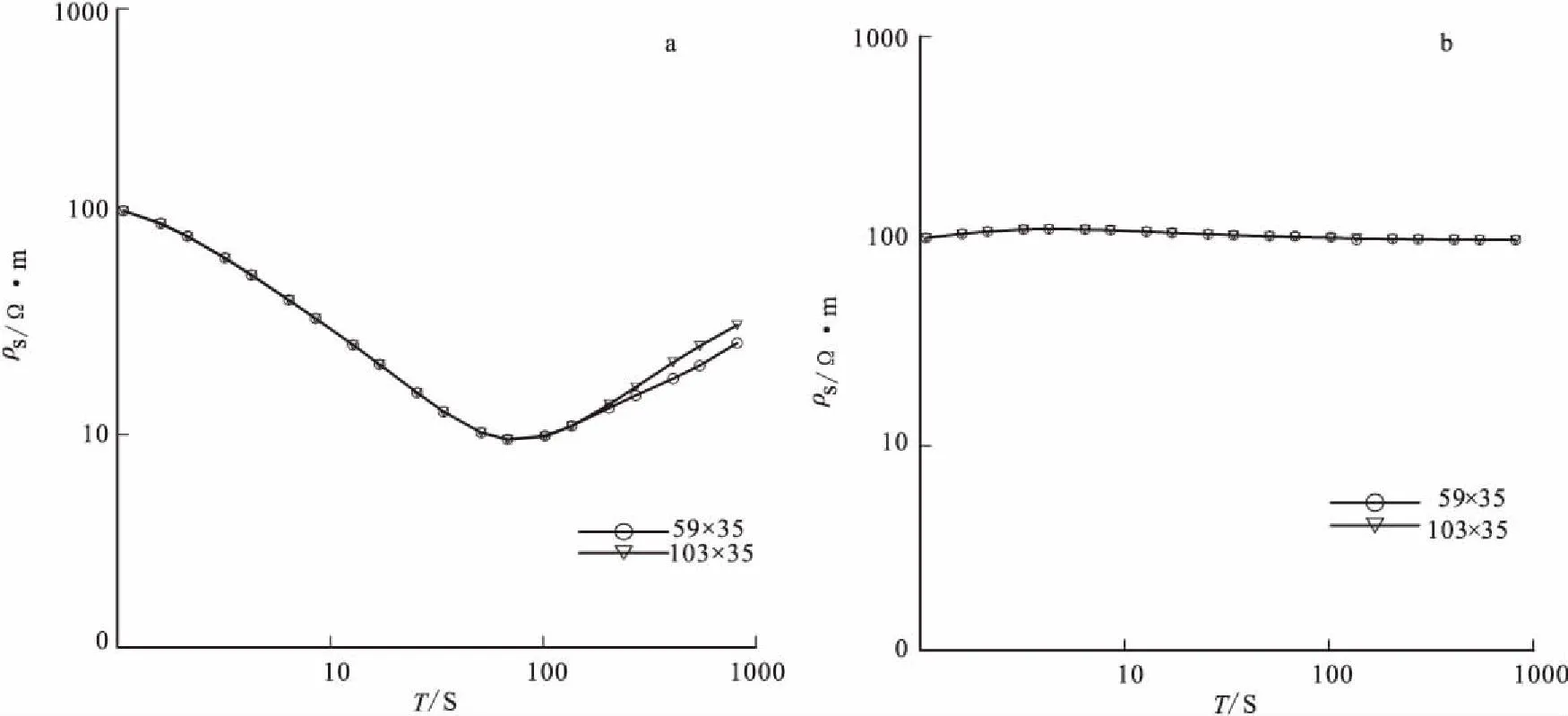
图3　不同网格下测点O的视电阻率曲线对比图Fig.3　Comparison of apparent resistivity curve at station O of different grid(a)低阻模型；(b)高阻模型

图4　低阻模型下不同网格的MT Occam反演Fig.4　The MT Occam inversion of different grid in low resistance model(a)粗网格；(b)细网格

图5　高阻模型下不同网格的MT Occam反演Fig.5　The MT Occam inversion of different grid in high resistance model(a)粗网格；(b)细网格

3结论

针对Occam框架下的MT反演问题，通过将正反演网格的边界置于不同位置，用不同反演网格作对比实验得出的结果可知：

1)用趋肤深度作为网格左右边界划分的度量，正反演网格的左右边界置于5倍趋肤深度以上但无需置于无穷远，便可忽略截断边界的影响。

2)在同一频段内，细网格的模拟精度略高于粗网格，而细网格在圈定异常体范围方面稍有欠缺。粗网格剖分下Occam反演法对低阻异常相对灵敏，反演结果精度相当高，而反演高阻异常体得的结果较差，与真实相差甚远。

3)基于浅部剖分都相对比较细，而深部则是相对较粗的不均匀剖分粗细网格两种形式都可获得良好的反演效果。

参考文献：

[1]COGGON J H.Electromagnetic and electrical modeling by the finite element method[J].Geophysics,1971,36(1):132-155.

[2]WANNAMAKER P.E，STODT J.A.A stable finite element solution for two-dimensional magnetotelluric modelling[J].Geophysical Journal of the Royal Astronomical Society，1987：277-296.

[3]RODI W L.A technique for improving the accuracy of finite element solution for magnctotelluric data [J].Geophysics，1976,44(2)：483-506.

[4]陈乐寿.有限元法在大地电磁场正演计算中的应用于改进[J].石油物探，1981,20(3):84-103.

CHEN L S.Application and improvement of finite-element method in forward calculation of geo-electromagnetic field[J].geophysical prospecting for petrole,1981,20(3):84-103.(In Chinese)

[5]徐世浙.地球物理中的有限单元法[M].北京:科学出版社，1994.

XU S Z.The finite element method in geophysics [M].Beijing:Science Press,1994.(In Chinese)

[6]陈小斌,胡文宝．有限元直接迭代算法在MT二维正演计算中的应用[J]．石油地球物理勘探，2000,35(4):487-496.

CHEN X B,HU W B.Application of finite-element direct iteration algorithm to mt 2-d forward computation[J].oil geophysical prospecting，2000，35(4):487-496.(In Chinese)

[7]马为，陈小斌.大地电磁测深二维正演中辅助场的新算法[J].地震地质，2008,30(2):525-533.

MA W,CHEN X B.A new algorithm for the calculation of auxiliary field in mt 2-d forward modeling [J].Seismology and Geology,2008,30(2):525-533.(In Chinese)

[8]柳建新，郭荣文，童孝忠，等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报，2009,40(2):484-491.

LIU J X，GUO Z W,TONG X Z,et al.Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling [J].Journal of central university，2009,40(2):484-491.(In Chinese)

[9]汤井田,薛帅.MT有限元模拟中截断边界的影响[J].吉林大学学报，2013,43(1):267-274.

TANG J T,XUE S.Influence of Truncated Boundary in FEM Numerical Simulation of MT [J].Journal of Jilin university,2013,43(1):267-274.(In Chinese)

[10]吴娟，席振铢，王鹤.网格尺寸及边界对大地电磁有限元正演精度的影响[J].物探化探计算技术，2012,34(1):27-32.

WU J,XI Z Z，WANG H.Effect of grid size and boundary on MT forward modeling using finite element method [J].Computing Technology of Geophysical and Geochemical Exploration,2012,34(1):27-32.(In Chinese)

[11]朱崇利，董云,王延平，等.网格剖分对大地电磁测深反演精度的影响[J].物探与化探，2014,38(4):737-741.

ZHU C L,DONG Y，WANG Y P，et al.The effect of grid subdivision on the accuracy of MT inversion [J].Geophysical and Geochemical Exploration,2014,38(4):737-741.(In Chinese)

[12]朱崇利.网格剖分对反演的影响[J].地球物理学进展，2014,29(2):889-893.

ZHU C L.The influence of grid subdivision on inversion [J].Progress in Geophysics,2014,29(2):889-893.(In Chinese)

[13]欧东新.计算机精度和网格大小对大地电磁有限单元法正演的影响[J].桂林工学院学报，2007,27(3):329-332.

OU D X.Effect of computer precision and grid length on MT simulating using FEM [J].Journal of Guilin Institute of Technology，2007,27(3):329-332.(In Chinese)

[14]SHARMA P S,KAIKKONEN P.An automated finite element mesh generation and element coding in 2-D electromagnetic inversion[J].Geophysics，1998,34(3):93-114.

[15]CONSTABLE S C,PARKER R L,CONSTABLE C G.Occam’s inversion:a practical algorithm for generating smooth models from electromagetic sounding Data [J] Geophysics ,1987,52(3):289-300.

[16]DEGROOT-HEDLIN C,CONSTABLE S C.Occam’s inversion to generate smooth two dimensional models from magnetotelluric data[J].Geophysics ,1990,55(12):1613-1624.

[17]DEGROOT-HEDLIN C,STEVEN CONSTABLE .Occam’s inversion and the north American central plains electrical anomaly[J].Geomag.eoelectr,1993,45:985-99.

The study of effect of mesh generation and boundary on MT Occam inversion

ZHONG Yi-wena,LIU Yub*

(Guilin University of Technology a.College of Earth Sciences,b.College of Mechanical and Control Engineering,Guilin541004,China)

Abstract:The grid subdivision is reasonable or not and the boundary select appropriately of MT modeling using finite element method have influence on the inversion results.Based on Occam inversion method,using different models from grid subdivision and boundary settings,discussed their effect to the inversion results.The result show that mesh boundary are not necessary to place at infinity only in the appropriate multiple skin depth distance can ignore the influence of the truncation boundary on two-dimensional media.At the premise of same frequency band and non-uniform subdivision,good inversion results can be obtained from both fine mesh and coarse mesh.The inversion accuracy of fine grid better than that of the coarse grid,but not good at delineating the boundary of the abnormal body.The MT Occam results of coarse grid for the abnormal body of low resistance is better,however for abnormal body of high resistance,the results is worse.

Key words:finite element method;mesh generation;boundary;MT Occam inversion

收稿日期：2015-04-22改回日期：2015-06-09

基金项目:国家自然科学基金项目(41264005)

作者简介：钟艺文(1990-)，男，硕士，研究方向为电磁数值模拟，E-mail：zhongyw321 @163.com。*通信作者：刘羽(1961-)，男，教授，博士，主要研究方向为数据处理及并行计算，E-mail：lewis_5709 @163.com。

文章编号：1001-1749(2016)02-0145-06

中图分类号：P 631.3

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.01