小学数学教学中渗透着数学化归思想
湖北省黄冈市蕲春县张塝镇孙冲小学 邓 钦
方法是数学的行为,而思想则是数学的灵魂。我们面对各种复杂多变的问题时,不会直接去处理问题,应该将它变形,将它转化为已知的问题。这样,通过化归思想的处理,我们就将各种各样复杂多变的问题简单化了。这样,学生学习的自主学习、分析问题、解决问题的能力就会提高。
一、化归数学思想转化练习教学的思维深度
练习教学是新授教学的延伸和补充,教材的安排是经过精心设计和典型的材料,在每一个看似普通的演习背后通常包含了大量的数学思想。在正常的教学教学中,教师应充分利用教材中的练习,有意识用化归培养学生的解决问题的方法。比如我们学习完乘法分配律之后,可以出这样一道题6.4×15+36×1.5,让学生将式子转化为6.4×15+3.6×15或者64×1.5+36×1.5,从而利用乘法分配律进行简便计算。
二、化归数学思想改变练习教学的呈现形式
作为数学教学的重要组成部分,练习教学中最重要的是不断发展学生的思维,培养学生良好的学习习惯。然而题海战术却被经常拿来使用,仅仅使大多数学生知道而已。但如何提高每次练习教学的思维价值,如何体验练习教学中所囊括的深层次思想却缺乏有限的思考。
小学数学先学习长方形、长方体等直线图形,而后学习圆、圆柱等曲线图形,在学习曲线图形的相关知识,可以用化归思想方法。圆面积公式的学习中,首先引导学生去学习直线图形中的矩形。然后观察它们之间的关系,每个元素的圆矩形,圆的周长的一半等效矩形的长。圆的半径等效于矩形的宽。根据矩形面积公式长乘以宽,可以得到圆的面积公式等效于圆的周长的一半去乘以圆的半径。这样,我们就根据矩形面积公式化归得到了圆的面积公式。对于圆柱的体积公式处理也可以使用化归。在求平行四边形面积公式得教学过程中,引导学生对平行四边形设法化归成矩形,然后研究它们之间的桥梁,通过对平行四边形的底等于矩形的长,平行四边形的高度等于矩形的宽度之间的联系,根据矩形的面积等于矩形的长×矩形的宽,得到平行四边形面积就等于平行四边形的底乘以平行四边形的高。这样,我们就根据矩形面积公式化归得到了平行四边形的面积公式。对于三角形的面积公式处理也可以使用同样地方法。正是基于这些问题的思考,笔者进一步拓展,去体会练习的价值,使其背后的教学理念得以展示。
三、化归数学思想丰富练习教学的探究体验
数学来自于生活,升华于生活。大多数小学数学问题是通过常见的数学模型去求解的。但在不全面的时候,数学练习是无法建立模型的,在这个时候,我们需要超越传统的思维模式去寻找解决问题的办法。唯有化归才能丰富练习教学的探究体验。
例:甲用21元买得3瓶王老吉与4瓶和其正,乙用13.5元买得1瓶王老吉与3瓶和其正,那么,每瓶王老吉与和其正价格分别多少元呢?
题中根本就没有告诉我们王老吉与和其正各自的总价以及根本就无法直接计算各自的单价。但是通过仔细观察,我们会发现:可以在题中找到两种情况下的王老吉和和其正的总价,尽管王老吉与和其正各自的单价未知数在题中无法体现,而且它们之间也没有之间的联系。虽然用二元一次方程组可以解决这个问题,但是在小学数学中属于超出的范畴。如何在小学数学范围内去处理这个问题呢?
我们尝试用加减消元化归思想去处理这个问题;具体来说就是把两组数量中的一个数量化成相等的关系,再相减,得到一个一元一次方程。分析如下:1瓶王老吉与3瓶和其正13.5元,那么可得出3瓶王老吉与9瓶和其正40.5元;题中已知3瓶王老吉与4瓶和其正21元。用40.5减去21得5瓶和其共19.5元。这样,我们可以得到和其正的单价是每瓶3.5元。接着我们可以得到王老吉的单价是每瓶3元。
学生在学习之中会遇到不同类型、不同条件下的新知识、新问题,以及利用现有的知识去解决新的知识、新的问题,还要我们学会如何培养将新知识转化为旧知识的能力。
例:饮料部门昨天销售的王老吉比和其正的3倍多5万瓶,这两种饮料一共销售了17万瓶。那么该部门分别销售王老吉与和其正多少万瓶呢?
分析如下:根据两个数量的倍数关系以及这两个数量的和或差,去求这两个数量分别是多少。题中的王老吉和和其正单价关系不属于一般的倍数关系;而是增加了王老吉比和其正的3倍还多5万瓶这样的一个条件。解析如下:17万减去5万得12万。然后可归化为:如果饮料部门昨天销售的王老吉数量是和其正的3倍,那么这两种饮料一起销售了12万瓶。这样得到和其正昨天销售了3万瓶,而王老吉则销售了14万瓶。
学生一定要学会如何使用已学的知识与研究方法去分析、解析新的知识和新的问题。学生不光要学会如何去解决问题,而且应该知道化归的过程以及如何举一反三。如下。
1.饮料商店昨天销售的王老吉比和其正的6倍少2万瓶,这两种饮料一共销售了19万瓶。那么该部门分别销售王老吉与和其正多少万瓶呢?
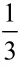
3.饮料商店昨天销售的王老吉是和其正的3倍,销售的加多宝是王老吉的3倍。这三种饮料一共销售了40万瓶。那么该部门分别销售加多宝、王老吉与和其正多少万瓶呢?
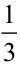
数学,让学生的实际生活引入到课堂的学习,也让学生走出课堂,走进社会大课堂,让学生体验学习数学的价值,感悟掌握数学思想方法价值。在教学中,教师要避免简单地说:“这是数学思想”。在探讨数学教学的本质中,学生会随着实践的不断深入,累积大量宝贵的经验。于是会有充分的认识:虽然遇到不同类型问题,但是处理这些问题的数学思维没有改变。化归思想作为一种重要的数学思想,面对数学问题中解决过程的普遍性,我们需要完善运用化归的思想方法去处理随时出现的复杂问题。只有这样,我们才会胜任于复杂多变的数学世界中。

