一种短期风电功率集成预测方法

张颖超，郭晓杰，叶小岭，邓 华

(1.南京信息工程大学信息与控制学院，江苏 南京 210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心，江苏 南京 210044)

一种短期风电功率集成预测方法

张颖超1,2，郭晓杰1，叶小岭1,2，邓 华1,2

(1.南京信息工程大学信息与控制学院，江苏 南京 210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心，江苏 南京 210044)

为提高短期风电功率预测精度，缩短模型训练时间，提出了一种短期风电功率集成预测方法。根据风速功率曲线和风速频率特征，将风速划分为高、中、低三段，并对每段的风速功率特征进行统计分析。高、低风速段功率波动较大，使用最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)方法可取得较高的预测精度。中风速段风速数据点较多，且风速和功率有明显的物理关系，使用高斯(Gaussian)模型预测。并用风速功率等级表对各段预测的结果进行订正，保证了算法的稳定性。用上海某风电场2014年的历史数据，验证了Gaussian模型以及高、中、低风速段对应的预测算法选取的合理性。与LSSVM预测方法相比较，集成预测方法既提高了预测精度又缩短了预测时间，适合风电场短期功率的实时预测。

短期风电功率预测；集成预测方法；Gaussian模型；LSSVM；Weibull

0 引言

风的随机性、间歇性和波动性决定了风力发电的随机性和波动性。大容量的风力发电接入电网，若调度不当，对电力系统的安全、稳定性有很大影响。准确的风电功率预测是保证电网稳定运行的关键因素之一。同时短期风电功率对未来0～72 h的发电量的预测，可为风电企业竞价上网提供帮助。因此，短期风电功率预测对电力系统的调度、生产和维护有十分重要的意义[1]。

短期风电功率预测方法，可综合概括为统计方法、物理方法和人工智能方法以及以上三种方法的组合[2-3]。而短期风电功率预测又可划分为风速、风向等气象要素的预测和风到功率的转换。常用统计方法、人工智能方法以及二者的组合来预测功率。如滑动平均自回归法[4]、马尔科夫链[5]、人工神经网络[6-7]、支持向量机[8]等单一方法实现风电功率的预测。理想情况下，风到功率转换有确定的物理规律，但在现实情况下，由于受风速风向、空气密度、尾流效应、风机自身状态等客观因素的影响，使风到功率的转换关系较难准确地刻画。为解决单一方法的不足，相空间重构、小波分解[9]、粒子群算法(PSO)[10-11]、经验模态分解(EMD)[12-13]等算法被引入。文献[10]为克服支持向量机依赖人为经验选择学习参数的弊端，引入粒子群算法优化支持向量机参数；文献[12]针对风速序列随时间、空间呈现非平稳变化的特征，提出基于EMD和极限学习机的组合预测方法。上述算法在预测精度上都有较大的提高，但在算法的效率上考虑较少。同时，上述文献都未考虑不同范围的风速和其对应发电功率之间的变化关系。

基于此，本文将统计方法和人工智能方法组合，提出一种短期风电功率集成预测方法。对风速功率曲线进行分析，风速功率曲线呈类S形，如图1所示，在S形曲线的两端随着风速的增加，功率缓慢增加，而在S形中间，随着风速的增加，功率呈现较快的增长趋势。而用Weibull概率密度函数拟合风速频率时，风速频率较大的风速大部分位于S形风速功率曲线的中间段，如图2所示。因此，本文将风机的额定风速和风速的Weibull分布的均值与其一倍标准差的差值作为风速的分割点，将风速划分为低风速段、中风速段和高风速段，并根据各个风速段的特点选择不同的模型。依据此，本文提出了Gaussian模型和LSSVM相结合的集成预测方法，与LSSVM预测方法相比，该方法既提高了预测精度又明显缩短了预测时间。

1 风电功率集成预测方法

1.1 风速功率等级表和风速功率曲线

本文研究的风机的切入风速3 m/s，额定风速12 m/s，切出风速25 m/s，额定功率2 MW，扫风面积6 793 m2。本文数据来源于上海某风电场2014年30台风机的实际发电功率和风机监测系统采集的风速、风向数据，时间分辨率为2 h，以及2014年全年的测风塔数据，时间分辨率为10 min。为描述风速和功率的对应关系，本文提出了风速功率等级表的概念。风速功率等级表，即针对同一型号风机，风速和输出功率所构成的表。风速功率等级表的构建方法如下：

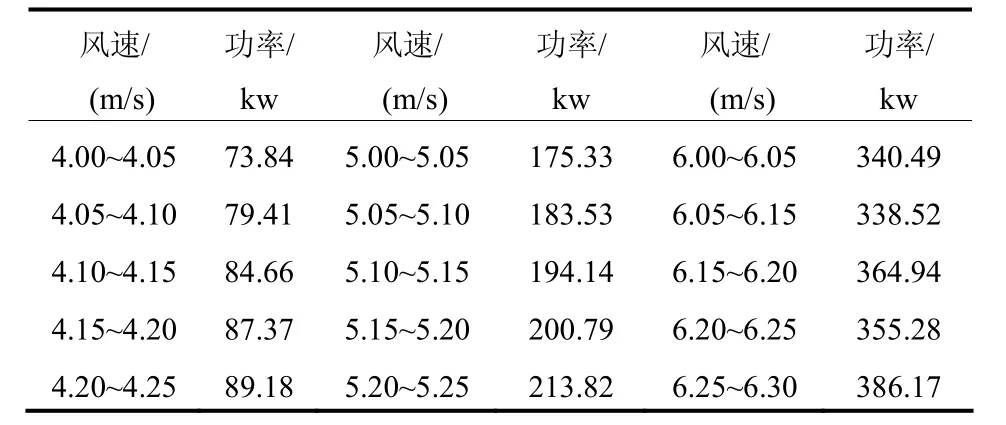
表1 风速功率等级表Table 1 Level table of wind and power

本文通过建立风速功率等级表绘制风速功率曲线。使用2013、2014年全年风速功率数据分别建立风速功率等级表。可得风速功率曲线，如图1所示。图2为风机实际工作时，风速和功率的散点图。

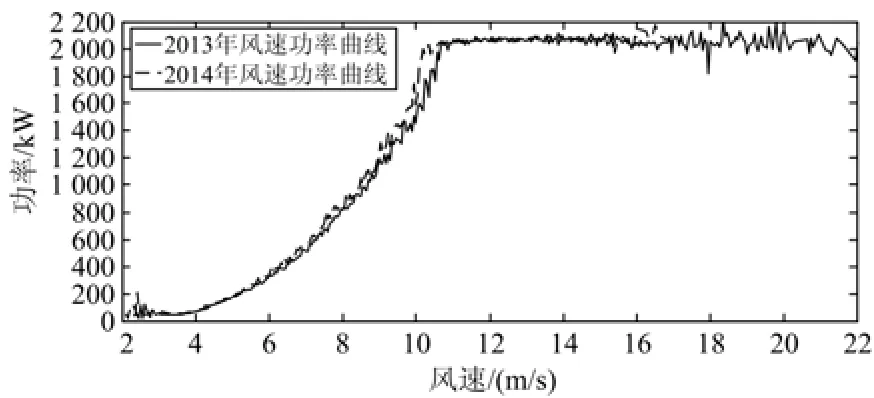
图1 风速功率曲线Fig. 1 Curves of wind and power

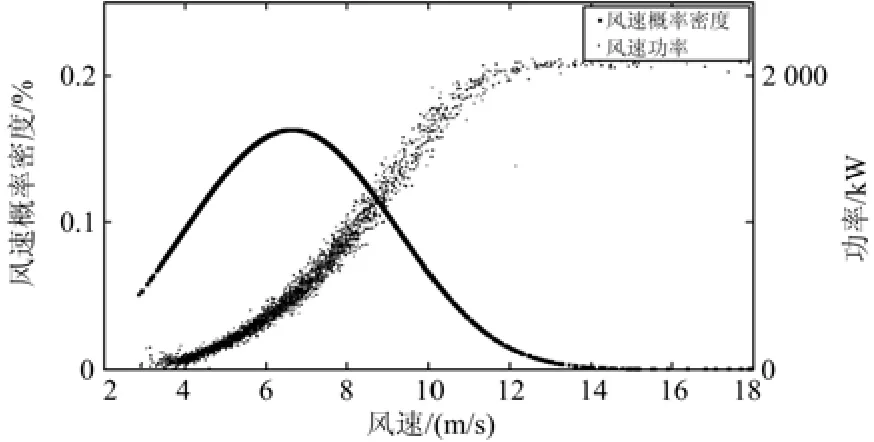
图2 风速概率密度和风速功率散点图Fig. 2 Scatters of wind power and wind probability density

1.2 Weibull分布及风速分段的划分

Weibull分布的曲线族广泛地应用于统计分析，在风能分析中它常用于拟合风速的概率密度函数[14]，其概率密度函数为

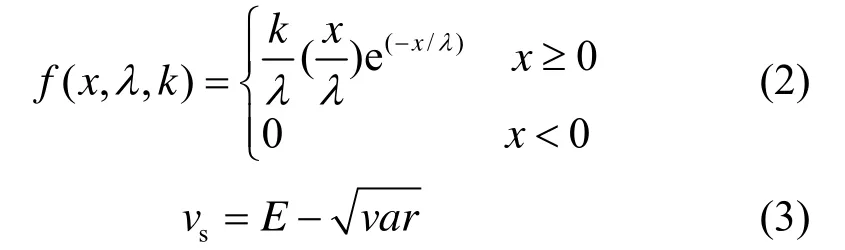
其中：x是随机变量；0l>是比例参数；0k>是形状参数；E，var分别表示均值和方差。

式(3)中sv是Weibull分布的均值E向左延伸一倍标准差之后的值，分别表示风机的切入风速、额定风速和切出风速，单位为示低风速段、中风速段和高风速段。均值E向左延伸一倍标准差后，可保证大部分的风速数据落在即图中风速段内。在该范围内的风速使用Gaussian模型预测功率，既可保证预测精度，又可有效地缩短模型训练时间。范围内的风速，即高、低风速段风速，对应的功率波动较明显，不宜使用Gaussian模型拟合，使用LSSVM方法，可获得较好的预测精度。同时，不同的训练数据，通过Weibull概率密度函数拟合风速频率可自动获取vs。因此本文将vs作为[vci,vs)和[vs, vr)之间的分割点。根据风机参数，本文中vci,vr, vco分别为3.00 m/s，12.00 m/s，25.00 m/s。

1.3 LSSVM方法预测功率

支持向量机适合解决具有小样本、非线性以及高纬模式识别特点的问题。根据风速功率曲线，在S形曲线两端，功率增长具有一定的波动性，支持向量机较适合解决本文中的问题。LSSVM[15]是支持向量机的改进，它将凸二次规划问题转化为求解线性方程组的问题，提高了求解问题的速度和收敛精度。因此本文使用LSSVM对高、低风速段的风速进行功率预测，并将风速、风向以及发电风机台数作为LSSVM的训练特征。

LSSVM由Sunken在文献[16]中提出，将支持向量机的不等式约束改成等式约束，并将误差平方和损失函数作为训练集的经验损失，于是就把解二次规划问题转化成了求解线性方程组的问题。根据结构化风险最小原理，LSSVM回归问题可以表示为以下约束优化问题。

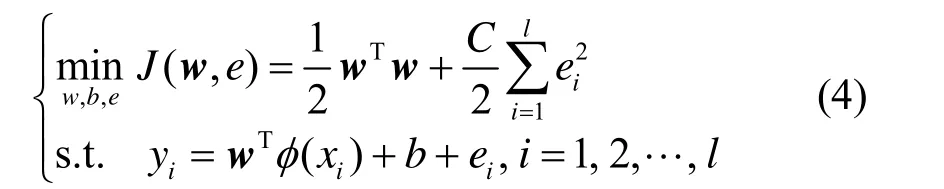
式中：ie为松弛变量；C为正规划参数，为求解上述优化问题，把约束优化问题变为无约束优化问题，引入拉格朗日函数：

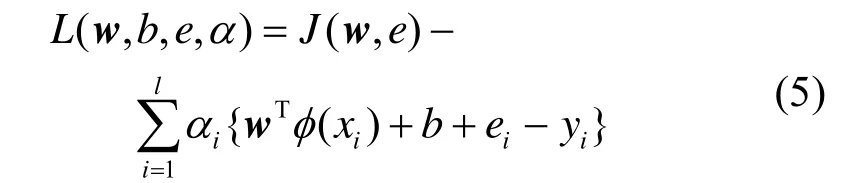
根据KKT条件求得回归函数，即LSSVM的输出为

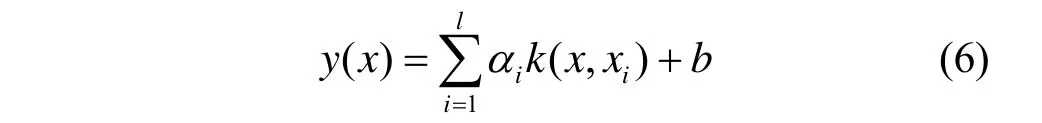
其中，k( x, xi)为核函数，由式(6)可以知，LSSVM的训练问题回归结为一个线性方程组的求解问题。

1.4 Gaussian模型预测功率

Gaussian模型就是用高斯概率密度函数精确地量化事物，将一个事件分解为若干基于正态分布曲线形式的模型，其表达式为

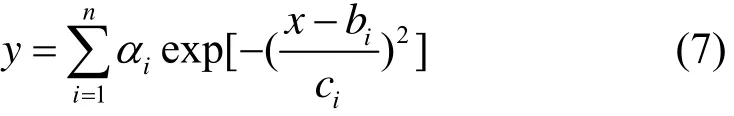
式中：ai, bi, ci均为待定系数；n为多项式的项数，本文中取n=1；x代表风速；y代表对应的功率；本文中的系数ai, bi, ci通过极大似然估计求得。由图1可知在中风速段[vs, vr)，风速功率波动较小，对应关系明显，因此本文通过Gaussian模型对[vs, vr)段风速进行拟合，并预测功率。

1.5 集成预测方法

根据以上分析，针对三个风速段特点，分别使用不同的预测方法。在中风速段[vs, vr)，只考虑风速的影响，使用Gaussian模型进行预测。在低风速段[vci,vs)和高风速段[vr, vco)，使用LSSVM方法预测。大于vco和小于vci的风速，功率置零。风电功率集成预测模型如式(8)。

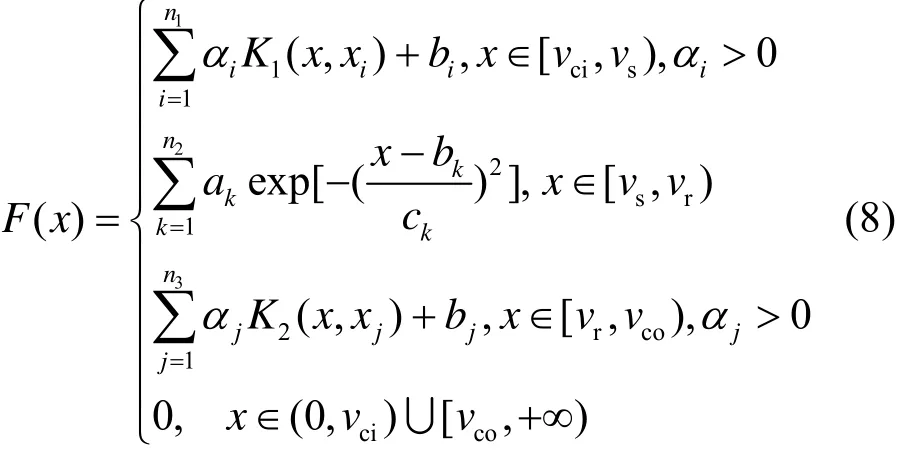
F( x)为风电功率集成预测模型。其中：n1, n3分别为在 [vci,vs)，[vr,vco)范围内用LSSVM训练时获得的支持向量的个数；K1,K2为对应的核函数；分别为对应的系数；n2为Gaussian模型的阶数；ak,bk,ck为Gaussian模型的参数。为避免因噪声数据或某一段训练数据较少，导致模型的预测误差偏大的现象，本文通过风速功率等级表，计算F(x)输出的功率的平均相对误差(MRE)，对MRE超过设定阈值的功率进行订正，MRE的计算公式如式(9)所示。

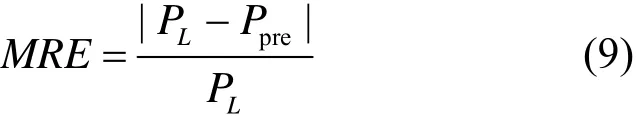
其中：LP为风速在风速功率等级表中对应的功率；Ppre为F(x)预测的功率。

2 实验验证

本文通过以下三种指标来评价预测误差[17]，分别是均方根误差(RMSE)、绝对平均误差(MAE)和平均相对误差(MRE)，其中，RMSE用来衡量误差的分散程度，MAE评价预测误差的平均幅度。MRE将绝对误差逐个与实际值进行比较，多用于电力系统负荷预测误差的评价。实验过程中，按照季节将2014年30台风机数据分成春、夏、秋、冬四组，从各组数据中随机抽取20%的数据作为测试数据，剩余的80%作为训练数据。

2.1 Gaussian模型的合理性验证

设风速功率数据对为(xi,yi)，xi表示第i点的风速，iy表示第i点的功率。使用二项式模型、指数模型、傅里叶模型以及Gaussian模型拟合出的曲线如图3所示。

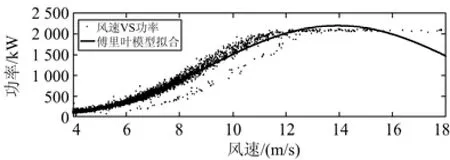
图3 各种模型拟合的曲线Fig. 3 Fitting curves of each model

表2中，二项式模型、傅里叶模型和Gaussian模型的确定系数(R-square)都在95%以上，拟合较好，但是二次模型的误差平方和(SSE)、RMSE均较大。指数模型的SSE、RMSE以及R-square三个指标都不如其他三种模型。傅里叶模型和Gaussian模型拟合结果较接近，但Gaussian模型拟合结果在SSE、RMSE以及RMSE三方面都优于傅里叶模型，因此本文选择Gaussian模型作为中风速段的预测模型。

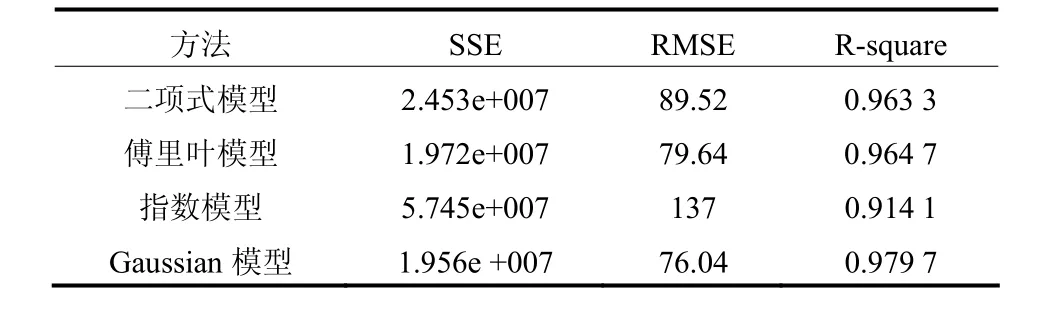
表2 各种模型的拟合结果Table 2 Fitting results of each model

2.2 各分段上预测方法选取的合理性验证

分别使用春、夏、秋、冬四组数据进行实验，实验结果如表3示所示。表3为高、中、低三个风速段分别使用LSSVM和Gaussian模型的预测结果对比，其中，L表示LSSVM，G表示Gaussian模型。从表3可知，在高、低风速段选择LSSVM的预测结果在RMSE和MAE两方面都优于Gaussian模型。而在中风速段使用Gaussian模型可以取得比LSSVM更好的预测精度。因此本文高、低风速使用LSSVM方法预测，中风速段使用Gaussian模型预测。

2.3 集成预测方法和LSSVM预测方法的结果对比

分别使用春、夏、秋、冬四组数据进行实验，比较LSSVM和集成预测方法的预测精度。实验结果如表4所示，其中T表示训练时间，单位为秒。由表4可知， 集成预测方法在RMSE、MAE上都优于LSSVM预测方法。从图4可知，集成预测方法预测误差有较明显的减少。同时，因为LSSVM在参数寻优时花费的时间较多，而Gaussian模型拟合时花费的时间较少，四次实验中集成方法的训练时间约为0.19 s，而LSSVM训练时间约为19.65 s，集成预测方法的训练时间较LSSVM有明显的减小。因此集成预测方法提高了预测精度，又缩短了模型的训练时间。

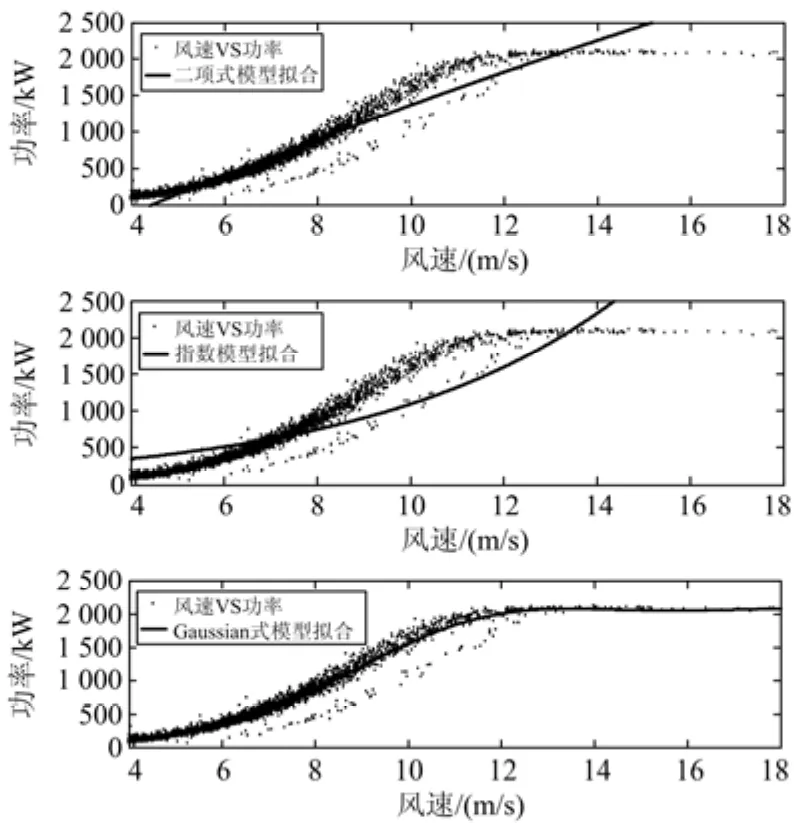
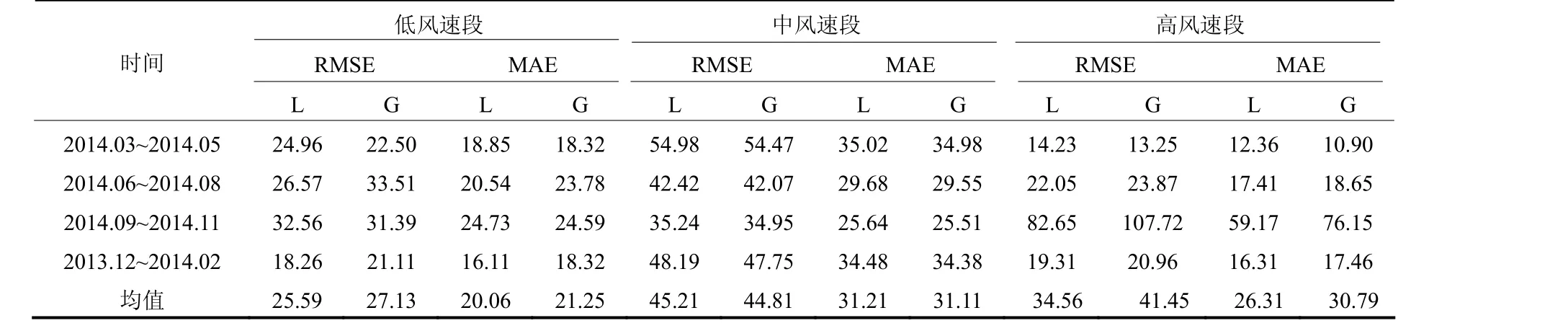
表3 各风速段预测精度对比Table 3 Comparison of prediction accuracy of each wind speed segment

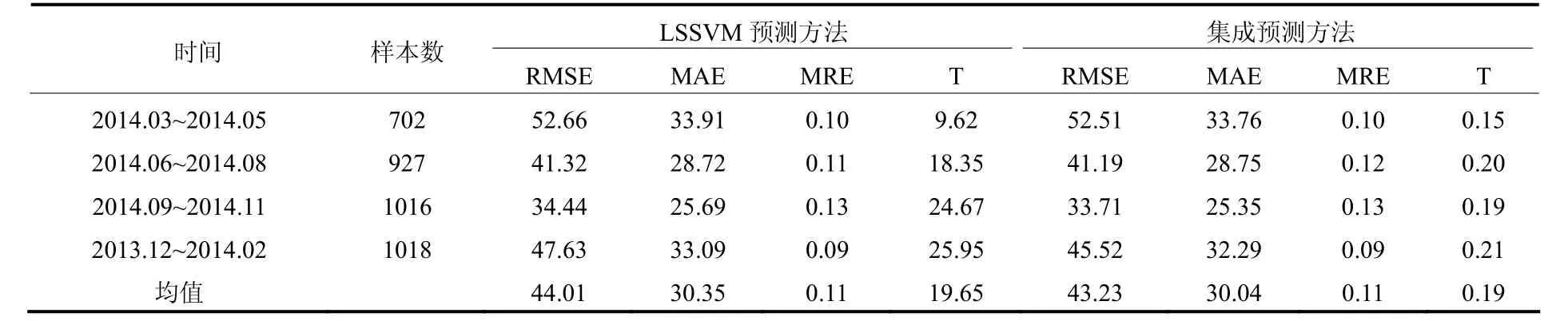
表4 两种预测方法评价指标对比Table 4 Comparative evaluation of the two forecasting methods

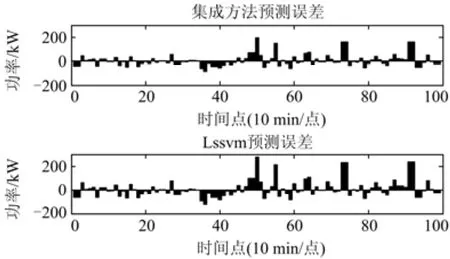
图4 集成方法和LSSVM的预测误差Fig. 4 Predicted error of LSSVM and integrated method

3 结语

短期风电功率预测是保证电网稳定运行的关键因素之一。本文根据风速功率曲线和风速频率分布的特点，分别选取风机的额定风速和风速分布的均值和一倍标准差间的差值，作为高、中、低三个风速段的分割点。在获得分段分割点的基础上，将Gaussian模型和LSSVM相结合，提出了一种短期风电功率集成预测方法。

该集成预测方法在每一个风速段上选择合适的方法进行模型的训练和预测，可以在一定程度上提高预测精度。将数据分成三部分分别训练，可以节约模型训练的时间，尤其使用Gaussian模型对中风速段数据进行拟合，可以有效地减少模型的训练时间。但是，该集成预测方法存在一定的不稳定性，当高、中或者低风速段的数据较少的时候，每个风速段对应的预测模型不能得到很好的训练，导致预测结果偏差较大。为避免这种现象，本文引入风速功率等级表，通过设定一定的阈值，对预测偏差较大的结果进行订正，保证了预测结果的稳定性。

通过上海某风电场2014年的风速功率数据，本文先对高、中、低风速段预测方法选取的合理性进行了验证，又比较了LSSVM方法和集成预测方法的预测精度和算法所消耗的时间。实验结果表明，该方法与LSSVM方法相比，既提高了预测的精度又缩短了模型的训练时间。

[1] JUNG J, BROADWATER R P. Current status and future advances for wind speed and power forecasting[J]. Renewable and Sustainable Energy Reviews, 2014, 31: 762-777.

[2] TASCIKARAOGLU A, UZUNOGLU M. A review of combined approaches for prediction of short-term wind speed and power[J]. Renewable and Sustainable Energy Reviews, 2014, 34: 243-254.

[3] FOLEY A M, LEAHY P G, MARVUGLIA A, et al. Current methods and advances in forecasting of wind power generation[J]. Renewable Energy, 2012, 37(1): 1-8.

[4] CHEN P, PEDERSEN T, BAK-JENSEN B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667-676.

[5] 周封, 金丽斯, 刘健, 等. 基于多状态空间混合 Markov链的风电功率概率预测[J]. 电力系统自动化, 2012, 36(6): 29-33. ZHOU Feng, JIN Lisi, LIU Jian, et al. Probabilistic wind power forecasting based on multi-state space and hybrid Markov chain models[J]. Automation of Electric Power Systems, 2012, 36(6): 29-33.

[6] 武小梅, 白银明, 文福拴. 基于 RBF 神经元网络的风电功率短期预测[J]. 电力系统保护与控制, 2011, 39(15): 80-83. WU Xiaomei, BAI Yinming, WEN Fushuan. Short-term wind power forecast based on the radial basis function neural network[J]. Power System Protection and Control, 2011, 39(15): 80-83.

[7] 何东, 刘瑞叶. 基于主成分分析的神经网络动态集成风功率超短期预测[J]. 电力系统保护与控制, 2013, 41(4): 50-54. HE Dong, LIU Ruiye. Ultra-short-term wind power prediction using ANN ensemble based on the principal components analysis[J]. Power System Protection and Control, 2013, 41(4): 50-54.

[8] ZENG J, QIAO W. Support vector machine-based shortterm wind power forecasting[C] // Power Systems Conference and Exposition (PSCE), 2011 IEEE/PES, IEEE, 2011: 1-8.

[9] 肖迁, 李文华, 李志刚, 等. 基于改进的小波-BP 神经网络的风速和风电功率预测[J]. 电力系统保护与控制, 2014, 42(15): 80-86. XIAO Qian, LI Wenhua, LI Zhigang, et al. Wind speed and power prediction based on improved wavelet-BP neural network[J]. Power System Protection and Control, 2014, 42(15): 80-86.

[10] 陈道君, 龚庆武, 金朝意, 等. 基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测[J]. 电网技术, 2013, 37(4): 974-980. CHEN Daojun, GONG Qingwu, JIN Zhaoyi, et al. Shortterm wind power prediction based on support vector regression machine optimized by adaptive disturbance quantum-behaved particle swarm optimization[J]. Power System Technology, 2013, 37(4): 974-980.

[11] 董红, 石连生, 赵鹏程, 等. 运用PSO-LSSVM模型的城市供电可靠性预测[J]. 电力系统及其自动化学报, 2014, 26(7): 82-86. DONG Hong, SHI Liansheng, ZHAO Pengcheng, et al. Reliability prediction of urban power network based on PSO-LSSVM model[J]. Proceedings of the CSU-EPSA, 2014, 26(7): 82-86.

[12] 张翌晖, 王贺, 胡志坚, 等. 基于集合经验模态分解和改进极限学习机的短期风速组合预测研究[J]. 电力系统保护与控制, 2014, 42(10): 29-34. ZHANG Yihui, WANG He, HU Zhijian, et al. A hybrid short-term wind speed forecasting model based on ensemble empirical mode decomposition and improved extreme learning machine[J]. Power System Protection and Control, 2014, 42(10): 29-34.

[13] 王新, 孟玲玲. 基于EEMD-LSSVM的超短期负荷预测[J]. 电力系统保护与控制, 2015, 43(1): 61-66. WANG Xin, MENG Lingling. Ultra-short-term load forecasting based on EEMD-LSSVM[J]. Power System Protection and Control, 2015, 43(1): 61-66.

[14] GHOSH S K, SHAWON M H, RAHMAN M, et al. Wind energy assessment using Weibull distribution in coastal areas of Bangladesh[C] // Developments in Renewable Energy Technology (ICDRET), 2014 3rd International Conference on: IEEE, 2014: 1-6.

[15] ZHANG Q, LAI K K, NIU D, et al. A fuzzy group forecasting model based on least squares support vector machine (LS-SVM) for short-term wind power[J]. Energies, 2012, 5(9): 3329-3346.

[16] VAN GESTEL T, DE BRABANTER J, DE MOOR B, et al. Least squares support vector machines[M]. Singapore: World Scientific, 2002.

[17] 徐曼, 乔颖, 鲁宗相. 短期风电功率预测误差综合评价方法[J]. 电力系统自动化, 2011, 35(12): 20-26. XU Man, QIAO Ying, LU Zongxiang. A comprehensive error evaluation method for short-term wind power prediction[J]. Automation of Electric Power Systems, 2011, 35(12): 20-26.

(编辑 葛艳娜)

An integrated forecasting method of short-term wind power

ZHANG Yingchao1,2, GUO Xiaojie1, YE Xiaoling1,2, DENG Hua1,2
(1. Nanjing University of Information Science & Technology, Nanjing 210044, China; 2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science & Technology, Nanjing 210044, China)

An integrated forecasting method of short-term wind power is presented for improving prediction accuracy and shortening the model training time. Based on the characteristic of wind power curve and wind speed frequency, the wind speed is divided into high, medium and low three segments, and each wind power characteristic is analyzed. As the predicted power shows larger fluctuated statuses in segments of high and low wind speed, so Least Squares Support Vector Machine is used to achieve better prediction accuracy. Much more data can be accessed in the medium segment, and there is an obvious physical relationship between wind speed and power, so Gaussian Model is used under this sort of circumstance. At the same time, the level table of wind and power is used to revise the predicted power in each section to ensure the stability of the algorithm. The rationality of Gaussian model and selection of algorithm in high, medium and low segment is verified by using the historical data of a wind farm of Shanghai in 2014. The simulated result compared with LSSVM’S shows that the proposed algorithm can not only improve the prediction accuracy, but also shorten the model training time. It can be well used to predict short-term wind power in real-time.

short-term wind power prediction; integrated prediction method; Gaussian model; LSSVM; Weibull

10.7667/PSPC151030

2015-06-19；

2015-07-27

张颖超(1960-)，男，教授，博士生导师，研究方向为复杂系统建模与评估、气象服务效益研究、风电功率预测、气象数据质量控制等；

郭晓杰(1988-)，男，通信作者，硕士研究生，研究方向为短期风电功率预测；E-mail: gxj_workmail@163.com

叶小岭(1964-)，女，教授，硕士生导师，研究方向为最优化控制。

江苏省六大人才高峰资助项目(WLW-021)；国家公益性行业(气象)科研专项资助项目(GYHY201106040)；江苏省高校优势学科建设工程资助项目