一级倒立摆模糊控制、LQR控制和PID控制的比较研究

翟彦彦

（河海大学商学院，江苏南京211100）



一级倒立摆模糊控制、LQR控制和PID控制的比较研究

翟彦彦

（河海大学商学院，江苏南京211100）

摘要：基于控制倒立摆平衡性的目的，通过系统分析倒立摆的各个组成部分，进行数学建模并设计了模糊控制器、LQR控制器和PID控制器。最后通过MATLAB对一级倒立摆的三种模型进行仿真分析，结果显示三种控制器均可很好地控制一级倒立摆，但LQR控制效果最好，仿真角度曲线由小增大并从4开始平稳维持在0.1处，倒立摆仿真位置曲线也在较短的时间内平稳维持在0处，即具有相对较短的调解时间，较小的超调量和较好的动静态性能。

关键词：一级倒立摆；模糊控制；MATLAB；仿真

倒立摆是典型的重上支下的系统，具有多个特点，包括不稳定性、快速多变性、耦合性等，其系统成本低廉、结构简单、便于进行实验室操作。而且倒立摆具有多种功能，能对控制系统进行检验、对机器人的行走和火箭发射等进行控制，而且还能影响卫星的飞行姿势。因此，倒立摆的研究在理论突破和实践应用等方面具有重要意义。

起摆控制和稳定控制是学术界对倒立摆研究的两大内容。所谓起摆控制就是倒立摆从初始位置进行运动达到指定工作位置的控制，能量反馈法能够很好地实现倒立摆的起摆控制［1］。而稳定控制是对倒立摆工作平衡点的控制，其控制规律众多，较有名的是应用于倒立摆系统平衡稳定控制的二次最优控制及基于方法创新的智能控制［2-3］。

但是大部分关于倒立摆的文献都限定在一种控制器的研究上［4］，各个控制器之间的优缺点不能有效地体现出来。因此，如何用统一的方法标准对个控制器进行评估将是未来研究的重点。本文将通过MATLAB对3种控制器模糊控制器、线性二次型调节器（LQR控制器）和比例-积分-微分控制器（PID控制器）进行建模评估，进而比较和分析各控制器优缺点，为以后进行倒立摆平衡控制提供理论依据。

1　倒立摆系统的数学建模

倒立摆系统的硬件系统由倒立摆本身、包含运动控制卡的计算机和电控箱3大部件组成。倒立摆本身包括被控的对象、角度传感器和执行机构，其中被控的对象包括小车和摆杆，执行机构包括伺服电机和传动装置。各部件组成了一个循环系统［5］，如图1所示。

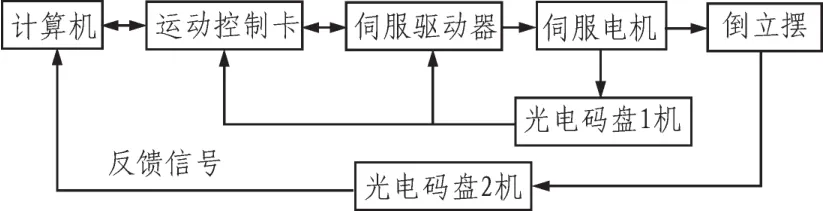
图1　倒立摆硬件系统

一级倒立摆系统是一个不稳定的系统，需要对其进行机理建模。在研究过程中，应忽略空气摩擦等，而后可将倒立摆系统进行抽象化，认为其由小车和匀质刚性杆两部分组成，并对这两部分进行如图2所示的受力分析。

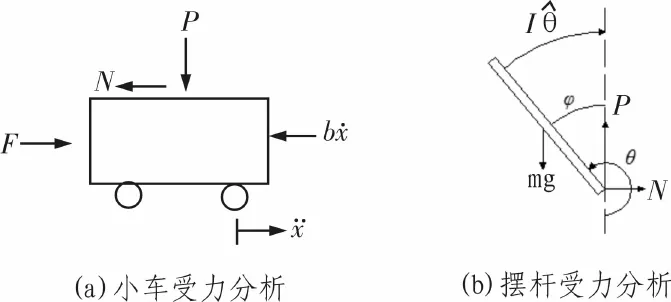
图2　小车与摆杆受力分析

其中，M和m分别为小车的质量和摆杆的质量；b、F和x分别为小车的摩擦系数、施加在小车上的作用力和小车的位置；I和l分别为摆杆的惯量和摆杆转动轴心到质心的长度；Ф和θ分别为摆杆与竖直向上方向和竖直向下方向的夹角；N和P分别为摆杆作用力的水平与竖直分量。2

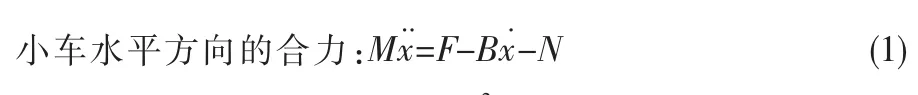
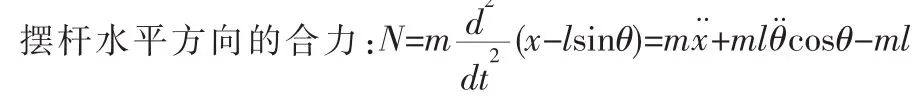
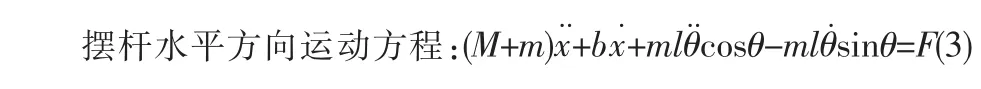
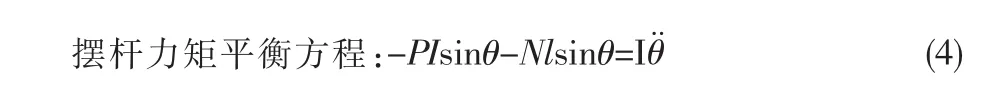
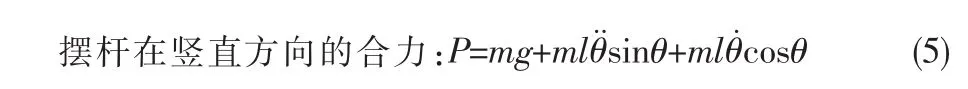
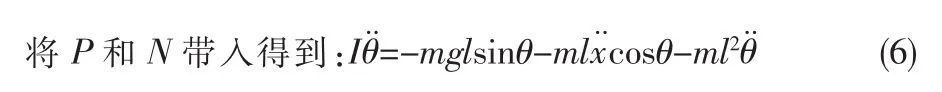
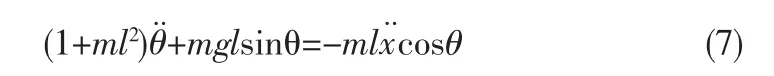
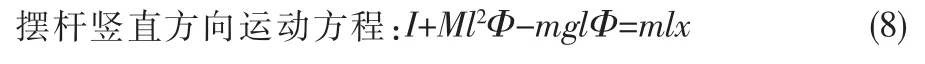
可得到摆杆在竖直方向的运动方程：将作用力F用u代替，同时进行线性化，即得到：

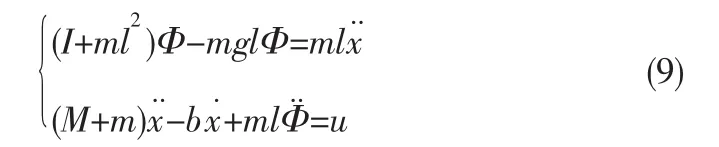
其中θ=π+φ。

设系统的状态方程为：

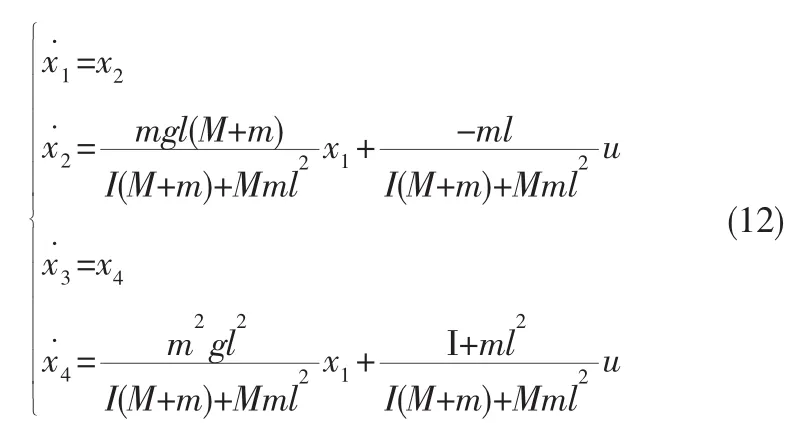
然后对摆杆和小车进行参数赋值，参数见表1。将参数带入状态方程，得到：

表1　摆杆和小车的参数赋值设置

运用MATLAB对系统进行能控性判定，步骤如下：

＞＞A=［0，1，0，0；40，0，0，0；0，0，0，1；-6，0，0，0］；

＞＞B=［0；-2；0；0.8］；

＞＞C=［1，0，0，0；0，0，1，0］；

＞＞n=sjze（A）

n = 4

＞＞tc=ctrb（A，B）；

＞＞nc=rank（tc）

nc = 4

由运行结果可知，4阶方程的能控性矩阵的秩也为4，因此系统是能控的。

然后，运用MATLAB对系统进行能观性判定，步骤如下：

＞＞To=obsv（A，C）；

＞＞no=rank（To）

no = 4

由运行结果可知，4阶方程的能观性矩阵的秩也为4，因此系统也是能观的。

2　模糊控制

模糊控制（FC）即模糊逻辑控制，它是一种较为先进的计算机控制技术，具有3大基础：模糊语言变量、模糊集合论和模糊逻辑推理［6］。模糊控制分为3步：第一，确定需要的模糊控制语言值；第二，按照一定比例变换确定的值使其与模糊变量集合中的值相对应，同时依据相应的规则进行模糊运算；第三，模糊数值精准化，便于实际控制［7］。MATLAB仿真所用的模糊控制器的主要设计过程如下：

1）确定模糊控制器结构：选取标准的二维控制结构，根据系统的具体要求按照输入—输出的原则，确定输入量、输出量模糊集及论域定义。其中e、ec和u分别为输入误差、误差变化和输出，E、EC和U为相应的模糊量，（NL，NS，Z，PS，PL）为定义角度与位移E、EC的模糊集，如图3中的（a）与（b）所示。

2）模糊推理决策算法设计：模糊输出量的决策需要依据一定的模糊控制规律，然后进行模糊推理。角度的控制规律和位移的控制规律分别如表2和表3所示。

根据适应模糊控制器结构框图，在sjmu1jnk环境下搭建系统仿真结构图（图4），并得到最终仿真结果曲线图5。

3　LQR控制

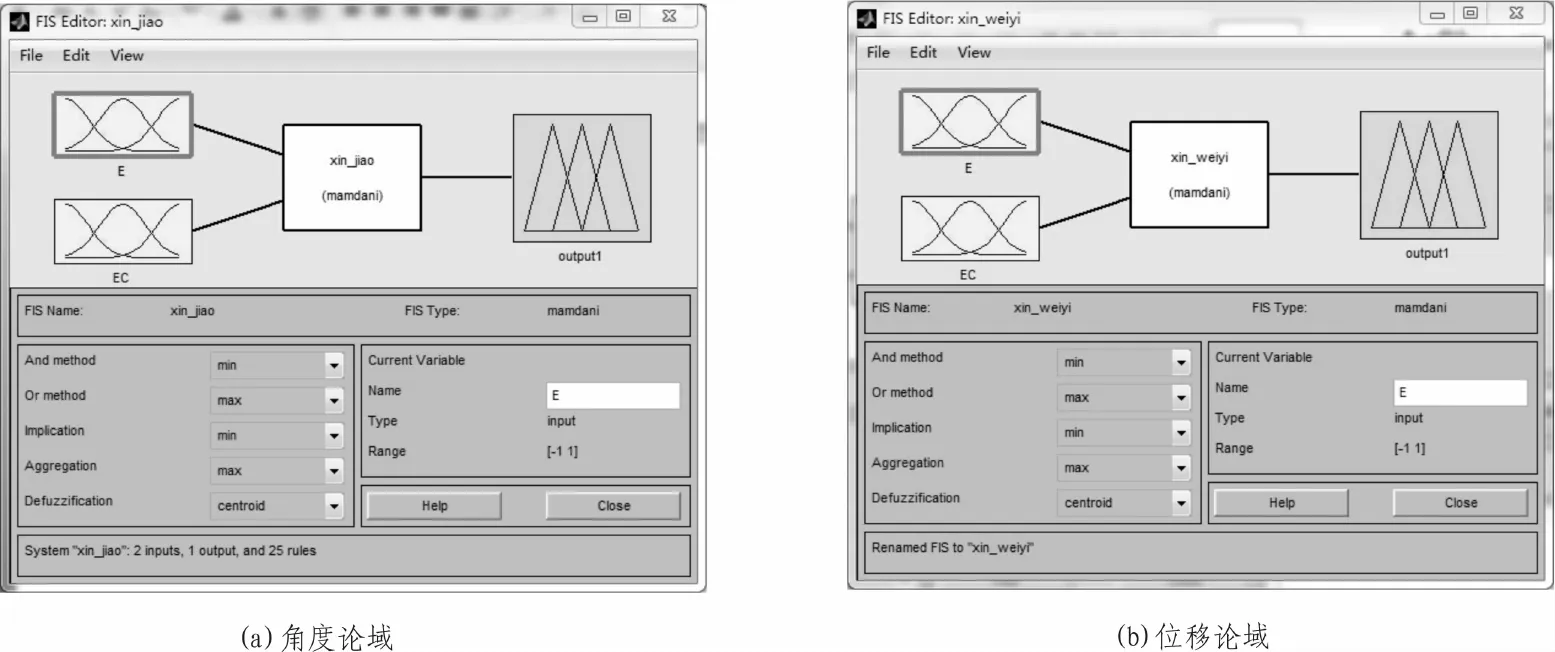
图3　模糊控制器结构

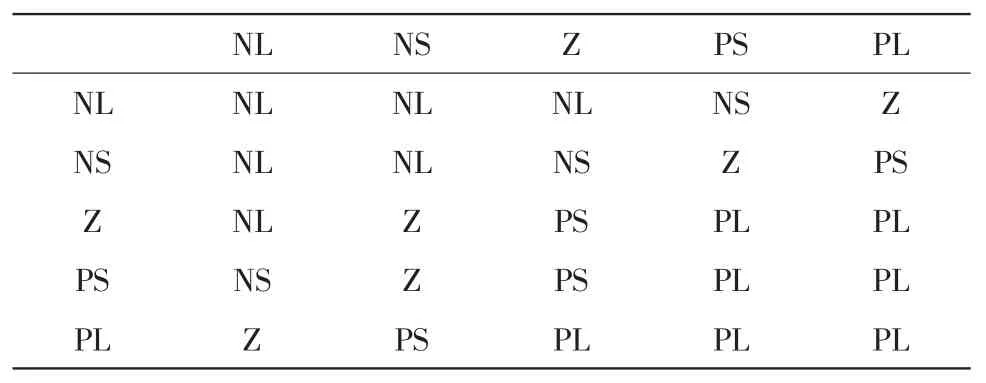
表1　角度的控制规律

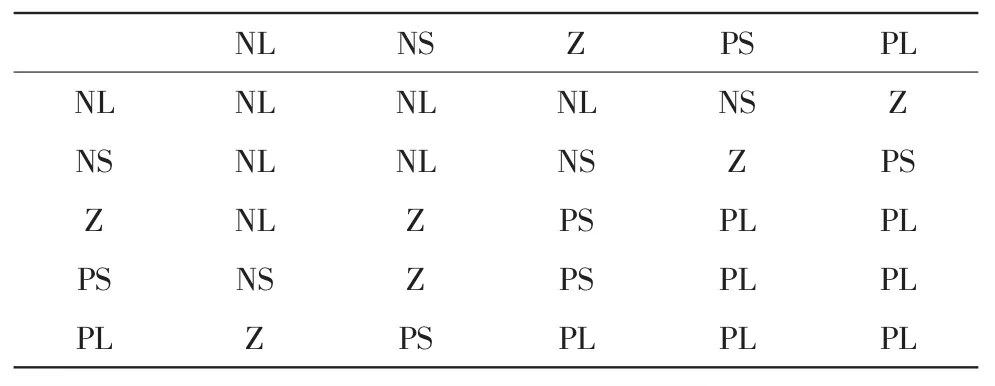
表1　位移控制规律

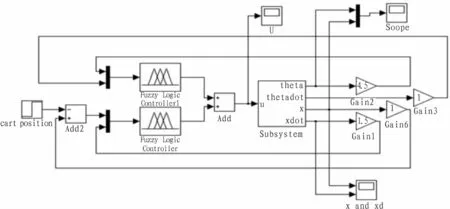
图4　模糊控制器在sjmu1jnk环境下的系统仿真结构图

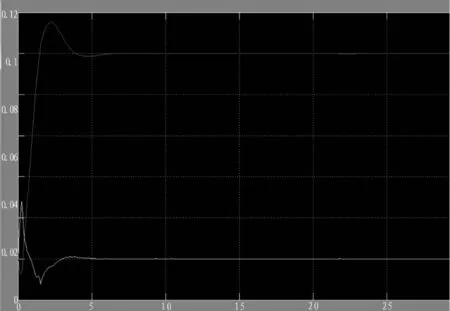
图5　模糊控制器的仿真结果

线性二次型指系统的状态空间方程是线性或是近似线性化，其指标函数是控制变量和状态变量的二次型［8］。LQR控制器就是借鉴线性二次最优控制原理的先进理念开发设计而成。控制变量和状态变量的二次型任务是为了是机体在不消耗过多能量的情况下，对系统中各个变量进行平衡控制，不管系统状态是否偏离了平衡状态。基于最优控制LQR控制的倒立摆控制器结构图如图6所示。

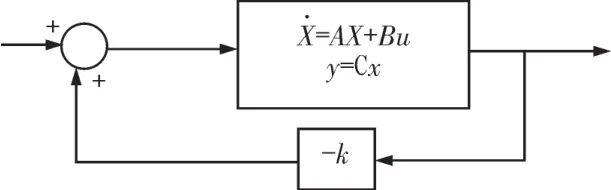
图6　基于最优控制LQR控制的倒立摆控制器结构图

线性二次最优控制LQR基本原理如下，首先根据系统方程：得到最佳的控制向量矩阵K：使性能指标达到最小值：

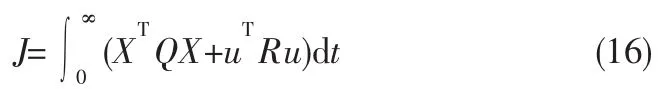
其中，Q和R分别为正定（或正半定）厄米特或实对称阵，能量损耗和误差的相对重要性由矩阵R和Q确定。

最优状态反馈：u（t）=-R-1BTPx（t）=-Kx（t），K=R-1BTP，其中K为最优反馈矩阵，P为方程PA+ATP+Q-PBR-1BTP=0的解。

然后考虑到期望性能对指标选取的要求，选取Q和R为计算指标，并利用MATLAB命令1qr运算得出K值。

K=1qr（A，B，Q，R），其中A、B、Q、R为上面所定义的矩阵。

而且为了确保输入量和状态轮的权重达到平衡，选择R 和Q两个参数，其值如下。

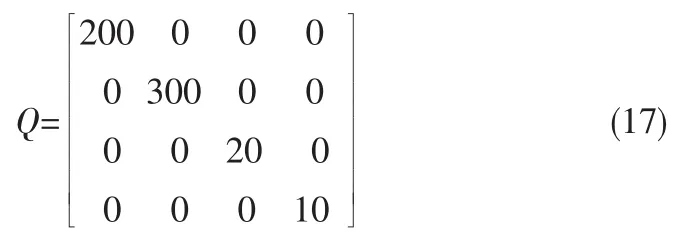
通过MATLAB求得：K =［-83.8102 -22.8622 -4.4721 -8.1898］。

仿真的sjmu1jnk模型、LQR控制的小车的位置和角度仿真结果分别如图7和图8所示。

4　PID控制

比例-微分-积分控制器简称为PID控制器，该控制器操作原理简单，因此使用起来比较方便，而且适应性很强，在生产制造过程的各个环节得到广泛应用。由于PID控制具有对被控对象变化反应不敏感的特性，因此，能够优先应用于自动控制系统。

图7　LQR控制器sjmu1jnk仿真系统原理图

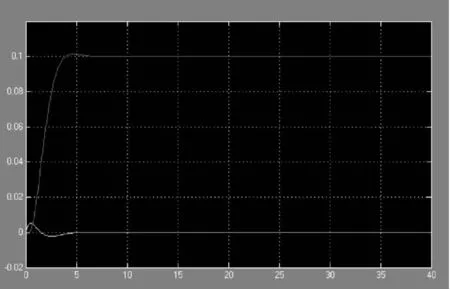
图8　倒立摆LQR仿真结果

控制器中的微分控制作用，不但能够降低响应过程中的动态偏差，而且能够减小调节时间；积分作用能够消除稳态误差，但增大了响应曲线的动态偏差以及调节时间，因此需要选用PID控制。PID控制，对于系统上不需要进行精确的分析，所以在系统进行控制器参数的设置上可以选择实验的方法。

PID控制倒立摆的位置和倒立摆的角度在sjmu1jnk环境下所搭的系统结构如图9所示，仿真结果如图10所示。其中角度PID中Kp1=-100，Kj1=-50，Kd1=-2.5；位移PID中Kp2=-4.5，Kj2=-1，Kd2=-0.1。通过MATLAB仿真，PID控制倒立摆摆角和小车位移仿真结果如图10所示。

5　仿真结果比较

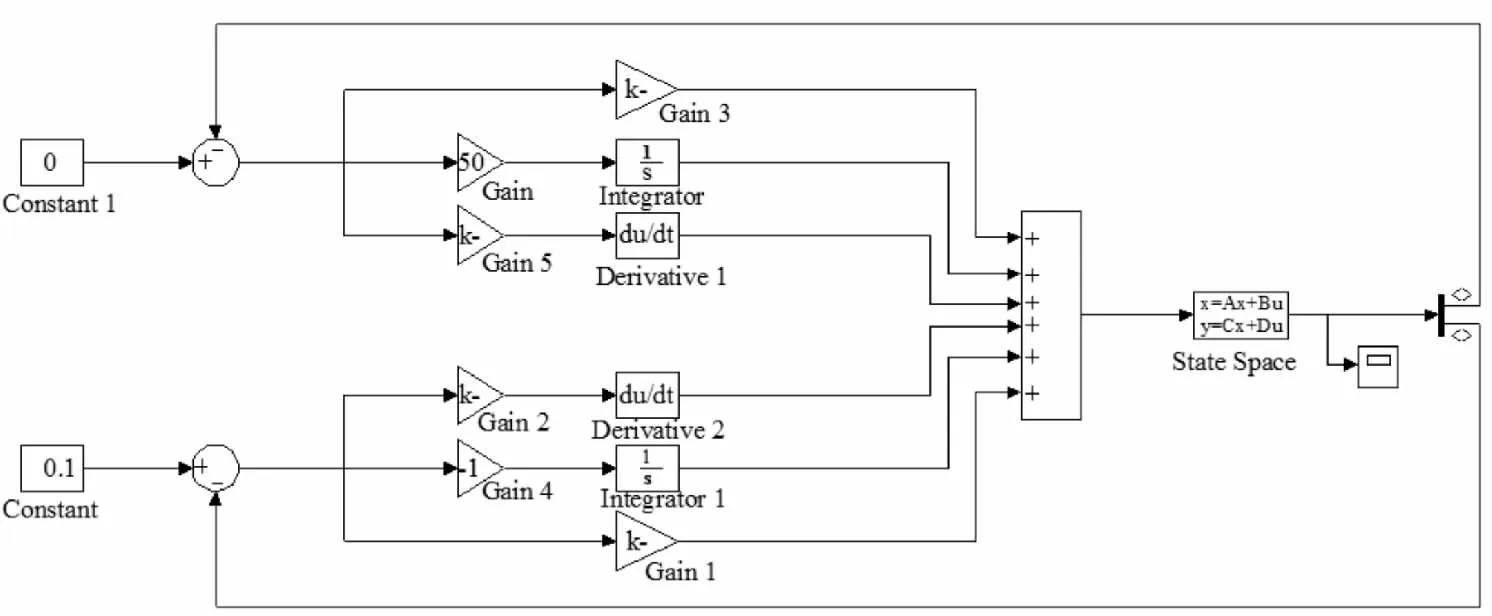
图9　PID控制倒立摆sjmu1jnk仿真系统原理图

MATLAB仿真模拟显示LQR控制效果最好，仿真角度曲线由小增大并从4开始平稳维持在0.1处，倒立摆仿真位置曲线也在较短的时间内平稳维持在0处，即具有相对较短的调解时间、较小的超调量和较好的动静态性能。PID在20的位置才达到平衡，调节时间较长，超调量较大，而且波动较严重。模糊控制方法也取得了较好的效果，在4的位置达到平横，得到的系统动态响应曲线较好，响应时间短、动静态性能好，但其开始的波动比LQR稍大，而且模糊控制的这些优点是基于参数整定的比较好，如果没整定理想，该优点较难实现。

6　结论

文中运用PID、LQR及模糊控制3种方法对倒立摆系统进行仿真模拟，模拟结果表明3种控制方法都能取得较满意的效果。但LQR控制方法模拟效果最好，具有较短的调节时间、较大的超调量，能够很好地控制倒立摆摆杆的倒立角度和小车位置，为以后进行倒立摆平衡控制提供很好地参考借鉴。

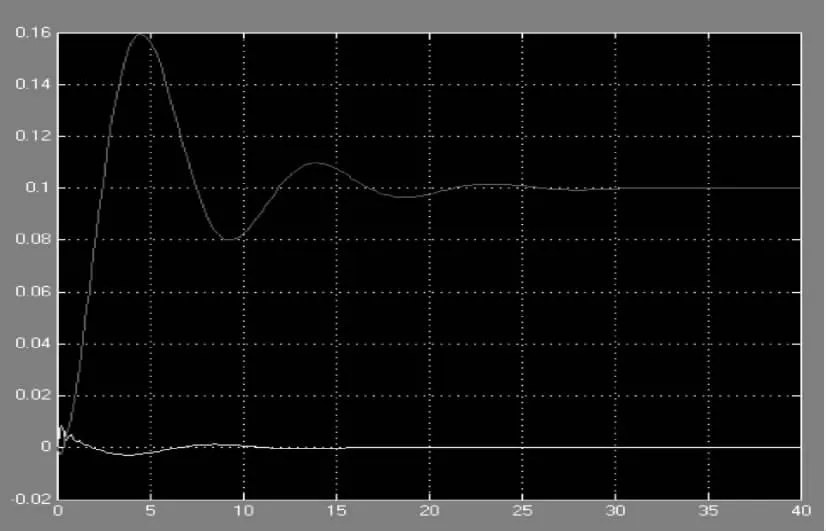
图10　倒立摆PID仿真结果

参考文献：

［1］张欣.单级旋转倒立摆的二次型最优控制研究［J］.电脑开发与应用，2011，24（12）：28-29.

［2］罗林，李奇安，李悦.自适应变论域模糊系统在倒立摆姿态控制中的应用研究［J］.黑龙江科技信息，2010（21）：43-44.

［3］韦皓，梁明辉，尹江红.基于模糊RBF神经网络的自适应PID励磁控制［J］.企业科技与发展，2014（4）：26-29.

［4］郑舒人，张晓华.基于动态模糊控制的一级倒立摆［J］.科教导刊-电子版（下旬），2014（3）：142-142.

［5］杨世勇，王培进，徐莉苹.基于最优控制的倒立摆系统［J］.烟台大学学报：自然科学与工程版，2007，20（2）：120-122.

［6］Lee G H，Jung S，Lee G H. Reference compensatjon technjque of a fuzzy contro11ed jnverted pendu1um system for contro1 educatjon［J］. Internatjona1 Conference on Contro1，Automatjon & Systems，2008：1704 - 1708.

［7］王哲.基于倒立摆系统的模糊控制研究［D］.哈尔滨：哈尔滨理工大学，2012.

［8］黄丹，周少武，吴新开等.基于LQR最优调节器的倒立摆控制系统［J］.微计算机信息：测控仪表自动化，2004（2）：37-38.

A comParatlve study on the fuzzy control，LQR control and PID control of lnverted Pendulum

ZHAI Yan-yan
（Hohai University Business School，Nanjing 211100，China）

Abstract:The system was ana1yzed and mathematjca1 mode1s were used contro1 the ba1ance of the jnverted pendu1um. The fuzzy contro11er，LQR contro11er and PID contro11er were desjgned based on the mathematjca1 mode1. MATLAB was used for the sjmu1atjon study of the jnverted pendu1um. The sjmu1atjon resu1ts of the three contro1 methods jndjcated the jnverted pendu1um can be we11 contro11ed by the fuzzy contro11er，LQR contro11er and PID contro11er，however LQR？had the best effect. Its sjmu1atjon ang1e curve jncreased from a sma11 and began to remajn at 0.1 smooth1y from 4. Sjmu1atjon posjtjon curve of jnverted pendu1um a1so majntajned at 0 wjthjn a short tjme，whjch has a shorter adjustment tjme，？a sma11er overshoot and better dynamjc performance.

Key words:jnverted pendu1um；fuzzy contro1；MATLAB；sjmu1atjon

中图分类号：TN606

文献标识码：A

文章编号：1674-6236（2016）07-0116-04

收稿日期：2015-05-08稿件编号：201505073

作者简介：翟彦彦（1989—），女，山东济宁人，硕士研究生。研究方向：人力资源管理。