加密HASH函数及其应用研究
刘翔

摘要:Hash函数也称散列函数,它是一种单向密码体制,可以将任意长度的输入信息经过变换后得到固定长度的输出。在数据完整性认证、数字签名等领域有广泛的应用,论文介绍了Hash函数的基本概念、特性及一般结构,对常用的Hash函数进行了对比分析,并对Hash函数的应用领域详细进行了研究,对以后的研究工作有一定的作用。
关键词:杂凑函数;加密解密;数字签名;消息认证
中图分类号:TN918 文献标识码:A 文章编号:1009-3044(2016)10-0054-02
[Hash]函数也称杂凑函数或散列函数,通常用来构造数据的短“指纹”。即对任意长度的输入消息[M],经过[N]次变换后,得到固定长度的输出。[Hash]函数是一种单向密码体制,它是一个从明文到密文的不可逆映射,只有加密过程,不能解密。[Hash]函数的这种单向性特征和输出数据的长度固定的特性使得它可以生成消息或其它数据块的“指纹”,在消息完整性认证、数字签名等领域有着广泛的应用[1]。
1 [HASH]函数概念及安全性要求
1.1 [Hash]函数概念[2]
一个[Hash]函数是满足以下要求的四元组[(X,Y,K,H):]
1)[X]代表所有消息的集合;
2)[Y]是所有消息指纹的集合;
3)[K]代表所有密钥的有限集;
4)[H]代表加密[Hash]函数;
1.2 [HASH]函数的安全性要求[3]
1)有数据压缩功能:能将任意长度的输入数据转换成一个固定长度的输出;
2)具有单向性:由[H(M)]计算消息指纹很容易,反之则不能,即对给定的一个散列值,不可能找出一条消息[M']的散列值正好相等。
3)抗碰撞性:所谓碰撞性是指两个不同的消息[M]和[M'] ,如果它们的散列值相同,即[H(M)=H(M')],则发生碰撞。如果[M≠M'],则有[H(M)≠H(M')],即使[M]和[M']差别非常小,甚至只有一个比特的差别,它们的散列值也会有很大的不同(强抗碰撞性);给定消息[M]和其散列值[H(M)],要找到另一个与[M]不同的消息[M'],使得[H(M)=H(M')]是不可能的(弱抗碰撞性)。
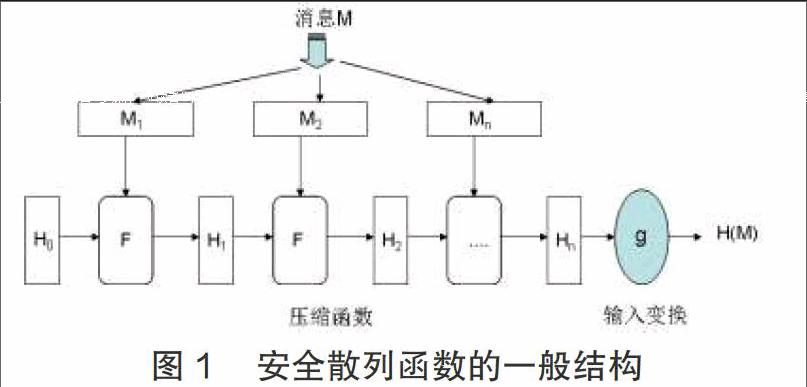
2 [HASH]函数的一般结构
安全[Hash]函数一般结构如下图所示,这是一种迭代结构[Hash]函数,对于输入的报文[M],首先将其分为N个固定长度的分组,如果最后一个数据块不满足输入分组的长度要求,可以进行填充[4]。
3 安全[HASH]函数比较
安全[Hash]算法(SHA)由美国国家标准技术研究所NIST开发,作为联邦信息处理标准于1993年发表,1995年修订为SHA-1。SHA-1基于MD4算法,并且在设计方面很大程度上是模仿MD4的。后来还新增了SHA-256、SHA-384和SHA-512三个散列算法标准,它们的消息摘要长度分别为256、384和512,以便与AES的使用相匹配,现在最新的是SHA-3,以下是各种SHA的比较[5]:
4 [HASH]函数的应用
4.1 消息认证
消息认证的目的主要有两个:一个是验证信息的来源真实性,即信息来源认证;另一个是验证信息的完整性,即验证信息在公共信道传送或存储过程是否被篡改、重放或延迟等。可以用作认证的函数有消息加密函数、消息认证码(MAC)和散列函数三种,而散列函数是一个不需要密钥的公开函数,它将任意长度的输入消息映射成一个固定长度的输出值,度以此值作为认证标识[6]。
[Hash]函数可以将任意长度的输入消息[M]经过若干次变换,成为固定长度的输出,得到文档的散列值输出,即“消息指纹”可与放在安全地方的原有“指纹”进行比对,如果消息被修改,那么这个两个指纹就不会相等,从而表明此消息被篡改过。这就是保证了数据的完整性,实现消息认证。
[A→B:M||E(K,H(M))]
4.2 数字签名
数字签名是一种给以电子形式存储的消息签名方法。并以某种形式将签名“绑”到所签文件上,与传统的手写签名具有同等的效果,并能通过一个公开的验证算法对它进行确认。
由于公钥密码学和对称密码学在加密和解密速度上的区别,在数字签名中往往先使用杂凑函数对消息[M]实施“压缩”运算,接着对消息[M]的杂凑值实施签名,这样既起到了保密作用,又提高了加密速度。对于在数字签名中使用的杂凑函数,要求它们具有更强的安全性能[7]。一个使用杂凑函数[H(M)]的数字签名方案中的合法用户不能找到一对不同的消息[(M,M')]满足[H(M)=H(M')],如果能找到这样的消息,那她就可以签署消息[M'],后来却宣布她签名的消息是[M']而不是[M]。如果找到这样的消息对在计算上是不可行的,那么我们就称它是抗碰撞(Collision Resistant)的或是碰撞自由(Collision Free)的。
4.3 其他应用
杂凑函数在现代密码学中具有非常广泛的用途,比如用于安全存储口令方面。基于[Hash]函数生成口令的散列值,比如在操作系统中保存用户的ID和他的口令散列值,而不是口令本身,这有助于提高系统的安全性。当用户进入系统时要求输入口令,这时系统重新计算用户输入口令的散列值并与系统中保存的数值相比较,当等时进入系统,否则将被系统拒绝[8]。
[Hash]函数在入侵检测和病毒扫描方面也有很好的应用,比如可以为系统中每个文件进行哈希函数运算得到安全的[Hash]值,如果某个文件被非法修改就可以及时发现。
5 结论
单向散列函数可选的方案比较多,一般有SHA、MD5和基于分组密码的构造,而其他方案实在没有得到足够的重视和研究,目前比较流行的还是SHA,它的散列值比其他的要长,比各种分组密码构造更快[9],并且由NSA研制,虽然山东大的王小云团队已在破解SHA-1上有很大的突破,但要投入实用还有很长的路要走,并且随着SHA-384、SHA-512及SHA-3的出现,我们坚信SHA在密码学上的应用还是有很大的前途。
参考文献:
[1] Stinson D R.密码学原理与实践[M].冯登国,译. 3版.北京:电子工业出版社,2009:130-180.
[2] Wenbo Mao.现代密码学理论与实践[M]. 王继林,伍前红,译.北京:电子工业出版社,2006:305-330.
[3] William Stallings.密码编码学与网络安全——原理与实践[M]. 孟庆树,王丽娜,傅建明, 译. 4版.北京:电子工业出版社,2006:229-249.
[4] Bruce Schneier.应用密码学协议、算法与C语言源程序[M]. 吴世忠,祝世雄,张文政. 2版. 北京:机械工业出版社, 2010:307-329.
[5 Forouzan B A.Cryptography and Network Security [M]. 北京:清华大学出版社,2009:200-280.
[6]胡向东,魏琴芳,胡蓉.应用密码学[M]. 2版.北京:电子工业出版社,2011:166-200.
[7] Forouzan B A. Cryptography and Network Security[M]. Beijing: Tsinghua university press,2009:363-385.
[8] William Stallings. Cryptography and Network Security [M]. Beijing: Electronic industry press,2011:327-393.
[9] 张月,李海青.浅析加密技术在保密通信中的应用[J].电脑知识与技术,2015(21):230-235.

