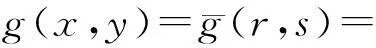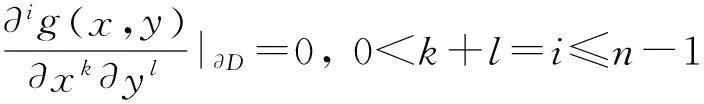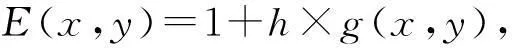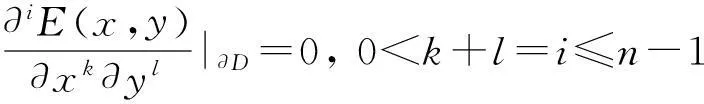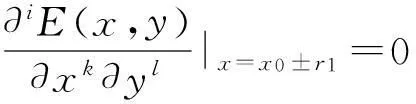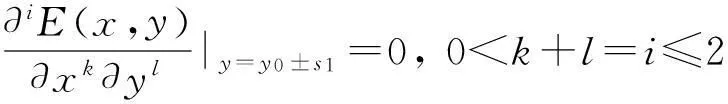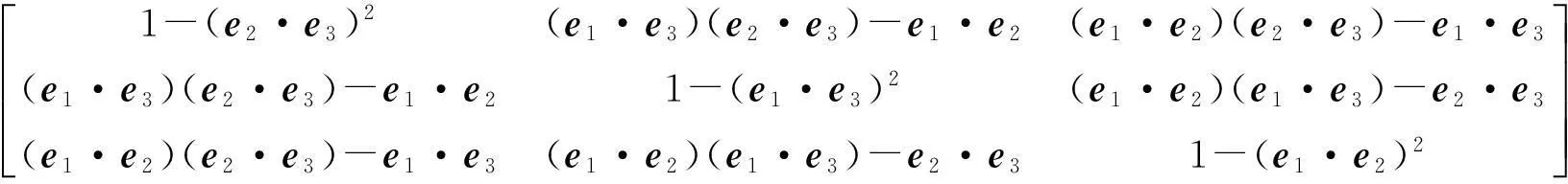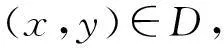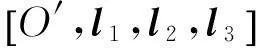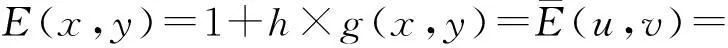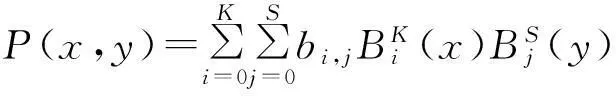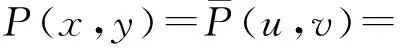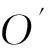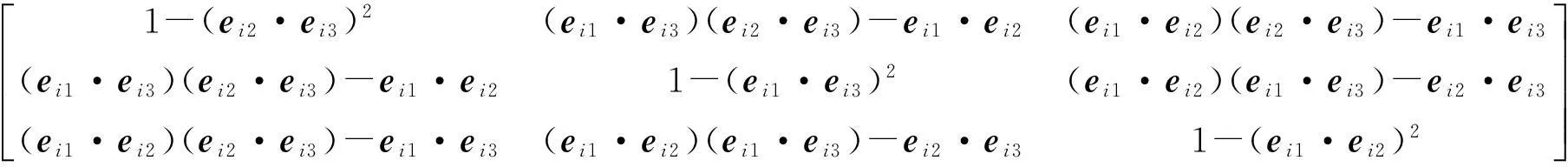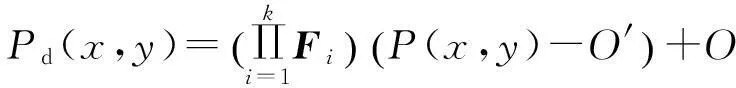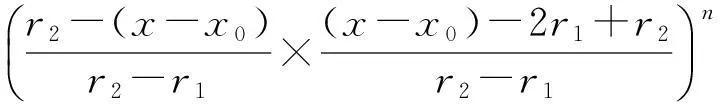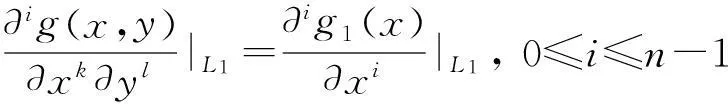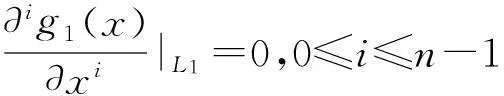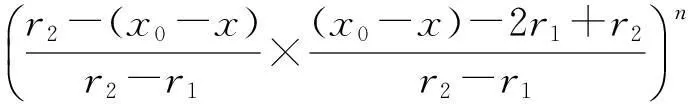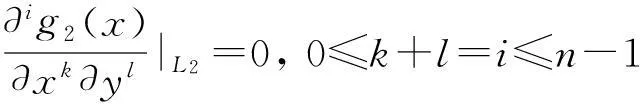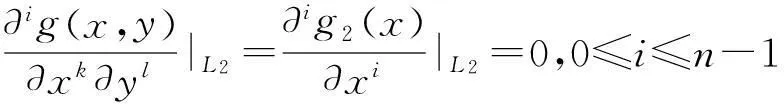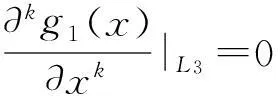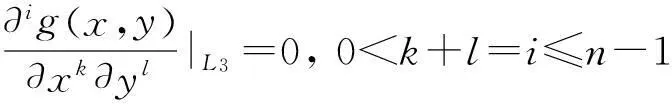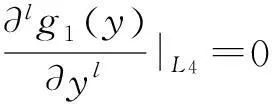矩形域上的参数曲面自由变形算法

张　莉　葛先玉　檀结庆,2

1(合肥工业大学数学学院　合肥　230009)2(合肥工业大学计算机与信息学院　合肥　230009)(lizhang@hfut.edu.cn)

矩形域上的参数曲面自由变形算法

张莉1葛先玉1檀结庆1,2

1(合肥工业大学数学学院合肥230009)2(合肥工业大学计算机与信息学院合肥230009)(lizhang@hfut.edu.cn)

摘要针对参数曲面的自由变形,构造了矩形域上一类带平台的、分片多项式形式的伸缩函数.新的伸缩函数具备了对称性、单点峰值性、线性峰值性和区域峰值性等良好的性质;且具备了简单的多项式形式,易于构造和操控;由此构造的伸缩因子中的各个参数具备明显的几何意义,特别适用于交互设计.将基于伸缩因子构造的变形矩阵作用于待变形的曲面,可以获得诸如凹凸、剪切、伸缩和改变变形中心等各类变形效果,借助于叠加变形可进一步实现丰富多样的复杂变形效果.该文付出了大量的数值实例,展示了各类变形效果以及伸缩函数中各个不同参数对形状的调控.

关键词参数曲面;伸缩因子;自由变形;矩形区域;变形效果

在计算机图形学领域中,物体的变形一直是一个热点问题.从众多的相关研究来看,我们可以将物体变形大致分为基于物理的变形[1]和基于几何的变形.基于物理的变形方法是将物体看作物理实体而非单纯的几何体,根据客观规律对物体进行变形,得到较为逼真的效果.而基于几何的变形方法则是将物体抽象为空间中的几何体,运用CADCAM中的数字几何处理技术对物体形状进行修改、编辑.其数学本质就是对其逐点映射以生成满足特定条件的新的几何形状,与基于物理的变形方法相比较,该类方法计算量小、简单易行、但逼真度欠佳.

有鉴于此,本文针对参数曲面的自由变形,通过构造双变量分片多项式型的伸缩函数,给出了矩形域上一种交互良好,参数几何意义明确,且能在点、线、矩形区域上达到峰值的参数曲面变形算法.这种算法无需依赖新的辅助工具,表达式中的每个参数都具备各自明显的几何属性,可以在交互设计中灵活调用.

1伸缩因子的定义和性质

1.1伸缩函数

首先给出二元伸缩函数的定义.

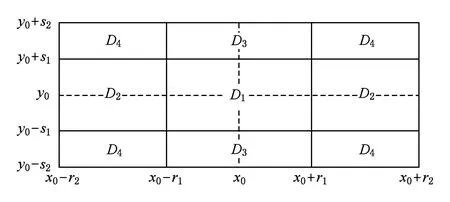
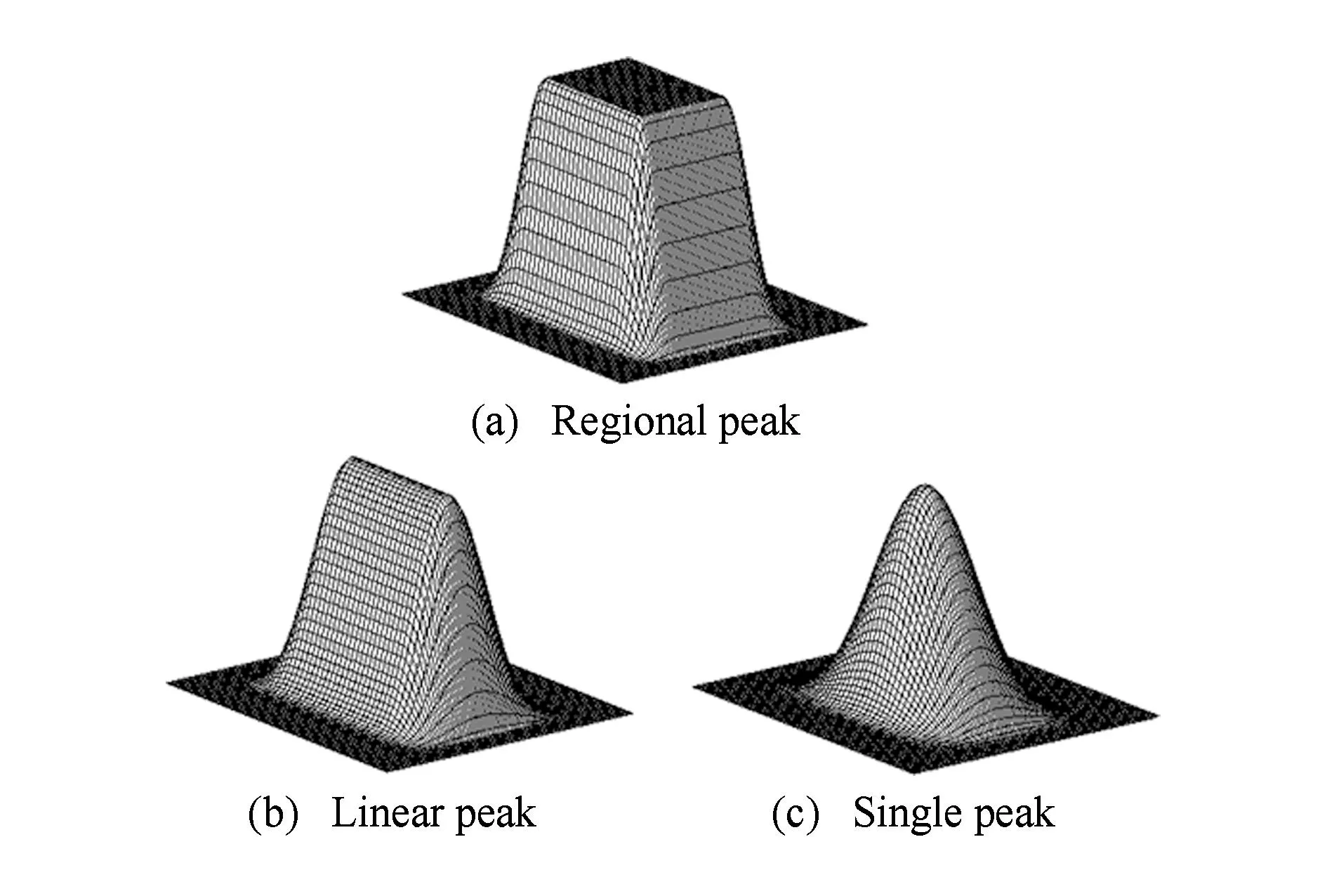
定义1. 设n为正整数,r1,r2,s1,s2均为非负实

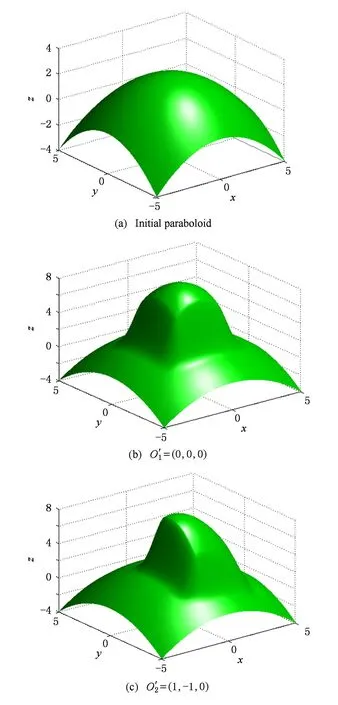
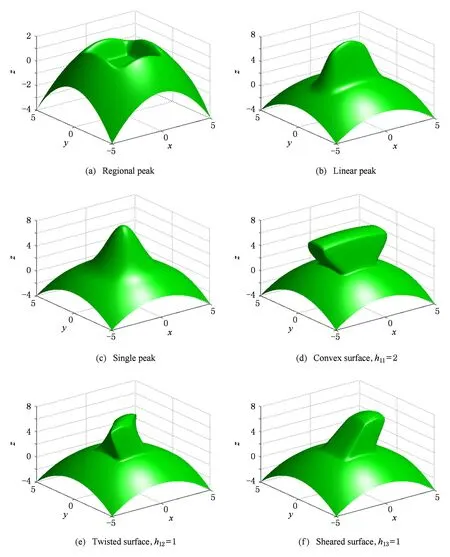
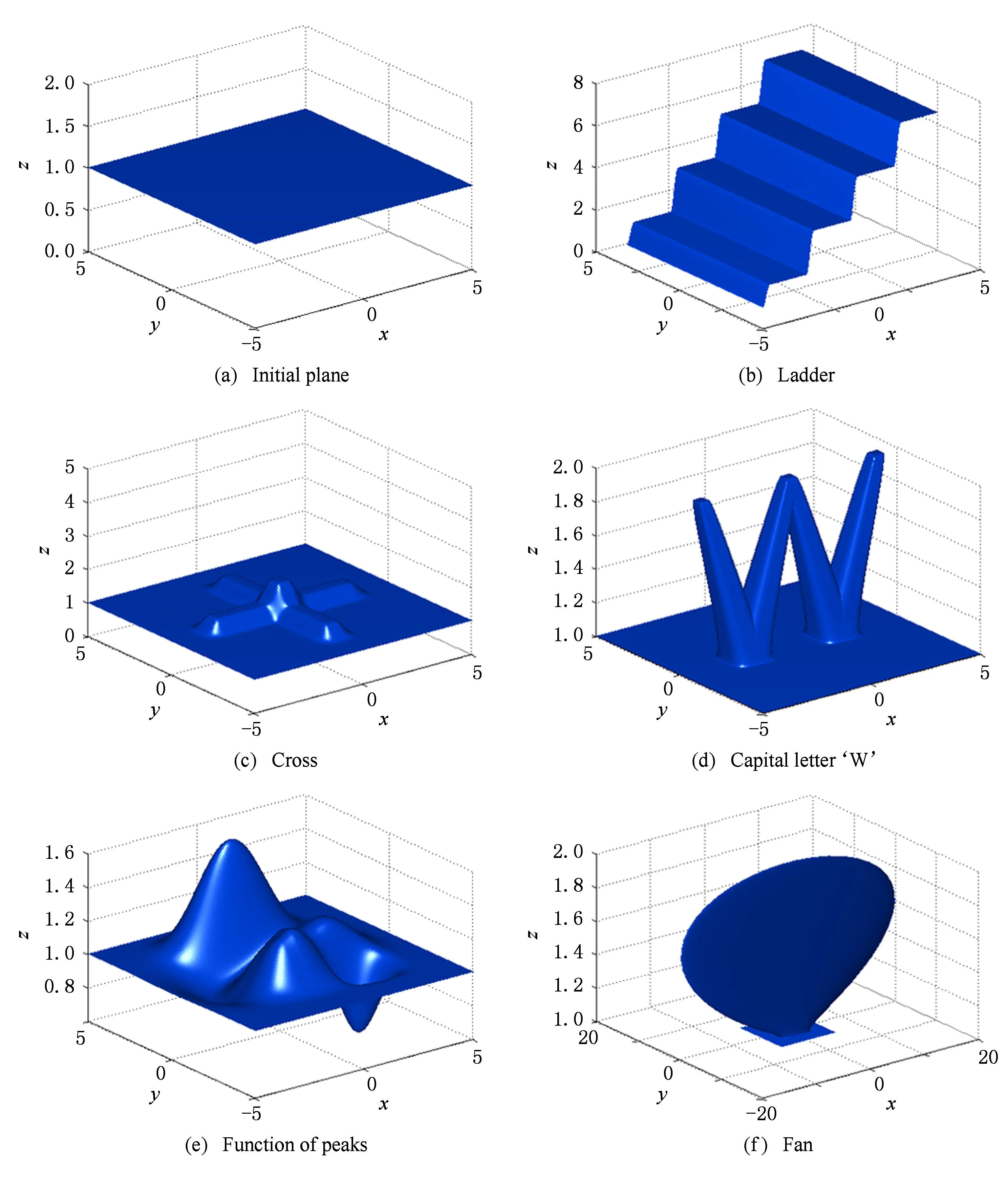
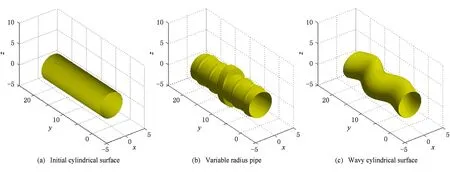
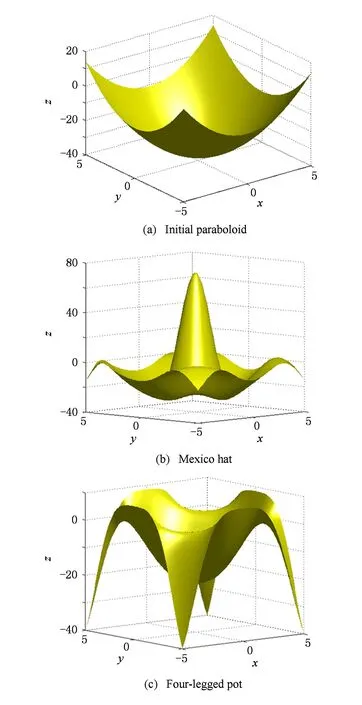
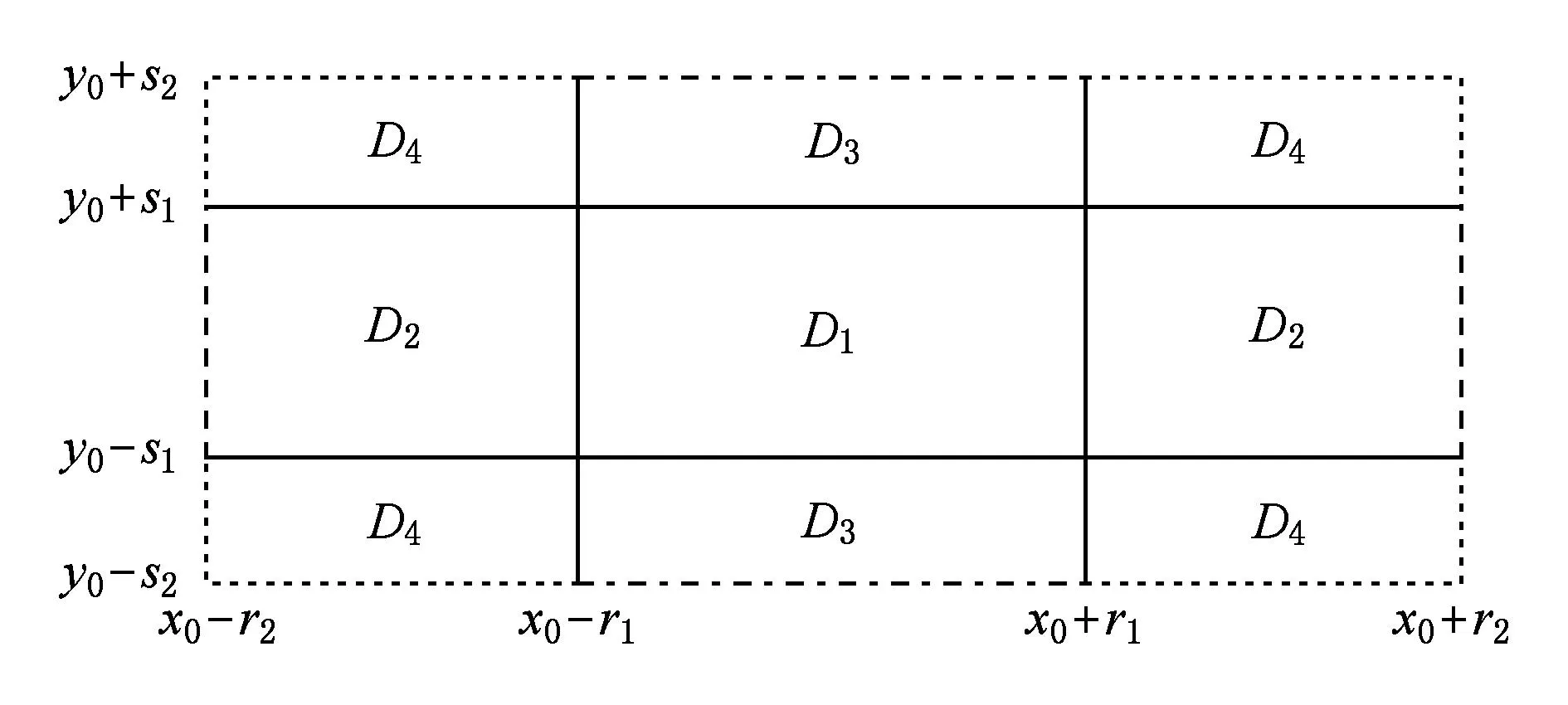
数,其中0≤r1

D1={(x,y)||x-x0|≤r1,|y-y0|≤s1};

D2={(x,y)|r1<|x-x0|≤r2,|y-y0|≤s1};

D3={(x,y)||x-x0|≤r1,s1<|y-y0|≤s2};

D4={(x,y)|r1<|x-x0|≤r2,s1<|y-y0|≤s2};

记D=D1∪D2∪D3∪D4,定义2上伸缩函数如下:

(1)

为表述简便起见,这里的r=|x-x0|,s=|y-y0|.

由定义1可见,二元伸缩函数g(x,y)的支撑区域D共有9个部分,其中D1为峰值区域,区域D2,D3,D4环绕在峰值区域D1的四周,具体分布如图1所示:

Fig. 1　Support area and peak region.图1　支撑区域和峰值区域图

二元伸缩函数g(x,y)具有5个性质:

Fig. 2 　Peak properties of extension function g(x,y).图2　伸缩函数g(x,y)的峰值性

1) 区域峰值.(x,y)∈D1时,g(x,y)取最大值1；(x,y)∉D时,g(x,y)取最小值0,取r1>0,s1>0,g(x,y)在D1上达到峰值,如图2(a)所示.

2) 线型峰值.任取r1和s1中一个为0但不同时为0,这时峰值区域D1退化为线段,g(x,y)在线段上达到峰值,如图2(b)所示.

3) 单点峰值.取r1=0,s1=0,这时峰值区域退化为单点,g(x,y)具有单峰值,如图2(c)所示.

容易证明性质1～3是成立的,性质4，5的证明见附录A.

1.2伸缩因子

定义2. 设h为实数,定义带参数n,h的二元伸缩因子:

(2)

其中，n为光滑参数,h为伸缩参数,D为支撑区域,最值区域为D1.

在式(2)的定义基础上,可以得到伸缩因子具有5个与伸缩函数类似的性质:

1) 区域最值.取r1和s1均大于0,当h≥0时,E(x,y)有最大值1+h,h<0时,E(x,y)有最小值1+h.

2) 线型最值.任取r1和s1中一个为0但不同时为0,E(x,y)在线段上达到最值.

3) 单点最值.r1=0,s1=0,E(x,y)在单点取最值.

4) 支撑区域D的边界∂D处的偏导值：

5) 内部交界处的偏导值：

2空间曲面的变形与控制

2.1变形的数学模型

给定一张空间中的Cu(u≥1)类曲面P(x,y)=f(x,y)(亦可采用参数曲面形式),由定义2,伸缩因子为

Eij(x,y)=1+hij×g(x,y),i,j=1,2,3,

这组伸缩因子具有相同的支撑区域及光滑指数,其中光滑指数n≤u+1.我们称矩阵

则称F=(e1,e2,e3)MN(e1,e2,e3)T为变形矩阵,特殊地,取e1=(1,0,0)T,e2=(0,1,0)T,e3=(0,0,1)T时,F=M.

定义3. 在曲面定义域上选取中心点O′,变形后曲面Pd(x,y)与变形前曲面P(x,y)满足关系:

Pd(x,y)=F×(P(x,y)-O′)+O′,

(3)

P(x,y)-O′=(l1,l2,l3)(c1,c2,c3)T,

则式(3)可以表示为

(4)

由此可以看出定义3中的变形有明确的几何意义:在仿射坐标系[O′,l1,l2,l3]下,对P(x,y)-O′的坐标(c1,c2,c3)T作仿射变换,变换矩阵就是变形矩阵F.

定理1. 待变形曲面为Bézier或NURBS曲面时,变形后曲面为分片Bézier或分片NURBS曲面,即形式上仍为Bézier或NURBS曲面.

证明. 作变换:

(5)

则定义2中伸缩因子可表示为

(6)

若待变形的曲面为K×S次Bézier曲面:

它的控制网格为bi,j(i=0,1,…,K;j=0,1,…,S),在区域D4={(x,y)|r1<|x-x0|≤r2,s1<|y-y0|≤s2},此时,0≤u<1,0≤v<1,作形如式(5)的变换可得:

(7)

(1+hun(2-u)nvn(2-v)n)×

(8)

注意到式(8)中的简单变形,最后2步借助于幂基和Bernstein基的相互转换[20],由于伸缩因子为分片多项式,故而变形后的曲面为分片Bézier曲面.复杂的变形可类似处理.关于NURBS曲面的讨论类似.

2.2叠加变形

通常一次变形不能得到理想的曲面,我们需要对同一个曲面进行多次变形,这里假定为k次,令P0,d(x,y)=P(x,y). 由定义3可知,相邻2次变形Pi,d(x,y),Pi-1,d(x,y),i=1,2,…,k,满足递推关系:

(9)

Fi=(ei1,ei2,ei3)MiNi(ei1,ei2,ei3)T,

其中ei1,ei2,ei3和Mi分别为第i变形的主方向及伸缩矩阵,这里:

特别地,当变形中心均取同一点O′时,经过k次变形后曲面Pd(x,y)与初始曲面P(x,y)满足关系:

(10)

2.3变形与控制

在变形过程中,通过改变控制变形中心、峰值区域、光滑度、主方向等各个参数,可以对待变形的初始曲面形状进行灵活的控制,以得到理想的曲面.

1) 要控制曲面的变形中心,只需改变O′.

2) 要控制曲面的峰值区域,可通过改变r1,s1.另外,r2和s2控制曲面变形的支撑区域.

3) 要控制变形曲面在支撑区域边界的光滑度,可通过改变n的大小,n越大,变形后曲面与待变曲面越靠近.

4) 要控制曲面的变形主方向,只需改变e1,e2,e3.

5) 改变hi i的符号,可以控制变形曲面沿主方向ei的正向或负向变形,改变|hi i|的大小,控制曲面沿ei变形的幅度,其中i=1,2,3.改变h12,h13的符号,可以控制曲面沿e1的正向或负向剪切,改变|h12|, |h13|的大小,可以得到不同的剪切效果,值越大,剪切效果越明显.类似地,可以通过h21,h23控制曲面沿e2的剪切效果,通过h31,h32控制曲面沿e3的剪切效果.在实际应用中,通常同时改变多个参数,以达到理想的变形效果.

3数值实例

例1. 图3、图4以抛物面z=(2-x2-y2)8+2为例,取光滑指数n=4,依次展示了改变控制参数引起的实际效果.为了方便起见,在本例中取主方向为坐标轴方向.图3(a)为原始抛物面.取变形中心1=(0,0,0),参数r1=1.5,s1=1.5,r2=3.5,s2=3.5来确定变形的峰值区域及支撑区域,取参数hi j(i,j=1,2,3)中h33=2.5,其余为0,获得图3(b)所示变形效果,原始抛物面在支撑区域内沿主方向e3(本例中即为z轴)正向伸展变形.上述参数不变,仅改变变形中心为2=(1,-1,0),所得伸展变形效果见图3(c).取变形中心O′=(0,0,0),通过对参数r1,s1的调控可以让初始抛物面达到不同类型峰值区域的效果,如图4(a)(b)(c)所示,依次取得区域峰值、线型峰值、单点峰值.给定相同的支撑区域和峰值区域,取h11=2,得到曲面沿x轴凸出的效果图(如图4(d)所示),分别取h12,h13=1,得到如图4(e)和图4(f)两种沿x轴方向不同的剪切效果.图4中各个子图具体参数赋值情况如表1所示.

Fig. 3　Effects of changing deformation center O′.图3　改变变形中心O′的效果

Iconr1s1r2s2hij(i,j=1,2,3)Fig.4(a)1.51.533h33=-1,otherhij=0Fig.4(b)1.5042h33=2.5,otherhij=0Fig.4(c)0044h33=2.5,otherhij=0Fig.4(d)1122h33=2,h11=2,otherhij=0Fig.4(e)1122h33=2,h12=1,otherhij=0Fig.4(f)1122h33=2,h13=1,otherhij=0

Fig. 4　Deformation effects after changing different parameters at the deformation center O′=(0,0,0)(see Table 1).图4　O′=(0,0,0)处不同参数(如表1所示)变化得到的曲面变形效果

例2. 以平面z=1(如图5(a)所示)为例,展示了复杂变形效果.图5(b)是在原平面基础上沿着z轴连续4次上凸变形得到的.图5(c)通过2次变形得到十字架模型.在图5(d)中,对平面进行4次叠加变形,用h33控制每次伸缩的长度,h13控制其摇摆的角度.图5(e)则展示了对平面连续5次伸缩得到类似于peaks函数曲面效果.在图5(f)中我们同时控制h33,h11,使得变形沿z轴上凸且沿x轴正负方向拉伸,得到类似扇子的形状.上述各图表明,通过调控各参数,变形操作可以在点、线和区域达到峰值,将变形复合和叠加,可以灵活地控制和调整变形曲面的形状,得到丰富多彩的效果.

Fig. 5　Complex deformation effects of the plane.图5　平面上复杂变形效果

Fig. 6　Complex deformation effects of cylindrical surface.图6　圆柱面的复杂变形效果

Fig. 7　Complex deformation effects of paraboloid.图7　抛物面的复杂变形效果

4结论

本文针对参数曲面的自由变形,构造了分片的双变量多项式类型的伸缩函数,考察了它在变形区域的边界及内部各个矩形区域交界处的偏导值,给出了一种交互性良好、几何意义明确的新型参数曲面变形算法.该算法无需依赖任何辅助工具,不仅可以在单点处达到峰值,也可以在线、矩形区域上达到峰值,且表达式中的每个参数都具备各自明显的几何属性.对于任意参数形式的曲面,我们可以通过调控各个变形参数得到期望的变形效果.

本文所给出的参数曲面自由变形方法,本质上是通过建立二元的伸缩函数,借助于伸缩因子和变形矩阵来实现参数曲面的自由变形,尽管具有交互简单、几何意义直观等特点,但变形效果也受伸缩函数的约束,无法实现现有自由变形算法中一些效果,如基于体的变形方法中可实现的任意拓扑的变形、多分辨率变形[10],基于曲面的变形方法中可实现的基于细分曲面的多分辨率变形[21]、基于扫掠曲面的多层次的联动变形[22]等.

参考文献

[1]Che Yinghui, Liang Xiaohui, Zhao Qinping. A physically-based detail-preserving algorithm for real-time deformation[J]. Journal of Computer Research and Development, 2008, 45(3): 503-509 (in Chinese)(车英慧, 梁晓辉, 赵沁平. 一种基于物理的实时细节保持变形算法[J]. 计算机研究与发展, 2008, 45(3): 503-509)

[2]Xu Gang, Wang Guozhao, Chen Xiaodiao. Free form deformation and its application[J]. Journal of Computer Research and Development, 2010, 47(2): 344-352 (in Chinese)(徐岗, 汪国昭, 陈小雕. 自由变形技术及其应用[J]. 计算机研究与发展, 2010, 47(2): 344-352)

[3]Barr A H. Global and local of deformation of solid primitive[J]. Computer Graphics, 1984, 18(3): 21-30

[4]Ugüdükbay U, ōzgüc B. Free-form solid modeling using deformation[J]. Computer & Graphics, 1990, 14(34): 491-500

[5]Sederberg T W, Parry R. Free-form deformations of solid geometric models[J]. Computer Graphics, 1986, 20(4): 151-160

[6]Griessmair J, Purgathofer W. Deformation of solids with trivariate B-splines[C]Proc of Eurographics’89. New York: Wiley, 1989: 137-148

[7]MacCracken R, Joy K I. Free-form deformations with lattices of arbitrary topology[J]. Computer Graphics, 1996, 30(4): 181-188

[8]Huang Haiyun, Qi Feihu, Yao Zhihong. A leg motion modeling method based on NURBS free-form deformation[J]. Journal of Computer Research and Development, 2000, 37(6): 697-702 (in Chinese)(黄海赟, 戚飞虎, 姚志洪. 基于NURBS自由变形的腿部运动建模方法[J]. 计算机研究与发展, 2000, 37(6): 697-702)

[9]Song Wenhao, Yang Xunnian. Free-form deformation with weighted T-spline[J]. The Visual Computer, 2005, 21(3): 139-151

[10]Xu Gang, Wang Guozhao, Chen Xiaodiao. Free-form deformation with rational DMS-spline volumes[J]. Journal of Computer Science and Technology, 2008, 23(5): 862-873

[11]Lazarus F, Coquillart S, Jancene P. Axial deformations: An intuitive deformation technique[J]. Computer Aided Design, 1994, 26(8): 607-613

[12]Feng Jieqing, Ma Lizhuang, Peng Qunsheng. A new free-form deformation through the control of parametric surfaces[J]. Computer & Graphics, 1996, 20(4): 531-539

[13]Feng Jieqing, Ma Lizhuang, Peng Qunsheng. Free-form deformation through embedding objects into the parametric domain of surface[J]. Journal of Computer-Aided Design & Computer Graphics, 1998, 10(3): 208-215 (in Chinese)(冯结青, 马利庄, 彭群生. 嵌入参数空间的曲面控制自由变形方法[J]. 计算机辅助设计与图形学学报, 1998, 10(3): 208-215)

[14]Zhao Yong, Xiao Chunxia, Shi Feng, et al. Rigid mesh deformation with detail preserving[J]. Journal of Computer Research and Development, 2010, 47(1): 1-7(in Chinese)(赵勇, 肖春霞, 石峰, 等. 保细节的网格刚性变形算法[J]. 计算机研究与发展, 2010, 47(1): 1-7)

[15]Xu Gang, Hui Kinchuen, Ge Wenbing, et al. Direct manipulation of free-form deformation using curve-pairs[J]. Computer-Aided Design, 2013, 45(3): 605-614

[16]Wang Xiaoping, Ye Zhenglin, Meng Yaqin, et al. Free-form deformation based on extension factor for parametric curve[J]. Journal of Computer-Aided Design & Computer Graphics, 2002, 14(1): 66-69 (in Chinese)(王小平, 叶正麟, 孙雅琴, 等. 基于伸缩因子的参数曲线自由变形[J]. 计算机辅助设计与图形学学报, 2002, 14(1): 66-69)

[17]Wang Xiaoping, Ye Zhenglin, Meng Yaqin, et al. Space deformation of parametric surface based on extension function[J]. International Journal of CADCAM, 2002, 1(1): 23-32

[18]Liu Zhi, Wu Hongyi, Zhang Li, et al. Method of polynomial factor for free-form deformation of parametric curves and surfaces[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(3): 412-418 (in Chinese)(刘植, 邬弘毅, 张莉, 等. 参数曲线曲面自由变形的多项式因子方法[J]. 计算机辅助设计与图形学学报, 2009, 21(3): 412-418)

[19]Lu Youtai, Zhou Laishui, Wang Zhiguo, et al. Free-form deformation based on power extension factor for parametric curves[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 43(6): 793-798 (in Chinese)(陆友太, 周来水, 王志国, 等. 基于乘幂伸缩因子的参数曲线自由变形[J]. 南京航空航天大学学报, 2012, 43(6): 793-798) [20]Wang Guojin, Wang Guozhao, Zheng Jianmin. Computer Aided Geometric Design[M]. Beijing: China Higher Education Press, 2001: 14-15 (in Chinese)(王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M]. 北京: 高等教育出版社, 2001: 14-15)

[21]Feng Jieqing, Shao Jin, Jin Xiaogang, et al. Multiresolution free-form deformation with subdivision surface of arbitrary topology[J]. The Visual Computer, 2006, 22(1): 28-42

[22]Yoon S H, Kim M S. Sweep-based free form deformation[J]. Computer GraphicsForum, 2006, 25(3): 487-496

Zhang Li, born in 1976. PhD and professor in Hefei University of Technology. Member of China Computer Federation. Her main research interests include computer-aided geometric design & computer graphics.

Ge Xianyu, born in 1991.Master candidate in Hefei University of Technology. His main research interests include computer-aided geometric design & computer graphics (shuxuegxy@126.com).

Tan Jieqing, born in 1962. Professor and PhD supervisor in Hefei University of Technology. His main research interests include non-linear numerical approximation theory, computer-aided geometric design and computer graphics. (jieqingtan@hfut.edu.cn).

附录A.

正文定义1中二元伸缩函数g(x,y)性质4和性质5的证明.

证明.

1) 性质4证明.由正文图1可知,支撑区域D的边界是由x=x0±r2,y=y0±s2, 4条线段围成,按照二元伸缩函数在各个区域上的表达式,将D的边界如图A1所示分成3类:虚线段、点划线段和点线段.

Fig. A1　Classified support area and peak region.图A1　分类后的支撑区域和峰值区域图

(1) 求解虚线段处的偏导值

二元伸缩函数g(x,y)在x=x0±r2作为区域D2边界处的偏导值,即图A1中虚线段.

①x=x0+r2时,记:

L1={(x,y)|x=x0+r2,y0-s1≤y≤y0+s1},

由二元伸缩函数的定义知,(x,y)∈L1时,

g(x,y)=g1(x)=

g(x,y)实际上是关于x的一元函数,不妨记为g1(x),它关于y的偏导数值为0.从而当l≠0时,

0≤k+l=i≤n-1,

l=0时,相当于对函数g1(x)求解在x=x0+r2处直到n-1阶的导数值,即:

(x-x0-2r1+r2)n-k,

其中:

c=Cki(-1)i-kn(n-1)…

(n-i+k+1)n(n-1)…(n-k+1),

由于0≤i≤n-1,且n-i+k≥1,代入边界信息,有:

②x=x0-r2时,记:

L2={(x,y)|x=x0-r2,y0-s1≤y≤y0+s1},

由二元伸缩函数的定义知,当(x,y)∈L2时,

g(x,y)=g2(x)=

g(x,y)实际上是关于x的一元函数,不妨记为g2(x),它关于y的偏导数值为零,即当l≠0时,

l=0时,求g2(x)在x=x0-r2处直到n-1阶的导数值,类似于g1(x)的证明,我们有:

(2) 求解点划线段处的偏导值.

从式(1)可以看出,g(x,y)在区域D2是x的单变量函数,而在D3上恰好是y的单变量函数,轮换变量x和y,上述对于D2边界处偏导值的证明同样适用于D3的边界,从而可证明g(x,y)在点划线段上偏导值为0.

(3) 求解点线段处的偏导值

图A1中点线段为区域D4的边界.由二元伸缩函数的对称性,我们仅需考虑右上角的一部分,记:

L3={(x,y)|x=x0+r2,y0+s1≤y≤y0+s2};

L4={(x,y)|x0+r1≤x≤x0+r2,y=y0+s2};

当(x,y)∈L3,

g(x,y)=g1(x)×g1(y)=

g(x,y)为变量可分离的二元伸缩函数,因此有:

类似本证明步骤①②中关于x或者关于y的偏导值求解过程,可得:

从而:

这样整个边界∂D的偏导值即证.

2) 同理可以证明性质5.

证毕.

Free Form Deformation Method of Parametric Surfaces on Rectangular Region

Zhang Li1, Ge Xianyu1, and Tan Jieqing1,2

1(SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009)2(SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei230009)

AbstractAccording to free form deformation of parametric surfaces, a new method based on extension function is proposed. It is made by piecewise polynomials and defined on rectangular region. Based on these, the new extension factor we constructed not only possesses perfect properties such as symmetry, single peak, linear peak and region peak, but also holds some parameters which have obvious geometric meanings. In real applications, the extension factor is very suitable for interactive design due to these properties and extraordinary parameters. Furthermore, the new extension factor is easy to construct and convenient to control because of its simple polynomial forms. Applying the deformation matrix constructed by the new extension factor to the original surfaces’ equations, plentiful deformation surfaces can be achieved. Deformation effects such as shearing, concave & convex, expand & contract and changing of deformation center can be obtained. With the help of superimposing, more complex deformation effects can be realized. Lots of numerical experiments are given at the end of paper which illustrate different kinds of deformation effects and plentiful adjusting effects of different parameters.

Key wordsparametric surface; extension factor; free form deformation; rectangular region; deformation effects

收稿日期：2014-11-28；修回日期：2015-08-11

基金项目：国家自然科学基金-广东联合基金重点项目(U1135003)；国家自然科学基金项目(61472466,61100126)；安徽省自然科学基金项目(1508085QF116)；中央高校基本科研业务费专项资金项目(JZ2015HGXJ0175)；中国博士后科学基金项目(2015M571926)

中图法分类号TP391.41

This work was supported by the National Natural Science Foundation of China-Guangdong Joint Foundation Key Project (U1135003), the National Natural Science Foundation of China (61472466,61100126), the Natural Science Fundation of Anhui Province of China (1508085QF116), and the Fundamental Research Funds for the Central Universities (JZ2015HGXJ0175), and the China Postdoctoral Science Foundation (2015M571926).