基于概率和代表点的数据流动态聚类算法

毕安琪　董爱美,2　王士同

1(江南大学数字媒体学院　江苏无锡　214122)2(齐鲁工业大学信息学院　济南　250353)(angela.sue.bi@gmail.com)

基于概率和代表点的数据流动态聚类算法

毕安琪1董爱美1,2王士同1

1(江南大学数字媒体学院江苏无锡214122)2(齐鲁工业大学信息学院济南250353)(angela.sue.bi@gmail.com)

摘要为了解决数据流动态聚类问题，提出了一种概率化的基于代表点聚类算法.首先，基于概率框架给出了AP(affinity propagation)聚类算法和EEM(enhanced α-expansion move)聚类算法的联合目标函数，提出了概率化的基于代表点聚类算法;其次，根据样本与其代表点之间的概率，提出了基于概率的漂移动态α-expansion数据流聚类算法.该算法使得新数据的代表点尽可能贴近原始数据的代表点，从而提高聚类性能;另一方面，考虑到原始数据与新数据的相似性，该算法能够处理2种漂移过程中的动态聚类问题：1)新数据与原始数据分享部分数据，其余数据与原始数据相似；2)没有相同的数据，新数据与原始数据有相似关系.在人工合成数据集D31,Birch3以及真实数据集Forest Covertpye,KDD CUP99的实验结果均显示出了所提之算法能够处理数据流聚类问题，并保证聚类性能稳定.

关键词数据流;能量函数;概率;优化算法;动态聚类

在机器学习领域，聚类算法受到了研究者们广泛的重视和研究.作为一种无监督学习方法，基于不同的聚类特征和理论，研究者们发展出了各具特色的不同聚类算法，例如基于类中心的聚类分析方法、基于谱理论的聚类分析方法以及基于密度的聚类分析方法等[1-8].随着信息技术以及社交网络的蓬勃发展，人们在现实生活中经常选择一个已存在的实例作为数据簇的类中心(如一位领导或一个代表).AP(affinity propagation)聚类算法作为一种典型的基于实例点聚类的方法，于近年来受到广泛的关注和使用.2007年，Frey等人[9]将这些实例类中心称为代表点(exemplar)，并在文献[9-10]中证明了此类基于代表点的聚类问题可以看作是Markov随机场(Markov random field, MRF)的能量函数寻优问题.因此，可以用MRF能量函数的优化算法求解这类聚类问题，MRF的优化算法主要有2种方法：1)基于信息传递的LBP(loopy belief propagation)算法[10]；2)基于Graph Cuts的优化算法，例如α-expansion[11-12].众所周知，经典的AP聚类算法即是使用LBP算法优化目标函数进行求解的.然而，2001年文献[12]通过实验证明α-expansion优化算法较之LBP算法在获取最终优化结果上更显优势.因此,2013年，Zheng等人[13]证明基于代表点的聚类算法的目标函数可以用α-expansion优化算法进行求解，从而提出了一种新的基于代表点的聚类算法EEM(enhancedα-expansion move)，并通过实验证明了EEM算法具备更加高效的聚类性能.

近年来，针对数据流(data stream)的机器学习方法成为研究热点，基于数据流的动态聚类算法也是重点之一.数据流是指数据特征随着时间的推移而发生变化的一种特殊数据，例如股票行情分析、网络流量分析、网络异常检测、传感器检测是机器学习领域出现的一种新的数据模型.现阶段针对数据流的研究主要集中在动态聚类[13-21]、突变检测[22-23]等方面，并且都取得了标志性成果.鉴于数据流动态聚类算法的良好应用前景，本文将主要关注动态聚类算法，值得指出的是，本文所研究的问题其前提是数据流数据特征不发生突变，同时新流入的数据应该与原始数据保持一定的相似性，如图1所示.而新数据与原始数据的相似性关系可以分为2种情况：1)部分新数据与原始数据完全相同，其余数据与原始数据相似；2)新数据与原始数据没有相同的数据，仅保持相似关系.

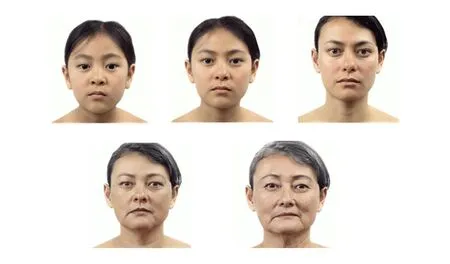
Fig. 1　Data stream without sudden change.图1　数据流数据

根据上述数据流数据的特征，经研究可知目前的AP聚类方法及其改进方法[9,11-12]尚不能解决此类动态聚类问题.根据数据流数据特征随时间变化这个特征，数据流动态聚类算法需要能够追踪原本数据的聚类结果，并结合这类已知信息与新获取数据提高当前的聚类性能.因此，数据流动态聚类算法应该至少能够解决2个问题：1)针对新数据的聚类性能必须不低于以往数据的聚类性能；2)在聚类过程中，由于聚类个数很难事先设定，因此数据流聚类算法必须能够自动识别类的个数.

在静态数据聚类算法的基础上，数据流的动态聚类算法近年来已经取得了一些具有代表性的成果.Guha等人[14]扩展了K-means聚类算法使之适用于数据流聚类，之后O’ Calloghan等人[15]提出了STREAM算法，采用分级聚类的技术提高了算法的聚类性能.同时，Aggarwal等人[16-17]提出了CluStream算法以及HPStream算法，提出了用微簇来保存聚类的概要数据，其扩展了BIRCH算法中聚类特征的概念，这2种算法是现在数据流聚类算法中的经典算法.Cao等人[18]提出了一种基于密度的聚类算法DenStream，同样采用了CluStream中的在线和离线2阶段的思想.然而，这类算法一般通过衰减因子来控制原始数据与新数据之间的相似性关系，当原始数据与新数据分享部分数据时，这类算法的聚类性能并不稳定.

对于现有的AP算法而言，其在处理数据流聚类问题时，通常的做法是通过对样本集的二次计算获取针对当前数据的聚类结果，使其不适用于动态聚类的情况，并且不能有效检测出数据流的变化.为解决这一问题，使得能量函数的优化算法能够适应数据流的动态聚类.本文在AP聚类算法和EEM聚类算法的基础上，提出了一种新的基于概率的漂移动态α-expansion聚类算法(probability drifting dynamicα-expansion clustering algorithm， PDDE).该算法基于MRF能量函数寻优问题，首先基于概率论给出AP聚类算法和EEM聚类算法的联合目标函数，之后充分利用原样本集与新数据的相似性，通过样本的概率信息并借助原样本数据的聚类结果，在使得新数据的代表点与原数据的代表点尽可能相似的目标下，最终提高对新数据的聚类性能，解决数据流动态聚类所面对的问题1.对于问题2，由于本文采用了基于代表点聚类算法作为基础算法，而该类聚类算法本身即能够完成自动聚类而无需预先设定聚类个数，因此问题2被自然地解决了.另一方面，由于引入概率框架，当原始数据与新数据分享部分数据时，PDDE聚类算法仍然可以进行数据流动态聚类，即该聚类算法将原始数据与新数据的2种相似性关系统一.

1基于代表点聚类算法及相关扩展

基于代表点的聚类算法由于已经解决了数据流动态聚类所面临的第2个问题，使得它在解决这类特殊的聚类问题时拥有一定的优势.在基于代表点的聚类算法中，具有代表性的研究成果之一就是文献[9]证明了该类聚类算法目标函数等价于MRF的能量函数寻优问题，并将这些实例类中心称为代表点.基于这一重要结论，如引言所说，根据MRF能量函数的不同的优化方法，这类聚类算法主要分成2种：1)使用LBP(loopy belief propagation)算法[11]优化，例如AP算法；2)使用Graph Cuts算法优化，例如EEM算法.本节将以AP算法和EEM算法为例，在1.1节和1.2节对这2类算法作简要的介绍与分析.之后利用概率框架统一这2种算法，进而引导出新的基于此框架的数据流动态聚类算法.

1.1AP聚类算法

AP聚类算法的目标函数如下：

(1)

其中，xp表示样本点集合中第p个样本点；N是样本集中样本点的个数，c是待求的代表点集合；cp即为样本点集合中第p个样本点xp的代表点；d(xp,xcp)表示样本点xp与其代表点xcp之间的距离，一般使用欧氏距离.AP聚类算法使用LBP优化算法求解该目标函数，并定义了2个变量r(i,k)表示候选代表点xk作为样本点xi的代表点的合适程度，而a(i,k)表示样本点xi与候选代表点xk的适合程度.具体地，两者迭代公式为

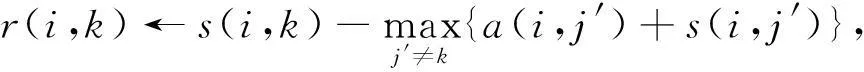
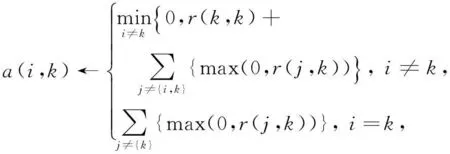
(2)

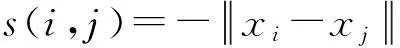
(3)

其中，la∈[0,1]，默认为0.5，称为阻尼系数(damping factor).阻尼系数还有一个重要的作用是改进算法的收敛性：当算法发生震荡不能收敛时，增大la可以消除震荡.

AP算法完全突出了类中心需要预设的限定条件且其聚类结果十分稳定，受到了近年来的广泛关注和研究.但由于AP算法采用了LBP策略，该优化策略并不能保证其收敛性，文献[9]使用阻尼技术来解决这个问题，然而，阻尼系数的选择是一个非常精细的工作，不适合的阻尼系数通常会导致算法不收敛.另外，由于AP算法仅考虑某一时刻的数据，并不能借助于基于原始数据的相关结论来提高当前数据的聚类性能.因此，这些缺陷使得这种经典的AP聚类算法不能用来解决数据流动态聚类问题.

1.2EEM聚类算法

对于MRF的能量函数寻优问题，2003年，文献[11]已经通过实验证明以α-expansion为代表的Graph Cuts优化算法比LBP更优，但是α-expansion优化算法仅能使用于基于样本两两间关系(pairwise submodular)的能量函数优化问题.因此，2013年，文献[13]证明α-expansion优化算法也可以用来解决基于代表点的聚类算法的目标函数寻优问题，并基于此提出了一种改进的算法称为EEM聚类算法.

EEM聚类算法的目标函数为

(4)

与AP聚类算法类似，目标函数中xp表示样本点集合中第p个样本点，c是待求的样本点集合，θp,q(cp,cq)是使得代表点集合c有效的约束项，文献[13]已证明：

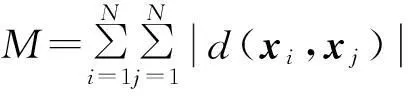
对于∀p,q,cp,cq,α∈{1,2,…,N}，有

θp,q(cp,cq)+θp,q(α,α)≤θp,q(cp,α)+θp,q(α,cq)

(5)

成立.

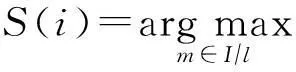
EEM聚类算法是基于代表点聚类算法的最新研究成果，由于使用了不同于AP算法的优化算法，实验证明EEM算法比AP算法更高效、更稳定.虽然文献[2]所提出的EEM算法并不能直接解决数据流的动态聚类问题，但是其提供了一个新的解决该类问题的框架，基于此框架本文第3节提出了一种新的动态数据流聚类算法，考虑到EEM算法在传统聚类问题中体现出的高性能，该算法在解决动态数据聚类问题时具有不错的应用前景.

1.3概率框架下的基于代表点聚类算法

分析AP算法和EEM算法，发现两者目标函数之间的相似性.2类算法均将聚类问题看作MRF能量函数的寻优问题，本节将利用概率的信息表征特征，基于最大后验概率(maximum a posteriori, MAP)原理，给出一个AP算法和EEM算法的联合目标函数.

给定数据样本集合X={x1,x2,…,xN}∈N×D(N为样本总量、D为样本维数)，E={E(x1),E(x2),…,E(xN)}为样本选择的代表点集合，有效的代表点集合E必须满足：如果样本集中有其他样本选择xi作为代表点，则样本xi必须选择其本身为代表点，即如果存在xj，其E(xj)=i，则必须E(xi)=i，即∀i∈{1,2,…,N},E(E(xi))=E(xi).

1.3.1相关概念

高斯混合模型(Gaussian mixture model, GMM)能够平滑地近似任意形状的概率密度，根据GMM的概率密度函数，本文定义代表点集合的先验概率以及样本点和代表点的概率关系如下，其中σ与高斯核中的参数一致：

定义1. 当前代表点集合E的先验概率为

(6)

其中:

(7)

且M是一个足够大的常数.

定义2. 样本点xi与当前代表点集合E中的E(xi)的概率关系如下：

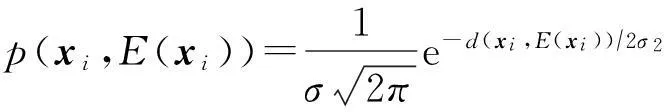
(8)

其中d(xi,E(xi))表示样本xi与代表点E(xi)之间的欧氏距离，可以作为相似性的一种度量方法.

1.3.2基于概率的代表点聚类算法描述

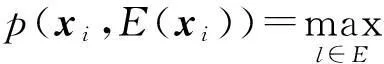
(9)

定义1,2中的常数项不影响目标函数的求解，因此目标函数式(9)可以表示为

(10)

当其中的参数取不同数值时，该目标函数将等价于AP算法和EEM算法的目标函数：

1) 当σ=1时，分析该式与EEM算法的目标函数式(4)，发现式(10)等价于MRF里的最小能量函数的寻优问题，并可以用改进的α-expansion算法进行优化，此时EEM聚类算法是该目标函数的一种特例.

2) 当M=∞且σ=1时，式(10)等价于式(1)，同样可以看作是MRF的能量函数寻优问题，若使用LBP优化算法求解，即为AP聚类算法，因此AP聚类算法是该目标函数的另一种特例.

由以上2点可知，AP算法和EEM算法都要求σ=1，因此本文仅考虑σ=1的情况，而σ取其他值的情况不在本文的讨论范围内.在本节中利用目标函数式(10)将2种典型的基于代表点的算法——AP聚类算法和EEM聚类算法——统一起来，使得基于代表点的算法应用得更加广泛，方便在数据流动态聚类中使用这种思想.另外，由于定义1,2直接给出了样本点xi选择当前代表点集合中代表点E(xi)的概率以及代表点集合E的先验概率，因而在数据特征不发生突变的情况下能够直接度量样本点及其代表点的概率关系，并且自然地运用于数据流的动态聚类问题中.

2基于概率的漂移动态α-expansion聚类算法

2.1基本概念

定义3. 数据流.令k表示任意时间点，Xk表示该时间达到的样本集合，因此，数据流可以表示为若干样本集合DS={X1,X2,…,Xk,…}.

定义4. 数据漂移.数据漂移描述的是在数据流DS={X1,X2,…,Xk,…}上变化的样本集合.当2个样本集合A和B，数据漂移算法依次处理样本集合，在时刻k样本集合A是稳定的，经过时间Δt后，样本集合为B，即在时间Δt内样本集合由A漂移为B.从数据漂移速度上来说，一般将数据漂移分为突变与不发生突变2种类型，本文主要研究的是不发生突变数据漂移聚类问题.

2.2算法框架

本文研究的动态数据聚类算法是在数据漂移且特征不发生突变的情况下对数据流进行聚类分析.为方便下文的研究，设原始数据聚类产生的代表点集合为E0，x0表示漂移的样本点，N0表示漂移的样本数，xi表示当前需处理的样本点，N表示当前样本总数.由于数据流数据的特性以及本文研究的数据环境，在动态数据流算法的构造过程中主要考虑到2点：1)与目标函数式(10)的构造目的一致，在数据流动态聚类中，当前样本从已确定的代表点集合中选择概率最大的代表点，如图2(a)所示，所有样本根据自身与代表点集合中代表点的概率关系选择其中的E(a)，E(b)，E(c)为代表点；2)由于不同时间点样本间的相似性，动态聚类算法所产生的代表点应该与原始数据产生的代表点具有高度的相似性，如图2所示，图2(b)为原始数据的聚类结果，图2(a)为某一时刻数据聚类结果，图2(a)与图2(b)具有相似性，即图2(a)(b)中的代表点具有相似性.

Fig. 2　Dynamic clustering for data stream.图2　数据流动态聚类过程

因此，PDDE聚类算法的目标函数为

(11)

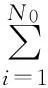
在原始样本点高效聚类的前提下，PDDE聚类算法的构造不考虑数据量很大的原始样本集，仅借鉴了原始样本的代表点信息，因此相比其他的数据流聚类算法，PDDE算法能够更快地完成算法优化.根据之前对基于代表点的聚类算法与MRF能量函数之间关系的研究，PDDE聚类算法的目标函数式(11)也可以看作是MRF能量函数的优化问题.

文献[13]中已经证明EEM的目标函数，即式(4)可以用α-expansion算法进行优化，以α-expansion算法为代表的Graph Cut优化算法，在求解MRF能量函数问题时已被证明优于LBP优化算法.基于文献[13]的结论，可以证明PDDE算法的目标函数式(11)也可以使用α-expansion算法进行优化，证明过程如下：

证明. 不考虑公式中常数项的影响，式(11)可以变为

(12)

ηi,j(E(xi),E(xj))+ηi,j(α,α)≤

ηi,j(E(xi),α)+ηi,j(α,E(xj))

(13)

成立.同时，文献[25]证明，当式(13)成立时，形如目标函数式(12)的能量函数可以用α-expansion算法优化.

证毕.

根据一般的α-expansion优化算法，每次迭代时，根据α的不同，样本点有2种选择:1)代表点不变；2)代表点变为α.然而，若按这种寻优方式，将会使得算法的时间复杂度较大，因此本文将使用一种改进的α-expansion算法来优化目标函数式(11)，将在2.3节详细讨论.

2.3算法优化

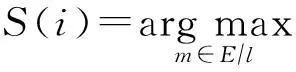
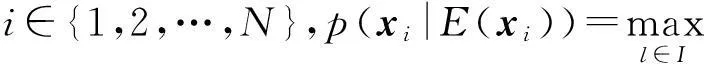
具体的优化过程，根据当前样本点的种类将分为2种情况.由于常数项不影响算法的性能，因此若无特殊说明，本文下面的优化算法过程中涉及能量耗损都已经忽略了常数项的影响.

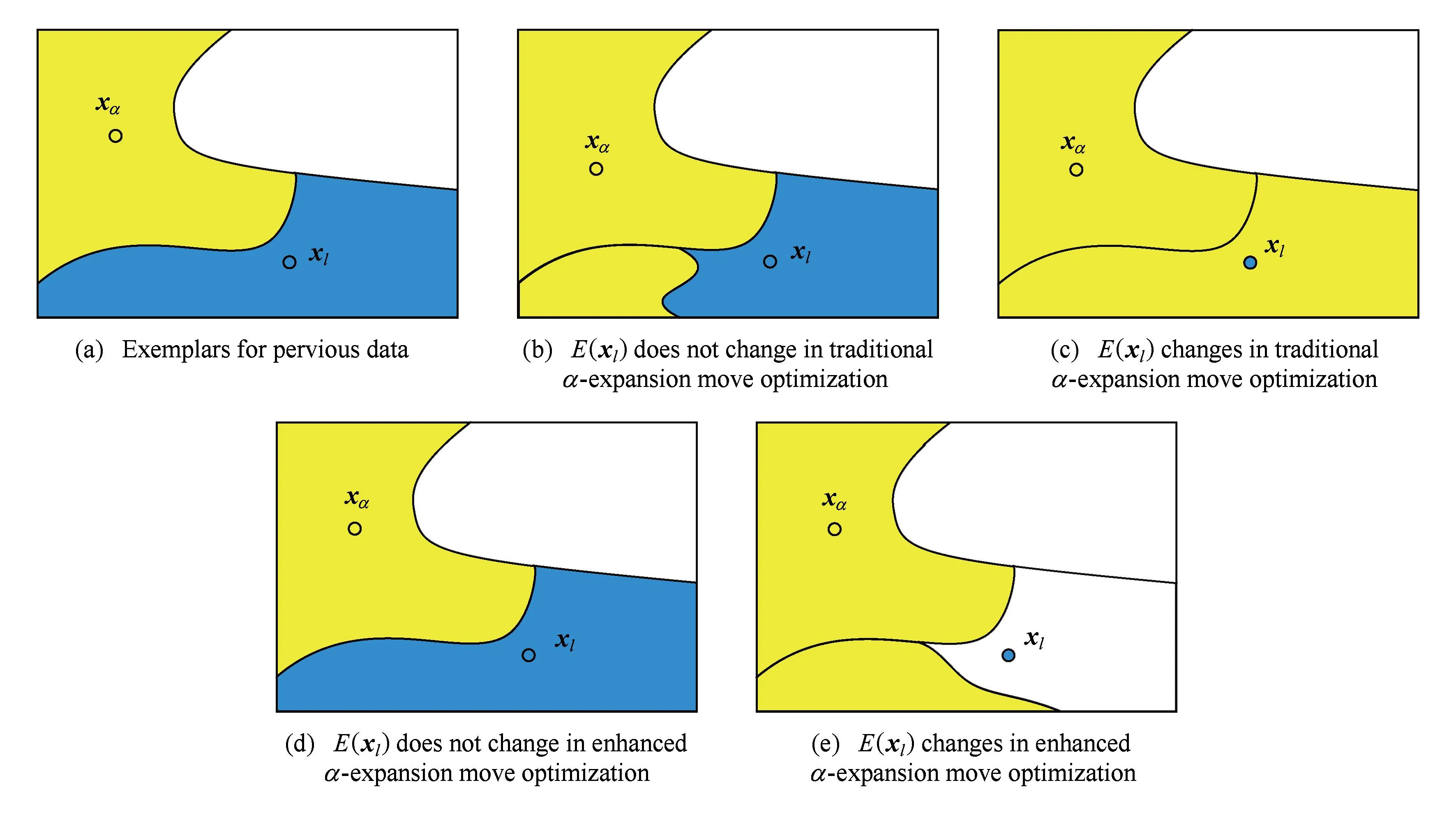
Fig. 3　Two types for when xαis an exemplar.图3　xα是代表点时2种α -expansion情况

情形1. 当xα是代表点时.

若E(xl)不改变，经典的α-expansion优化过程中将l簇中某些样本点的代表点变为xα，如图3(b)所示.改进的α-expansion优化算法则充分考虑到代表点集合有效的前提条件，即所有样本点已经选择当前代表点集合E中最有可能作为其代表点的样本作为代表点，因此在改进的α-expansion优化过程中，l簇中所有样本点的代表点均不会改变，如图3(d)所示.此时，能量函数损耗为0，即R=0.

若E(xl)改变，经典的α-expansion优化过程中将l簇中所有样本点的代表点变为xα，如图3(c)所示.由于改进的α-expansion优化算法扩张了代表点集合的搜索空间，因此l簇中的样本点将根据自身与代表点的相似性有选择地将代表点变成S(i)，如图3(e)所示.此时，能量函数的损耗可以表示为

(14)

因此，在改进的α-expansion优化过程中，若RXl<0，则进行图3(e)所示的扩张，即令E(xi)=S(i),∀xi∈Xl；否则进行图3(d)所示扩张，即代表点集合E不变化.

因此，当xα是代表点时，执行操作如算法1所述：

算法1. 情形1算法.

ifE(xα)=α

for每个其余代表点xl

计算l簇中每个样本点的次优代表点S(i)；

根据式 (14) 计算RXl；

ifRXl<0

l簇中样本点的代表点改为S(i)；

end if

end for

end if

情形2. 当xα是一般点时.

建立一个新的代表点集合E′=E，而E′(xα)=α，之后的优化过程与情形1一致，如图4所示.

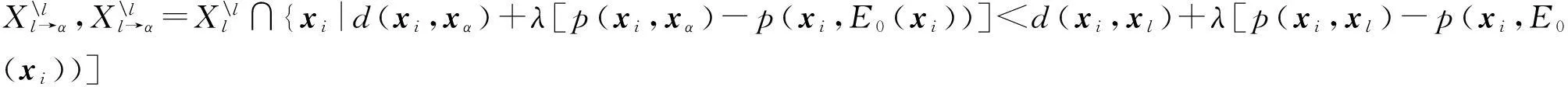
如图4(b)所示，经典的α-expansion优化过程中将该类样本的代表点变为xα，本文采用改进的α-expansion优化过程则将这部分样本的代表点变为S(i)，如图4(d)所示，相比经典的α-expansion优化算法，改进后的α-expansion算法保证样本点选择了更合理的代表点.此时，能量函数的损耗为

(15)

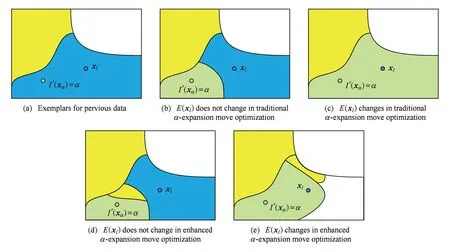
Fig. 4　Two types for when xαis not an exemplar.图4　xα不是代表点时2种α -expansion情况

如果E′(xl)改变，与情形1中图3(b)类扩张类似，在经典的α-expansion优化过程中，l簇中所有样本将选择xα作为代表点，如图4(c)所示.这显然是不合理的，因此，在改进的α-expansion优化中，l簇中所有样本都需要将他们的代表点改成S(i)，如图4(e)所示，此时能量函数的损耗为

(16)

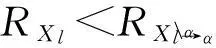
R2=d(xα,E(xα))-d(xα,xα)+λ[(p(xα,E(xα)))2-

2(p(xα,E(xα))-p(xα,xα))×p(xα,E0(xα))-

(17)

因此，当xα不是代表点时，执行操作如算法2所述：

算法2. 情形2算法.

ifE(xα)≠α

设置E′=E，而E′(xα)=α；

for每个其余代表点xl

计算l簇中每个样本点的次优代表点S(i)；

根据式 (16) 计算RXl；

l簇中样本点的代表点改为S(i)；

else

end if

end for

end if

2.4PDDE算法整体流程

根据2.3节相关优化理论及迭代公式推导所获取的学习规则，本节将给出PDDE聚类算法的具体步骤详见算法3.

算法3. PDDE算法.

输入：数据流数据X={X1,X2,…,Xk,…}每个样本自身相似性d(xi,xi)，正则化平衡因子λ；

输出：当前样本集中的有效代表点集合E.

步骤1. 使用AP算法或者EEM算法对该时刻前数据进行聚类，产生原始的代表点集合E0，令t=1；

步骤2. 随机产生α-expansion的顺序o，根据式(8)计算漂移数据选择其代表点的概率p(xi,E0(xi))，以及新的样本集内两两样本间的互为代表点的概率p(xi,xj)；

步骤3. 按照α-expansion的顺序o，如果xα是代表点，则执行算法1，否则执行算法2；

步骤4. 根据式(17)更新R2，若R2>0，E=E′，否则E不改变,转到步骤3；

步骤5.t=t+1；

步骤6. 算法收敛后，输出所得代表点集E.

3仿真实验

为了验证本文对数据流聚类任务的有效性，充分体现本文所提的PDDE聚类算法对漂移数据的聚类性能，本节将在人工合成数据集D31,Birch3及真实数据集Forest CoverType,KDD CUP99数据流上进行验证，并与AP算法以及EEM聚类算法进行比较，并对此结果进行适当的分析和解释.

为了公正地对聚类算法的聚类性能做出合理的评价，本文将采用2种评价指标进行算法的性能分析:

1) 聚类纯度(purity)[18]

(18)

其中，E={e1,e2,…,ek}是聚类算法得到的聚类结果，C={c1,c2,…,cj}是真实的类标集合.其取值范围为[0,1]，且随着数值的偏高显示出算法的性能越为优越.

2)SSQ(sum of square distance)[17]

(19)

其中，xk表示第k类的代表点，xi表示k类中第i个样本，d(xk,xi)表示两者的欧氏距离，SSQ的值越小聚类结果越紧密.

在本文的实验部分，各可调参数的设置均遵循文献[22,24,26]的计算策略，具体如表1所示.由于PDDE算法的初始化含有随机过程，因此在本文下面的实验部分中，如无特殊说明，均为在每个参数下10次算法完整运行后的均值所组成.

Table 1　Parameters of the PDDE Algorithm

实验环境：实验硬件平台为Intel®CoreTMi3-3240 CPU，其主频为3.40 GHz，内存为4 GB.操作系统为64位Windows 7，编程环境为MATLAB 2010a等.

3.1人工合成数据集实验

为了充分验证本文所提的PDDE算法对数据流数据的动态聚类效果，并能够体现数据随时间变化的特征，人工合成的数据集须遵循2项原则：

1) 原始数据应包含良好的聚类特征，即原始数据必须满足由其总结得到的聚类结果是可靠的，从而保证在此基础上对变化后的数据进行聚类能够提高其有效性；

2) 变化后的数据集与原始数据集应该具有相似性，或者共享部分数据，且其余数据有相似性.

本文采用的人工合成数据集D31[27]以及Birch3[28]是聚类算法中常用的验证算法聚类性能的数据集之一.其中D31数据集包括3 100个2维样本，共31类，其均匀分布如图5(a)所示；Birch3数据集则包括了10 000个2维样本，其聚类形状及样本分布均满足随机性.在实验过程中，认为数据中样本的输入顺序即为样本随着时间的流入顺序，在D31数据中，假设原始样本总数为1 000，单位时间内流入数据的个数为Sspeed=620，而针对Birch3数据集，假设原始样本总数为10 000，单位时间内流入数据的个数为Sspeed=1 000.由于目标样本数应该不足以保证传统聚类算法的聚类性能，因此实验中目标样本总数远小于原始样本总数.

如图5(a)所示，D31数据集中目标数据与原始数据无论在分布上存在较高的相似性，另一方面，图5(b)所示的Birch3数据集则体现了另一种数据间的相似性，即原始数据与目标数据共享部分数据.由本文之前的分析可知，PDDE算法能够处理包括这2种情况在内的数据流动态聚类问题.

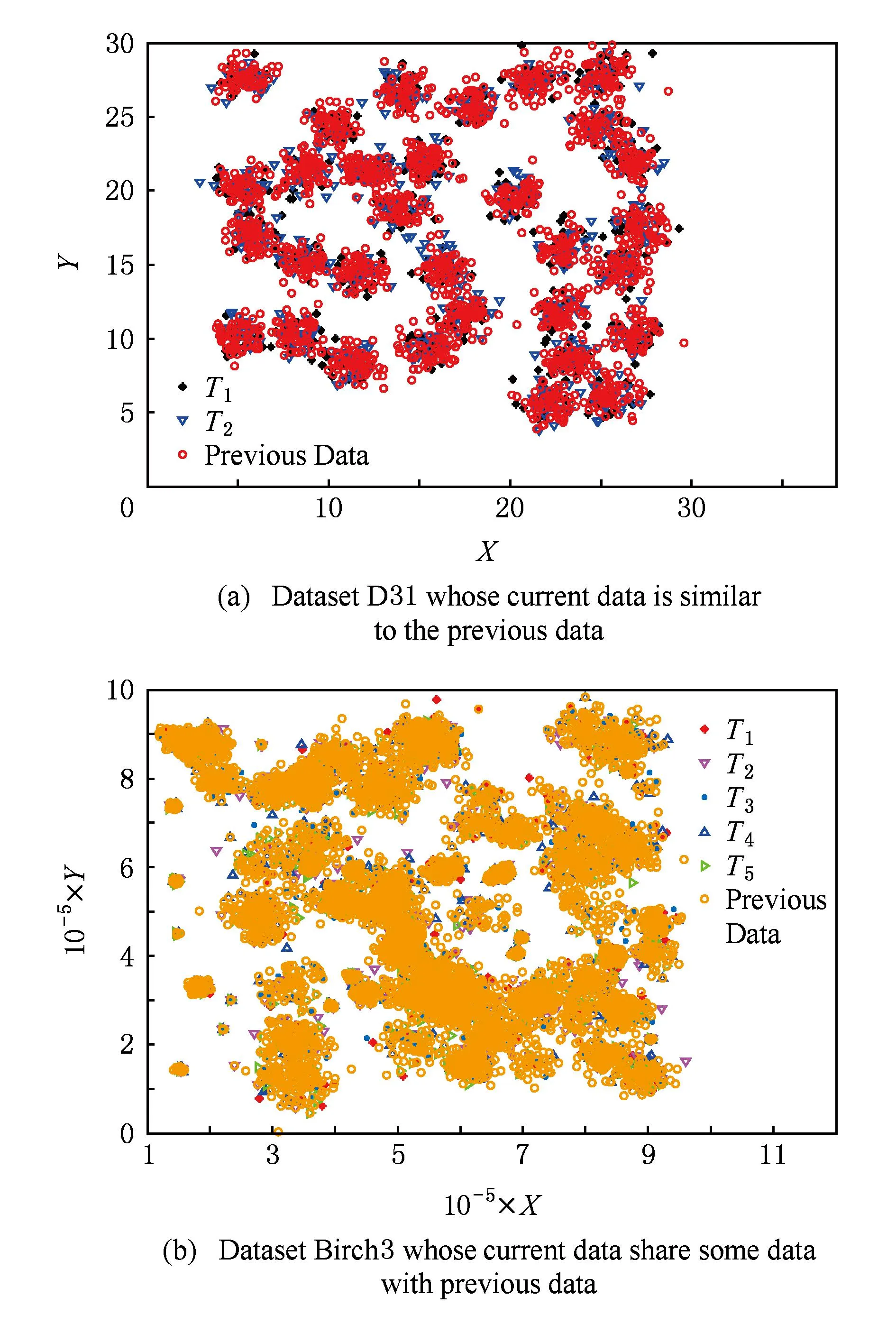
Fig. 5　Synthetic dataset.图5　人造数据集

由于Birch3数据集没有提供数据的标签信息，因此在Birch3实验中，除了SSQ评价标准外，本文还采用的聚类数作为聚类性能的评价标准.

另一方面，实验中涉及到的3种算法均包含了样本损耗，根据表1，3种算法中的样本损耗均为所有样本相似度的中值乘以[0.01,0.1,1,10,50,100]中的最优系数.根据实验结果，当聚类性能最优时，PDDE算法中该系数为0.1，而AP及EEM算法中该系数为1.

考虑到数据流动态聚类中不能对算法中涉及到的参数进行寻优，因此在实验中均在固定参数环境下对不同时刻的数据进行聚类，具体设置如下：在D31实验中，经过2个单位时间，因此实验结果中包括2个时刻T1和T2;而在Birch3实验中，数据经过5个单位时间，因此实验结果包括时刻T1,T2,T3,T4,T5的聚类结果.

人造数据集实验结果如表2及图6～9所示.其中表2及图6是基于D31数据流的实验结果，由于EEM针对该数据集的聚类性能极不稳定，因此表中没有列出EEM的聚类结果，图6(a)是AP算法针对原始数据的聚类结果，图6(b)及6(c)是PDDE算法分别对时刻T1和T2数据的聚类结果，图6(d)则为AP算法针对T1时刻数据聚类结果.图7～9则显示了Birch3的聚类结果，其中图7(a)是Birch3中原始数据的聚类结果，图7(b)～(d)则是某时刻PDDE聚类算法、EEM聚类算法和AP聚类算法的聚类结果，图8为3种算法在不同时刻聚类总数的比较，图9为PDDE算法在不同时刻聚类结果的SSQ性能比较.

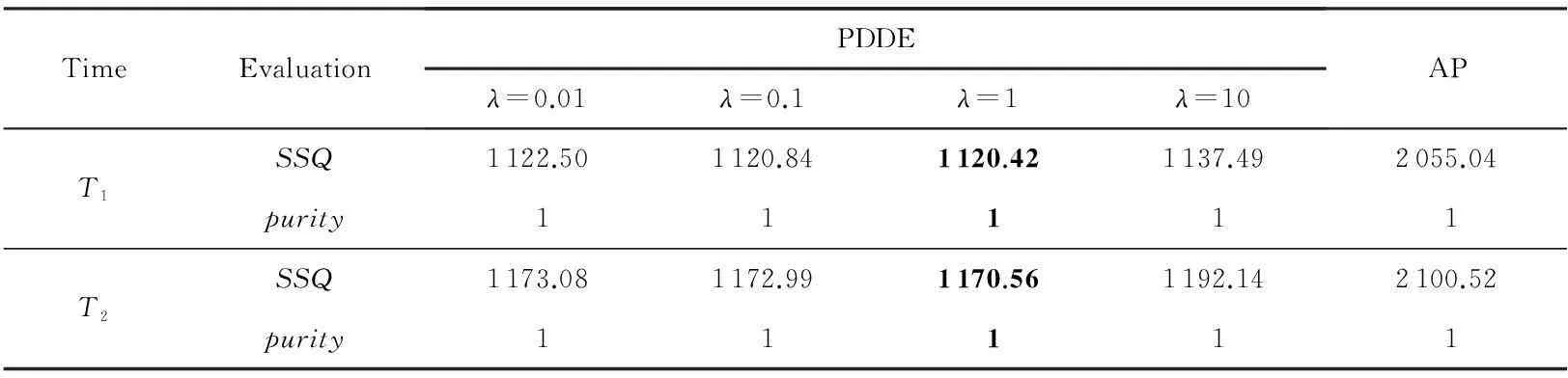
Table 2　Comparison of Different Algorithms Based on D31

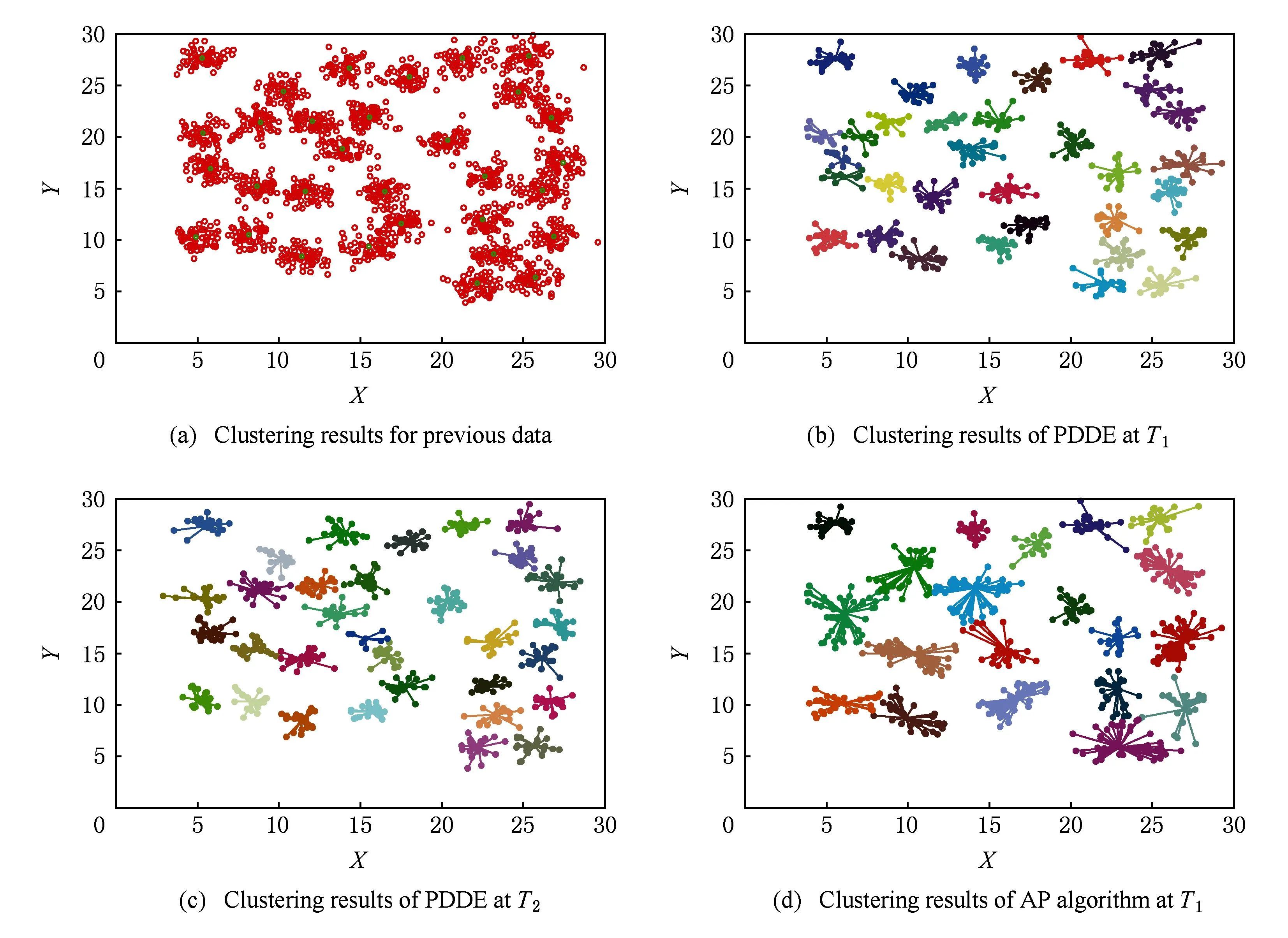
Fig. 6　Clustering results based on D31.图6　基于D31数据集聚类结果

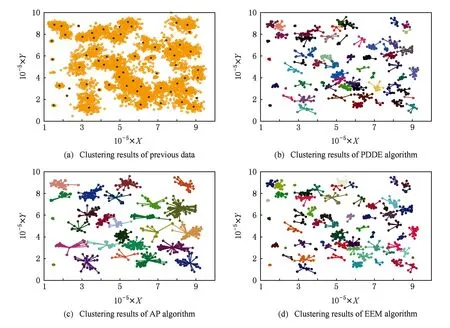
Fig. 7　Clustering results based on Brich3.图7　基于Birch3 数据集聚类结果

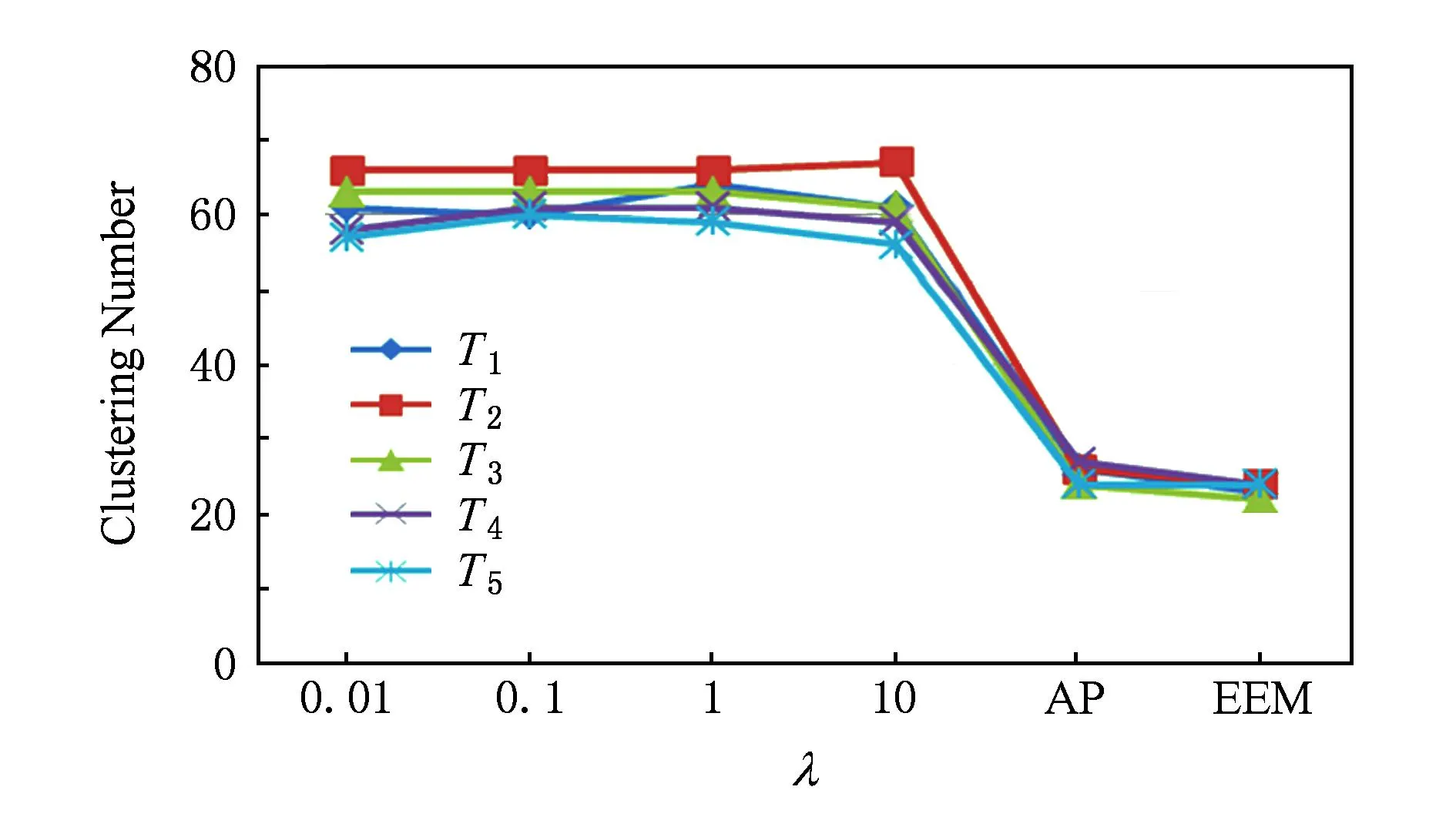
Fig. 8　Comparison of the number of clusters based on Birch3.图8　不同λ的聚类数比较(Birch3数据集)

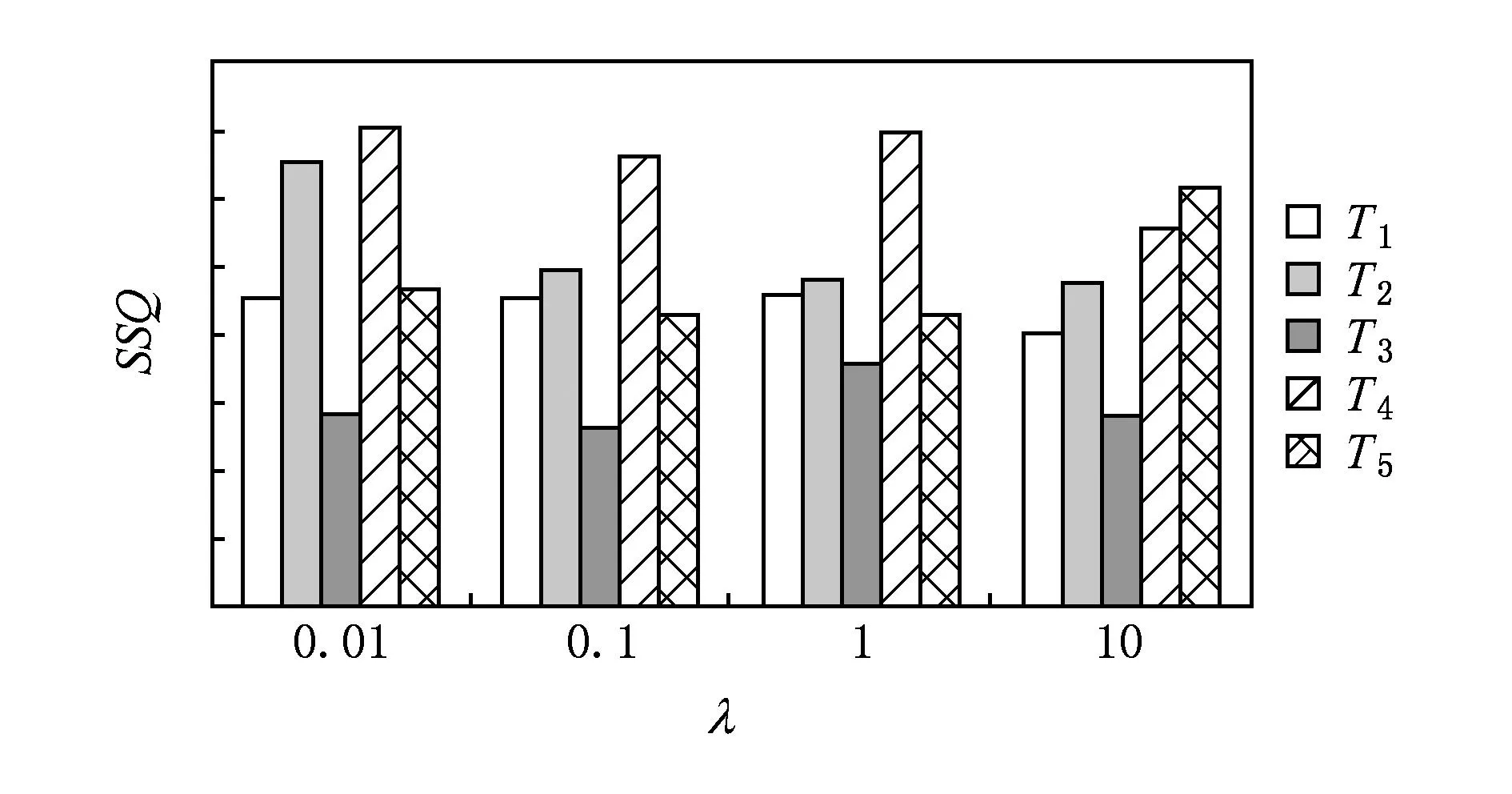
Fig. 9　Comparison of SSQ based on Birch3.图9　不同λ的SSQ比较(Birch3数据集)

分析表2及图6～9可知，在处理数据流动态聚类问题时,PDDE算法具有稳定、高效等特征.相比AP聚类及EEM聚类算法，PDDE聚类产生的结果更有效，尤其是当新进入的数据量不足，AP聚类算法及EEM聚类算法根据有限的样本量产生的聚类结果实际上与样本本身的分布存在较大的差异，而PDDE算法借助于原始数据的聚类结果，在样本量不足的情况下仍能得到具有较高可信度的聚类结果.图6、图7直观地表明，由于原始数据可靠的聚类结果，PDDE算法得到的聚类结果更加高效.

3.2真实数据集

在基于真实数据集的实验中，使用2种广泛使用的真实数据流，KDD CUP99和Forest CoverType.其中KDD CUP99是网络入侵检测数据，由MIT林肯实验室花费2周时间检测而成.数据集中共包含494 031个样本，每个样本41维，与文献[19]中实验设置一致，实验中使用其中的34维连续属性，所有样本被分为五大类.为了构造时序性数据，在实验过程中，认为数据中样本的输入顺序即为数据中随着时间流入的数据.对KDD CUP99数据做如下改造：初始数据为N0=10 000，每个单位时间内流入的数据个数为Sspeed=2 000.为了保证新进入的数据与原始数据具有充分的相似性，其中1 000个数据是从原始数据以及之前流入的数据中随机选择的，另外1 000个数据为数据集中样本的顺序进入，即原始数据与新数据共享部分数据.

Forest CoverType数据集来自常用的UCI数据集，共包含581 012个样本，每个样本24维，与文献[18]一致，实验中采用了其中10维连续属性，Forest CoverType数据集将数据分为了七大类.与KDD CUP99一样，认为数据中样本的输入顺序即为数据中随着时间流入的数据.对Forest CoverType数据做如下改造：初始数据为N0=1 000，每个单位时间内流入的数据个数为Sspeed=200，其中100个数据是从原始数据以及之前流入的数据中随机选择的，另外100个数据为数据集中样本的顺序进入，即原始数据与新数据共享部分数据.由于EEM算法在该数据集聚类结果非常不稳定，因此将不考虑EEM的聚类结果.

实验中均为经过5个单位时间，对每个单位时间内新进入的数据进行聚类，并使用聚类纯度，即式(18)作为聚类性能的评价标准.实验中涉及到的参数环境如表1所示.由表1可知，3种算法中的样本损耗均为所有样本相似度的中值乘以[0.01,0.1,1,10,50,100]中的最优系数.实验证明，当聚类性能最优时，PDDE算法中样本损耗为100，而AP及EEM算法中样本损耗为50.具体实验结果如表3所示，图10、图11所示，说明PDDE算法能够高效地处理数据流动态聚类问题.

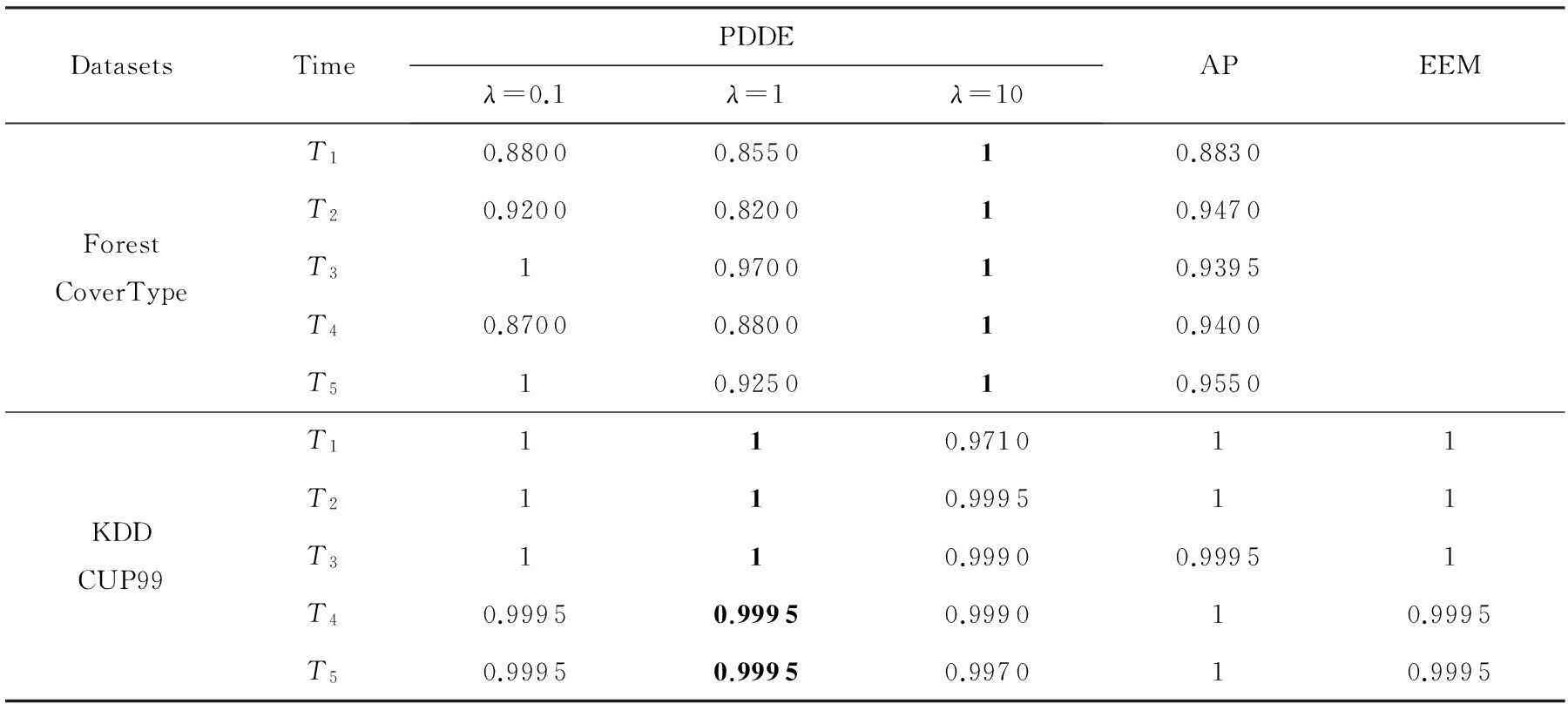
Table 3　Comparison of Different Algorithms Based on Real Dataset

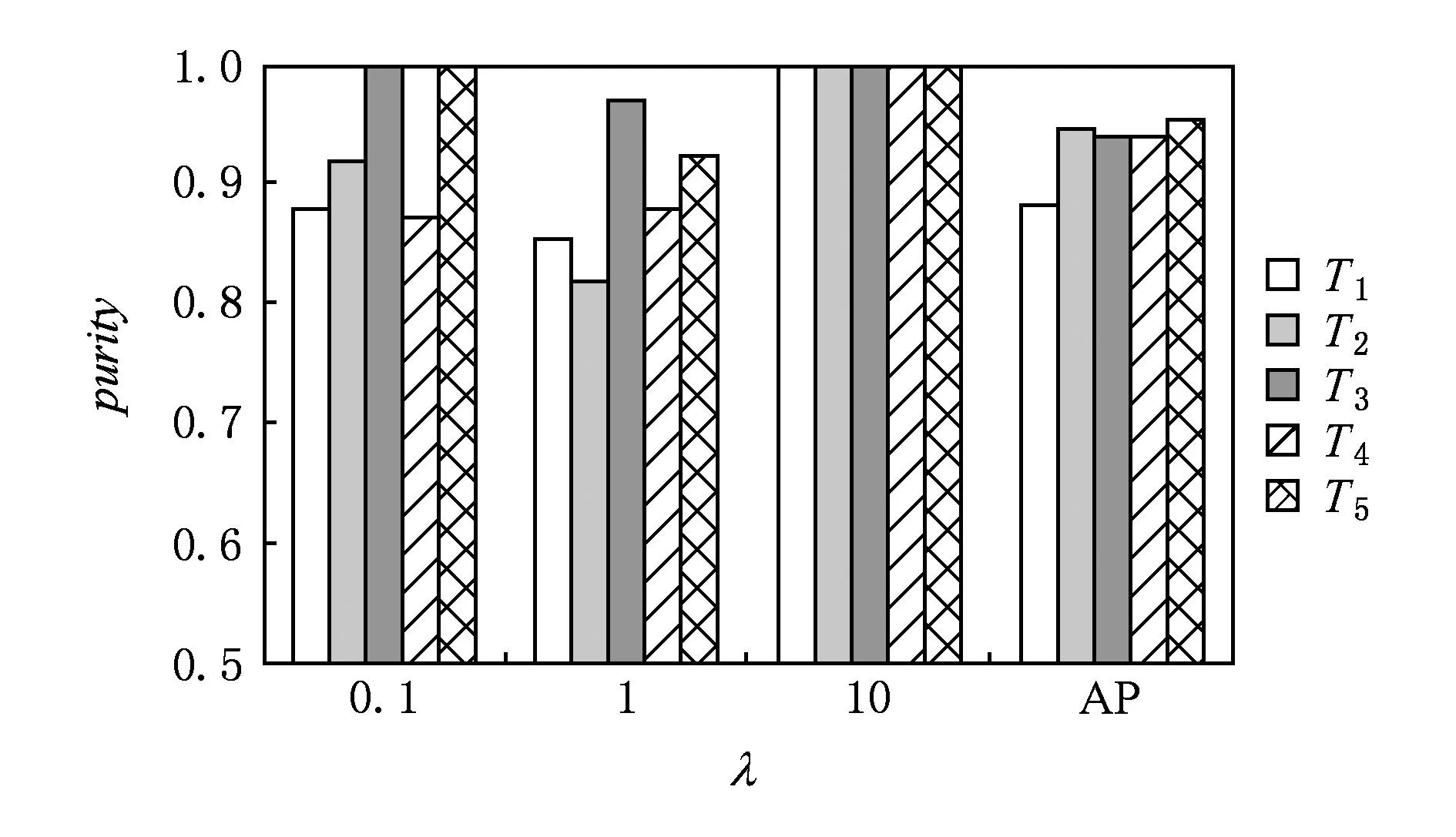
Fig. 10　Comparison of clustering effectiveness based on Forest CoverType.图10　基于Forest CoverType数据集聚类性能比较

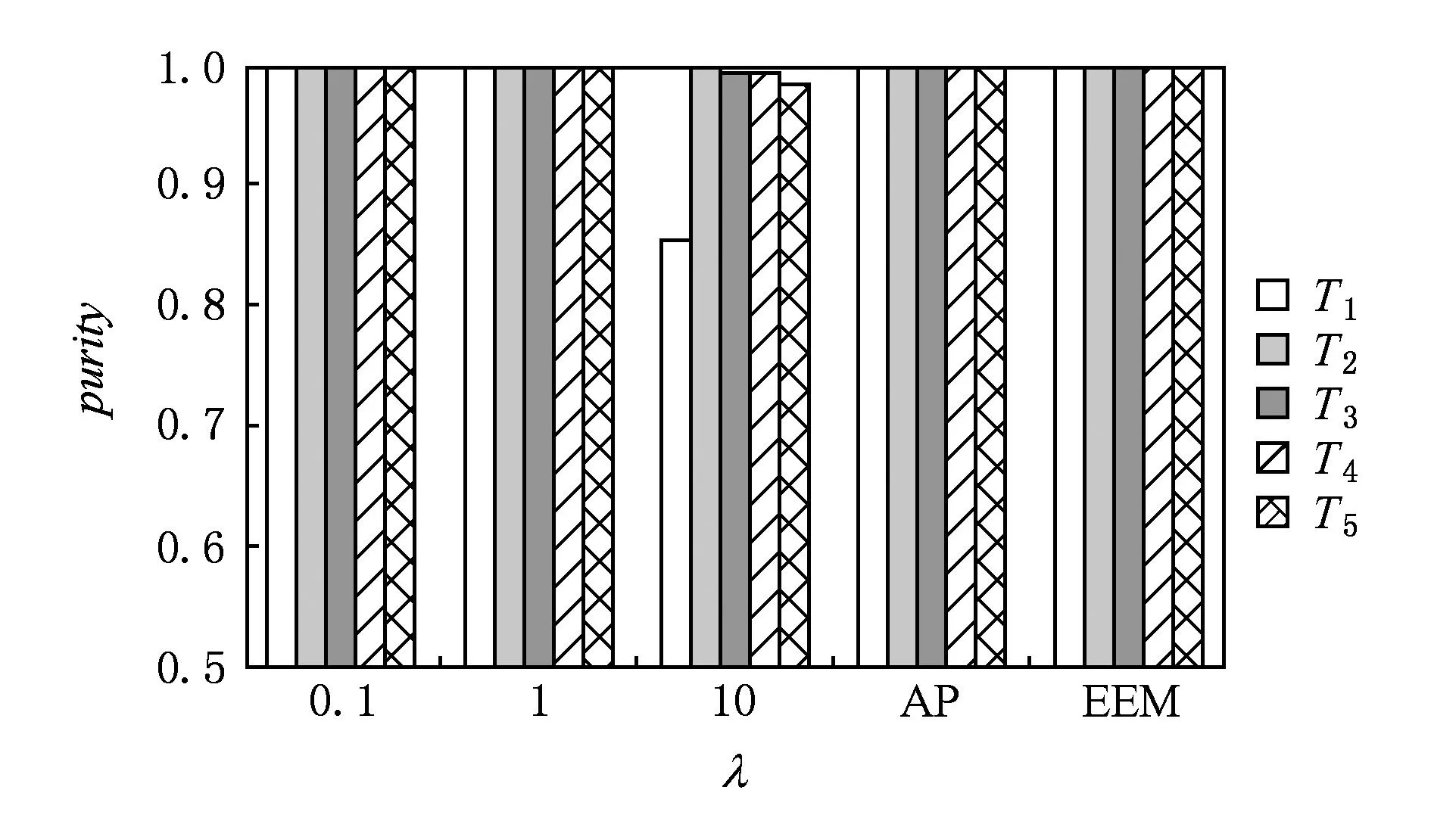
Fig. 11　Comparison of clustering effectiveness based on KDD CUP99.图11　基于KDD CUP99数据集聚类性能比较

3.3实验结果分析

分析3.1节和3.2节中基于人造数据集D31,Birch3和真实数据集Forest Covertype,KDD CUP99的实验结果，关于PDDE动态数据流聚类算法可以得到3个结论：

1) PDDE算法能够稳定、高效地处理数据流的动态聚类问题.在借助原始数据可靠的聚类结果后，通过PDDE算法得到的聚类结果比传统的聚类算法更加有效.

2) 正则化平衡因子λ对实验结果影响较大.

3) 经过多个单位时间后，由于PDDE算法借鉴了原始数据的聚类结果，在参数固定的情况下，聚类性能仍然非常稳定，并优于传统的基于代表点聚类算法AP算法和EEM算法.

4结论

本文针对当前基于代表点的聚类算法不具有处理数据流动态聚类问题的能力，首先从概率角度给出了AP算法和EEM算法的联合目标函数，利用概率框架来度量样本点选择另一个样本为代表点的可能性，以及代表点集合的先验概率来度量该代表点集合的稳定性.由于该理论能够直接度量某样本与其代表点之间的相似性，为解决数据流的动态聚类问题提供了前提条件.另一方面，本文进一步使用Graph Cuts优化算法求解能量函数，进而保证了算法的聚类有效性.

此外，本文的另一大贡献在于改进了AP及EEM算法的联合目标函数，使之能够适用于时序数据动态聚类问题.通过样本与其代表点之间的概率，借助于原始样本与其代表点之间的概率关系，引入正则化平衡因子保证漂移后的样本所选择的代表点仍然能够与之前的代表点保持较高的相似性，进而提出了一种新的适用于时序数据聚类的有效算法——PDDE算法.同时，由于引入了概率，PDDE算法能够处理原始数据与新数据之间的2种相似性关系，即不论原始数据与新数据是否共享部分数据，PDDE算法都能够完成数据流动态聚类.通过在人工合成数据集D31和Birch3以及常用的真实数据集KDD CUP99,Forest CoverType的实验结果，均显示本文方法较AP聚类以及EEM算法具有更稳定、高效的聚类性能.

参考文献

[1]Yu S, Tranchevent L C, Liu X, et al. Optimized data fusion for kernelK-means clustering[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2012, 34(5): 1031-1039

[2]Jing L, Ng M K, Huang J Z. An entropy weightingk-means algorithm for subspace clustering of high-dimensional sparse data[J]. IEEE Trans on Knowledge and Data Engineering, 2007, 19(8): 1026-1041

[3]Zhu L, Chung F L, Wang S. Generalized fuzzyC-means clustering algorithm with improved fuzzy partitions[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(3): 578-591

[4]Hall L O, Goldgof D B. Convergence of the single-pass and online fuzzyc-means algorithms[J]. IEEE Trans on Fuzzy Systems, 2011, 19(4): 792-794

[5]Wang S, Chung F L, Deng Z H. Robust maximum entropy clustering algorithm with its labeling for outliers[J]. Soft Computing, 2006, 10(7): 555-563

[6]Karayiannis N B. MECA: Maximum entropy clustering algorithm[C]Proc of the 3rd IEEE Conf on Fuzzy Systems. Piscataway, NJ: IEEE, 1994: 630-635

[7]Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55

[8]Wu Yingjie, Tang Qingming, Ni Weiwei, et al. A clustering hybrid based algorithm for privacy preserving trajectory data publishing[J]. Journal of Computer Research and Development, 2013, 50(3): 578-593 (in Chinese)(吴英杰, 唐庆明, 倪巍伟, 等. 基于聚类杂交的隐私保护轨迹数据发布算法[J]. 计算机研究与发展, 2013, 50(3): 578-593)

[9]Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976

[10]Murphy K P, Weiss Y, Jordan M I. Loopy belief propagation for approximate inference: An empirical study[C]Proc of the 15th Conf on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufmann, 1999: 467-475

[11]Tappen M F, Freeman W T. Comparison of graph cuts with belief propagation for stereo, using identical MRF parameters[C]Proc of the 9th IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2003: 900-906

[12]Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222-1239

[13]Zheng Yun, Chen Pei. Clustering based on enhancedα-expansion move[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 25(10): 2206-2216

[14]Guha S, Meyerson A, Mishra N, et al. Clustering data streams: Theory and practice[J]. IEEE Trans on Knowledge and Data Engineering, 2003, 15(3): 515-528

[15]O’Callaghan L, Mishra N, Meyerson A, et al. Streaming-data algorithms for high-quality clustering[C]Proc of the 18th IEEE Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2002: 685-694

[16]Aggarwal C C, Han J, Wang J, et al. A framework for clustering evolving data streams[C]Proc of the 29th Int Conf on Very Large Data Bases. San Francisco: Morgan Kaufmann, 2003: 81-92

[17]Aggarwal C C, Han J, Wang J, et al. A framework for projected clustering of high dimensional data streams[C]Proc of the 30th Int Conf on Very Large Data Bases. San Francisco: Morgan Kaufmann, 2004: 852-863

[18]Cao F, Ester M, Qian W, et al. Density-based clustering over an evolving data stream with noise[C]Proc of 2006 SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2006: 328-339

[19]Yu Yanwei, Wang Qin, Kuang Jun, et al. An on-line density-based clustering algorithm for spatial data stream[J]. Acta Automatica Sinica, 2012, 38(6): 1061-1059 (in Chinese)(于彦伟, 王沁, 邝俊, 等. 一种基于密度的空间数据流在线聚类算法[J]. 自动化学报, 2012, 38(6): 1051-1059)

[20]Yu Xiang, Yin Guisheng, Xu Xiandong, et al. A data stream subspace clustering algorithm based on region partition[J]. Journal of Computer Research and Development, 2014, 51(1): 88-95 (in Chinese)(于翔, 印桂生, 许宪东, 等. 一种基于区域划分的数据流子空间聚类方法[J]. 计算机研究与发展, 2014, 51(1): 88-95)

[21]Deng Z H, Choi K S, Chung F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern Recognition, 2010, 43(3): 767-781

[22]Sun A, Zeng D D, Chen H. Burst detection from multiple data streams: A network-based approach[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2010, 40(3): 258-267

[23]Zhu Y, Shasha D. Efficient elastic burst detection in data streams[C]Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York; ACM, 2003: 336-345

[24]Jiang Yizhang, Deng Zhaohong, Wang Jun, et al. Transfer generalized fuzzyc-means clustering algorithm with improved fuzzy partitions by leveraging knowledge[J]. Pattern Recognition and Artificial Intelligence, 2013, 10(26): 975-984 (in Chinese)(蒋亦樟, 邓赵红, 王骏, 等. 基于知识利用的迁移学习一般化增强模糊划分聚类算法[J]. 模式识别与人工智能, 2013, 10(26): 975-984)

[25]Kolmogorov V, Zabih R. What energy functions can be minimized via graph cuts?[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(2): 147-159

[26]Huang Chengquan, Wang Shitong, Jiang Yizhang. A new fuzzy clustering algorithm with entropy index constraint[J]. Journal of Computer Research and Development, 2014, 51(9): 2117-2129 (in Chinese)(黄成泉, 王士同, 蒋亦樟. 熵指数约束的模糊聚类新算法[J]. 计算机研究与发展, 2014, 51(9): 2117-2129)

[27] Veenman C J, Reinders M J T, Backer E. A maximum variance cluster algorithm[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2002. 24(9): 1273-1280

[28]Zhang T, Ramakrishnan R, Livny M. BIRCH: A new data clustering algorithm and its applications[J]. Data Mining and Knowledge Discovery, 1997, 1 (2): 141-182

Bi Anqi, born in 1989. PhD candidate. Her current research interests include pattern recognition, intelligent computation and their application.

Dong Aimei, born in 1978. PhD candidate at the School of Digital Media, Jiangnan University, and lecturer at Qilu University of Technology. Her research interests include artificial intelligence, pattern recognition, and machine learning.

Wang Shitong, born in 1964. Professor and PhD supervisor. Senior member of China Computer Federation. Received his MS degree in computer science from Nanjing University of Aeronautics and Astronautics, China, in 1987. His current research interests include artificial intelligence, pattern recognition, fuzzy system, medical image processing, data mining, and intelligent computation and their applications.

A Dynamic Data Stream Clustering Algorithm Based on Probability and Exemplar

Bi Anqi1, Dong Aimei1,2, and Wang Shitong1

1(SchoolofDigitalMedia,JiangnanUniversity,Wuxi,Jiangsu214122)2(SchoolofInformation,QiluUniversityofTechnology,Jinan250353)

AbstractWe propose an efficient probability drifting dynamic α-expansion clustering algorithm, which is designed for data stream clustering problem. In this paper, we first develop a unified target function of both affinity propagation (AP) and enhanced α-expansion move (EEM) clustering algorithms, namely the probability exemplar-based clustering algorithm. Then a probability drifting dynamic α-expansion (PDDE) clustering algorithm has been proposed considering the probability framework. The framework is capable of dealing with data stream clustering problem when current data points are similar with pervious data points. In the process of clustering, the proposed algorithm ensures that the clustering result of current data points is at least comparable well with that of previous data points. What’s more, the proposed algorithm is capable of dealing with two kinds of similarities between current and previous data points, that is whether current data points share some points with previous data points or not. Besides, experiments based on both synthetic (D31, Birch 3) and real-world dataset (Forest Covertype, KDD CUP99) have indicated the capability of PDDE in clustering data streams. The advantage of the proposed clustering algorithm in contrast to both AP and EEM algorithms has been shown as well.

Key wordsdata stream; energy function; probability; optimization algorithm; dynamic clustering

收稿日期：2014-12-23；修回日期：2015-06-02

基金项目：国家自然科学基金项目(6127220);山东省高等学校科技计划项目(J14LN05);江苏省普通高校研究生科研创新计划基金项目(KYLX_1124)

中图法分类号TP391

This work was supported by the National Natural Science Foundation of China (6127220), the Project of Shandong Province Higher Educational Science and Technology Program (J14LN05), and Jiangsu Graduate Student Innovation Projects (KYLX_1124).