一种大规模分类数据聚类算法及其并行实现

丁祥武　郭　涛　王　梅　金　冉

1(东华大学计算机科学与技术学院　上海　201620)2(浙江万里学院计算机与信息学院　浙江宁波　315100)(dingxw@dhu.edu.cn)

一种大规模分类数据聚类算法及其并行实现

丁祥武1郭涛1王梅1金冉2

1(东华大学计算机科学与技术学院上海201620)2(浙江万里学院计算机与信息学院浙江宁波315100)(dingxw@dhu.edu.cn)

摘要CLOPE算法在大规模、稀疏、高维的分类数据集的聚类上取得了很好的聚类效果.然而该算法受输入数据的顺序影响，难以获得稳定且全局最优的聚类结果.因此提出一种基于等分划分再排列思想的p -CLOPE算法对这一缺陷进行改进.在p -CLOPE算法的每一轮迭代过程中，对输入数据集等分为p部分再排列生成不同顺序的p!份数据集，对这些数据集分别聚类并选取最优的聚类结果作为下一轮迭代的输入.为了降低上述过程的时间复杂度，提出了一种中间结果复用策略，较大程度地提高了聚类速度.最后，在Hadoop平台上实现了一个包含p -CLOPE相关算法的开源聚类工具.实验表明：p -CLOPE算法比CLOPE算法取得了更优的聚类结果.对蘑菇数据集，当CLOPE算法取得最优聚类结果时，p -CLOPE比CLOPE取得了高35.7%的收益值；在处理大量数据时，并行p -CLOPE比串行p -CLOPE极大地缩短了聚类时间，并在计算资源充足时，取得了接近p!倍的加速比.

关键词分类数据；CLOPE；p -CLOPE；并行聚类；MapReduce

传统的针对数值数据的聚类算法虽然在不断取得突破[1]，但并不适合处理分类数据[2].分类数据由非数值的属性组成.对分类数据快速且准确地聚类在零售业、电子商务、医疗诊断、生物信息学等领域都有大量应用.因此，研究分类数据的聚类算法具有重要意义.

然而，这些领域的数据通常具有高维度、稀疏、数据量大等特征，要对这种分类数据进行快速且准确地聚类通常非常困难.分类数据聚类算法k-modes[3]是对基于距离的数值数据聚类算法k-means[4]的扩展，采用0-1差异度来代替k-means算法中的距离，但没能充分考虑2个属性间的相似性，也没有从全局的角度考虑2条交易间的相似性.层次聚类方法ROCK[5]采用公共邻居数(链接)作为评价交易间相关性的度量标准.用于界定2条交易是否为邻居的相似度阈值θ需要预先指定，但很难给出恰当的阈值，另外还要求用户事先选定聚类簇数k.LargeItem[6]算法通过迭代优化一个全局评估函数来实现对大量分类数据的聚类，其最小支持度θ和权重w很难确定.CLOPE[7]算法在大规模、稀疏、高维数据集的聚类上取得了较好的聚类效果，该算法提出一个全局评估函数，通过一个簇的直方图中的高与宽的比率来表示这个簇内交易的重叠程度.CLOPE的运行速度比LargeItem和ROCK更快，聚类质量比LargeItem更优，与设定了合适参数值的ROCK算法接近[7].SCLOPE[8]和σ-SCLOPE[9]是CLOPE应用在数据流上的聚类算法，牺牲了一些聚类的准确性.FUZZY CLOPE[10]提出了一种修正的划分模糊度，用来实现对CLOPE算法中的排斥因子r的自动优选.但是，这些研究都没有涉及一个问题：即数据集中交易的输入顺序会对聚类结果产生影响，不同的输入顺序可能会得到不一致的聚类结果.这一缺陷将导致CLOPE算法不能取得稳定且最优的聚类结果.

本文提出了p-CLOPE算法，它采用一种等分划分再排列输入数据的思想对上述缺陷进行改进.为了降低p-CLOPE算法的时间复杂度，提出了一种中间结果复用策略，通过该策略可以较大程度地提高聚类速度.最后，在Hadoop平台上用MapReduce并行编程模型实现了p-CLOPE算法的并行化，并分析了时间与空间复杂度和加速比.实验表明:p-CLOPE算法能比CLOPE算法取得更优的聚类结果，也取得了很好的加速比.

1CLOPE算法及其缺陷

1.1CLOPE算法

分类数据聚类算法CLOPE[7]以簇的直方图的高宽比作为全局评估函数(也称全局收益函数).随着每一簇内数据重合度的增多，代表簇的统计直方图的高宽比也逐渐增加.所有簇的直方图的高宽比之和称为全局收益值.当全局收益值达到最大时，所对应的聚类被认为是最优的.

定义1[7]. 分类数据集D是一组交易数据的集合{t1,t2,…,tn}.每条交易数据是一些属性项的集合{i1,i2,…,im}.一个聚类{C1,C2,…,Ck}是{t1,t2,…,tn}的一个划分，也就是说C1∪C2∪…∪Ck={t1,t2,…,tn}而且对任意1≤i,j≤k，满足Ci≠∅，且Ci∩Cj=∅.每一个Ci叫作一个簇，n，m，k分别表示交易的条数、属性项的个数、簇的个数.

给定一个簇C，可以找到这个簇中所有的不同属性项，一个属性项出现的频率表示有多少条交易包含这个属性项，用D(C)表示簇C中不同属性项的集合，用Occ(i,C)表示属性项i在簇C中出现的频率.这样可以画出簇C的直方图，用属性项表示X轴，用每个属性项出现的频率表示Y轴[7].定义一个簇C的直方图的面积S(C)和宽度W(C)为[7]

(1)

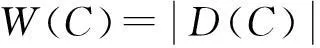
(2)

簇的高定义为H(C)=S(C)W(C)，全局评估函数定义为

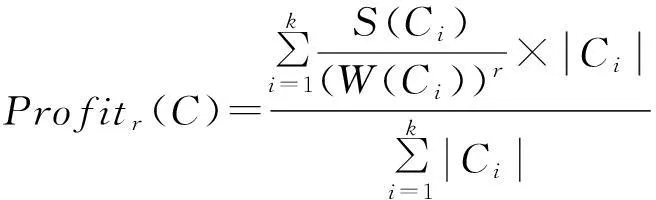
(3)

其中，排斥因子r是一个正实数，用来控制簇内交易间的相似程度.当r较大时，簇内的交易必须有较多的公共项；相反，较小的r可用来对稀疏数据分组.通过调整排斥因子r的大小可以得到不同的簇个数，r越大，簇的个数越多.对于每个确定的r都可以找到一个划分C使得收益值Profit(C)最大.具体的算法如下：

算法1. CLOPE算法[7].

① while 未到数据文件尾部

② 读下一条交易〈t,unknown〉；

③ 将t放入一个使收益最大的现有簇或新簇Ci中;

④ 将〈t,i〉写回数据集中;

⑤ repeat

⑥ 重新回到数据文件头;

⑦moved=false；

⑧ while 未到数据文件尾部

⑨ 读下一条交易〈t,i〉；

⑩ 移动t到一个使收益最大的现有簇或新簇Cj中;

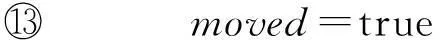
1.2CLOPE算法的缺陷分析

对于一个特定的排斥因子r，CLOPE算法的目的是找一个收益值Profit(C)最大的聚类.但是实际上我们发现CLOPE算法并不能找到收益值最大的聚类，因为它的聚类结果会受数据集中交易的输入顺序的影响，交易的顺序不同时聚类结果可能不一致.也就是说CLOPE算法不能得到稳定的聚类结果，而且这个聚类结果通常不是最优的.

这里举例来说明这一问题：对数据集D={abd,bcd,acd,ab,bc,ac}，当排斥因子r=2.0时，如果数据按照从左到右(abd→bcd→acd→ab→bc→ac)的顺序输入给CLOPE算法，那么得到的聚类{D}只有一个簇，其收益值为0.938.但是，如果按照从右到左(ac→bc→ab→acd→bcd→abd)的顺序输入，那么得到的聚类{{ab,abd}，{bc,bcd}，{ac,acd}}有3个簇，此时收益值为0.556.从以上的例子可以看出，输入交易的顺序不同时，聚类的结果可能不同.但是由于在默认的情况下，CLOPE算法只是按交易的原始顺序对数据集进行聚类，这样很有可能得不到最优的聚类结果.

上述例子用到的数据集D只有6条交易，我们通过穷举所有的输入顺序进行计算，发现只有2种聚类结果.而对一个实际待聚类的数据集，其数据量很大，在有限的计算能力下，穷举所有的输入顺序，其计算时间是很难接受的.本文接下来提出一种先对数据划分再排列划分块的思想来克服这一缺陷.

2p-CLOPE算法

2.1算法设计

针对CLOPE算法的缺陷，本文的改进思想是对原始数据形成多种输入顺序，对每种顺序的数据分别聚类，然后从中选择最优的聚类作为最后的输出.本文提出等分再排列的思想来形成不同顺序的数据.具体来说是先将要聚类的数据集D进行等分划分，再进行排列，目的是打乱输入数据的顺序.如果将D等分为p部分，那么可产生p!种不同的排列，将重新排列后的数据集分别定义为Di(1≤i≤p!)，每一份数据集中交易的集合是相同的，只是交易的顺序不同.对于得到的p!份数据集，我们可有2种处理方案:1)对每一份数据集Di先执行CLOPE算法的全过程，然后再比较对每一份数据集聚类的收益值，选出收益值最大的聚类结果作为最终聚类结果；2)用CLOPE算法对p!份数据集分别执行一次迭代，然后对这些迭代中最优的聚类结果重新等分划分再排列作为下一次迭代的输入，如此迭代，直至全局最优聚类划分不再变化时，整个聚类过程结束.第2种方案能达到每一次迭代结果的最优，而且对最优的聚类划分代表的数据集又重新划分排列成p!份数据集，因而它对交易的顺序打乱得更充分，可以取得比第1种方案全局更优的聚类结果，而且所需要的迭次代数更少，整个聚类过程所需时间当然更少.因而，我们选择第2种方案，具体步骤如下：

阶段1. 对于每一份数据集Di，依次读取它的每一条交易t，决定将t放入一个已经存在的簇还是放入一个新的簇中，这取决于哪种情况下收益值将更大.每一个簇的收益值定义为

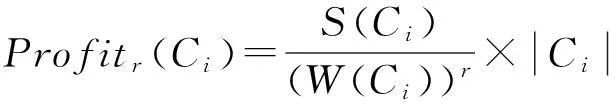
(4)

通过比较将t放入已有的各簇和放入一个新的簇所产生的收益值增量的大小来判断将t放入已有的某簇中还是放入一个新的簇中.这样每一份数据集Di都会被划分成一些簇，而且每条交易有了对应的簇编号.阶段1结束后，每个数据集Di代表了一个聚类，计算各个聚类的收益值Profitr(C).比较各个聚类的收益值，选出收益值最大的数据集Dm.

阶段2. 将Dm等分划分为p份，再排列为p!份数据集{D1,D2,…,Dp!}，对每一份数据集Di执行原始CLOPE算法的阶段2，即依次读取它的每一条交易t，将这条交易从原来的簇中移除，再根据簇收益值的增量大小选择放入某个已有的簇或者放入一个新的簇，如果这条交易现在放入的簇和原来所在的簇是同一个簇，则表示这个交易没有移动.如果一个数据集Di中所有的交易都没有移动，则表示Di对应的整个聚类划分不再变化.再次计算每个数据集的收益值，从中选出全局收益值最大的数据集Dm.如果在某一轮迭代中，Dm中没有交易移动，则程序结束，Dm对应的聚类划分就是最终所求的聚类划分.否则，重复执行以上阶段2的步骤，直到迭代结束.

由于本文的改进思想中引入了划分参数p，因此将新的算法命名为p-CLOPE.

2.2划分参数p

对于我们新引入的划分参数p，它是一个正整数.理论上，如果p等于数据集中总的交易条数n，那么划分的每一部分都只包含一条交易，这样的排列是一个全排列，能得到交易的各种顺序组合.但实际上，当n很大时，由于受计算能力和存储空间的限制，将无法实现这种情况，因为p!是一个增长非常快的函数.在我们设计的p-CLOPE算法里，将p设定为用户可以指定的参数，根据实际的计算能力和存储空间来设定.实际上从第3节的实验中可以看到：当p=4时已经可以达到非常好的聚类效果,当p=1时p-CLOPE退化为CLOPE.

2.3中间结果的复用

将待聚类的数据集进行等分划分、再进行排列，目的是遍历划分块所构成的全排列，而我们发现这个计算过程中存在大量相同的中间结果，充分利用可重用的中间结果可以很大程度地提高聚类的速度.以p=4为例，将待聚类的数据集划分为4等份，标记为A，B，C，D.以A开始的排列可以用如图1所示的树来表示(以B，C，D开始的排列类似).每一种排列就是从根节点到叶子节点顺序遍历的节点.

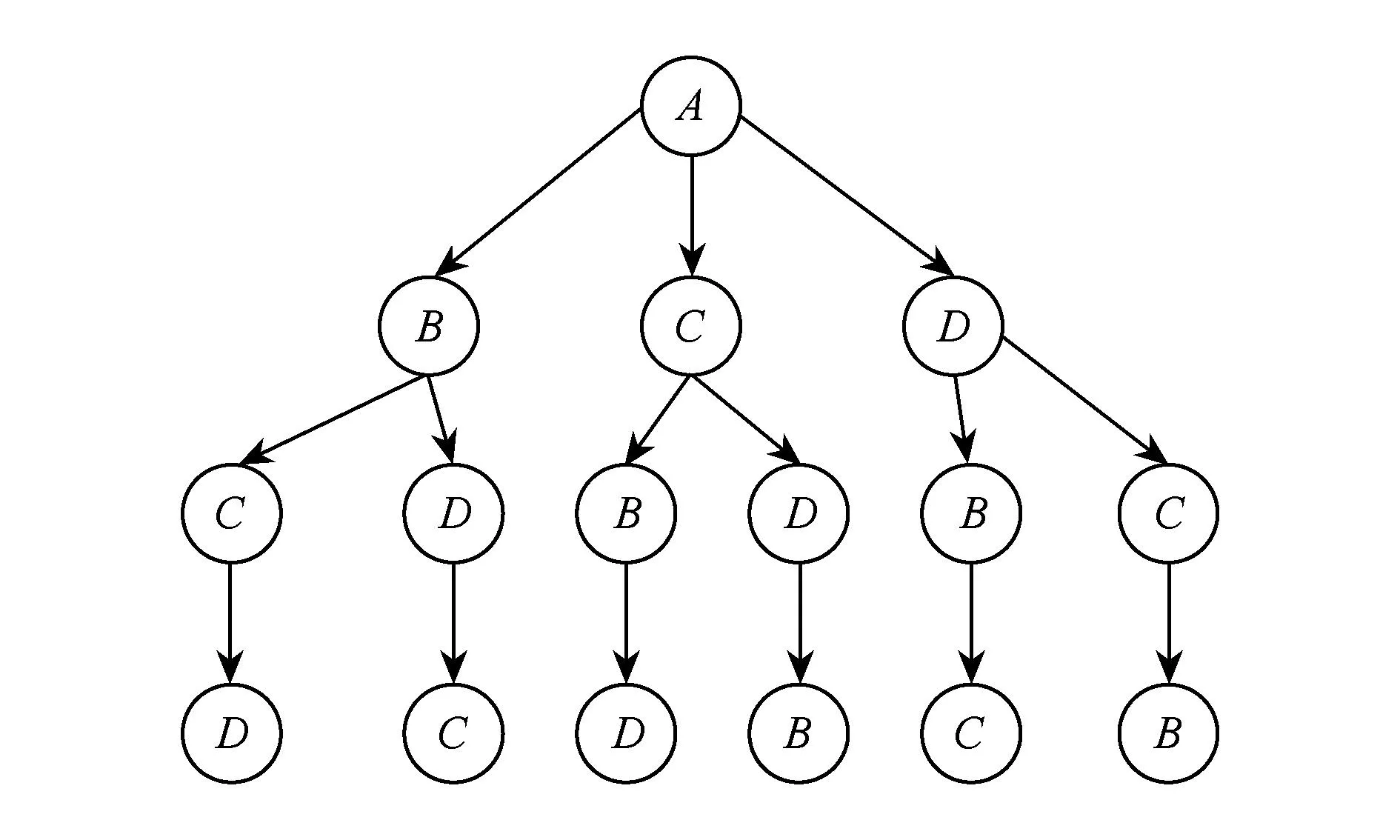
Fig. 1　Permutation tree started by A.图1　以A开始的排列所构成的树

遍历路径上重复的节点就代表到该点的部分聚类结果可以在计算对应数据时复用.例如，对于ABCD和ABDC两种排列表示的数据集，它们可以复用的部分就是AB上各点的局部聚类结果.以A开始的排列中所有需要计算的划分个数就是图1中节点的个数，以B，C，D开始的排列也类似.可以计算出当p=4时需要计算的划分数是64(即16×4).按4个划分组成一个数据集来计算的话，等同于16份数据集的计算量.与不复用时(p=4时，需要计算4!=24个数据集)相比，计算量只有原来的23，随着p的增大，复用的程度会增加.可以归纳出采用复用技术时，需要计算的等量数据集个数为

(5)

不采用复用技术时，需要计算的数据集的个数为p!，复用与不复用时计算量的比值为

(6)

当p分别为2，3，4，5，6时，如果尽量复用，则需要计算的数据集个数分别为2，5，16，65，326；如果完全不复用，则需要计算的数据集为2，6，24，120，720，两者比例为1，0.833，0.667，0.542，0.453.由式(6)可知，当p=2时不可以复用，当p增大时复用的程度会增大.

由以上分析可知，采用复用技术与不采用复用相比，能较大程度地减小计算量、提高聚类的速度.

2.4算法实现

根据2.1～2.3节的设计，下面给出p-CLOPE算法.

算法2.p-CLOPE算法.

① 划分数据文件成p片；

② 变换p片数据之间的顺序得p!个数据集{D1,D2,…,Dp!};

③ forDk∈{D1,D2,…,Dp!}

④ while 未到文件Dk的尾部

⑤ 读下一条交易〈t,unknown〉；

⑥ 将t放入一个使收益最大的现有簇或新簇Ci中;

⑦ 将〈t,i〉写回数据集；

⑧ endfor

⑨ 选择具有最大收益的Dm.

⑩ repeat

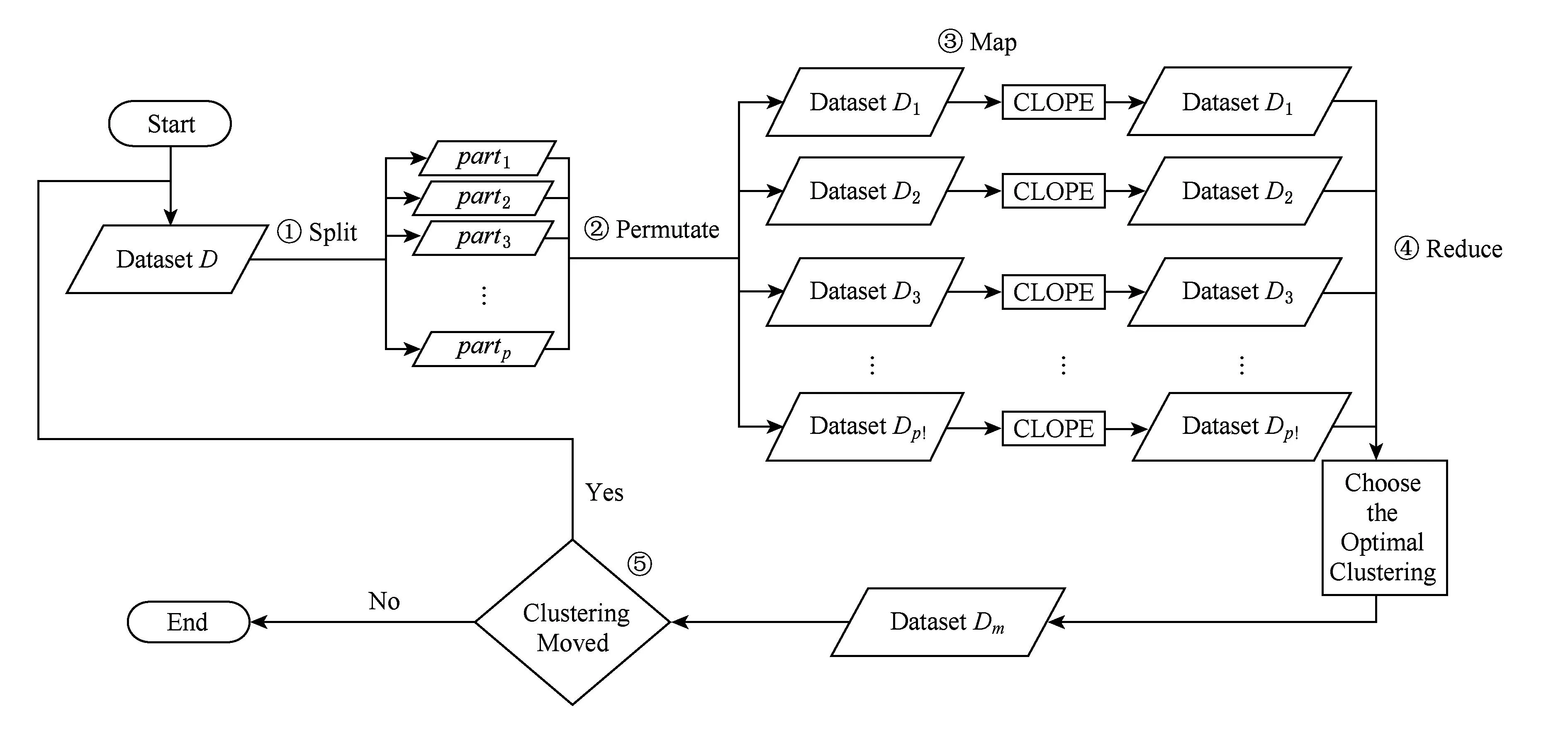
Fig. 2　Execution flow chart of p -CLOPE.图2　p -CLOPE的执行流程图

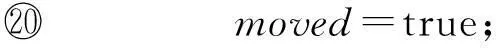
2.5并行实现

p-CLOPE算法的每一轮迭代都先将输入数据集划分成p等份，然后排列成p!份新的数据集，分别对这些数据集聚类，再将该轮迭代的最优聚类结果作为下一轮迭代的输入，反复迭代，直至得到最优的聚类划分.在每一轮迭代中，由于对每一份数据集Di都要单独执行一系列运算，计算出一个聚类划分，再比较对应的聚类划分根据式(3)计算的收益值，找出收益值最大的聚类.因此我们将每一份数据集Di的计算放在不同的计算单元上独立完成，而比较全局收益值的计算可以统一在一个计算单元上处理.这一过程完全可以先并行运算再全局比较大小，这为并行聚类的实现提供了可能性.

MapReduce是一种数据并行编程模型[11]，但它同时又能实现一定程度的共享变量和消息传递，因此与其他的并行计算模型(如MPI[12]，OpenMP[13]等)相比较，MapReduce具有非常大的优势.用MapReduce编程模型实现p-CLOPE算法的编程方法是：对不同数据集Di的聚类用不同的Map来完成，比较全局收益值用Reduce来完成.

我们在分布式基础架构Hadoop[11,14]上实现了p-CLOPE算法，使用HDFS存储数据，使用Map -Reduce实现算法并行化.具体来说，首先将待聚类的数据集D以指定的文本格式上传到HDFS，作为程序的输入文件.根据输入文件的大小将D划分成p等份，再将这p等份数据块排列生成p!份数据集{D1,D2,…,Dp!}.将每一份数据集Di分发到一个Map任务进行一次迭代的聚类操作，并将得到的聚类划分以及根据式(3)计算得到的收益值等中间结果写回HDFS.所有的Map任务结束后，通过一次Reduce过程，比较p!份数据集的聚类收益值，选出收益值最大的聚类结果数据集作为下一轮迭代的输入.依此迭代，当最优的聚类中所有的交易都没有移动时，聚类过程结束.这样得到的聚类划分就是整个算法所要求的最优聚类结果.执行流程如图2所示:

2.6时间与空间复杂度

CLOPE算法一次迭代的时间复杂度是O(N×K×A)，其中A是每条交易的平均长度，N是交易的条数，K是簇的个数[7].它的空间复杂度是O(M×K)，其中M是维度，K是簇的个数.比如，对拥有10 000个维度和1 000个簇的数据集使用的内存为40 MB[7]，由此可看出CLOPE算法具有非常快的执行速度而且非常省内存.p-CLOPE算法由于一次迭代需要计算p!份数据集，在单机单线程上运行时，采用每排列生成一份数据集就执行一次的方式，p-CLOPE的一次迭代的时间复杂度是CLOPE算法一次迭代的p!倍，即为O(p!×N×K×A)，空间复杂度同CLOPE算法相当，但是由于p-CLOPE每次迭代后都选出最好的聚类结果，通常会比CLOPE算法在更少的迭代次数后就收敛了(即聚类结束).

在处理少量数据时，网络通信代价比数据处理的计算代价大很多，运行在分布式平台Hadoop上的p-CLOPE算法并没有优势，甚至不如串行p-CLOPE.但是在处理大量数据时，并行p-CLOPE所花费的时间比串行p-CLOPE大大缩短，使用HDFS又能很好地实现大规模数据的存储.

2.7加速比分析

加速比[15]是串行运行时间与并行运行时间的比率.p-CLOPE算法在每一轮的迭代中，串行时要依次处理p!份数据集，并行处理时这p!份数据集同时被处理，在Hadoop集群中每个任务处理一份数据集.

在定量分析加速比之前先简单介绍Hadoop集群中的任务执行机制.Hadoop(版本：1.xx系列)集群是MasterSlave架构，包含一台Master服务器和若干台Slave服务器.Master服务器上运行的进程有NameNode，SecondaryNameNode和JobTracker；Slave服务器上运行的进程有DataNode和TaskTracker.TaskTracker需要设置(每个节点上)可运行的任务数的上限(默认是4).2类服务器上运行的进程也代表着它们的功能角色.JobTracker向TaskTracker下达启动任务命令后，TaskTracker会为每个任务创建一个单独的Java虚拟机(这是为了防止任务之间的干扰)，并有专门的线程监控其资源的使用情况[16].

目前，计算机的CPU一般都是多核多线程(例如，Intel i7 CPU是4核8线程)，内存也较大.我们假设每个TaskTracker上设置的任务数为T时，一个TaskTracker管理的所有任务不是以时间分片的方式交替使用CPU，而是拥有足够的CPU和内存等计算资源来并行执行，此时所有的TaskTracker管理的所有任务也都可以并行执行.如果集群中共有N台TaskTracker，那么整个集群能够运行的任务总数Total_Task如式(7)所示：

Total_Task=T×N.

(7)

当p!≤Total_Task时，所有的p!份数据集都可以并行计算，这时整个p-CLOPE算法可以完全并行运行，其加速比的理想值为p!.

当p!>Total_Task时，所有的p!份数据集不可能并行计算，必然会有先后之分.Hadoop集群会分批执行任务，每批的任务数为Total_Task，所以分的批数B如式(8)所示：

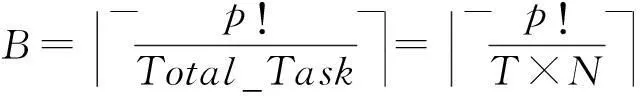
(8)

可以推导出此时理想的加速比如式(9)所示：

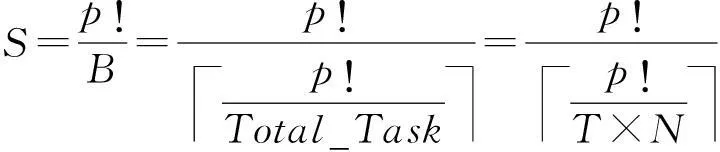
(9)

从式(9)不难得出加速比的上限值是Total_Task.

当处理大量数据时，并行p-CLOPE具有显著的优势.但如果此时集群的CPU和内存等计算资源相对不够，或者每个TaskTracker设置的任务数过大时，都会导致任务不能拥有足够的CPU和内存等计算资源来并行运行，进而不能达到理想的加速比.集群环境受到网络和IO开销的影响时，也不能达到理想的加速比.

对理想的加速比举例说明如下：如果集群中的任务数为8，每个TaskTracker上设置的任务数为4时(CPU、内存等计算资源足够)，8个任务可以完全并行，这时整个集群中能同时运行的最多任务数为32.在这种环境的集群上用p-CLOPE算法对某个数据集进行聚类，当p=4时，p!=24，24<32，p-CLOPE算法可以完全并行，理想的加速比为24；当p=5时，p!=120，120>32，p-CLOPE算法不能完全并行，由式(9)计算得到理想的加速比为30；当p=6时，同理可以计算出理想的加速比为31.3.

3实验与分析

由于本文最大的贡献在于提出的p-CLOPE算法对CLOPE算法聚类质量进行了提升，其次在于将p-CLOPE算法并行化，所以实验主要对比p-CLOPE算法和CLOPE算法的聚类质量.

这里采用CLOPE

算法提出的全局评估函数(见式(3))作为评价聚类结果的指标.全局收益值Profitr(C)越大，聚类划分越优.实验采用了3组数据集：组1是CLOPE算法测过的蘑菇数据集，属性项数固定；组2是植物数据集，其属性项数是不定的；组3是美国人口普查数据集，其属性项数也是固定的.在组3百万条数据级别的情况下，我们不仅比较了p-CLOPE与CLOPE的聚类质量，还比较了CLOPE、串行p-CLOPE、并行p-CLOPE三者的执行时间.

实验所使用的CLOPE算法的实现程序来自于数据挖掘软件Weka[17]中的版本(在实验中标记为Weka-CLOPE)和我们实现的版本(在实验中标记为CLOPE)，因为Weka软件中实现的CLOPE算法实际上只用到了原CLOPE算法的初始化阶段，并没有完全按照文献[7]提出的CLOPE算法来实现，而我们实现的CLOPE算法是完全按文献[7]来实现的.实验所用p-CLOPE算法有串行实现和在Hadoop上并行实现2个版本.Weka-CLOPE、CLOPE、串行p-CLOPE是在单机(8 GB的内存、i7处理器的联想PC机)上执行的，并行p-CLOPE是在9台这样的机器搭建的Hadoop集群上执行的.

3.1蘑菇数据集

蘑菇数据集(Mushroom)来自加州大学欧文分校机器学习库①(UCI machine learning repository)，它被很多算法测试过[5]，也是原CLOPE算法测试过的数据集,该数据集有8 124条交易，每条交易有22个属性，分可食用(edible)和有毒的(poisonous)2个类别，各有4 208和3 916条交易.所有的属性项共有116个不同的值，2 480个缺失属性值用问题号“?”表示.

以下分别用Weka-CLOPE，CLOPE，p-CLOPE进行聚类，用收益值Profitr(C)作为衡量聚类质量的指标进行测试.进行比较时以CLOPE算法的收益值为基准线，Weka-CLOPE，p-CLOPE算法的收益值与之相比较.对p-CLOPE算法测试了参数p取不同值时的情况，每组对应的算法用p-CLOPEp来表示，用排斥因子作为X轴、用收益比值作为Y轴，实验结果如图3所示.

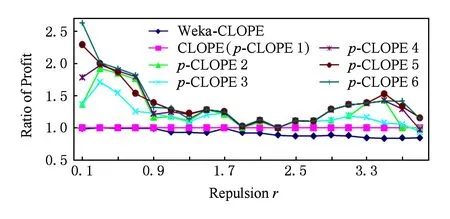
Fig. 3　Clustering results on Mushroom datasets.图3　蘑菇数据集的实验对比图

实验中排斥因子r取0.1～3.9，以0.2为步长；参数p取1～6，以1为步长.图3中收益值比率为1的是CLOPE算法，以其作为基准线，Weka-CLOPE在CLOPE之下，p-CLOPE在CLOPE之上.因为Weka-CLOPE只实现了CLOPE算法的初始化阶段，没有继续迭代以寻找更好的聚类结果，这样做虽然节约了时间，但毕竟损失了精度，所以结果自然会差于CLOPE.p-CLOPE需要同时处理p!份数据集，由于p!增长太快，所以在实验中p值最大只取到了6，这时并行计算的任务数为720个.当p=1时，p-CLOPE算法退化为CLOPE算法.从图3中还可以看出，在排斥因子r一定时，随着参数p的增大，p-CLOPE的收益值一般是越来越大，但是会存在一个上限，图3中p-CLOPE取不同参数时曲线有一定程度的重合正好直观地说明了这一点.

对大多数实际的数据集，r>1才有意义，否则2条没有相同属性项的交易会被放入同一个簇[7].在介绍CLOPE算法的文献[7]中，当r=3.1时取得最好的聚类结果，而在我们的实验中p-CLOPE 4在相同的r=3.1时取得了比CLOPE高35.7%的收益值.

3.2植物数据集

植物数据集(Plants)同样来自加州大学欧文分校机器学习库，是从美国农业部的植物数据库②中提取出来的，其中包含所有的植物种类以及每种植物在美国和加拿大的哪些州出现过的信息.总共的交易条数为34 781，每条交易由植物的拉丁名和出现过的州名的缩写组成，这些州名可以看作是交易的属性项，不超过70个.与蘑菇数据集的数据属性项相比，植物数据集的每条交易的属性项个数不一定相同(因为有的植物只在部分州出现)，而且属性项的位置也是任意的，与出现的顺序无关.

分别用Weka-CLOPE，CLOPE，p-CLOPE进行聚类，实验结果如图4所示.

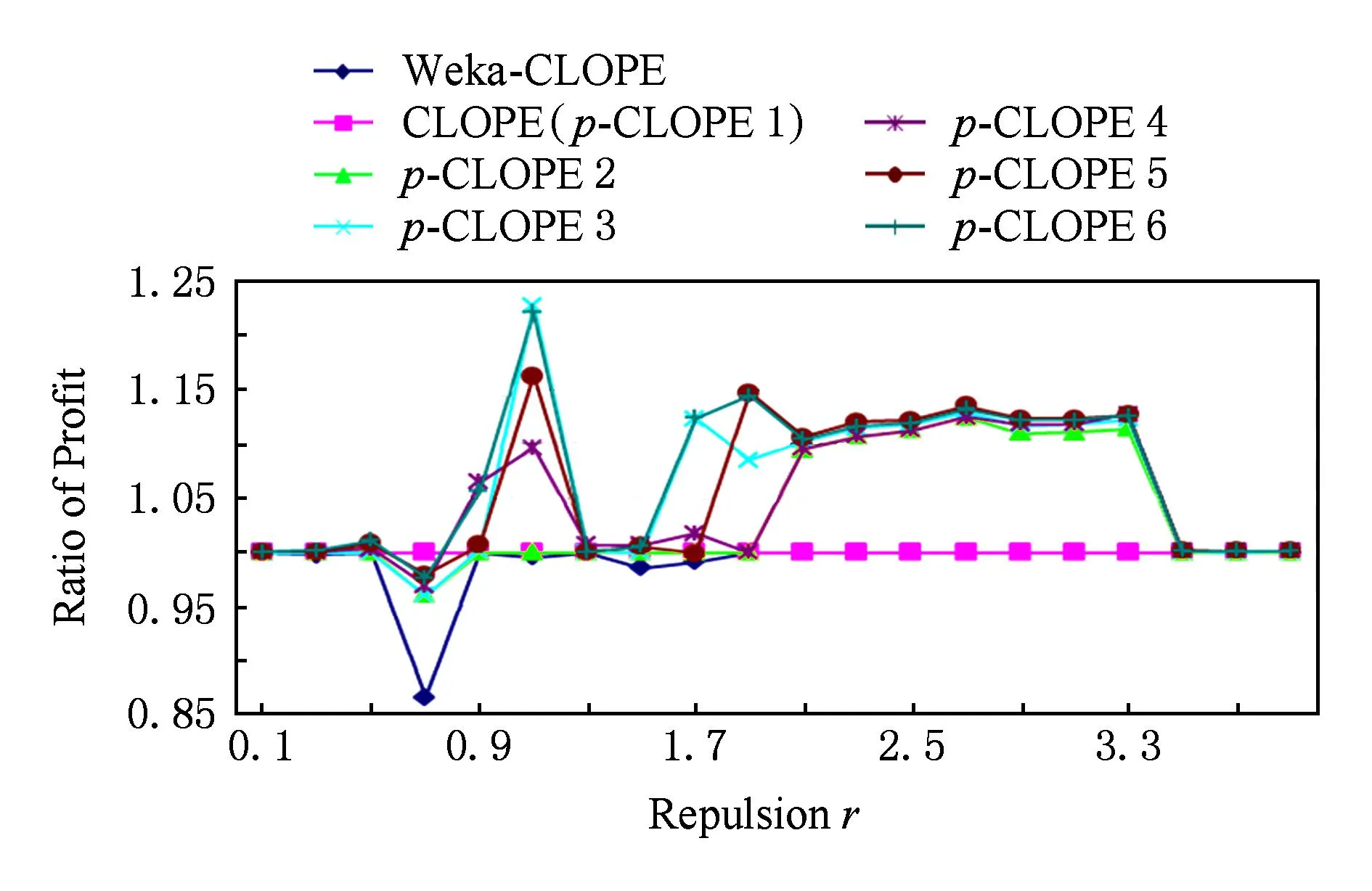
Fig. 4　Clustering results on Plants datasets.图4　植物数据集的实验对比图

从图4可以看出，在绝大多数情况下，p-CLOPE算法的聚类质量相比CLOPE算法有较大提升.

3.3美国人口普查数据集

美国人口普查数据集(US Census data set)同样来自加州大学欧文分校机器学习库，是从美国商务部人口普查局①获取的，具体是从1990年美国人口普查全样本数据中按1%的比例抽取的公共使用微数据样本.总共交易条数为2 458 285，包括祖先、族群、拉美族裔来源、行业职业、语言、出生地等领域的68个属性.与前2个数据集相比，这个数据集的交易条数达到百万级别.

分别用Weka-CLOPE，CLOPE，p-CLOPE进行聚类，实验结果如图5所示：

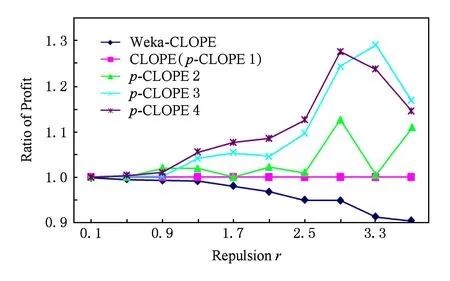
Fig. 5　Clustering results on US Census datasets.图5　美国人口普查数据集的实验对比图

从图5可以看出，p-CLOPE算法的聚类质量相比CLOPE算法都有提升，特别是当排斥因子取较大值时(这也是实际有意义的情况)，质量有明显的提升.

对这组百万级的数据集，我们还比较了CLOPE、串行p-CLOPE、并行p-CLOPE三者的执行时间.3个算法在划分参数p=4时的执行时间如图6所示：

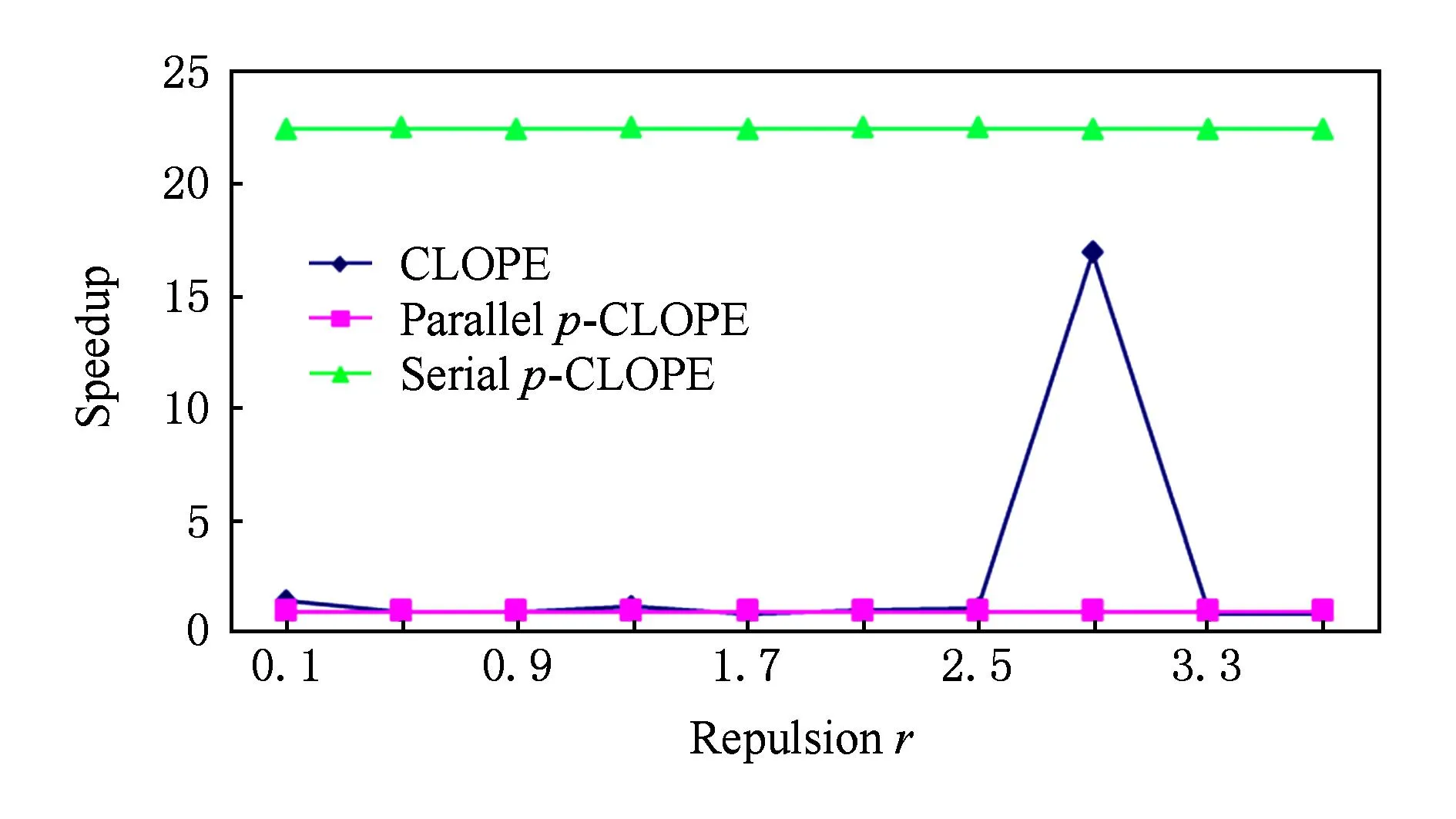
Fig. 6　The execution time of three algorithms.图6　3个算法的执行时间对比图

从图6可以看出，在大部分情况下，并行p-CLOPE算法的执行时间比CLOPE算法短.原因在于虽然使用MapReduce并行方式实现时，p-CLOPE算法会有一定的网络通信开销，但是它会更快地收敛到最优结果，因此迭代次数一般会比CLOPE算法少，这样总的时间也会更短.并行p-CLOPE与串行p-CLOPE相比，执行时间有大幅减少，从实验数据计算得出的平均加速比为22.4.对本实验中并行p-CLOPE算法的加速比分析如下：本实验使用的Hadoop集群由9台计算机组成，其中8台计算机作为DataNode，每个TaskTracker的任务(task)数为4，所以整个集群可同时运行的任务数为32.由于每台计算机的CPU配置都是4核8线程，内存配置为8 GB，集群中的每个任务可以获得超过1 GB的内存和足够的CPU资源.美国人口普查数据集的大小为345 MB(由2.6节的分析知，p-CLOPE算法非常节省内存，实际上还不需要把整个数据集全部放入内存)，所以集群的32个任务能够获得足够的CPU和内存等计算资源来并行执行.本次实验中p=4，p-CLOPE算法的每一次迭代中需要同时处理24份数据集，24<32.在这种情况下，这24份数据集完全可以并行处理，即p-CLOPE算法在当前情况下可以完全并行化，所以本次实验获得的加速比为22.4,接近p!，这与本文2.7节的理论分析是一致的.

4结论

本文深入研究了基于统计直方图思想的分类数据聚类算法CLOPE，指出了该算法由于受输入交易顺序的影响而不能获得最优聚类划分的问题.针对此缺陷，我们提出了一种基于等分划分再排列思想的p-CLOPE算法进行改进.实验表明，p-CLOPE算法能比CLOPE算法取得更优的聚类结果.对蘑菇数据集在CLOPE算法取得最优聚类结果时，p-CLOPE取得比CLOPE高35.7%的收益值.对大量数据集p-CLOPE算法也取得了比CLOPE算法更好的聚类质量，同时并行p-CLOPE比串行p-CLOPE极大地缩短了聚类时间，取得了很好的加速比.我们在Hadoop平台上用MapReduce并行编模型实现了一个包含p-CLOPE相关算法的聚类工具，已发布到开源社区①.

下一步的研究工作将结合权重对不同属性项的影响继续改进p-CLOPE算法，同时研究输入交易的顺序对其他聚类算法的影响.

参考文献

[1]Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496

[2]Agresti A. Categorical Data Analysis[M]. New York: John Wiley & Sons, 2014

[3]Huang Z. A fast clustering algorithm to cluster very large categorical data sets in data mining[C]Proc of Workshop on Research Issues on Data Mining and Knowledge Discovery. New York: ACM, 1997

[4]Macqueen J. Some methods for classification and analysis of multivariate observations[C]Proc of the 5th Berkeley Symp on Mathematical Statistics and Probability. Berkeley, CA: University of California Press, 1967: 281-297

[5]Guha S, Rastogi R, Shim K. ROCK: A robust clustering algorithm for categorical attributes[C]Proc of the 15th Int Conf on Data Engineering (ICDE 1999). Los Alamitos, CA: IEEE Comuter Society, 1999: 512-521

[6]Wang K, Xu C, Liu B. Clustering transactions using large items[C]Proc of the 8th Int Conf on Information and Knowledge Management. New York: ACM, 1999: 483-490

[7]Yang Y, Guan X, You J. CLOPE: A fast and effective clustering algorithm for transactional data[C]Proc of the 8th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2002: 682-687

[8]Ong K L, Li W, Ng W K, et al. SCLOPE: An algorithm for clustering data streams of categorical attributes[G]LNCS 3181: Proc of the 6th Int Conf on Data Warehousing and Knowledge Discovery. Berlin: Springer, 2004: 209-218

[9]Yap P H, Ong K L.σ-SCLOPE: Clustering categorical streams using attribute selection[G]LNCS 3682: Proc of the 9th Int Conf on Knowledge-Based Intelligent Information and Engineering Systems, Part Ⅱ. Berlin: Springer, 2005: 929-935

[10]Li Jie, Gao Xinbo, Jiao Licheng. Fuzzy CLOPE algorithm and its parameter optimal choice[J]. Control and Decision, 2004, 19(11): 1250-1254 (in Chinese)(李洁, 高新波, 焦李成. 模糊 CLOPE 算法及其参数优选[J]. 控制与决策, 2004, 19(11): 1250-1254)

[11]Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113

[12]Pacheco P S. Parallel Programming with MPI[M]. San Francisco, CA: Morgan Kaufmann, 1997

[13]Dagum L, Menon R. OpenMP: An industry standard API for shared-memory programming[J]. IEEE Computational Science & Engineering, 1998, 5(1): 46-55

[14]Shvachko K, Kuang H, Radia S, et al. The Hadoop distributed file system[C]Proc of the 26th IEEE Symp on Mass Storage Systems and Technologies (MSST). Piscataway, NJ: IEEE, 2010: 1-10

[15]Eager D L, Zahorjan J, Lazowska E D. Speedup versus efficiency in parallel systems[J]. IEEE Trans on Computers, 1989, 38(3): 408-423

[16]Dong Xicheng. Hadoop Internals: In-Depth Study of MapReduce[M]. Beijing: China Machine Press, 2013 (in Chinese)(董西成. Hadoop技术内幕:深入解析MapReduce架构设计与实现原理[M]. 北京: 机械工业出版社, 2013)

[17]Hall M, Frank E, Holmes G, et al. The WEKA data mining software: An update[J]. ACM SIGKDD Explorations Newsletter, 2009, 11(1): 10-18

Ding Xiangwu, born in 1963. PhD and associate professor. Member of China Computer Federation. His main research interests include database, column-stores, distributed processing, etc.

Guo Tao, born in 1988. Master. His research interests include big data and data mining (j2cms.org@gmail.com).

Wang Mei, born in 1980. PhD and professor. Her primary research interests include database, image semantic analysis, and information retrieval (wangmei@dhu.edu.cn).

Jin Ran, born in 1978. Associate professor, received PhD degree from College of Information Science and Technology, Donghua University in 2015. His main research interests include artificial intelli-gence, wire less sensor network, cloud com-puting and data mining (ran.jin@163.com).

A Clustering Algorithm for Large -Scale Categorical Data and Its Parallel Implementation

Ding Xiangwu1, Guo Tao1, Wang Mei1, and Jin Ran2

1(CollegeofComputerScienceandTechnology,DonghuaUniversity,Shanghai201620)2(FacultyofComputerScienceandInformationTechnology,ZhejingWanliUniversity,Ningbo,Zhejiang315100)

AbstractCLOPE algorithm has achieved good results in clustering large, sparse categorical datasets with high dimensions. However, it is hard to stably find the global optimal clusters since the data order can affect the result of clustering. To deal with this problem, this paper proposes p -CLOPE algorithm iteratively dividing input data into multiply equal parts and then clustering their different permutations. In each iteration of p -CLOPE algorithm, the input dataset is split into p parts and they are permuted into p! datasets with different part orders, then each dataset is clustered and the optimal clustering is chosen according to the profit as the input of next iterations. In order to handle time complexity of the process, a result reusing strategy is put forward that can improve the speed of clustering, further. Finaly, a distributed solution is put forward that implements p -CLOPE on Hadoop platform and a clustering tool is developed which has been released to the open source community. Experiments show that p -CLOPE can achieve better results than CLOPE. For the Mushroom dataset, when CLOPE achieves optimal results, p -CLOPE can achieve 35.7% higher profit value than CLOPE. When dealing with big data, parallel p -CLOPE greatly shortens the computing time compared with serial p -CLOPE, and it achieves nearly p! speedup when there is enough computing resource.

Key wordscategorical data; CLOPE; p -CLOPE; parallel clustering; MapReduce

收稿日期：2014-12-23；修回日期：2015-04-08

基金项目：国家自然科学基金项目(61103046)；上海市自然科学基金项目(11ZR1401200)

中图法分类号TP312

This work was supported by the National Natural Science Foundation of China (61103046) and the Natural Science Foundation of Shanghai (11ZR1401200).