一种基于最大值损失函数的快速偏标记学习算法
周 瑜 贺建军, 顾 宏 张俊星
1(大连理工大学电子信息与电气工程学部 辽宁大连 116024)2(大连民族大学信息与通信工程学院 辽宁大连 116600)(yuzhou829@sina.com)
一种基于最大值损失函数的快速偏标记学习算法
周瑜1贺建军1,2顾宏1张俊星2
1(大连理工大学电子信息与电气工程学部辽宁大连116024)2(大连民族大学信息与通信工程学院辽宁大连116600)(yuzhou829@sina.com)
摘要在弱监督信息条件下进行学习已成为大数据时代机器学习领域的研究热点,偏标记学习是最近提出的一种重要的弱监督学习框架,主要解决在只知道训练样本的真实标记属于某个候选标记集合的情况下如何进行学习的问题,在很多领域都具有广泛应用.最大值损失函数可以很好地描述偏标记学习中的样本与候选标记间的关系,但是由于建立的模型通常是一个难以求解的非光滑函数,目前还没有建立基于该损失函数的偏标记学习算法.此外,已有的偏标记学习算法都只能处理样本规模比较小的问题,还没看到面向大数据的算法.针对以上2个问题,先利用凝聚函数逼近最大值损失函数中的max(·)将模型的目标函数转换为一个光滑的凹函数,然后利用随机拟牛顿法对其进行求解,最终实现了一种基于最大值损失函数的快速偏标记学习算法.仿真实验结果表明,此算法不仅要比基于均值损失函数的传统算法取得更好的分类精度,运行速度上也远远快于这些算法,处理样本规模达到百万级的问题只需要几分钟.
关键词偏标记学习;最大值损失函数;凝聚函数;弱监督学习;分类精度
在传统分类技术中,通常需要通过一个样本的真实标记信息准确给定的训练样本集来训练分类器,而在很多实际问题中,准确确定样本的真实标记信息是很困难或者需要付出很大代价的.例如在医疗诊断中,医生通过一个病人的症状(如关节疼、发烧、血沉高),往往可以判断他得了哪几种疾病(可能是风湿性关节炎或布氏杆菌病),而很难确定具体是哪种疾病,在利用传统分类技术构造疾病诊断的预测算法时,这类数据需要被排除在外,而其实这类数据对于缩小疾病的可能范围往往是非常重要的;再如,在利用众筹的方式标注训练数据时,由于标注人员个人素质的差异,标注的结果往往会不一致,在传统的分类算法中,这种不一致的数据往往会被舍弃,其实,虽然标注结果不一致,但是也已经缩小了类别的可能范围,所以这类数据也是有用的.偏标记集学习(partial label learning[1-3],也称learning from candidate labeling sets[4]ambiguous label learning[5],superset label learning[6]),就是研究这类数据(即不能准确确定训练样本的真实标记而只知道它属于类别标记集合的某一子集)的分类问题的一种新机器学习框架.由于偏标记学习是对传统分类技术的一个扩展,放松了构造训练集的条件,因此它与传统分类技术一样具有广阔的应用空间,可以解决图像处理[7]、文本挖掘[8]、医疗诊断[9]等领域的各种实际问题.

1模型建立
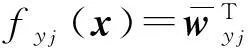
(1)
p(Yi|xi,W)=
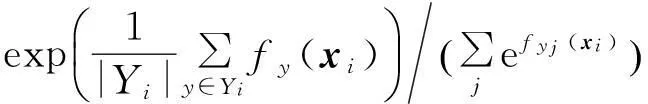
(2)
可以看出,以上2个似然函数都假设样本xi的候选标记集Yi中的每个标记都对似然函数p(Yi|xi,W)具有一样的贡献,这将导致最大化p(Yi|xi,W)时,与Yi中的各个元素对应的潜变量同时取得最大值,因此这2个似然函数本质是假定了Yi的所有元素都是xi的真实标记,这与偏标记学习框架描述的“样本的候选标记中有且只有一个标记是样本的真实标记”的概念是不一致的.本文将定义一种新的似然函数:
(3)
该似然函数本质上把是真实标记的概率最大的候选标记作为样本的真实标记.由于概率模型中似然函数与参数模型中的损失函数本质上是一样的,而文献[2]的理论分析表明,最大值损失较均值损失更符合偏标记学习的实际情况,因此由式(3)定义的似然函数也要优于由式(1)(2)定义的似然函数.
(4)
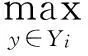
凝聚函数(aggregate function)
(5)
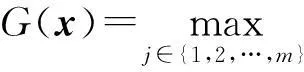

(6)
因此,对于有限正整数m,当l→+∞时,Gl(x)能单调一致地逼近G(x).根据式(6)描述的关系,我们可以得到2个关系式:
(7)
(8)
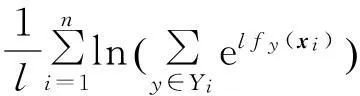
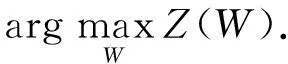
(9)
显然,新目标函数Z(W)不仅可以一致地逼近式(4),而且还是一个光滑函数.

(10)
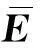
(11)
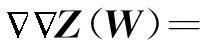
(12)
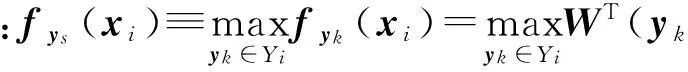

(13)
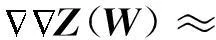
(14)
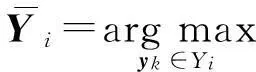
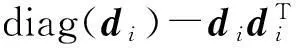

2模型求解
由于目标函数Z(W)是一个凹函数,因此很多常用的优化方法都可以用来求其最大值点.本文将建立2种模型求解方法,对于样本规模比较小的问题采用阻尼牛顿法来求解,对于样本规模比较大的问题将利用随机拟牛顿法来建立一种快速求解方法.
2.1阻尼牛顿法
阻尼牛顿法的迭代公式如下:

(15)

2.2随机拟牛顿法
为了处理大数据问题,本文拟采用文献[17]提出的随机拟牛顿法来建立一种快速模型求解方法.为了便于描述,我们将式(9)(10)描述的最大值问题变换为最小值问题来求解:

(16)
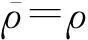

(17)

(18)
(19)
(20)
其中,S,SH为随机选取的训练数据集D的子集.
随机拟牛顿法[17]的迭代为

(21)
其中,αk为步长,αk的选取会对算法的收敛速度有一定的影响,本文采用与文献[17]一样的定义方式,即αk=βk(β为事先给定的常数);Ht为海森矩阵的近似矩阵,通过与有限储存拟牛顿方法(limited-memory Broyden-Fletcher-Goldfarb-Shanno Broyden, L-BFGS)[18]中一样的方法来求得.算法1、算法2给出了随机拟牛顿法的算法流程图,关于该方法的详细描述见文献[17].
算法1. 随机拟牛顿法的算法流程.
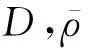
输出: W.
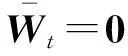
② fork=1,2,…,K-1

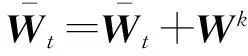
⑤ ifk≤2L

⑦ else
⑧ 根据算法2计算Ht;

⑩ end if







算法2. 海森矩阵Ht的计算流程.
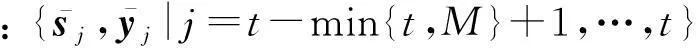
输出: Ht.

② forj=t-min{t,M}+1,…,t
③ 计算ρj=1;
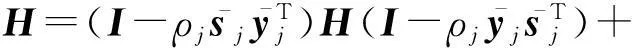
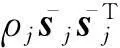
⑤ end for;
⑥ Ht=H.
3仿真实验
本文的主要创新在于使用了最大值似然函数和建立了面向大数据问题的快速偏标记学习算法,因此,下面将分别从这2个方面验证所建算法的性能.为了便于区分,在下面的仿真实验中我们用PLLOG-Max表示本文建立的基于最大值似然函数的偏标记学习算法,PLLOG-Max-DN表示基于阻尼牛顿法求解的算法,PLLOG-Max-SQN表示基于随机拟牛顿法求解的算法.
3.1验证最大值似然函数对算法性能的影响
为了验证最大值似然函数对算法性能的影响,我们先将PLLOG-Max-DN算法与CLPL算法[2]以及使用由式(1)(2)定义的2种均值似然函数所建立的算法(分别简记为PLLOG-Naive,PLLOG-Average算法)进行了比较.对于PLLOG-Average算法,也是采用阻尼牛顿法对模型进行求解的;对于PLLOG-Naive算法,由于目标函数不是一个凸(或凹)函数,因此采用文献[19]提出的CCCP算法对其进行求解,这2个算法的其他推导过程都是与PLLOG-Max-DN算法一样的.PLLOG-Max-DN,PLLOG-Naive,PLLOG-Average算法都只有一个需要给定的模型参数,即正则化项的系数ρ,在本节的仿真实验中,ρ是通过在训练集上利用3折交叉验证法选取得到的,CLPL算法的所有参数都是按照文献[2]的建议设置的.我们在5个UCI数据集[20]和2个真实偏标记学习数据集[3]上对这4个算法进行了比较,这7个数据集的详细信息如表1所示:
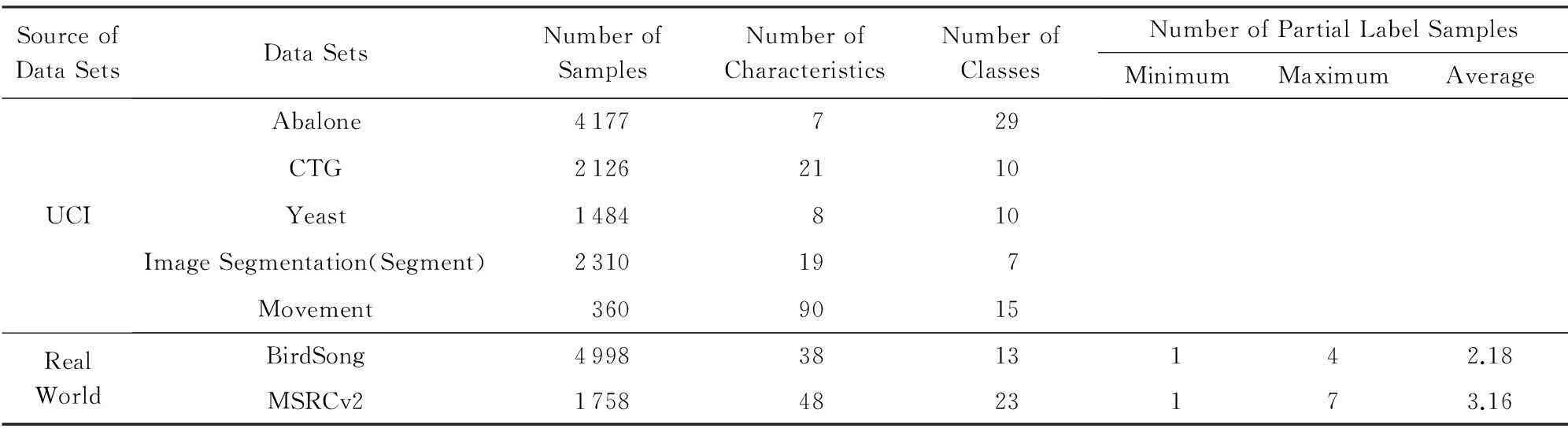
Table 1 The Data Sets for Validating the Performance of Max-likelihood Based Algorithm
由于UCI数据集是标准的传统分类数据集,我们采用了2个控制参数p,r来把它们变换为了偏标记数据集,其中p表示偏标记样本(即|Yi|>1)在整个样本集中的比例,r表示偏标记样本的除真实标记以外的候选标记个数,即r=|Yi|-1.变换过程如下:对于给定的每一对参数(p,r),先从原始的UCI数据集中随机选取pn个样本(n为样本总数),然后对于每一个被选取的样本,随机地从它的真实标记以外的类别标记中选取r个与真实标记一起构成该样本的候选标记.表2给出了4个算法在由不同的控制参数(p,r)生成的数据集上的预测精度,每个数据集上的结果都是5次10折交叉验证的平均结果.表2中黑体显示的是PLLOG-Max-DN,PLLOG-Naive,PLLOG-Average三个算法中最好的结果,下划线表示的是PLLOG-Max-DN算法和CLPL算法之间相比最好的结果.可以看出,就PLLOG-Max-DN,PLLOG-Naive,PLLOG-Average三个算法相比,PLLOG-Max-DN算法在生成的45个控制数据集中的33个上取得了最好的结果,PLLOG-Naive算法在10个数据集上取得了最好结果,而PLLOG-Average算法只在2个数据集上取得了最好结果,而且对于那些没有取得最好结果的数据集,PLLOG-Max-DN算法的结果也基本与最好结果相差很少,这就表明最大值似然函数要优于其他2种均值似然函数;而PLLOG-Max-DN和CLPL算法相比,PLLOG-Max-DN算法在45个控制数据集中的29个上取得了最好的结果,CLPL算法在16个上取得了最好结果,而且其中在6个上是以微弱的优势胜出,因此PLLOG-Max-DN算法要优于CLPL算法.
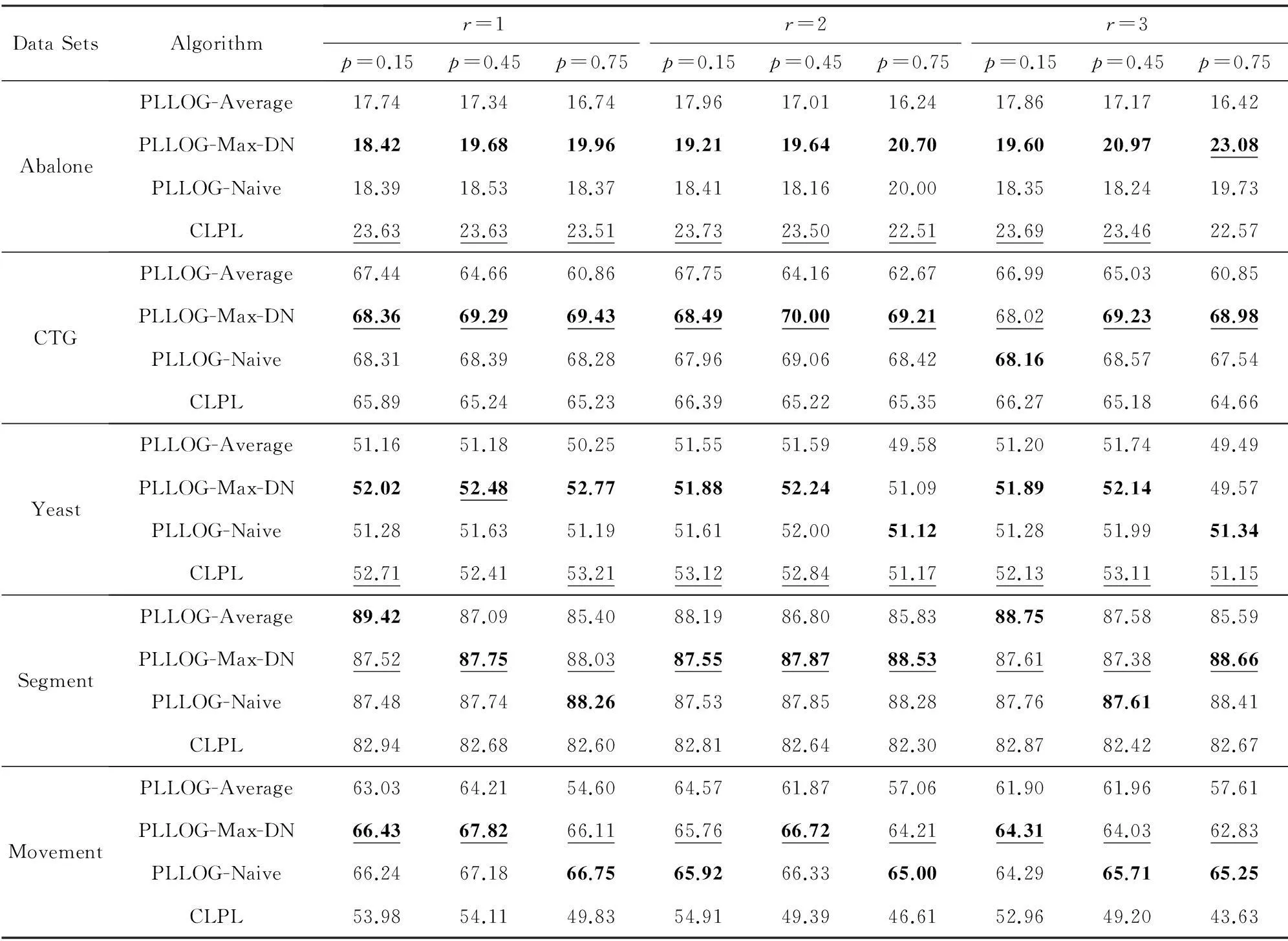
Table 2 The Accuracy of Each Algorithm on the UCI Data Sets
表3给出了4个算法在2个真实数据集上的预测精度,遗憾的是PLLOG-Max-DN算法只在一个数据集上取得了最好的结果,主要原因是BirdSong数据集是从一个多标记学习问题中采集的,可能BirdSong数据集中的一部分样本的候选标记本身都是样本的真实标记,从而影响了算法的性能.
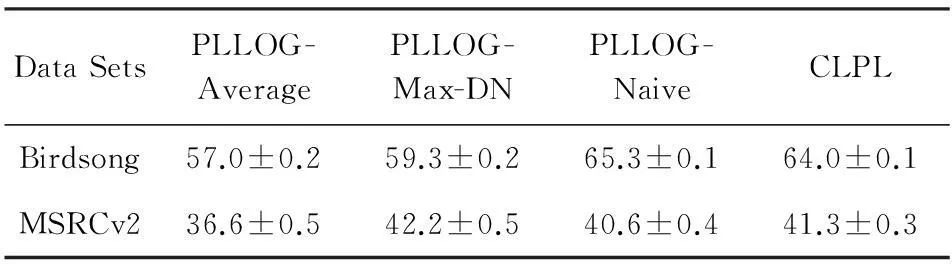
Table 3 The Accuracy of Each Algorithm on the Real-world
3.2验证快速模型求解算法的性能
本节将在5个规模比较大的UCI数据集上对本文建立的快速偏标记学习算法PLLOG-Max-SQN的性能进行评估,这些UCI数据集的详细信息如表4所示.
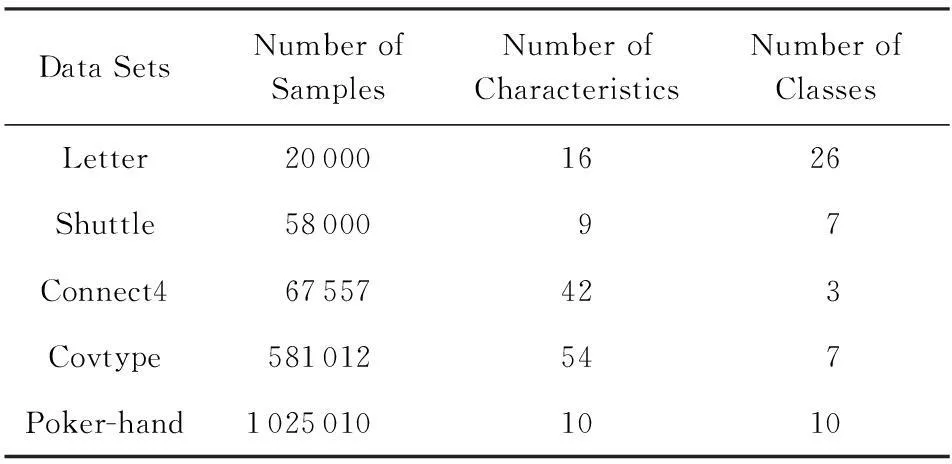
Table 4 The UCI Data Sets for Validating the Performance
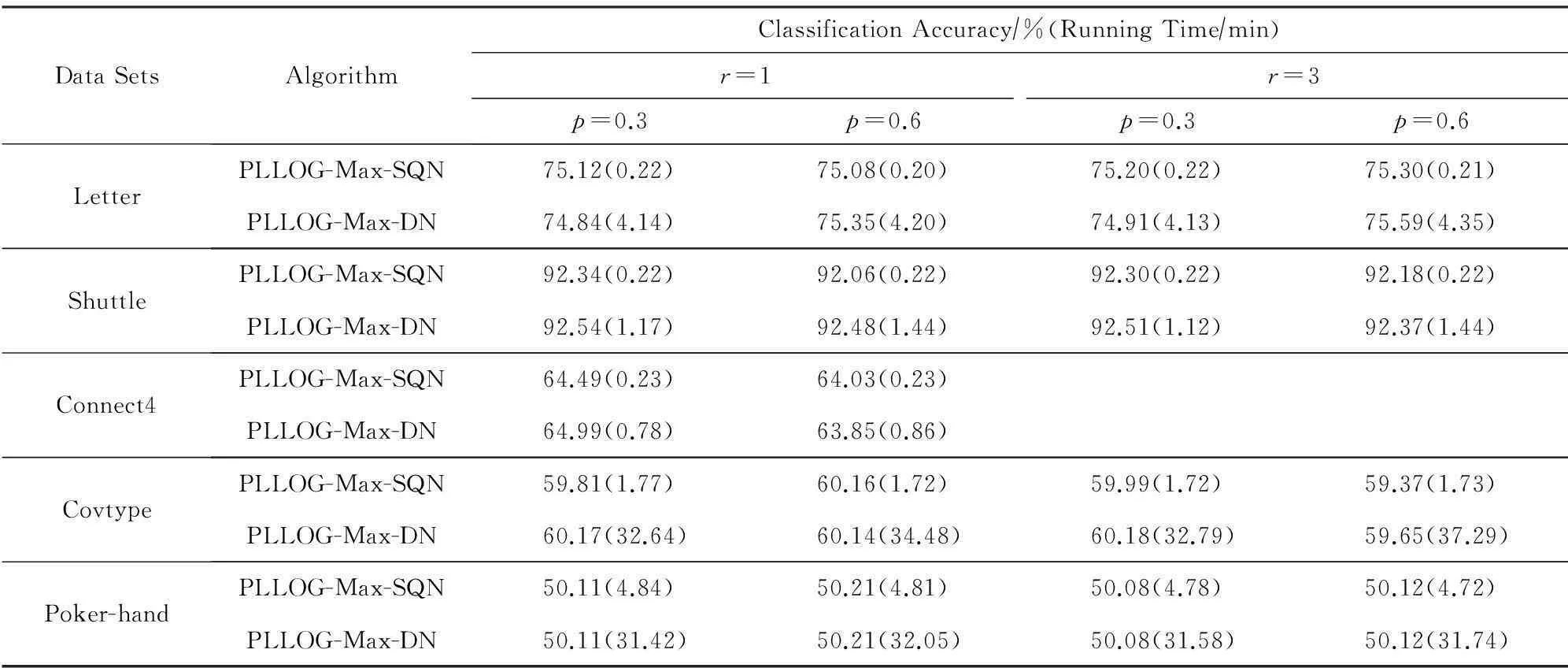
表5给出了PLLOG-Max-SQN算法按照以上的参数设定方法在各个UCI数据集上的平均预测精度和计算时间,由于目前还没有其他的快速偏标记学习算法,因此只将PLLOG-Max-SQN算法与我们建立的PLLOG-Max-DN算法进行了比较,这2个算法的结束条件是PLLOG-Max-SQN的迭代次数是2n3(n训练样本个数),PLLOG-Max-DN的迭代次数是100次,所有结果都是在CPU主频为2.5 GHz、内存为8 GB的笔记本电脑上运行得到的.
从表5可以看出,2个算法的预测精度基本都相当,但是计算时间上PLLOG-Max-SQN算法要远远快于PLLOG-Max-DN算法.为了进一步明确2个算法的预测精度之间究竟有无明显差距,我们利用5%显著性水平的t检验方法对2个算法在各个数据集上的结果进行了分析,结果表明除在2个控制数据集Shuttle(p=0.6,r=1),Connect4(p=0.6,r=1)上PLLOG-Max-DN算法比PLLOG-Max-SQN算法的精度略高以外,在其他的16个控制数据集上,这2个算法的结果在统计意义上是一样的.
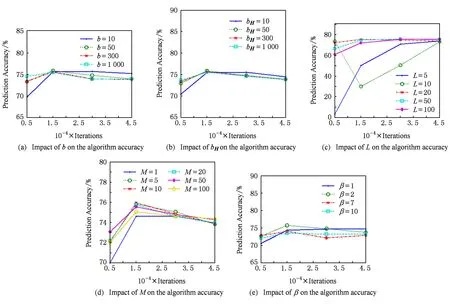
Fig. 1 The performance of PLLOG-Max-SQN algorithm on Letter data set when varying the value of each parameter.图1 每个参数取不同值时PLLOG-Max-SQN算法在Letter数据集上的性能
DataSetsAlgorithmClassificationAccuracy∕%(RunningTime∕min)r=1r=3p=0.3p=0.6p=0.3p=0.6LetterPLLOG-Max-SQN75.12(0.22)75.08(0.20)75.20(0.22)75.30(0.21)PLLOG-Max-DN74.84(4.14)75.35(4.20)74.91(4.13)75.59(4.35)ShuttlePLLOG-Max-SQN92.34(0.22)92.06(0.22)92.30(0.22)92.18(0.22)PLLOG-Max-DN92.54(1.17)92.48(1.44)92.51(1.12)92.37(1.44)Connect4PLLOG-Max-SQN64.49(0.23)64.03(0.23)PLLOG-Max-DN64.99(0.78)63.85(0.86)CovtypePLLOG-Max-SQN59.81(1.77)60.16(1.72)59.99(1.72)59.37(1.73)PLLOG-Max-DN60.17(32.64)60.14(34.48)60.18(32.79)59.65(37.29)Poker-handPLLOG-Max-SQN50.11(4.84)50.21(4.81)50.08(4.78)50.12(4.72)PLLOG-Max-DN50.11(31.42)50.21(32.05)50.08(31.58)50.12(31.74)
4结束语
损失函数的设计体现了算法关于学习框架本质的刻画,是影响算法泛化性能的关键因素之一.最大值损失函数可以较均值损失函数更好地描述偏标记学习框架下的样本与标记之间的关系,但是由于最大值损失函数是一个非光滑函数,导致建立模型的目标函数通常也是一个难于求解的非光滑函数,针对这个问题,本文通过引入凝聚函数,将基于最大值损失函数的偏标记学习模型的目标函数转换成了一种易于求解的光滑凹函数.此外,针对已有算法不能处理大数据的问题,本文通过引入随机拟牛顿法对模型进行求解,建立一种快速偏标记学习算法,可以有效处理大数据.考虑到本文建立的算法是一种线性算法,有时不能很好地处理非线性问题,下一步我们将尝试以支持向量机或者高斯过程模型为建模工具,建立一种基于核方法的快速偏标记学习算法.
参考文献
[1]Zhang Minling. Research on partial label learning[J]. Journal of Data Acquisition & Processing, 2015, 30(1): 77-87 (in Chinese)(张敏灵. 偏标记学习研究综述[J]. 数据采集与处理, 2015, 30(1): 77-87)
[2]Cour T, Sapp B, Taskar B. Learning from partial labels[J]. Journal of Machine Learning Research, 2011, 12: 1501-1536
[3]Zhang Minling. Disambiguation-free partial label learning[C]Proc of the 14th SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2014: 37-45
[4]Luo J, Orabona F. Learning from candidate labeling sets[C]Advances in Neural Information Processing Systems. Montreal: Neural Information Processing System Foundation, 2010: 1504-1512
[5]Hüllermeier E, Beringer J. Learning from ambiguously labeled examples[J]. Intelligent Data Analysis, 2006, 10(5): 419-439
[6]Liu L, Dietterich T. A conditional multinomial mixture model for superset label learning[C]Advances in Neural Information Processing Systems. Montreal: Neural Information Processing System Foundation, 2012: 557-565
[7]Zeng Z, Xiao S, Jia K, et al. Learning by associating ambiguously labeled images[C]Proc of the 26th IEEE Int Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2013: 708-715
[8]Grandvalet Y, Bengio Y. Learning from partial labels with minimum entropy, 2004s-28[R]. Montreal: Center for Interuniversity Research and Analysis of Organizations, 2004
[9]Fung G, Dundar M, Krishnapuram B, et al. Multiple instance learning for computer aided diagnosis[C]Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2007: 425-432
[10]Grandvalet Y. Logistic regression for partial labels[C]Proc of the 9th Int Conf on Information Processing and Management of Uncertainty in Knowledge-Based Systems. Annecy, Haute-Savoie: Institute for the Physics and Mathematics of the Universe (IPMU), 2002: 1935-1941
[11]Jin R, Ghahramani Z. Learning with multiple labels[C]Advances in Neural Information Processing Systems. Montreal: Neural Information Processing System Foundation, 2002: 897-904
[13]Nguyen N, Caruana R. Classification with partial labels[C]Proc of the 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2008: 381-389
[14]Li C, Zhang J, Chen Z. Structured output learning with candidate labels for local parts[C]Proc of the European Conf on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECMLPKDD 2013). Berlin: Springer, 2013
[15]Li X. An aggregate function method for nonlinear programming[J]. Science in China Series A-Mathematics, 1991, 34(12): 1467-1473
[16]Horn R, Johnson C. Topics in Matrix Analysis[M]. Cambridge, UK: Cambridge University Press, 1991: 239-297
[17]Byrd R, Hansen S, Nocedal J, et al. A stochastic quasi-Newton method for large-scale optimization[OL]. [2015-02-18]. http:arxiv.orgpdf1401.7020v2.pdf
[18]Nocedal J, Wright S. Numerical Optimization[M]. 2nd ed. Berlin: Springer, 1999: 195-204
[19]Yuille A, Rangarajan A. The concave-convex procedure[J]. Neural Computation, 2003, 15(4): 915- 936
[20]Bache K, Lichman M. UCI machine learning repository[OL]. 2013 [2015-03-10]. http:archive.ics.uci.eduml

Zhou Yu, born in 1982. PhD candidate. Her research interests include machine learning and data mining.

He Jianjun, born in 1983. PhD and lecturer. His research interests include machine learning and pattern recognition.

Gu Hong, born in 1961. Professor and PhD supervisor. His research interests include machine learning, big data and bioinformatics.

Zhang Junxing, born in 1969. PhD and professor. His research interests include data mining and speech signal processing.
A Fast Partial Label Learning Algorithm Based on Max-loss Function
Zhou Yu1, He Jianjun1,2, Gu Hong1, and Zhang Junxing2
1(FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024)2(CollegeofInformationandCommunicationEngineering,DalianNationalitiesUniversity,Dalian,Liaoning116600)
AbstractIn the age of big data, learning with weak supervision has become one of the hot research topics in machine learning field. Partial label learning, which deals with the problem where each training example is associated with a set of candidate labels among which only one label corresponds to the ground-truth, is an important weakly-supervised machine learning frameworks proposed recently and can be widely used in many real world tasks. The max-loss function may be used to accurately capture the relationship between the partial labeled sample and its labels. However, since the max-loss function usually brings us a nondifferentiable objective function difficult to be solved, it is rarely adopted in the existing algorithms. Moreover, the existing partial label learning algorithms can only deal with the problem with small-scale data, and rarely can be used to deal with big data. To cure above two problems, this paper presents a fast partial label learning algorithm with the max-loss function. The basic idea is to transform the nondifferentiable objective to a differentiable concave function by introducing the aggregate function to approximate the max(·) function involved in the max-lass function, and then to solve the obtained concave objective function by using a stochastic quasi-Newton method. The experimental results show that the proposed algorithm can not only achieve higher accuracy but also use shorter computing time than the state-of-the-art algorithms with average-loss functions. Moreover, the proposed algorithm can deal with the problems with millions samples within several minutes.
Key wordspartial label learning; max-loss function; aggregate function; weakly-supervised learning; classification accuracy
收稿日期:2015-03-26;修回日期:2015-07-13
基金项目:国家自然科学基金项目(61503058,61374170,61502074,U1560102);高等学校博士学科点专项科研基金项目(20120041110008);中央高校基本科研业务费专项资金项目(DC201501055,DC201501060201)
通信作者:顾宏(guhong@dlut.edu.cn)
中图法分类号TP391
This work was supported by the National Natural Science Foundation of China (61503058,61374170,61502074,U1560102), the Research Fund for the Doctoral Program of Higher Education of China (20120041110008), and the Fundamental Research Funds for the Central Universities (DC201501055,DC201501060201).

