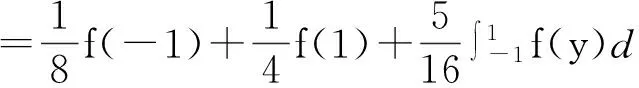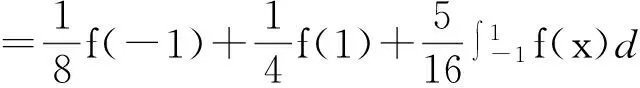混合型随机变量数字特征的计算

胡晓山，　刘继成

(华中科技大学数学与统计学院， 武汉430074)



混合型随机变量数字特征的计算

胡晓山，刘继成

(华中科技大学数学与统计学院， 武汉430074)

[摘要]利用分布函数的广义反函数，将随机变量表示为均匀分布随机变量的函数，然后用随机变量函数的数学期望公式可计算原随机变量的数字特征，该方法适用于所有类型的随机变量. 最后，利用四种不同方法计算了一个混合型随机变量的数字特征, 说明了这些方法的异同.

[关键词]混合型随机变量； 数字特征； 广义反函数

1问题的提出

对于一般随机变量期望的定义，要么通过概率空间上的积分给出，要么通过分布函数的Lebesgue-Stieltjes 积分给出.具体地，设随机变量X定义在概率空间(Ω,F,P)上，X的数学期望定义为

EX=∫ΩX(ω)dP(ω)，

其中要求积分存在. 该积分是定义在概率空间(Ω,F,P)上的，这需要测度论的知识.若X的分布函数为F(x)，则

(1)

其中等式右边的积分应理解为Lebesgue-Stieltjes 积分, 这需要实变函数的知识. 用测度论中的知识可以证明：(1)中的两个积分有一个存在，另一个就存在，且二者相等.

基于此，目前多数工科概率论与数理统计教材中，只给出了离散型随机变量和连续型随机变量数学期望的定义及相关计算. 若X为离散型随机变量，pk=P(X=xk)，k≥1为其分布列，则X的数学期望定义为

(2)

其中要求级数绝对收敛. 此时，X的分布函数F(x)是一个跳跃函数，它在每个xk处的跳跃度为pk.对跳跃函数F(x)，(1)式右边等于(2)式的右边. 若X为连续型随机变量，p(x)为其密度函数，则X的数学期望定义为

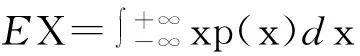
(3)

其中要求积分绝对收敛. 此时，dF(x)=p(x)dx，(1)式右边与上式右边的积分相等.

但是在应用中，经常会遇到既非离散型，也非连续型的随机变量，统称为混合型随机变量 (见例1). 通常的教材中并没有介绍如何求混合型随机变量的数学期望. 为了克服上面Lebesgue-Stieltjes 积分的困难，文献[2]本质上用分部积分公式将Lebesgue-Stieltjes 积分化为Lebesgue积分(通常情形与Riemann积分相等)来计算混合型随机变量的期望和方差. 文献[2]定理4的结果是：对正整数k，

(4)

注意到，在工科概率论与数理统计教材中，都会不加证明地叙述如下求随机变量函数数学期望的公式——“佚名统计学家公式”(参见[3] P198). 亦即，若X为连续型随机变量，p(x)为其密度函数，则Y=g(X)的数学期望为

(5)

其中要求积分绝对收敛.

本文的思路是，从随机变量X的分布函数F(x)出发，将X表示为[0,1]区间上均匀分布的随机变量Y的函数，然后应用公式(5)来求X的数字特征.

2主要结论

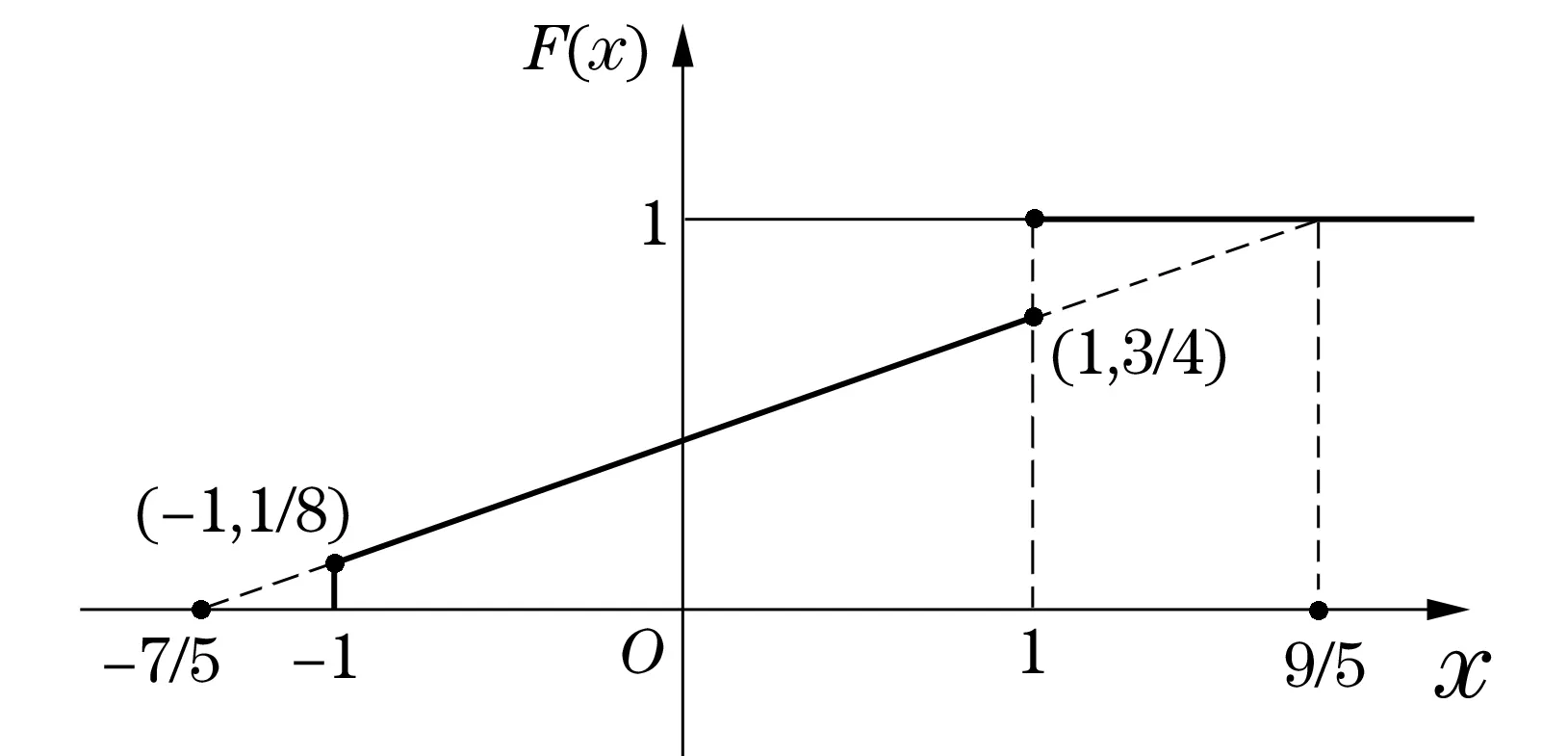
设随机变量X的分布函数为F(x), 对0

图1

F-1(x)称为F(x)的广义反函数 (图1，参见[1]P26).显然，若F(x)严格单调增，F-1(x)即为F(x)的反函数.

广义反函数具有下面的性质：

(i) 由于F(+∞)=1，所以{y∶F(y)≥x}≠∅，因此F-1(x)的定义是合理的；

(ii) 当x1

(iv) 对每个0

{y∶F-1(y)≤x}={y∶y≤F(x)}.

(6)

事实上，由F-1(y)的定义，它是满足y≤F(x)的最小的x，因此(6)式右边包含于左边；又因为F(x)是单调不降函数和性质(iii)，因此(6)式左边包含于右边.

设Y～U[0,1], 由(5)式有

P(F-1(Y)≤x)=P(Y≤F(x))=F(x)，

即X与F-1(Y)同分布. 因此，由佚名统计学家公式有

(7)

特别地，对正整数k

由此可以计算X的期望和方差.

注公式(4)与(7)相比，(7)能够计算除了原点矩外的其他数字特征.

3应用举例与方法比较

本节将用上面提到的4种方法计算下面的例子，从中可以看出这些方法有何异同.

例1设随机变量X的分布函数F(x)为

求EX和DX.

图2

方法1设随机变量Y的分布函数

FY(x)与F(x)的关系如图2所示: 即

则X与min{max{Y,-1},1}同分布. 对任意Borel可测函数f，由佚名统计学家公式得

Ef(X)=Ef(min{max{Y,-1},1})

因此

和

方法2X的分布函数F(x)可以分解为

其中

方法3由公式(4), 有

和

图3

方法4F(x)的广义反函数如图3所示，表达式为

因此，由公式(7), 有

特别地

方法比较方法1具有特殊性，比如当分布函数有多个跳跃点时随机变量Y的构造是困难的；方法3只能计算原点矩，对其他数字特征无效；方法2和方法4都有普遍的适用性，本质上方法2是Lebesgue-Stieltjes，但理解该积分需要更深的数学知识，方法4把问题归结为较初等的范畴. 综上，方法4适用范围广，且能够为本科学生接受.

[参考文献]

[1]刘次华. 概率论与数理统计[M].2版. 武汉：华中科技大学出版社，2012.

[2]宁荣健，余丙森. 基于分布函数的混合型随机变量数学期望和方差的计算[J].大学数学，2015，31(2)：48-52.

[3]李贤平，概率论基础[M].3版. 北京：高等教育出版社，2010.

[4]李贤平，陈子毅. 概率论基础学习指导书[M]. 北京：高等教育出版社， 2011.

The Computing Method to Numerical Characteristics of Mixed Type Random Variables Based on Generalized Inverse Functions

HUXiao-shan，LIUJi-cheng

(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:By using the generalized inverse function of distribution function，a random variable can be expressed as the function of an uniformly distributed random variable, then the numerical characters of original random variables can be calculated by a mathematical expectation formula for functions of random variable, this method may be applied to all of random variables. Finally, numerical characteristics of a mixed-type random variable are calculated using four different methods, which show the differences between these methods.

Key words:mixed type random variables; numerical characteristics; generalized inverse function

[收稿日期]2015-06-22；[修改日期] 2016-01-14

[基金项目]华中科技大学自主创新研究基金(2014TS066)；华中科技大学教学研究项目(2015067)

[作者简介]胡晓山(1966-),男，博士，副教授，从事概率统计研究.Email: hxs@hust.edu.cn[通讯作者]刘继成(1976-)，男，博士，副教授，从事概率统计研究.Email： jcliu@hust.edu.cn

[中图分类号]O211.3

[文献标识码]C

[文章编号]1672-1454(2016)02-0086-05