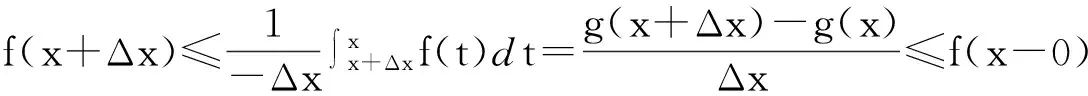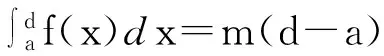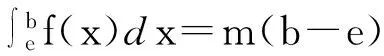关于积分中值定理的逆问题

王良成，　杨明硕，　袁南桥

(重庆师范大学涉外商贸学院，重庆401520)



关于积分中值定理的逆问题

王良成，杨明硕，袁南桥

(重庆师范大学涉外商贸学院，重庆401520)

[摘要]当函数严格单调时，本文证明了积分中值定理中值点的唯一性. 且较完整地解决了该定理的逆问题，其证明也相当简洁.

[关键词]积分中值定理； 严格单调函数； 逆问题； 唯一性

1引言

在数学分析(如文[1])中，有如下众所周知的积分中值定理.

定理A设f(t)在[a,b]上连续.则存在c∈(a,b)使得

(1.1)

上述定理中的c不唯一.文[2]给出了上述定理的逆不一定成立的例子，并改变条件给出了上述定理的如下逆定理.

定理B设f(t)是[a,b]上严格单调函数，则存在点x0∈(a,b)，满足

(i)当ξ∈(a,x0)时，存在唯一点d∈(a,b)，使

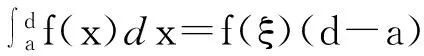
(1.2)

(ii)当ξ∈(x0,b)时，存在唯一点e∈(a,b)，使

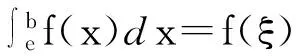
(1.3)

上述d与e的范围太宽，定理B中的结果不完整，证明也较繁琐；该文[2]在其注2中还表述：“在定理B的条件下，若f(t)在[a,b]上还是连续的，则定理B的x0就是定理A中的c”，事实上这种表述对x0与c的关系未彻底弄清楚.本文在定理B的条件下给出比 (1.1)至(1.3)三式更弱的表达式，获得了比定理B更完整的结论，彻底解决了上述x0与c的关系，其证明也相当简洁.

2两个引理

为证明本文定理，还须如下引理.

(i) g(x)是[a,b]上的连续严格凸(凹)函数；

(ii) ∀x∈(a,b)，则g′-(x)=f(x-0)，g′+(x)=f(x+0).

证不妨设f(t)在[a,b]上是严格单调递增的.

(i) 对∀x,y∈[a,b]，x

λg(x)+(1-λ)g(y)-g(λx+(1-λ)y)

(2.1)

即g(x)是[a,b]上的严格凸函数.由文[1]中的定理7.4知g(x)在[a,b]上是连续的.

(ii) 对∀x∈(a,b)，Δx<0，∀t∈[x+Δx,x]⊂[a,b]，则有

f(x+Δx)≤f(t)≤f(x-0).

(2.2)

上式对t在[x+Δx,x]上积分，并除以-Δx，则有

(2.3)

对上式让Δx→0-0，则有g′-(x)=f(x-0). 同理可证g′+(x)=f(x+0).

当f(t)在[a,b]上是严格单调递减的，则(2.1)，(2.2)与(2.3)三式不等号反向成立.(2.1) 式不等号反向意味着g(x)是[a,b]上的严格凹函数；(2.2)与(2.3)不等号反向亦可得(2)的结果.

引理2[3]设g(t)是[a,b]上的连续严格凸函数, 则有如下三个结果.

(i) 存在唯一的c∈(a,b)使得

g′-(c)(b-a)≤g(b)-g(a)≤g′+(c)(b-a);

(2.4)

(ii) 对∀ξ∈(a,c)及g′-(ξ)≤m≤g′+(ξ)，则存在唯一的d∈(ξ,b)使得

g(d)-g(a)=m(d-a),

(2.5)

反之对上述的d，只有a才能使上式成立.且对∀r∈(a,ξ)，则存在唯一的s∈(ξ,d)，使得

g(s)-g(r)=m(s-r)，

(2.6)

反之对∀s∈(ξ,d)，则存在唯一的r∈(a,ξ)才能使上式成立.

(iii) 对∀ξ∈(c,b)及g′-(ξ)≤m≤g′+(ξ), 则存在唯一的e∈(a,ξ)使得

g(b)-g(e)=m(b-e),

(2.7)

反之对上述的e,只有b才能使上式成立.且对∀u∈(ξ,b), 则存在唯一的v∈(e,ξ)使得

g(u)-g(v)=m(u-v)，

(2.8)

反之对∀v∈(e,ξ)，则存在唯一的u∈(ξ,b)才能使上式成立.

当g(t)是[a,b]上的连续严格凹函数时，则(i)-(iii)中的不等式均反向.

3主要结果

定理设f(t)是[a,b]上严格单调递增函数, 则有如下三个结果.

(i) 存在唯一的c∈(a,b)使得

(3.1)

又若f(t)在c处连续，则上式变为

(3.2)

(ii) 对∀ξ∈(a,c)及f(ξ-0)≤m≤f(ξ+0)，则存在唯一的d∈(ξ,b)使得

(3.3)

又若f(t)在ξ处连续，则上式变为

(3.4)

反之对上述的d，只有a才能使上两式成立.且对∀r∈(a,ξ)，则存在唯一的s∈(ξ,d)，使得

(3.5)

又若f(t)在ξ处连续，则上式变为

(3.6)

反之对∀s∈(ξ,d)，则存在唯一的r∈(a,ξ)才能使上两式成立.

(iii) 对∀ξ∈(c,b)及f(ξ-0)≤m≤f(ξ+0), 则存在唯一的e∈(a,ξ)使得

(3.7)

又若f(t)在ξ处连续，则上式变为

(3.8)

反之对上述的e,只有b才能使上两式成立.且对∀u∈(ξ,b), 则存在唯一的v∈(e,ξ)使得

(3.9)

又若f(t)在ξ处连续，则上式变为

(3.10)

反之对∀v∈(e,ξ)，则存在唯一的u∈(ξ,b)才能使上两式成立.

当f(t)是[a,b]上的严格单调递减函数时，则(i)-(iii)中的不等式均反向.

注1(3.1)式中的c即为定理B中x0，(3.2)式中的c即为定理A中c，当f(t)在[a,b]上是严格单调函数时(不论连续与否)，定理B中x0与c是相同的且唯一. (1.2)与(1.3)两式分别是(3.3)与(3.7)两式的特殊情况，(1.2)与(3.3)式中的d相同，(1.3)与(3.7)式中的e相同，d与e的范围后者较前者好.

注2本文的主要定理的证明还可仿照引理2的证法去证明.

[参考文献]

[1]华东师范大学数学系.数学分析(上)[M].3版.北京:高等教育出版社,2001.

[2]郭辉,等. 积分中值定理逆问题及其渐近性[J]. 数学的实践与认识, 2002,32(6)：1031-1036.

[3]王良成，等. 关于Lagrange微分中值定理的逆问题[J]. 大学数学, 2012,28(5)：140-143.

On Inverse Problem of Integral Mid-VaIue Theorem

WANGLiang-cheng，YANGMing-shuo，YUANNan-qiao

(Chongqing Normal University, Foreign Trade And Business College, Chongqing 401520, China)

Abstract:When the function is strictly monotone, we prove the uniqueness of mid-value point for integral mid-vaIue theorem. And we obtain a complete solution for the inverse problem of this theorem. And this proof is quite simple also.

Key words:integral mid-value theorem; strictly monotone function; inverse problem; uniqueness

[收稿日期]2015-12-01

[基金项目]重庆师范大学涉外商贸学院重点科研项目(KY2015001)

[作者简介]王良成(1949—)，男，学士，教授，从事凸分析研究.Email：wlc@cqut.edu.cn

[中图分类号]O178

[文献标识码]C

[文章编号]1672-1454(2016)02-0078-03