基于分形市场假说的金融时间序列的分形特征的解析

马芙玲

(中山火炬职业技术学院公共课部，广东中山528436)



基于分形市场假说的金融时间序列的分形特征的解析

马芙玲

(中山火炬职业技术学院公共课部，广东中山528436)

[摘要]证券收益率序列中普遍存在分形特征,但其形成原因却鲜为人知.本文根据分形市场假说构建了博弈模型，对证券收益率序列中分形特征的形成原因进行了解.结果表明,分形市场假说是证券收益率序列具有分形特征的充分条件.

[关键词]分形时间序列； 分形市场假说； 成因解析

1引言

随着分形统计分析的发展，证券收益率序列普遍存在分形特征已日益被施锡铨和艾克凤(2004)[1]、Shi等(2014)[2]等国内外众多学者所证实.然而，时至今日，仍很少有学者对证券收益率序列中为何存在分形特征进行研究.学者们对证券收益率序列中存在分形特征的密切关注源自Peters (1994)[3]的分形市场假说(Fractal Market Hypothesis, FMH).虽然FMH指出了证券收益率序列会存在分形特征，但并没有给出存在分形特征的数学证明.那么，能否从FMH推出证券收益率序列存在分形特征，对普遍存在的分形特征的原因给予解释呢？本文以FMH为基础，创新性的构建了博弈过程,并通过对博弈模型展开分析，对该问题给予了肯定的回答，从而为FMH提供了坚实的数学基础，同时，本文提出的博弈模型也有益于丰富和发展金融博弈模型.

2理论与仿真

FMH被Peters(1994)[3]公之于世，现已被Zunino等(2008)[4]、王鹏等(2009)[5]、宋光辉等(2013)[6]等大量学者接受.FMH对投资者的行为选择具有如下假设：

2.1理论模型

和

并将si,m(t)对应的行动记为Ai,m(t)∈A.

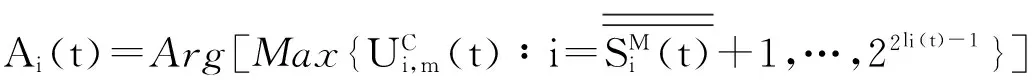
(1)

(2)

A(t)=A1(t)×V1(t)+…+AN(t)×VN(t).

(3)

(4)

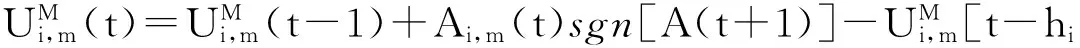
(5)

投资者的通过上述博弈过程所做出的行动决策通过体现在Ai(t)上，市场中所有投资者的决策结果汇总即为A(t)，A(t)代表着该时刻的证券过度需求.刘兴华和杨建梅(2007)[9]指出，证券t在时刻的收益率Rt=Nt-1×A(t). 因此，A(t)的波动引致证券的收益率发生波动.综上可见，从FMH中对投资者行为假设出发，可以得出证券收益率Rt. 如果投资者按照FMH进行投资操作之后，证券的收益率序列一定会表现出分形特征，即FMH是证券收益率序列呈现分形特征的原因；那么，按照上述博弈过程所得到的收益率Rt的序列将出现分形特征.由于直接求解出上述博弈过程所得到的收益率非常困难，下文通过仿真分析判别收益率序列是否存在分形特征，进而回答利用FMH能否对证券收益率序列中的分形特征给予解释.

2.2仿真分析

本文的原始序列为2004年1月2日至2014年1月30日间上海证券交易所发布的所有行业指数的日收盘价，数据来源于聚源数据库.仿真时，取Nt=1001, hi(t)=3, mi(t)≤3, ci(t)=0.005; 且当出现策略成功率相同的情形时，假设投资者随机选择策略.为了防止此处随机选择策略可能会对比较分析仿真和真实对数收益率序列产生影响，本文对所有行业指数的仿真和真实值先求均值再进行比较.利用Matlab7.0可求出仿真收益率序列，为了形象，如下图1同时将真实与仿真收益率序列的波动趋势进行了罗列：

为了证明利用FMH可以对证券收益率序列中的分形特征给予解释，下文对真实和仿真收益率序列的分形特征进行分析.判别时间序列分形特征的常用方法之一是Kantelhardt等(2002)[10]提出的多重分形去趋势波动分析法(Multifractal Detrended Fluctuation Analysis, MF-DFA).其主要的步骤如下：

图1　真实与仿真收益率序列

第四步： 计算第m个子序列消除局部趋势后剩余序列的方差，得到如下(6)式所示的去趋势波动方程.为了防止如下(6)式为0，常常要求s≥l+2

(6)

第五步： 按如下(7)式计算q阶结构化分割函数Fq(s).q的变动有利于辨别序列中不同程度的波动，当q取较大的正值或较小的负值时，较大或小的Fm(s)受到Fq(s)的重视.

(7)

MF-DFA不仅能判断时间序列中是否有分形特征，还能对单分形和多重分形特征做出区别，且具有简单易行和对时间序列的平稳性没有要求等众多优点，因而被Zunino等(2008)[4]和王鹏等(2009)[5]等国内外学者广泛应用.利用MF-DFA对仿真与真实收益率序列的分析结果如图2.

图2　真实与仿真收益率序列的多重分形分析

由图2可知，仿真收益率序列如同真实的收益率序列，具有出分形特征，且是多重分形.可见，投资者按照FMH进行投资操作之后，证券的收益率序列一定会表现出分形特征.因此，利用FMH可以对证券收益率序列的分形特征做出解释，FMH是证券收益率序列具有分形特征的充分条件.需要说明的是，图2中仿真收益率序列h(q)总是偏高，其原因在于本文基于仿真的便利，在参数设置时，对市场参与者人数Nt设置远小于实际市场的参与者，同时对投资者i在时刻t对价格序列的关注长度mi(t)，以及投资者i在时刻t对私人信息的记录长度hi(t)也设定的比实际的情况要小，这样会导致仿真收益率相比实际收益率序列有更大的波动(见前文图1)，从而由前文(7)式可知会导致Fq(s)偏高，最终导致h(q)偏高.

3小结

本文针对证券收益率序列存在分形特征但其原因鲜为人知的现实背景，通过构建博弈模型和仿真分析表明，投资者根据FMH对证券进行投资交易，证券收益率序列必然会表现出分形特征.因而，可以利用FMH对证券收益率序列的分形特征做出解释.本文的结果深化了对分形时间序列的相关研究，为FMH提供了数理基础，为FMH和分形时间序列之间的关系提供了数理基础.本文仍存在一些不足.一是本文的模型无法直接计算出收益率的波动趋势.二是本文定量分析仍显欠缺.对这些缺陷进行弥补是未来重点研究内容之一.

[参考文献]

[1]施锡铨,艾克凤. 股票市场风险的多重分形分析[J]. 统计研究, 2004, 21(9): 33-36.

[2]Shi W B, et al. Multiscale Multifractal Detrended Cross-correlation Analysis of Financial Time Series[J]. Physica A, 2014, 403(6): 35-44.

[3]Peters E E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics[M]. New York: John Wiley & Sons Inc., 1994.

[4]Zunino L, et al. A Multifractal Approach for Stock Marke Inefficiency[J]. Physica A, 2008, 387(26): 6558-6566.

[5]王鹏, 魏宇, 张蕾. 中国交易所债券市场分形特征的实证研究[J]. 数理统计与管理, 2009, 28(2): 324-330.

[6]宋光辉, 吴栩, 詹素卿，等. 行业指数相关关系的多重分形时变性及实证分析[J]. 统计与信息论坛, 2013, 28(7): 32-36.

[7]Challet D, et al. Modeling Market Mechanism with Minority Game[J]. Physca A: Statistical Mechanics and its Applications, 2000, 276(2): 284-315.

[8]Andersen J V, Didier S. The $-game[J]. The European Physical Journal B, 2003, 31(1): 141-145.

[9]刘兴华, 杨建梅. 多样性和归纳推理与证券市场动力机制[J]. 系统工程理论与实践, 2007, 27(5): 35-41.

[10]Kantelhardt J W, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A, 2002, 316(1):87-114.

Analysis of Fractal Features of Financial Time Series Based on Fractal Market Hypothesis

MAFu-ling

(Department of Public Courses, Zhongshan Torch Polytechnic, Zhongshan Guangdong 528436, China)

Abstract:Fractal characteristics exist in the sequence of securities’ yields, but people rarely know the reasons for the formation. This paper constructs the game model based on the fractal market hypothesis, and use it explains the cause of formation of fractal features. The results show that the fractal market hypothesis can explain the reasons of the fractal characteristics in the sequence of securities’ yields.

Key words:fractal time series; fractal market hypothesis; cause analysis

[收稿日期]2015-09-14；[修改日期] 2016-03-25

[作者简介]马芙玲(1963-)，女，副教授，从事数理金融研究. Email: flima@sina.com

[中图分类号]F830.91

[文献标识码]B

[文章编号]1672-1454(2016)02-0026-04