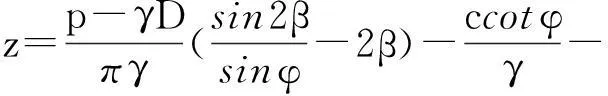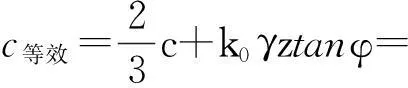考虑土体自重应力场的拱效计算方法

杨雪强, 刘勇健, 吉小明

(广东工业大学 土木与交通工程学院，广东 广州 510006)



考虑土体自重应力场的拱效计算方法

杨雪强, 刘勇健, 吉小明

(广东工业大学 土木与交通工程学院，广东 广州 510006)

摘要:抗滑桩是用于加固边坡，防止边坡滑移失稳的主要措施，土拱体易在桩间形成.本文将桩间土拱简化为水平拱，并假定处于平面应变状态，在考虑土体自重应力场前提下，对桩侧摩阻力为拱座的拱体计算方法进行了研究，揭示了土体的自重应力场对桩土拱体的量化影响.研究结果表明：自重应力场的存在对桩间土拱效应起着明显的加强作用，不考虑土体的自重应力场，也就是把土体看成是无重介质，进行桩土拱体模式的设计过于安全.

关键词:抗滑桩； 成拱效应； 等效内聚力； 自重应力； 桩间距

抗滑桩是目前加固边坡防止边坡滑移失稳的主要措施.抗滑桩的设计理念是采用非连续桩体结构，利用土体自身强度与差异变形形成的土拱[1-6]将边坡的水平滑坡推力传递到桩身，然后再通过桩身把该水平滑坡推力传递至深部稳定土层中，这样来达到安全设计的目的.

对边坡工程，通常按照不平衡荷载传递系数法计算出水平滑坡推力，设计时考虑桩结构的抗滑力与边坡的水平滑坡推力相平衡，在此基础上利用土拱效应对桩截面尺寸及桩间距进行合理设计.在此设计过程中，由于问题的复杂性，往往忽略了已客观存在的重力场对桩间土拱效应的影响，现有的文献也较少对这一问题进行研究.

本文将桩间土拱简化为水平拱，并假定处于平面应变状态，在考虑土体自重应力场的前提下，重点对桩侧摩阻力为拱座的拱体计算方法[7-9]进行了研究，揭示了土体的自重应力场对桩土拱体的量化影响.

1合理拱轴线的确定

文献[2]认为土拱效应主要是利用岩土体抗压性能好、抗拉能力差的特点，是岩土体不均匀变形后受力的自我优化调整的结果.文献[3]认为土拱由土体不均匀变形的应力传递和调整而自发形成，是调整自身抗剪强度以抵抗外力的结果，所产生的拱形必然使土体介质能最大限度地发挥其强度作用，土体中沿最大主应力方向的迹线就是“合理拱轴线”.因此，在滑坡推力均匀作用下，合理的拱轴线应为二次抛物线，如图1所示.

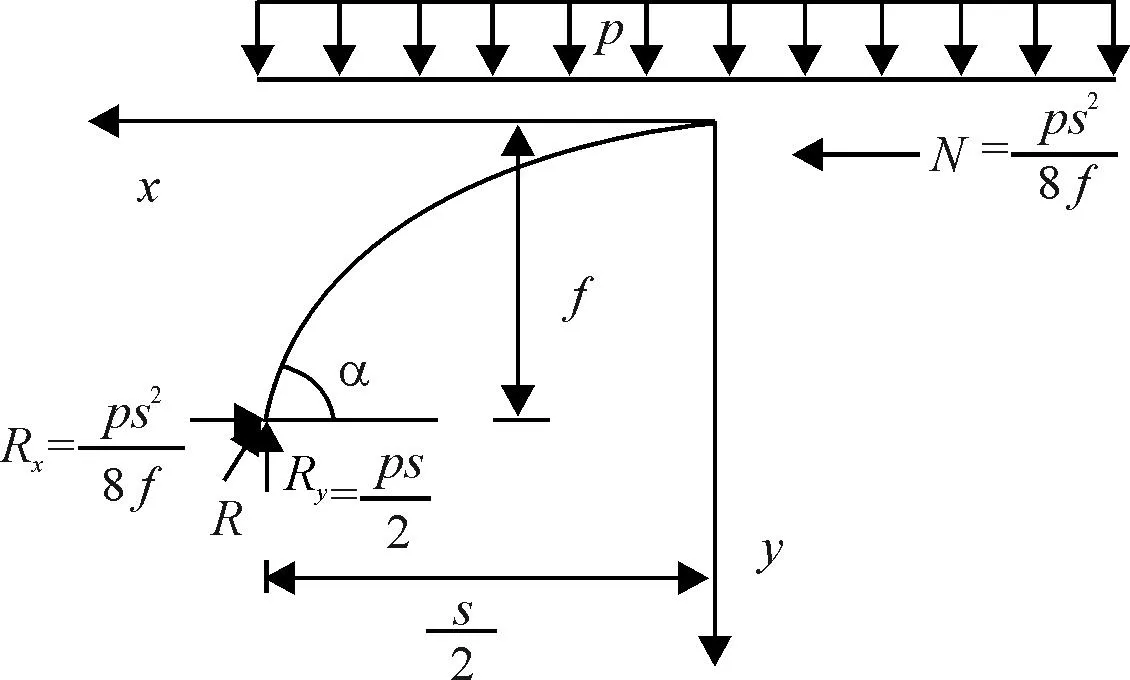
图1　合理的拱轴线

在均布荷载下，图1所示的抛物线拱的力学特点是拱轴线上处处横截面均无弯矩和剪力，沿拱轴线的切线方向仅受均匀的轴向压力，满足文献[2-3]的要求，抛物线方程式表达为

y=4fx2/s2，

(1)

式中f、s分别为土拱矢高和跨度.

据图1的静力平衡方程可知，拱轴上任一点x处的水平推力为ps2/(8f)、垂直支撑力为px，合力

N及其斜率分别表达为

(2)

tanα=dy/dx=8fx/s2.

(3)

很显然，拱脚横截面上的正应力达到最大值，为最不利的受压截面.所以，拱体的破坏最先从拱脚开始，然后逐步向拱顶处转移扩展.

文献[10]研究指出，在边坡中设置的抗滑桩，依赖桩侧摩阻力为拱座形成的土拱是土坡抗滑桩承担滑坡推力的主要承载土拱体.因此本文侧重于桩侧摩阻力为拱座形成的土拱，来研究土体自重应力场对其影响.

2不考虑土体自重应力场的拱效计算

设迎荷面矩形桩的尺寸为d,桩身侧面的尺寸为b，桩间净距为s.如桩身侧面的摩阻力起着拱座的作用，桩间土体的成拱效应如图2所示，则拱轴线的方程式与式(1)相同，拱脚处的Rx、Ry和合力R分别表达为

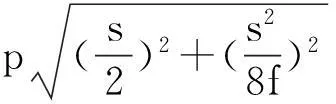
(4)

图2　桩身侧面起着拱座的拱体

2.1桩侧界面的力学参数为c、φ

如图2(b)所示，桩土界面即为破裂面，据极限平衡理论，桩土界面与最大主应力作用面的夹角为(45°+φ/2)，则可推知拱体厚度t的表达式为

t=b·cos(45°+φ/2).

(5)

如图2(b)所示，基于拱轴线方程式(1)，建立拱脚处的斜率表达式为

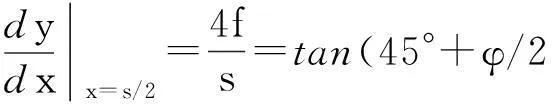
(6)

如图2(a)所示，在桩土界面，依据Mohr-Coulomb破坏准则，可建立方程式

Ry=Rxtanφ+c·b.

(7)

联立式(6)和式(7)求出两个未知量s和f，表达式为

(8)

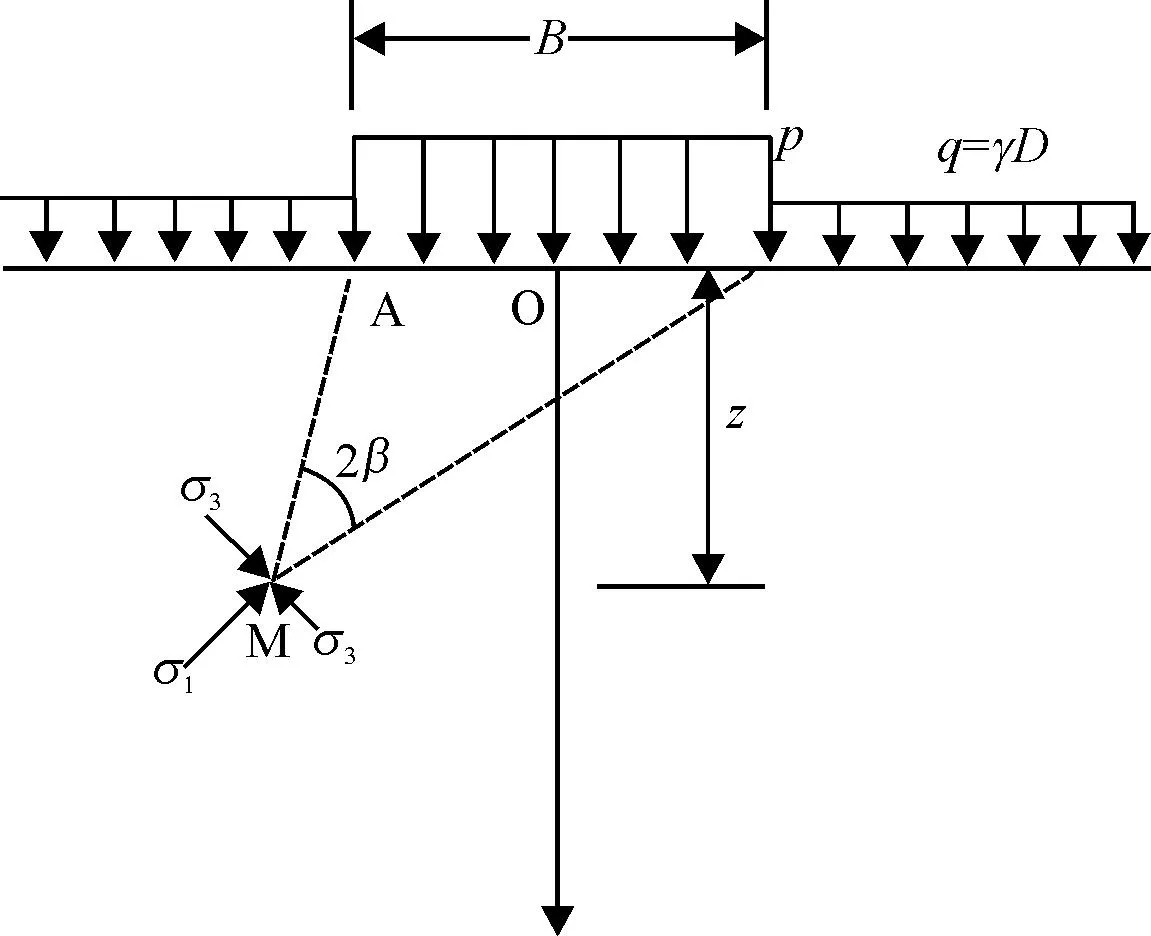
2.2桩侧界面的力学参数c1

如图2(c)所示，桩土界面为破裂面，因界面的摩擦角为φ1，该破裂面与最大主应力作用面的夹角为(45°+φ1/2)，此时拱体厚度t的表达式为

t=b·cos(45°+φ1/2)

(9)

如图2(c)所示，基于拱轴线方程式(1)，建立拱脚处的斜率表达式为

(10)

如图2(a)所示，在桩土界面，依据Mohr-Coulomb破坏准则，可建立方程

Ry=Rxtanφ1+c1·b.

(11)

所以，如已知桩土界面的c1、φ1及土体的c、φ和桩的尺寸等，联立式(10)和式(11)求出两个未知量s和f，表达为

(12)

3考虑土体自重应力场的拱效计算

这里以图3为例进行说明，正如桩的一侧有堤坝等堆载的情况，或基坑内部的工程桩受到四周坑壁的自重而对其产生的水平挤压作用.

图3　桩后推力的分布

文中第3部分是把分布推力p作为水平外力施加在桩及桩周土体上，同时不考虑土体自身自重应力场的影响，也就是把土体看成是无重介质，然后依据图2的拱体模式设计抗滑桩.

真实的应力场与上述情况是有区别的，除了不平衡分布水平推力p外，还应考虑土体重力场的影响.为简便起见，对某一深度z处，如把该处的重力场简化为球应力σp=(2k0+1)γz/3(k0为土的侧压力系数，k0=1-sinφ，γ为土体的重度)来考虑有些偏大，因土体同时存在一个由自重应力诱发的初始剪切状态，该初始剪切对土体的受力是不利的.因此考虑到自重产生的初始剪应力的不利影响，这里对球应力适当折减，取为σp=k0γz.这样作用在桩及桩周土体上的力就近似简化为水平推力p和球应力σp=k0γz两者的合成，如图3所示.

依据Mohr-Coulomb破坏准则，土体抵抗的剪应力随着球应力的增加而增加，球应力越大，则土体抵抗的剪应力就越大.若不考虑原先存在的土体重力场而仅考虑水平分布推力p的作用，这样必将低估了土体的抵抗剪应力.所以总体上讲，不考虑土体的重力场，依据图2的拱体模式设计出的抗滑桩偏于安全.

对图3而言，拱效发生在土体滑面以上的桩体之间.当滑动面较浅时，土体的自重应力较小，忽略该部分自重应力，仅依据图2的拱体模式设计出的抗滑桩相对较为合理；而当滑动面较深时，土体的自重应力较大.如仍忽略该部分自重应力，则依据图2的拱体模式设计出的抗滑桩会过于安全保守.所以，考虑土体自重应力场的拱效计算应该是拱效理论的进一步发展.

结合图3，对考虑土体自重应力场的拱效计算问题可分两步处理：第一步，依据土体的内聚力与球应力两者是可以相互转化的原理[11-13]，可把深度z处的自重平均球应力σp=k0γz转化为该处土体内聚力的增量Δc，表达为

Δc·cotφ=σp⟹Δc=k0γztanφ，

(13)

这样就把考虑自重的土体转化为新的无重介质，该新的无重介质土体对应的内摩擦角仍为φ、但其内聚力却有所增加，该增加后的内聚力c等效表达为

c等效=c+Δc=c+k0γztanφ .

(14)

第二步，把分布推力p作为水平外力施加在桩及桩周新的无重介质土体上.这样就可用第3部分的不考虑自重应力场的拱效计算方法来设计抗滑桩.

3.1土体自重平均球应力转化为土体内聚力的验证

这里以条形均布压力p下地基中塑性区界限的求解为例进行说明.如图4所示，正如文献[14]所述，点M的自重球应力近似取为γ(D+z)，则该自重球应力可转化为该处土体的内聚力增量，该处土体增加后的内聚力c等效表达为

c等效=c+γ(D+z)tanφ.

(15)

这样就把考虑自重的具有抗剪强度指标c、φ的土体转化为具有抗剪强度指标c等效、φ的无重土体.

图4　条形均布荷载下地基中应力的计算[14]

Fig.4Soil stress calculations of uniformly loaded strip foundation[14]

如图4所示，地基中任一点M由于荷载(p-γD)(D为基础的埋深)引起的附加应力为

(16)

如地基中点M处于塑性极限平衡状态，则满足关系式

(17)

将式(15)、(16)代入式(17)，整理得出地基中塑性极限平衡区界限的方程式为

(18)

式(18)与文献[14]中的公式完全一致，这说明了内聚力与土体自重球应力间相互转化的思路是正确的.

3.2考虑自重应力场的拱体矢高和跨度的计算

3.2.1桩侧界面的力学参数为c等效、φ

相类似，桩间拱体两个未知量s等效和f等效表达为

(19)

将式(14)代入式(19)得出

(20)

3.2.2桩侧界面的力学参数c1等效、φ1<φ

需说明的是，c1等效=c1+Δc=kc+Δc，k是折减系数，k<1.内聚力增量Δc是由土体自重球应力σp=k0γz转化过来的，所以不应该折减.同理，两个未知量s等效和f等效表达为

(21)

(22)

4两种方法的比较

如图3所示，初步拟定桩的矩形截面d×b=2m×3m，滑动面上桩受荷段长为10m，作用在单位厚度土层上的水平推力为100kN/m，并假定沿桩长方向的推力为矩形分布.土体的重度γ=19kN/m3，其抗剪强度指标c=60kPa、φ=24°.分别在不考虑土体自重与考虑土体自重两种情况下，对桩间拱体进行设计.

(1) 不考虑土体自重.

在不考虑土体自重情况下，当桩侧界面的力学参数为c、φ时，依据式(8)求出的s=5.06m，f=1.95m；桩土界面粗糙程度有所减弱，如取桩土界面c1=2c/3=40kPa、φ1=2φ/3=16°，依据式(12)算出的s=3.06m，f=1.02m.

(2) 考虑土体自重.

如图2所示，仅在拱脚出现塑性破坏的情况下，通过该算例可看出：(1) 桩侧桩土界面粗糙程度对拱体跨度s与矢高f的计算结果影响较大，桩侧界面粗糙程度的降低将导致桩间净距和矢高的明显降低.(2) 在不考虑土体自重情况下，在沿深度均布推力作用下，拱体跨度s与矢高f均为常数，它们不随土体深度的变化而变化；但在考虑土体自重情况下，拱体跨度s与矢高f均为土体深度z的线性递增函数，这说明了自重应力场的存在对桩间土拱效应起着强化的效果，土体的深度越大，自重对拱效的强化效果就越大.(3) 相对而言，对c值较小的土体，如松散的砂砾类介质，自重应力场对拱体的强化效果会更为显著.

室内离心模型试验可重现重力场的作用，杨明等[15]的离心模拟照片呈现出桩土上部区域拱体的破坏程度明显要大于桩土下部区域拱体的破坏程度，这表明了桩土下部区域较大的惯性力作用对拱体更明显的保护效果，这与本文的分析结论相一致.

尽管土体自重应力场的存在对桩间土拱效应起着强化的效果，土体的深度越大，自重对拱效的强化效果就越大.但另一方面，除土体的平动滑移外，一般来说土体的深度越大，离滑动面处距离越小则土体的侧移就越小；土体的深度越小，离滑动面处距离越大则土体的侧移就越大.土体侧移越大桩间拱效越易充分发挥出来，侧移越小则会抑制桩间拱效的发挥.所以，土体的自重应力与侧移大小这两者综合在一起，起到中和的效果，可缩短不同深度处桩间拱体间尺寸的差距，使桩间拱体间的大小沿深度趋向一致.

5结语

(1) 对桩侧面摩阻力支撑形成的土拱体，桩侧界面粗糙程度的降低对拱体的计算结果影响较大，导致桩间设计净距明显降低，相应增加了桩的数量及加固成本，所以工程中尽可能增加桩侧面的粗糙程度.

(2) 在考虑土体自重情况下，对桩侧面摩阻力支撑形成的拱体，仅在拱脚出现破坏时，本文给出拱体跨度s与矢高f均为土体深度z的线性递增函数，这说明了自重应力场的存在对桩间土拱效应起着明显的加强效果.所以，不考虑土体自身的自重应力场，也就是把土体看成是无重介质，进行桩土拱体模式的设计会过于安全，本文的算例从量化角度进一步验证了这一点.

(3) 本文是在边坡的坡度为零和考虑土体重力场的情况下，对桩土拱体进行研究.对倾斜边坡加固护坡桩工程，也可沿用本文的思路，即首先按照不平衡荷载传递系数法计算出桩侧的设计水平滑坡推力p，其次将土体的自重应力等效为土体的内聚力增量、将土体转化为无重介质，最后在水平滑坡推力p作用下进行无重土坡护坡桩的拱体设计.

(4) 土体的自重应力与侧移大小这两者综合在一起，可缩短不同深度处桩间拱体间尺寸的差距，使桩间拱体间的大小沿深度趋向一致.

参考文献：

[1] RICHARD L H.The arch in soil arching[J].Journal of Geotechnical Engineering,ASCE,1985,111(3)：302-318.

[2] 杨雪强,何世秀,庄心善.土木工程中的成拱效应[J].湖北工学院学报,1994,9(1)：1-7.

YANG X Q,HE S X,ZHUANG X S.On arch effect in civil engineering[J].Journal of Hubei University of Technology,1994,9(1)：1-7.

[3] 贾海莉,王成华,李江洪.关于土拱效应的几个问题[J].西南交通大学学报,2003,38(4)：398-402.

JIA H L,WANG C H,LI J H.Dicussion on some issures in theory of soil arch[J].Journal of Southwest Jiaotong University,2003,38(4)：398-402.

[4] CHEN C Y, MARTINE G E.Soil-structure interaction for landslide stabilizing piles[J].Computers and Geotechnics,2002,29：363-386.

[5] 张建勋,陈福全,简洪钰.被动桩中土拱效应问题的数值分析[J].岩土力学,2004,25(2)：174-179.

ZHANG J X,CHEN F Q,JIAN H Y.Numerical analysis of soil arching effects in passive piles[J].Rock and Soil Mechanics,2004,25(2)：174-179.

[6] 张建华,谢强,张照秀.抗滑桩结构的土拱效应及其数值模拟[J].岩石力学与工程学报,2004,23(4)：699-703.

ZHANG J H,XIE Q,ZHANG Z X.Arching effect of anti-slide pile structure and numerical simulation[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(4)：699-703.

[7] 王成华,陈永波,林立相.抗滑桩间土拱力学特性与最大桩间距分析[J].山地学报,2001,19(6)：556-559.

WANG C H,CHEN Y B,LIN L X.Soil arch mechanical character and suitable space between one another anti-sliding piles[J].Journal of Mountain Science,2001,19(6)：556-559.

[8] 王乾坤.抗滑桩的桩间土拱和临界桩距的探讨[J].武汉理工大学学报,2005,27(8)：64-67.

WANG Q K.Discussion on the arching effect and the critical spacing between adjacent anti-slide piles[J].Journal of Wuhan University of Technology,2005,27(8)：64-67.

[9] 赵明华,陈炳初,刘建华.考虑土拱效应的抗滑桩合理桩间距分析[J].中南公路工程,2006,31(2)：1-4.

ZHAO M H,CHEN B C,LIU J H.Analysis of the spacing between anti-sliding piles considering soil-arch effect[J].Central South Highway Engineering,2006,31(2)：1-4.

[10] 杨雪强,吉小明,张新涛.抗滑桩桩间土拱效应及其土拱模式分析[J].中国公路学报,2014,27(1)：30-37.

YANG X Q,JI X M,ZHANG X T.Analysis of soil arching effect between anti-slide piles and different arch body modes[J].China Journal of Highway and Transport,2014,27(1)：30-37.

[11] 杨雪强,陈桂林.论粘性土转化为无粘性土的物理基础[J].岩土工程技术,1999,47(1)：50-53.

YANG X Q,CHEN G L.On physical base of transformation from cohesive soil into incohesive soil[J].Geotechnical Engineering Technique,1999,47(1)：50-53.

[12] 杨雪强,刘文治,刘祖德，等.武汉原状粉质粘土与共重塑土的试验对比研究(Ⅱ)：剪胀特性分析[J].广东工业大学学报，2013，30(3)：23-29.

YANG X Q, LIU W Z, LIU Z D, et al. A contrastive study of natural remoulded silty clays in Wuhan(Ⅱ): analyses of dilatancy properties[J].Journal of Guangdong University of Technology, 2013,30(3):23-29.

[13] 刘勇健，符纳，陈创鑫，等.三轴冲击荷载作用前后软黏土的微观结构变化研究[J].广东工业大学学报，2015，32(2)：23-27.

LIU Y J, FU N, CHEN C X, et al.Study on microstructure changes of soft clay befone and after triaxial impact load[J]. Journal of Guangdong University of Technology,2015,32(2):23-27.

[14] 陈仲颐,周景星,王洪瑾.土力学[M].北京：清华大学出版社,2007.

[15] 杨明,姚令侃,王广军.抗滑桩宽度与桩间距对桩间土拱效应的影响研究[J].岩土工程学报,2007,29(10)：1477-1482.

YANG M,YAO L K,WANG G J.Study on effect of width and space of anti-slide piled on soil arching between piles[J].Chinese Journal of Geotechnical Engineering,2007,127(10)：1477-1482.

Calculation of Soil Arch Effect in View of Gravity Stress Field

Yang Xue-qiang, Liu Yong-jian, Ji Xiao-ming

(School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Abstract:Anti-slide piles are a main measure to reinforce slope for slope stability engineering, in which soil arch is easily formed between piles. Soil arch supported by adjacent piles is assumed to be horizontal and usually kept in plane strain status in vertical direction. It studies the calculating method of the soil arch supported by side surface friction of piles, which is combined with soil mass gravity. Then the influence of the soil gravity on arch bodies is further investigated in the view of quantity calculation. The research results show that the arch body in soil mass if considered to be weightless,is very safe for design purpose, because the gravity stress of soil mass has an important strengthening effect on the soil arch bodies formed between adjacent piles.

Key words:anti-slide pile; arch effect; equivalent cohesion; gravity stress; pile space

收稿日期:2015- 11- 20

基金项目:中国电力投资集团公司科技项目(2014-028-NFD-KJ-X)

作者简介:杨雪强(1966-)，男，教授，博士，主要研究方向为岩土类材料的强度与变形的基本特性、深基坑、边坡稳定及挡土结构土压力等.E-mail:xqyfls@126.com

doi:10.3969/j.issn.1007- 7162.2016.03.014

中图分类号:U417.1

文献标志码:A

文章编号:1007-7162(2016)03- 0076- 05