有效沟通，有机融合，提升计算能力

□江苏省苏州市吴中区胥口中心小学　庄志勇



有效沟通，有机融合，提升计算能力

□江苏省苏州市吴中区胥口中心小学庄志勇

《义务教育数学课程标准（2011年版）》指出：“数学教学应该注意从学生最感兴趣的事物出发，为他们提供参与数学学习的机会。”因此，在日常教学中我们不能单一地教给学生知识，而是将所学的知识系统化，注重沟通知识之间的内在联系，将新知和原有的知识有机地融合在一起，利用数与形的结合帮助学生建立直观的图形象思维，让学生从不同的角度运用多种方法寻找所要解决问题的核心，进而学生在获取知识的同时，也提升了认识，发展了计算能力。

一、抓准知识原点，沟通内在联系

【片段1】认识比的意义。

谈话引入：一幅图片，有的看起来很漂亮，很美观，有的看起来却很别扭，请看这三幅，哪一幅看起来最美观，最舒服。

师：看来大多数同学都认为是第2幅，不知道大家有没有发现。一幅图片的长和宽不同，给人带来的感觉也就不一样。我们先来观察一下大多数同学认可的第二幅图片，你知道可以怎样表示长和宽之间的关系吗？（长3分米，宽2分米）

生1：长比宽多1分米。

师：你能用算式来表示你的思考过程吗？还可以怎么说？

生1：宽比长少1分米。

师：无论是“长比宽多1分米”，还是“宽比长少1分米”，都可以说成“长和宽相差1分米“，表示的是长和宽的相差关系，用减法计算。还有其他说法来介绍它们之间的关系吗？

师：还有谁想说？

师：这两种说法表示的是长和宽之间的什么关系？用什么方法计算？

生：用除法计算，这两种说法表示的是长和宽之间的相除关系。

师：对于这样的相除关系，还有一种新的表示方法，如长是宽的倍，可以说成长和宽的比是3比2。

板书：

本节课是在学生已经学生了分数、除法相关的知识上进行学习的。通过学生对生活情境的运用，在交流中明确了长和宽之间的不同的表示关系，而其中的相除关系就是学生学习比的前提。将比和除法相沟通起来，利用除法进行引入和理解，让学生在直观中感受除法和比之间的共同之处，自觉地建构起彼此之间的联系。这样使得原本枯燥、抽象的知识变成具体直观，易于学生理解和接受。

二、在对比中融合知识

【片段2】比和除法、分数之间的关系。

请大家观察黑板上求比值的这两道算式，思考，比和除法、分数之间有什么样的关系呢？请同桌之间相互讨论一下。

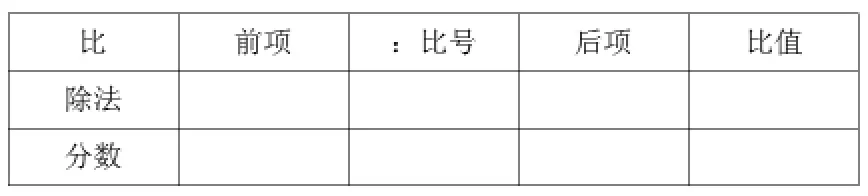
讨论后汇报交流，交流后，同桌协作，将表格填写完整。

这里，学生填好后，选择学生到视频展示台前演示。

师：我们在学习除法时，被除数÷除数=商。其中对哪个数有特别的规定？

生：除数，除数不能为0。

师：那分数呢？

生：分母不能为0。

那，根据比和除法和分数之间的联系，想一想，比需不需要也有些特别的规定呢？

生：比的后项不能为0。

在完善认知结构时，一般要借助必要的学习素材，在已有和现有的知识之间建立起一条纽带，通过观察、比较、交流等多种形式逐步提升认识。从上面的教学片段中可以看出，学生根据黑板上的两组算式进行判断，在对比活动中能够充分暴露学生的思维过程，营造一个交流、争辩的氛围，让思维发生碰撞，对于“比”这个知识有一个清晰的认识，从而深化理解所学知识的核心。

三、数形结合，提升认识

【片段3】“分数的加法和减法”例1。

教师和学生读题分析题以后，学生比较容易地列出了算式，根据学生的回答，老师将算式板书在黑板上。学生尝试计算，组织学生交流结果。

师：请将你的想法和大家分享一下。

生1：分母上的2+4=6，分子上的1+1=2。所以得数是。

师：和他一样想法的同学请举手。（班中有多只手举起）那你们是怎样想的呢？

师：和他不一样想法的同学请举手。（有几个学生的手举起）还有不同的意见，请你来说一说。

学生拿出长方形纸进行操作并展示。

师：请你观察一下，涂色部分共占了这张长方形纸的几分之几？

老师结合图将黑板上的算式完成。

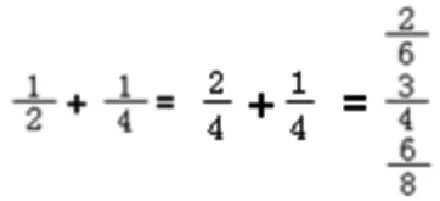
生：经过了一个通分的过程。转化成了同分母分数的加分。

生：转化过后分数单位相同了。

这位老师在整个异分母分数加法的教学中，学生出现了理解上的错误，认为异分母分数的计算方法是分母加分母，分子加分子。而老师没有轻易地判断对错，而是很好地利用了学生建构出来的错例，让学生直观地观察涂色部分占这张长方形纸的几分之几，从而让他们清晰地看出了一个通分的过程。

在我们日常的教学中，学生能否解决相关的题目关键在于能不能找准问题的核心。不过，鉴于学生的年龄特点，他们空间想象的能力比较弱，不能在大脑中投影出清晰的表象，这就导致了学生认知上的偏差。因此，教师利用直观的图形来帮助学生思考，用具体的图形促进学生的思考，数与形的结合沟通了孩子头脑中已有的思维。图形清晰地把几个不同的分数分成相同的分数单位，也就是所有的分数单位都相同了，这样才能进行计算。数与形的结合，提升了学生的认识，他们对知识的理解更加透彻，记得也更加牢固。