基于HHT的露天矿爆破振动信号分析

毛　晖

(福建省天玉方圆矿业有限公司)



基于HHT的露天矿爆破振动信号分析

毛晖

(福建省天玉方圆矿业有限公司)

摘要采用经验模态分解(EMD)提取爆破振动信号的固有模态函数(IMF)分量，对主要成分作Hilbert变换，得到各IMF分量的频率特征；对振动信号进行Hilbert变换，得到信号的Hilbert谱和边际能量谱，从频谱能量的角度分析了爆破振动能量在不同频率段的分布特征。结果表明：爆破能量主要集中在100 Hz以内的低频区域，020 Hz频带能量分布较均匀，2045 Hz能量变化较大，45 Hz以后能量很小。研究结果验证了HHT方法在爆破振动信号分析中的高效性和适应性，HHT方法处理非线性、非平稳的爆破振动信号简单有效，具有很好的推广价值。

关键词露天爆破振动HHTEMDHilbert谱

随着爆破技术在露天及地下采矿、城市道路交通等基础设施建设中的大力开发和应用，爆破施工对周围环境、邻近构(建)筑物的安全影响逐渐受到人们的重视，其中爆破产生的地震效应是最具威胁的危害之一[1-2]。Hilbert-Huang transform(希尔伯特-黄变换，HHT)是由Norden E Huang等人于1998年提出的非平稳信号的非线性非平稳处理方法，是近年来对以傅立叶变换为基础的线性和稳态谱分析的一个重大突破[3]。HHT方法已在爆破振动信号的处理方面取得了大量应用，宗琦等采用HHT方法对煤矿巷道掘进爆破地震波信号的频谱特征和能量分布进行了研究[4]；徐振洋等基于HHT方法研究了露天煤矿台阶爆破地震信号的时频及能量分布特征[5]；张义平等用HHT方法研究了硐室大爆破震动的时频特征及震动传播特性[6]；钱守一等基于HHT瞬时能量分析微差爆破实际延迟时间的识别[7]。本文对露天台阶爆破在近地表轨道运输平硐的爆破地震波信号进行现场监测，并运用HHT方法对爆破振动信号进行经验模态分解的基础上分析各分量的频谱、能量特征。

1爆破振动信号HHT分析方法

爆破振动信号HHT分析方法由EMD(Empirical Mode Decomposition，经验模态分解)和Hilbert变换两部分组成。对信号进行EMD分解，能有效地把各种频率成分以IMF(固有模态函数)的形式从中分离出来,之后对IMF分量进行希尔伯特变换，可得到各种表达方式的Hilbert谱，以便分析振幅和能量随时间和频率的分布情况[8]。

1.1EMD分解原理

EMD是一种由数据驱动的自适应分解方法，可将非平稳信号分解为不同尺度的一系列IMF[9]。EMD分解的过程如下：

(1)计算信号x(t)的所有极值点，分别将所有的局部最大值和最小值用3次样条插值函数求出信号的上、下包络线均值m11(t)。

(2)原信号x(t)减去m11(t)得到分量h11(t)，即

(1)

重复该过程，直到h11(t)成为真正的IMF分量c1(t)，即

(2)

第一个IMF分量c1(t)为原始信号中的最高频率分量。从原信号中分离出c1(t)，得到残余信号r1(t)，即

(3)

(3)r1(t)仍包含原始信号中的频率信息，因此将其作为新的信号重复上述步骤(1)、步骤(2)分解过程，得到第二个分解分量c2(t)，以此类推，即

(4)

(4)当最后得到的残余信号rn(t)的值非常小，小于预定的误差，或为单调函数，即不能再分解出IMF分量时，终止整个分解。原始信号就可表示为

(5)

由于分解过程具有自适应性，因此，分解得到的各个分量经HHT变换后得到的结果能够反映真实的物理过程，可以很好地对非平稳信号进行特征分析。

1.2Hilbert谱分析

对IMF分量进行Hilbert变换，得到每个分量的瞬时频谱，综合所有分量的瞬时频谱即得到Hilbert谱[10-11]。Hilbert谱是幅度在时间频率平面上的分布，可采用颜色编码图、三维空间图形等形式表示。Hilbert谱的表达形式为

(6)

式中，i=1,2,…，n为IMF的个数；Re为实部;ai(t)为幅值;ωi(t)为瞬时频率。

在频域内对Hilbert幅值的平方进行积分，得到Hilbert瞬时能量谱，反映爆破振动过程中信号能量随时间的变化。Hilbert瞬时能量谱的表达形式为

(7)

在时域内对Hilbert幅值的平方进行积分，得到Hilbert边际能量谱，表征振动信号随瞬时频率的相对能量分布。Hilbert边际能量谱的表达形式为

(8)

对ES在频域、IE在时域进行积分可得到信号的能量，2种方法求得的结果是相等的，即

(9)

2工程概况

国内采选规模最大的某金铜矿矿区岩石以坚硬-半坚硬块状岩类为主，局部夹薄层软弱岩石。矿山采用深孔台阶爆破,回采台阶标高为+628 m，台阶高12m，坡面角为75°。台阶爆破的炮孔直径为165mm，超深为1.5 m，孔距为6 m，排距为4 m，采用铵油炸药，连续装药结构，逐孔起爆，使用澳瑞凯高精度雷管，孔内延期与孔外延期相结合，排间微差时间为65 ms，孔间微差时间为25 ms，孔内选用600 ms雷管。

选厂一条轨道运输平硐位于爆区正下方+517 m 标高，距离露天爆区不远，平硐断面为三心拱形，面积为14.28 m2。为了研究露天台阶爆破振动对轨道运输平硐的影响，于2014年8月21日—2015年3月9日在平硐内布置测点进行长期监测。监测设备选用成都中科动态仪器有限公司研制的TC4850型爆破振动监测仪，测试量为质点振动速度和主振频率，同时记录同一测点垂直方向、水平径向、水平切向3个方向的质点振动速度分量。140914炮次的振动数据见图1。

图1　振动速度波形曲线

3爆破振动信号EMD分解

3.1爆破振动信号EMD低通滤波

原始信号经EMD分解后，计算各IMF分量与信号的互相关系数，其中IMF分量1和2与原始信号的互相关系数分别为0.000 5、0.000 9，为明显的噪声分量，采用文献[12]中的低通滤波器去除该噪声分量。把其他分量进行重新组合，得到重构信号，计算重构信号与原信号的互相关系数为0.999 2，表明重构信号与原始信号的相关程度很高，基本上保留了原始信号的信息，EMD低通滤波能有效地实现爆破振动信号去噪。噪声分量与重构信号见图2。

图2　信号去噪与重构

3.2EMD分解与分析

对重构信号进行EMD分解，得到的IMF分量见图3(a)，计算各IMF分量的功率谱密度(PSD)见图3(b)。图3(a)表明：重构信号经EMD分解得到10个分量，其中IMF分量为c1c9，R为余量；其中c3c5的振动幅值较大，是振动信号的主要组成部分，其他IMF分量的振动幅值较小，是振动信号的次要组成部分。图3(b)表明：先后得到的IMF分量的频率越来越小，c1分量的优势频率为180250 Hz，c9分量的优势频率降至5 Hz以内；主要IMF分量c3的优势频率为3040 Hz，c4分量的优势频率为2535 Hz，在33 Hz处PSD最大，c5分量的优势频率为1035 Hz，说明振动信号的优势频率位于1040 Hz。

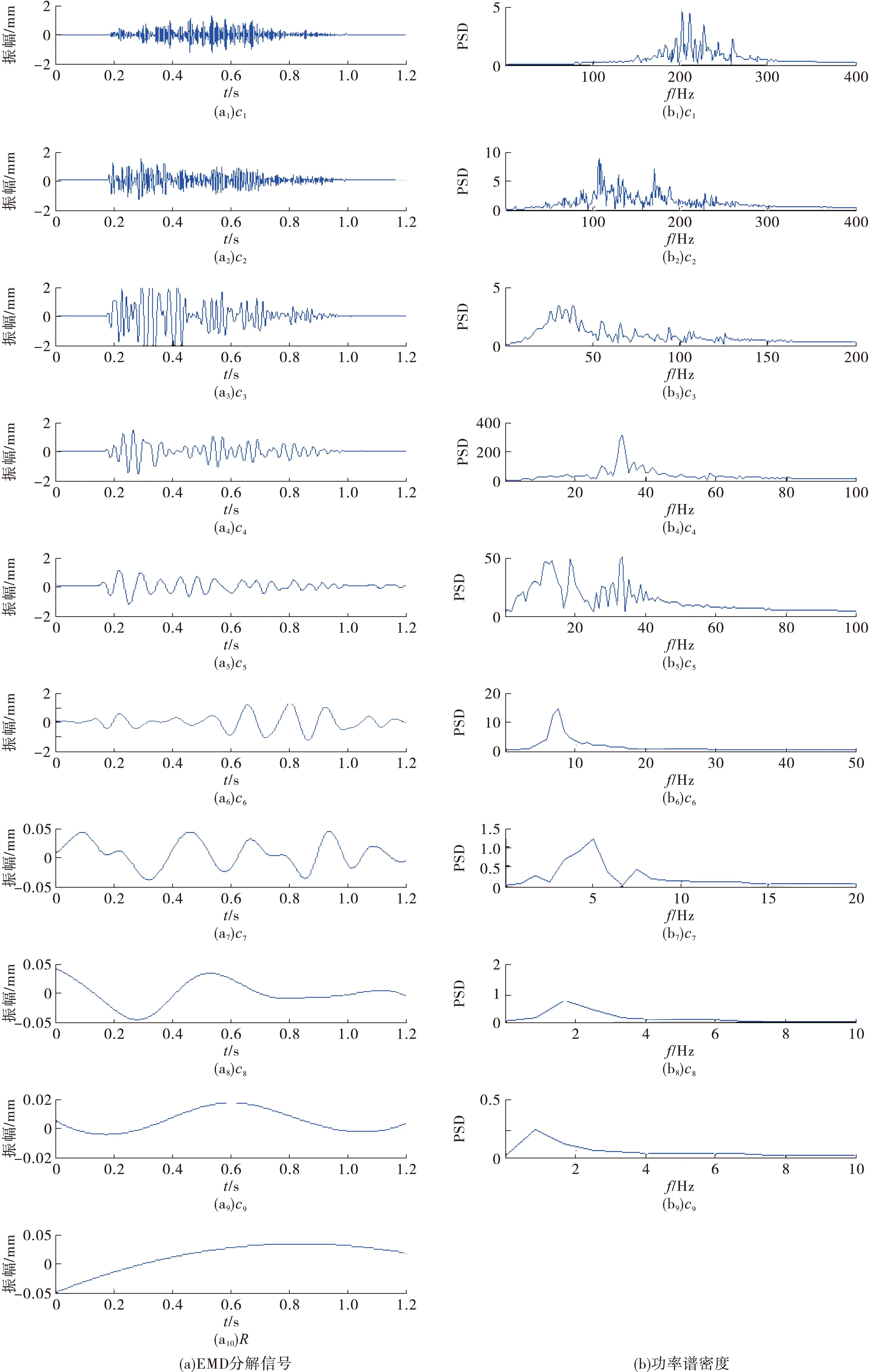
图3　EMD分解和PSD

4爆破振动信号HHT谱分析

图4为爆破振动信号的功率谱密度图，可知，信号能量主要集中在100 Hz的低频范围内，其中020 Hz信号能量随频率增加而缓慢增大，从20 Hz开始信号能量加速增大，并在3035 Hz达到峰值，之后迅速回落，3540 Hz出现二次小峰值，50 Hz以后能量较小，且分布均匀。

图4　爆破振动信号的功率谱

图5为爆破振动信号的Hilbert时频谱，显示了时间、频率、振幅三者的关系。图中左侧的颜色编码棒表示不同振幅的大小，颜色越深说明该时刻、该频率振幅越大。可以看出，在时间轴上振幅主要集中在0.20.4 s，在频率轴上振幅主要集中在50 Hz以内。在时间轴为0.3 s左右、频率轴为33 Hz左右深色点较为集中，说明振动幅值较大。

图5　爆破振动信号Hilbert谱

5结论

(1)在爆破振动现场测试的基础上，通过分析露天爆破地震波的频谱特征和能量分布特性，研究了露天爆破振动对近地表轨道运输平硐的影响，研究成果对类似矿山爆破工程具有一定的指导意义。

(3)HHT方法处理非线性、非平稳的爆破振动信号简单有效，能准确提取时程曲线的主要特征信息，并赋予其物理意义，是爆破振动信号分析的有效工具。

参考文献

[1]史秀志.爆破振动信号时频分析与爆破振动特征参量和危害预测研究[D].长沙:中南大学，2007．

[2]史秀志,周健，崔松,等.露天采矿爆破振动对民房危害预测的DDA模型及应用[J].中南大学学报:自然科学版,2011,42(2):441-448．

[3]Huang N E，Shen Z，Long S R，et a1．The empirical modedecomposition and the Hilben spectrum for nonlinear andnonstationary time series analysis[J]．Proceedings of theRoyal Society of London，Series A，1998(454)：903-995．

[4]宗琦,汪海波,徐颖,等.基于HHT方法的煤矿巷道掘进爆破地震波信号分析[J].振动与冲击,2013,32(15):116-120.

[5]徐振洋,杨军,陈占扬.高精度雷管逐孔起爆地震信号的精确时频分析[J].煤炭学报,2013,38(S2):331-336.

[6]张义平,李夕兵,赵国彦,等.基于HHT方法的硐室大爆破震动分析[J].岩石力学与工程学报,2005,24(S1):4784-4789.

[7]钱守一，李启月．微差爆破实际延迟时间的HHT瞬时能量识别法[J].矿业研究与开发,2012，32(2)：113-116.

[8]李夕兵,凌同华,张义平.爆破振动信号分析理论与技术[M].北京：科学出版社,2009.

[9]张义平,李夕兵,左宇军.爆破振动信号的HHT分析与应用[M].北京：冶金工业出版社,2009.

[10]孙新建.基于Hilbert能量分析的岩体爆破震动损伤研究[D].天津:天津大学,2012．

[11]Battista B M，Knapp C，McGee T.Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data[J].Geophysics,2007，72(2):29-37．

[12]李夕兵，张义平，左宇军，等．岩石爆破振动信号的EMD滤波与消噪[J].中南大学学报:自然科学版,2006,37(1)：150-154.

(收稿日期2016-01-26)

毛晖(1972—)，男，工程师，354012 福建省龙岩市经济技术开发区连圣片区。