基于AHP-FUZZY的某铜钨矿采矿方法优选*

左　蕾　喻　清,2　章求才

(1.南华大学核资源工程学院；2.铀矿冶生物技术国防重点学科实验室)



基于AHP-FUZZY的某铜钨矿采矿方法优选*

左蕾1喻清1,2章求才1

(1.南华大学核资源工程学院；2.铀矿冶生物技术国防重点学科实验室)

摘要采用层次分析法(AHP)与模糊数学(FUZZY)方法对某铜钨矿的采矿方法进行模糊优选。从技术、经济和安全方面选取了影响采矿方法选择的9个主要因素，构建了多目标决策的综合评价指标体系；用层次分析法确定各评价指标的权重；采用模糊数学法处理各采矿方法的定性、定量指标值，分别得到相应类型指标的隶属度；最终计算出3个备选方案的综合优选度分别为80.5%、83.9%和74.7%，从而确定上向进路充填采矿法为最优方案。实践表明,优选方案开采过程中各项指标均达到最优水平，为矿山创造了良好效益；证明了层次分析法和模糊数学法的科学性和可行性。

关键词采矿方法优选评价指标层次分析法模糊数学

采矿方法的选择是矿床开采过程中需要解决的关键问题，是一项具有很强综合性的系统工程[1]，涉及许多只能定性描述的模糊概念、判断、推理等不能确定的内容[2]。因此，要从多个备选采矿方案中优选出一个最佳方案，非常困难。采用传统方法优选采矿方法时，主要依靠经验法和工程类比法，仅能定性地分析相关的影响因素，而不能定量分析[3]，同时不同矿山矿体的赋存条件、矿山的技术经济条件等因素各不相同。因此，采用传统的类比法确定最优采矿方法具有很大的局限性[4-5]。而将层次分析法和模糊数学理论相结合能够以数学形式量化分析相关指标，从各采矿方案的技术、经济、安全方面进行综合评判，最终确定合理的实施方案，使采矿方法的选择更加合理、科学、可靠[6]。

1矿山开采技术条件

某铜钨矿Ⅰ#矿体呈透镜状或扁豆状产出，走向呈南东东—北西西向，近于东西向，倾向南，倾角为70°～80°；矿体地表出露厚度为7.26～11.35 m，平均厚9.1 m；矿体全长约160 m，所含矿种主要是黄铜矿，共生矿为白钨矿，整个矿体平均含铜0.802%，平均含钨0.315%；矿体产于花岗岩中，顶底板及围岩具有较好的稳固性，但矿体赋存在破碎带中，风化程度较深，硬度小，稳固性差，且厚度较大，工程地质条件中等。矿坑水主要来源于裂隙带中极小量的裂隙水和流量很小的地表水，其对开采影响甚小，水文地质条件简单。

2采矿方法初选

根据该铜钨矿Ⅰ#矿体赋存情况和开采技术条件，并参考国内外类似矿山的采矿方法，经综合分析，提出了3种技术上可行的采矿方法，即下向水平分层充填采矿法(方案Ⅰ)、上向进路充填采矿法(方案Ⅱ)、浅孔留矿采矿法(方案Ⅲ)。

根据以上提出的备选采矿方法，并结合主要的技术、经济及安全指标，可得到表1中各备选采矿方案对应的评价指标。各评价指标的参数通过咨询专家、调查研究、计算及选用类似矿山的指标得到。

3采矿方法优选

3.1层次分析法专家权重原理

层次分析法(AHP)是一种定性和定量相结合、系统化、层次化的分析方法[7]。它先把多目标决策的问题按隶属关系的高低有序排列成目标层(T)、准则层(C)及指标层(I)的总分层次结构，再根据对一定实际情况的判断，确定同层次因素的相对重要性，并进行量化[8]。

根据表2的比较标准，分别比较影响采矿方案选择的9个主要指标，构造判断矩阵D：

表1　各方案的综合评价指标体系

在得到的判断矩阵D的基础上，采用根法，由公式Dw=λmaxw，计算得到最大特征根λmax，其中归一化得到的w，即作为相应指标的权重向量。

判断矩阵D中的指标按行依次相乘，得到各行指标乘积：

(1)

计算Mi的n次方根：

(2)

(3)

计算判断矩阵D的最大特征根：

(4)

式中，向量w=(w1，w2，…，wi)T;式(1)～式(4)中i=1，2，…，n，n=9。

为避免判断矩阵D的主观性、片面性，进行一致性检验：

CR=CI/RI ,

(5)

(6)

式中，CI为一致性检验指标；n为判断矩阵的阶数；RI为平均随机一致性指标，取值见表3。

表3　平均随机一致性指标取值

当CR<0.1时，矩阵D的一致性才是可接受的，否则，要重新调整判断矩阵D，再按根法的步骤计算，直至满足一致性检验。

3.2专家权重值的计算

根据表1给出的3种备选采矿方案的综合评价指标体系，并结合式(1)建立T-C的判断矩阵D1和C-I的判断矩阵D2：

由式(1)～式(4)，求解得专家权重向量w1=(0.540，0.297，0.163),w2=(0.204，0.130，0.136，0.071，0.286，0.027，0.067，0.037，0.043),再对判断矩阵D1和D2进行一致性检验，求解得到最大特征根λ1max=3.01，CR1=0.009 6<0.1,满足一致性的要求，可被接受；λ2max=10.137，CR2=0.097<0.1，满足一致性的要求，可被接受。

3.3模糊数学确定隶属度原理

定量指标的隶属度由隶属函数法确定[9-10]，对于正指标(收益性指标)，越大越优，即

(7)

对于负指标(消耗性指标)，越小越好，则

(8)

式中,rij为j方案的量化评价指标i的相对隶属度；xij为j方案的评价指标i的评价量化值。

则得到目标相对隶属度矩阵A：

其中,i=1，2，3，…,n；j=1，2，3，…,n。

定性指标的相对隶属度采用等级评定法确定[11]，按表4所示的九级赋值标准给出其隶属度rij的评定值。

表4　定性指标赋值

3.4隶属度矩阵的计算

根据表1给出的3种采矿方案的综合评价指标，建立评价矩阵P：

定量指标的相对隶属度根据式(7)和式(8)确定，定性指标的相对隶属度则根据表4确定，最终得到相对隶属度矩阵H：

3.5采矿方法排序

由得到的权重向量w2和隶属度矩阵H，根据公式

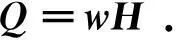
(9)

计算得出Q=(0.805，0.839，0.747)。

因此，3种备选方案的综合优选度：方案Ⅰ为80.5%；方案Ⅱ为83.9%；方案Ⅲ为74.7%。由最大隶属原则，Q值越大的方案，选择的可能性越高。故方案的优选顺序为方案Ⅱ>方案Ⅰ>方案Ⅲ，方案Ⅱ(上向进路充填采矿法)为最优。

该矿山经过实践表明，上向进路充填采矿法经济合理、技术可行、安全可靠，取得了良好的效果。

4结论

(1)在采矿方法的经济、技术以及安全层面上，综合考虑各影响因素，引入定性与定量指标，以采矿方法最优为目标，构建了多目标决策的综合评价指标体系。综合分析表明：采场生产能力、采充总成本为主要影响指标，其次为损失率、贫化率。

(2)生产实践表明，模糊优选得到的上向进路充填采矿法(方案Ⅱ)在该铜钨矿山具有很好的操作性、实施性。采矿过程中的各项指标均达到最优水平，为矿山创造了良好的效益，达到了优选采矿方法的目的。

(3)将层次分析法与模糊数学相结合，确定了评价体系中各指标的权重以及相对隶属度，避免了传统评价方法的片面性与局限性，为确定多目标决策提供了一条科学、简便、高效的途径。

参考文献

[1]葛文杰．利用模糊数学法对采矿方法进行综合评判和选择[J]．矿业工程，2012，10(3)：14-17．

[2]赵彬，王新民，张钦礼．新桥硫铁矿采矿方法模糊选择[J]．安徽理工大学学报：自然科学版，2008，28(4)：21-25．

[3]李真，褚洪涛．基于模糊数学的柿竹园矿采矿方法优选[J]．矿业研究与开发，2015，35(8)：5-8．

[4]刘玉龙，丁德馨，李广悦，等.层次分析法在铀矿山采矿方法优化选择中的应用[J].矿业研究与开发，2011，31(6)：8-10,112．

[5]谭忠银，匡正平，邱慧远．层次分析法在铀矿山采矿方法优化选择中的应用[C]∥中国核科学技术进展报告(第三卷)——中国核学会2013年学术年会论文集第2册(铀矿冶分卷、核能动力分卷(上))．北京：中国核学会，2013：6．

[6]李凤义，聂文波，陈维新，等．模糊数学在充填开采方法中的应用[J]．采矿技术，2014，14(1)：21-23．

[7]李雅阁．基于系统聚类的层次分析法对采矿方法影响因素分析及方案优选[J]．黄金，2015，36(11)：28-31．

[8]杜坤，李夕兵，周健，等．采矿方案优选的熵模糊物元决策模型[J]．矿冶工程，2010，30(5)：12-17．

[9]赵国彦，栗红玉，赵晓昕．新城金矿厚大破碎矿体采矿方法的模糊优化[J]．矿业研究与开发，2011，31(3)：7-10．

[10]王泽江，李秦，郭元，等．模糊数学和数值模拟在优选某铀矿矿体方案中的应用[J]．铀矿冶，2015，34(3)：157-160．

[11]聂兴信，李宗利，温申文，等．基于多目标模糊决策的二里河铅锌矿采矿方法优选[J]．金属矿山，2010(2)：22-25，29.

(收稿日期2016-02-23)

国家自然科学基金重点项目(编号:U1401231)；国家自然科学基金项目(编号:11505093，51574152)；湖南省教育厅资助项目(编号:13C800)；衡阳市科技局资助项目(编号:2013KS31)；南华大学创新训练中心“大学生研究性学习和创新性实验计划”项目(编号:201412,201422,201501)；南华大学“铀矿山岩土工程灾害预测与控制”创新团队项目(编号：NHCXTD04)。

左蕾(1994—)，男，421001 湖南省衡阳市蒸湘区常胜西路28号。