永磁直线同步电机的自适应滤波迭代学习控制*
赵希梅,马志军,朱国昕
(沈阳工业大学 电气工程学院,沈阳 110870)
永磁直线同步电机的自适应滤波迭代学习控制*
赵希梅,马志军,朱国昕
(沈阳工业大学 电气工程学院,沈阳110870)
摘要:针对永磁直线同步电机(PMLSM)迭代学习控制(ILC)过程中非重复性扰动放大的问题,提出一种自适应滤波ILC方案。该控制方案由一个直接反馈环和一个附加的ILC回路组成。在ILC回路上设计开环PD型学习律,与反馈控制器相结合使伺服系统快速收敛,并保证系统具有较高的控制精度。依据伪Wigner-Ville分布获得的信号时频分布信息,设计带宽沿时间轴变化的自适应滤波器Q,避免了在迭代学习过程中非重复性扰动的放大。实验结果表明,所提出的控制方案在提高位置跟踪精度的同时,有效地增强了系统的鲁棒性。
关键词:永磁直线同步电机;迭代学习控制;自适应滤波器;鲁棒性;跟踪精度
0引言
PMLSM与传统“旋转电机+滚珠丝杠”的驱动方式相比,采用了直接驱动方式,中间不需要任何的转换环节,具有推力大、损耗低、响应速度快、电气时间常数小等优点,被广泛应用于高速与高精度数控、精密仪器、电子制造装备等领域[1-2]。电机运行时,摩擦力、端部效应等重复性扰动和参数摄动、测量波动等非重复性扰动毫无衰减地反映到电机动子及控制器上,增加了伺服控制难度,因此提高了对控制器设计的要求[3-4]。
对于重复运行的伺服系统,ILC理论上可以获得完全跟踪,但系统存在非重复性扰动时,在迭代轴上会无限放大扰动,在这种情况下,系统的鲁棒性成为迭代ILC中的一个难题[5]。文献[6]设计一种基于自适应ILC的PMLSM伺服系统,加快了收敛速度,但没考虑系统中的非重复性扰动。文献[7]利用P型ILC对PMLSM伺服系统进行位置误差补偿,由于滤波器设计简单,很难有效地抑制测量噪声。文献[8]在ILC中加入自适应滤波器Q抑制噪声,但学习滤波器的设计严重依赖系统模型,当系统参数变化或建模存在误差时控制效果不佳。
针对上述问题,本文提出一种自适应滤波ILC方案。控制系统由反馈环和ILC回路组成,ILC与反馈控制器相结合保证了系统的跟踪精度,自适应滤波器Q限制了扰动的放大、提高了系统的鲁棒性。最后通过实验表明了所提出的控制方案是有效可行的。
1PMLSM数学模型
在磁场定向矢量控制条件下(id=0),对PMLSM进行矢量控制,则PMLSM电磁推力方程为:
(1)
PMLSM机械运动方程为:
(2)
(3)
Fripple=fslot+fend=A1sin(2πy/τ)+A2cos(2πy/τ+θ)
(4)
其中,Fripple为推力脉动,fslot为齿槽力,fend为端部效应,A1为齿槽力波动的幅值,A2为端部效应力波动的幅值,θ为初始相位电角度。
2伺服系统设计
2.1PMLSM自适应滤波迭代学习控制系统
PMLSM自适应滤波迭代学习控制系统框图如图1所示。ILC为迭代学习控制器,L与vk构成PD学习律,Q为自适应低通滤波器。P为被控对象PMLSM,yd为期望位置,yk+1为第k+1次迭代的输出位置,ek+1为第k+1次迭代的位置误差,uk+1为第k+1次迭代的控制信号,lk+1为被时域分析的信号,ηk+1为第k+1次迭代的测量扰动。C为PD反馈控制器,保证系统的稳定性、提高控制精度。
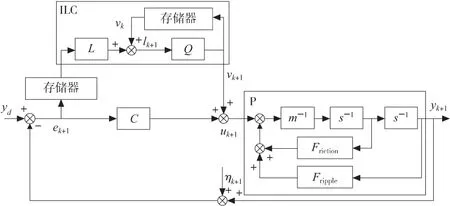
图1 PMLSM自适应滤波迭代学习控制系统框图
由图1可以看出:
uk+1=Cek+1+vk+1
(5)
vk+1=Q(vk+Lek)
(6)
则ILC收敛的充分条件为[9]:
(7)
其中,P1=PS,并且灵敏度函数S1/(1+CP)。P型ILC的收敛速度快,但控制精度不高,D型ILC可达到较高的控制精度,但收敛速度比较慢[10]。因此本文采用开环PD型学习律,设计如下:
(8)
当系数K1和K2确定后,L实际上为一个PD控制器[11]。若选择适当的参数K1、K2使L满足式(7)则系统收敛。
2.2时频分析
设计自适应滤波器Q之前需要利用伪Wigner-Ville分布对信号时频分析,它有很高的时频分辨率,并且减少了Wigner-Ville分布的交叉项,伪Wigner-Ville分布的定义为:
(9)
其中t,ω∈R,s*是所分析的时间信号s的复共轭,ω是单位为赫兹的频率,h(τ)是实的偶窗函数,并且h(0)=0。
为了模仿直线电机启动与停止时的推力状态,选择图2中的曲线作为PMLSM的期望位置和加速度。图3为对图2中的期望位置跟踪时系统运行1次后误差的伪Wigner-Ville分布图,可以看出有用的高频误差信号主要集中在零点附近和加速度变化的时间段,因此该时间段滤波器Q的带宽应较大,以利用更多有用的信息,其它时间段滤波器Q的带宽应较小,过滤更多噪声。
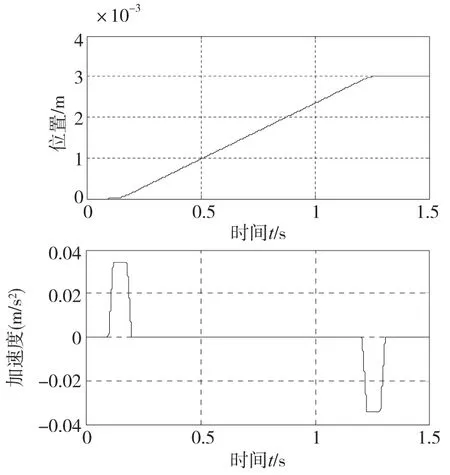
图2 PMLSM的期望位置和加速度曲线
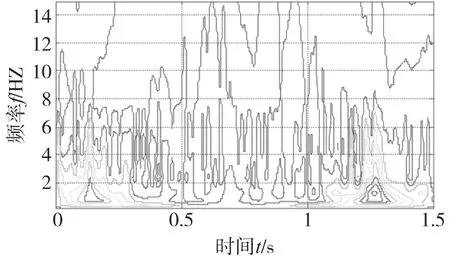
图3 PMLSM运行1次后误差信号的伪Wigner-Ville分布
2.3自适应滤波器Q设计
迭代5次后观察信号lk+1的伪Wigner-Ville分布的三维图可发现高频时间段噪声的能量被放大,把Ce作为低频可用信号与噪声信号的分界点,则迭代k次时,能量超过Ce的频率包络Fmax(t)为:
(10)
其中W()是第k次迭代时信号lk的伪Wigner-Ville分布,把Fmax(t)作为带宽Ω(t)自适应更新律的增益,用δNk(t)评估自适应滤波器带宽变化对误差带来的影响,即:
δNk(t)=Nk(t)-Nk-1(t)
(11)
其中:
(12)
T为时间宽,设计带宽Ω(t)的更新律为:
Ωk+1(t)=Ωk(t)+δΩk(t)
(13)
δΩk(t)=Fmax,k(t)·K·Kk(t)
(14)
其中:
Kk(t)=δNk(t)·(-sgn(δΩk-1(t)))
(15)
初始带宽Ω0要尽可能小,为了避免因带宽变化太快引起的控制性能下降,带宽使用前使用中值滤波器对其进行平滑处理。
3实验与分析
基于DSP的PMLSM控制系统原理框图如图4所示,本实验采用TMS320LF2407A DSP为核心控制单元,驱动电路采用IPM,动子电流检测单元采用霍尔传感器,位置、速度检测采用直线光栅尺。PMLSM采用派克公司的110-2,参数为:R=1Ω,L=8.5 mH,M=0.66 kg,B=0.2 N·s/m,τ=60.96 mm,p=4,Ψf=0.16 Wb。
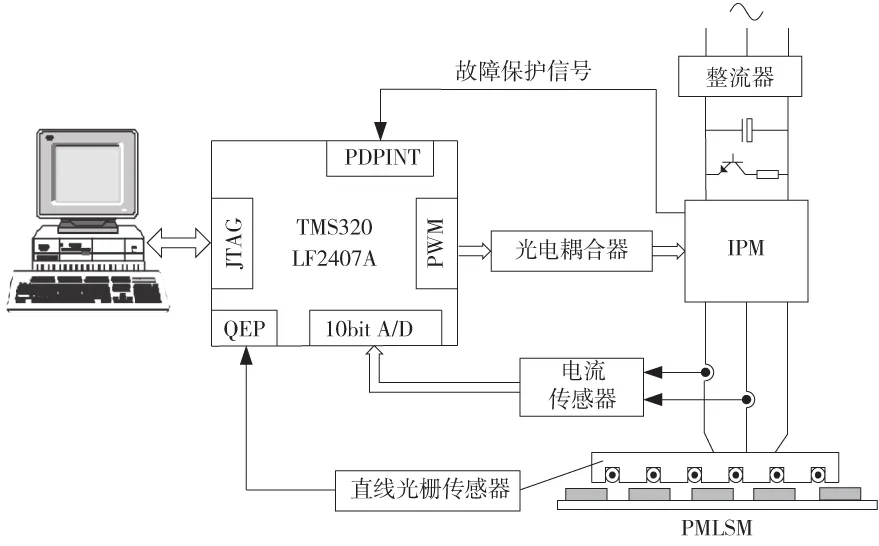
图4 基于DSP的PMLSM控制系统原理框图
PD型ILC和自适应滤波ILC对图2中的期望位置跟踪,两者的反馈控制器C相同,参数为Kp=12000、Kd=110。PD型ILC学习律的参数选择为K1=1750、K2=0.03。由于电机重复误差信号集中在20Hz以下,自适应滤波ILC中Q的参数选择为Ω0=20Hz、K=1×1013、T=0.008,由于Q可以抑制扰动,学习律的参数K1可以选择为较大值,即K1=2550、K2=0.03。PD型ILC迭代15次后的位置误差曲线如图5所示,最大误差为18.9μm。图6为自适应滤波ILC迭代15次后的位置误差曲线,由于摩擦力等的影响,可看出初始位置误差较大,为7.8μm,零时刻以后的最大误差为6.5μm。经对比可知,自适应滤波ILC零时刻以后的最大位置误差减小了约2/3。图7为迭代15次后Q的最终带宽,可看到带宽的变化达到了预期的效果。
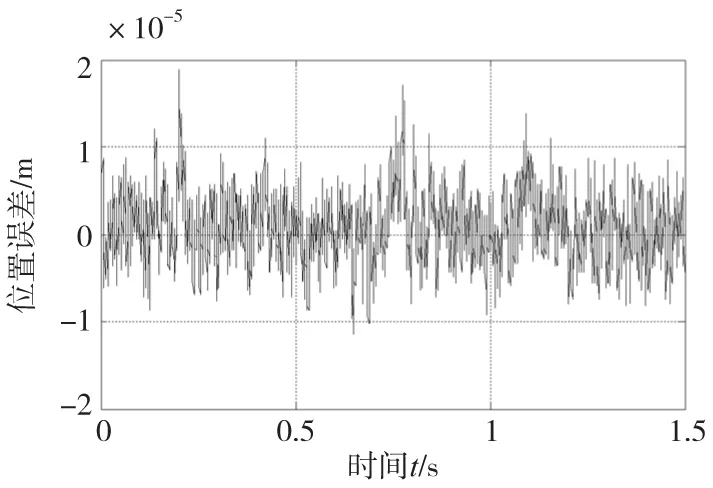
图5 基于PD型ILC的PMLSM位置跟踪误差曲线
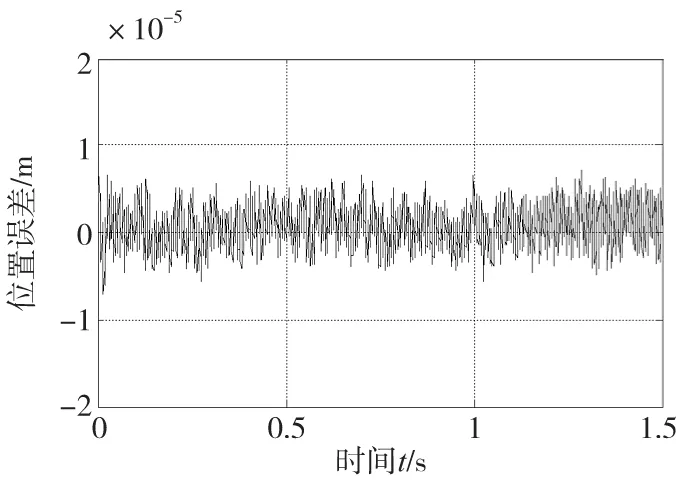
图6 基于自适应滤波ILC的PMLSM位置跟踪误差曲线
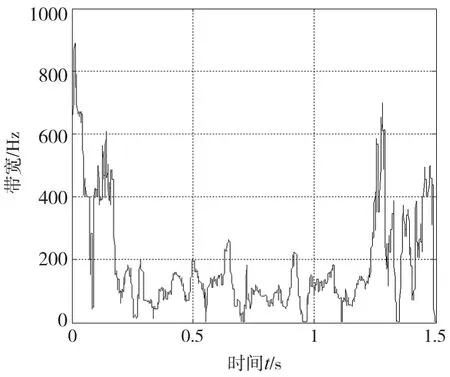
图7 自适应滤波器Q的最终带宽
4结论
本文针对PMLSM伺服系统迭代学习控制过程中放大非重复性扰动问题,提出了自适应滤波ILC方案。PD型ILC与反馈控制相结合保证了系统收敛性及跟踪精度。加入的自适应滤波器Q的带宽在时间轴上根据误差的特征智能变化,尽可能的保留有用输入信息的同时抑制扰动。实验研究表明,自适应滤波ILC有效地抑制了扰动沿迭代轴的放大,与 PD型ILC相比,减小了位置误差,提高了系统的鲁棒性。
[参考文献]
[1] 赵希梅,马志军,朱国昕. 永磁直线同步电动机自适应PD型迭代学习控制[J]. 沈阳工业大学学报,2016,38(1):7-12
[2] 武志涛,李福云. 基于H∞扰动补偿器的永磁直线电机伺服控制器设计[J]. 组合机床与自动化加工技术,2015(11):67-70.
[3] 张宏伟,余发山,卜旭辉,等. 基于鲁棒迭代学习的永磁直线电机控制[J]. 电机与控制学报,2012,16(6):81-86.
[4] 杨俊友,师光洲,白殿春. 基于迭代学习的永磁直线伺服系统扰动抑制[J]. 组合机床与自动化加工技术,2014(8):59-66.
[5] 于少娟,齐向东,吴聚华. 迭代学习控制理论及应用[M]. 北京:机械工业出版社,2005.
[6] 宋亦旭,王春洪,尹文生,等. 永磁直线同步电动机的自适应学习控制[J]. 中国电机工程学报,2005,25(20):151-156.
[7] Teo C S,Tan K K,Lim S Y. Dynamic geometric compensation for gantry stage using iterative learning control[J]. IEEE Transactions on Instrumentation and Measurement,2008,57(2):413-419.
[8] Rotariu I,Steinbuch M,Ellenbroek R. Adaptive iterative learning control for high precision motion systems[J]. IEEE Transactions on Control System Technology,2008,16(5):1075-1082.
[9] 杨俊友,刘永恒,白殿春,等. 基于迭代学习与小波滤波器的永磁直线伺服系统扰动抑制[J]. 电工技术学报,2013,28(3):87-92.
[10] Butcher M, Karimi A, Longchamp R. A statistical analysis of certain iterative learning control algorithms [J]. International Journal of Control,2008,81(1):156-166.
[11] Madady A. An extend PID type iterative learning control[J]. International Journal of Control,Automation,and Systems,2013,11(3):70-481.
(编辑赵蓉)
Adaptive Filtering Iterative Learning Control for Permanent Magnet Linear Synchronous Motor
ZHAO Xi-mei, MA Zhi-jun, ZHU Guo-xin
(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)
Abstract:An adaptive filtering iterative learning control(ILC) scheme was proposed for the non-repetitive disturbances amplification in ILC for permanent magnet linear synchronous motor(PMLSM). The control scheme is composed of a direct feedback loop and an additional ILC loop. The servo system gets fast convergence and has a high control precision by combining the design of open loop PD type learning law on the ILC circuit with the feedback controller. The design of bandwidth in the time axis variation of adaptive filter Q according to the signal time-frequency distribution information from pseudo Wigner-Ville distribution, avoid the amplification of non-repetitive disturbances in the iterative learning process. The experimental results indicate that the proposed control scheme improve the position tracking precision at the same time, effectively enhances the robustness of the system.
Key words:permanent magnet linear synchronous motor; iterative learning control; adaptive filter; robustness; tracking accuracy
文章编号:1001-2265(2016)05-0107-03
DOI:10.13462/j.cnki.mmtamt.2016.05.029
收稿日期:2015-07-10
*基金项目:国家自然科学基金(51175349);辽宁省教育厅科学技术研究项目(L2013060)
作者简介:赵希梅(1979—),女,吉林德惠人,沈阳工业大学副教授,博士,研究领域为直线伺服,数控技术,鲁棒控制,(E-mail)zhaoxm_sut@163.com。
中图分类号:TH166;TG659
文献标识码:A

