一个有限渐近拟非扩张映射族的收敛定理*

陈　明

(遵义师范学院 数学与计算科学学院，贵州 遵义 563002)



一个有限渐近拟非扩张映射族的收敛定理*

陈明

(遵义师范学院 数学与计算科学学院，贵州 遵义 563002)

摘要:在一致凸的Banach空间中, 研究有限渐近拟非扩张映射族的Mann迭代和多步Ishikawa型迭代序列的收敛性, 并对一些已有的Mann迭代和多步Ishikawa型迭代序列进行进一步地推广和统一. 在实数空间中, 构造一个非负实序列,使得这个非负实序列是收敛的, 从而利用这个非负实序列的收敛性证明该迭代序列在一定条件下强收敛到有限渐近拟非扩张映射族的公共不动点.

关键词:Banach空间； 渐近非扩张映射； 渐近拟非扩张映射； Ishikawa型迭代序列

1引言

设K为Banach空间E的非空闭凸子集, T是 K上的一个自映射, F(T)为T的不动点集, 且F(T)≠Ø.

定义 1[1]映射T被称为

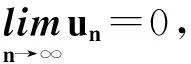
在文献[1-8]中,都在研究众所周知的Mann迭代[3]xn+1=(1-αn)xn+αnTxn和修改后的Mann迭代[3]xn+1=(1-αn)xn+αnTnxn, n≥1.

文献[14]研究了多步Ishikawa型迭代序列的收敛性，如式(1)

(1)

(2)

显然, 当式(2)中 qi≡0和 Ti≡ T时, 即可以得到(1). 因此, 由(2)定义的序列 {xn}是文献[14]中由式(1)定义的序列 {xn}的推广.

在适当的假设下, 本文证明了由(2)定义的序列{xn}强收敛到有限渐近拟非扩张映射族的公共不动点, 其结果对一些学者所研究的Mann迭代和多步 Ishikawa型迭代序列进行了统一和推广[2,9-10,14].

2主要结果

引理 2[9]设p>1,r>0是两个固定常数,E是Banach空间，则E是一致凸的当且仅当存在一个连续的强增的凸函数g∶[0, ∞)→ [0, ∞),g(0)=0，使得对任意的x,y∈Br(0)={x∈E:‖x‖≤r}, 且λ∈[0,1], 有 ‖λx+(1-λ)y‖p≤λ‖x‖p+(1-λ)‖y‖p-ωp(λ)g(‖x-y‖) 成立, 其中ωp(λ)=λ(1-λ)p+(1-λ)λp.

引理 3设 {an}, {tn}和{ln} 3个非负实序列满足条件

(3)

由式(3)有an+1≤tnan+lnan-q≤tnbn+lnbn≤(tn+ln) bn≤(1+cn)bn, n=q+1, q+2, …, 因此

现设 a>0, 如果序列{an}不收敛于a.由{bn} 的定义知, 对任意的n∈ N,有an0,对任意的j>0, 存在nj>j使得

(4)

(5)

由式(4)可知, 存在n0≥ Nε+2q+1(n0-q>Nε+q+1 ), 使得

(6)

由式(3), 式(5)和式(6)可知

(7)

进一步, 由式(7)推出

因此，可以证明

(8)

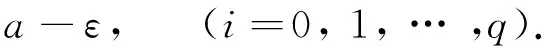
对任意的i=1,2,…,m-2, 由式(2)知

(9)

对 i=m-1, 有

(10)

由式(2)，式(9)和式(10)可得

(11)

由式(9)和式(10)知, 对任意的i=1,2,…,m-1, 有

另一方面, 由式(11)知

(12)

当i= 1,2, …, m-2时, 有

(13)

当i= m-1时, 有

(14)

由式(12)可得

(15)

(16)

当i= 1, 2,…, m-2时, 可推出

综上所述, 当 i= 1,2,…, m-1, 推出

故

当 i=1, 2, …, m, 有

(17)

故当 i= 1,2,…,m时, 有

这表明

因此, {xn}是Cauchy序列. 又因为E是完备的, 从而{xn}在E中是收敛的.

若在定理1中取m=1, qi≡0和Tin≡ T, 将得到迭代序列(1)在渐近拟非扩张映射下的收敛定理.

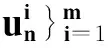
参考文献:

[1] Goebel K, Kirk W A. A fixed point theorem for asymptotically nonexpansive mappings[J]. Proc. Amer. Math. Soc., 1972, 35: 171-174.

[2] Chidume C E, Shahzad N. Strong convergence of an implicit iteration process for a finite family of nonexpansive mappings[J]. Nonlinear Anal. 2005, 62: 1149-1156.

[3] Chidume C E, Ali B. Weak and strong convergence theorems for finite families of asymptotically nonexpansive mappings in Banach spaces[J]. J. Math. Anal. Appl., 2007, 330: 377-387.

[4] Sun Z H. Strong convergence of an implicit iteration process for afinite family of asymptotically quasi-nonexpansive mappings[J]. J. Math. Anal. Appl., 2003,286: 351-358.

[5] Schu J. Weak and strong convergence to fixed points of asymptoticallynonexpansive mappings[J]. Bull. Austral. Math. Soc., 1991, 43: 153-159.

[6] Khan A R, Domlo A A. H. Fukhar-ud-din, Commom fixed points Noor iteration for a finite family of asymptotically quasi-nonexpansive mappings in Banach spaces[J]. J. Math. Anal. Appl., 2008, 341: 1-11.

[7] Hao Y, Wang X, Tong A. Weak and strong convergence theorems for two finite families of asymptotically nonexpansive mappings in Banch spaces[J]. Adv. Fixed Point Theory, 2012, 2(4): 417-432.

[8] Tian Y X. Convergence of ishikawa type iterative scheme for asymptotically quasi-nonexpansive mappings[J]. Comput. Math. Appl., 2005, 49: 1905-1912.

[9] Chidume C E, Li J L, Udomene A. Convergence of paths and approximation of fixed points ofasymptotically nonexpansive mappings[J]. Proc. Amer. Math. Soc., 2005, 133: 473-480.

[10]SuantaiS.WeakandstrongconvergencecriteriaofNooriterationsforasymptoticallynonexpansivemappings[J].J.Math.Anal.Appl., 2005, 311： 506-517.

[11]RashwanRA,AlbaqeriDM.Approximatingcommonrandomfixedpointfortwofinitefamiliesofasymptoticallynonexpansiverandommappings[J].J.oftheEgyptianMathematicalSociety, 2014, 22(2)： 182-189.

[12]LiuQH.Iterativesequenceforasymptoticallyquasi-nonexpansivemappings[J].J.Math.Anal.Appl., 2001, 259： 1-7.

[13]KirkWA.Krasnoselsklii’siterationprocessinhyperbolicspace[J].Numer.Funct.Anal.Optim., 1982, 4： 371-381.

[14]RhoadesBE,SoltuzSM.TheequivalencebetweenMann-Ishikawaiterationsandmulti-stepiteration[J].NonlinearAnal, 2004, 58： 219-228.

Convergence Theorem for a Finite Family of Asymptotically Nonexpansive Mappings

CHEN Ming

(School of Mathematics and Computational Science, Zunyi Normal College, Zunyi 563002, China)

Abstract:Finite asymptotically nonexpansive Mann iterative and multi-step Ishikawa type iterative sequence of convergentare are investigated in the uniformly convex Banach space, and some Mann iterations and multi-step Ishikawa type iterative sequences are popularized. In the real space, a convergent non-negative real sequence is constructed, and it’s convergent. Under certain conditions, the iterative sequence is proved that it converges strongly to the common fixed point of a finite family of asymptotically nonexpansive mappings.

Key words:Banach space; asymptotically nonexpansive mapping; asymptotically quasi-nonexpansive mapping; Ishikawa type iterative

文章编号:1673-3193(2016)02-0104-05

*收稿日期:2015-08-02

基金项目：贵州省科技厅自然科学基金(No.LKZS[2011]2117, No.LKZS[2012]11, No.LKZS[2012]12)

作者简介：陈明(1961-)，男，副教授，主要从事函数论及概率论方面的研究.

中图分类号:O173

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.02.002