偏振光谱BRDF建模与仿真

凌晋江，李 钢，张仁斌，汤 倩，叶 秋

合肥工业大学计算机与信息学院，安徽 合肥 230009

偏振光谱BRDF建模与仿真

凌晋江，李 钢，张仁斌，汤 倩，叶 秋

合肥工业大学计算机与信息学院，安徽 合肥 230009

在偏振光条件下，物体的表面反射受到折射率、表面粗糙度、入射角等多种因素的影响。针对粗糙物体表面在不同波段光照下表现出不同的偏振反射特性，提出一种基于Kirchhof理论的偏振光谱BRDF模型。利用已知材质在不同波长下的复折射率，对其折射率和消光系数部分分别反演出的对应光谱模型，进而得到复折射率的光谱模型；同借鉴经典的表面粗糙度测量方法，结合菲涅耳反射公式，推导出表面粗糙度的光谱模型，将得到的复折射率和粗糙度光谱模型与BRDF模型相结合，推导出偏振光谱BRDF建模。模型分别在折射率随波长变化、粗糙度为常量，折射率、粗糙度均随波长变化以及原模型三种情况下进行仿真对比实验，并将所得到的数据与其他资料进行对比。其结果表明，该模型能够较为准确的反映物体表面的偏振反射特性，并且能够描述偏振度随波长变化趋势的光谱特征，能够为偏振遥感、物质分类等方面的应用提供可靠依据。

偏振光谱双向反射分布函数；折射率；表面粗糙度

引 言

在自然光条件下，目标隐藏主要依靠采用与背景色相近的同色同谱方式进行伪装，由于物体表面的反射光与环境光相近，因此很难发现目标。然而在偏振光条件下，物体表面的反射特性受到其介电系数、粗糙度等多种因素[1]的影响而产生较大的区别，尤其是人造目标相对于自然目标有较强的偏振特性，所以偏振光对人造目标的探测效果尤其明显。同非偏振探测相比, 偏振探测能够提供更多区分目标的特征信息, 而且不需要很高的辐射量测量精度就可以达到相对较高的精度。并且在不同的探测波段下的同一实体目标的反射偏振特性亦有不同。

偏振双向反射分布函数BRDF (pBRDF)是双向反射分布函数(BRDF)的一般表现形式，通过使用矢量的形式描述偏振光，使得pBRDF能够描述物体表面的偏振反射特性。然而现有的各种pBRDF模型多是针对可见光范围内的偏振反射特性，并没有将波长这一因素纳入模型的考虑范围中[2，3]，使得模型本身有很大的局限性，不能适用于红外波段等非可见光波段范围内的光反射特性。另一些模型中，虽然将波长作为模型的参数之一[4]，然而却忽略了模型中其他参量也是随波长而发生变化，如物体的折射率会随着入射光波长的变化而发生改变，表面粗糙度的在特定波长下进行测量，当波长发生变化时，粗糙度也会有所不同。

随着遥感等技术的发展，偏振光谱等技术广泛应用于物质分类等领域。然而从上述讨论中可以看出现有pBRDF模型很少将波长纳入其考虑因素，并且其他参量也是用常数进行表示，并没有与波长相关进行建模。因此，现有的各种模型无法满足人们对于偏振光谱信息的需求。本文针对上述问题，将波长作为参考因素加入pBRDF模型中，并着研究重对折射率和粗糙度与波长相关的模型，进而建立偏振光谱模型。结果表面，此模型虽具有一定的误差，但总体有较高的准确度，能够反映物质的偏振光谱信息。

1 偏振双向反射分布函数的定义

偏振双向反射分布函数受到表面粗糙度、折射率、方位角等多个参数控制，将目标表面视为由一系列微小面元组成，并且小面元反射遵循菲涅耳反射[5]，通过描述物体表面的微观特征，能够较好的描述反射光的偏振状态。但模型中由于没有考虑反射光中的漫反射部分并且当物体表面粗糙度相对波长较小时存在衍射[3]，微面元模型不能很好的处理此类状况。

Kirchhof衍射理论分析了衍射的情况，采用Kirchhof理论进行BRDF建模[4，6]能够更好的反映物体表面的反射情况。Kirchhof理论对表面微观结果进行切平面近似，在切平面内认为是镜面反射。

粗糙物体表面的反射光通常包括镜面反射fsp、方向漫反射fdd和均匀漫反射fud三个部分

fBRDF=fsp+fdd+fud

(1)

双向反射分布函数的几何关系如图1所示，θi为入射角φi为入射方位角，θr为反射角，φr为反射方位角，Z是物体表面法线，ki和kr分别代表入射方向和观测方向的矢量，s和p分量则是垂直和平行入射面的或观测面的分量。

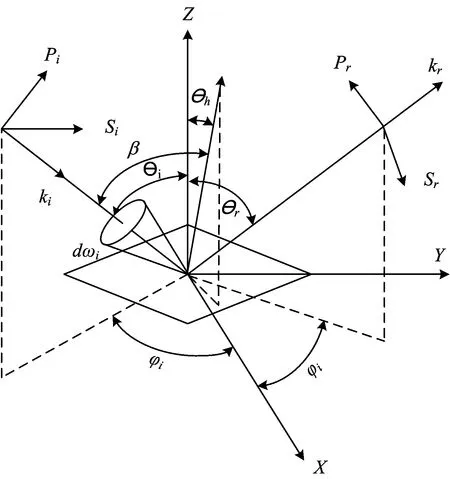
Fig.1 Coordinate system of bidirectional reflectance distribution

结合Kirchhof理论的切平面近似，可以得出镜面反射fsp为

(2)

其中，F为Fresnel反射系数，与表面材复折射率等因素有关，Δ是delta函数，反射光在反射圆锥内时为1，否则为0；g是表面粗糙度函数，与表面粗糙度δ相关。

方向漫反射fdd为

(3)

其中D是表面分布函数，与表面粗糙度δ相关。

均匀漫反射fud类似朗伯体反射为非偏振态，但会对增加总反射强度。其公式为

(4)

其中kud(λ)为目标表面多次散射形成的方向半球反射。

(5)

式中下标S表示电场分量垂直于入射面(入射方向和法线构成的平面)或探测面(探测方向和法线构成的平面)；下标p表示电场分量平行于入射面或探测面；上标r表示散射分量；上标i表示入射分量。针对上述微面元模型，引入四个参考平面，这四个参考平面分别为：入射方向分别与粗糙表面法线和微面元法线组成的平面，两面的夹角用ηi表示；散射方向分别与粗糙表面法线和微面元法线组成的平面，两面的夹角用ηr表示。那么，入射光和散射光可以表示为

(6)

其中

cosηi=[(cosθi+cosθr)/(2cosθh)-

cosθicosθh]/(sinθisinθh)

(7)

cosηr=[(cosθi+cosθr)/(2cosθh)-

cosθrcosθh]/(sinθrsinθh)

(8)

(9)

(10)

式中A和B的定义为

(11)

(12)

C=4n2k2+D

(13)

D=n2-k2-sin2β

(14)

其中n为折射率，k为吸收系数，N=n+ki为材质的复折射率。然而折射率并不是一个固定的值，在不同的波长下其值也会有所不同，折射率是一个与波长相关的函数[7]

(15)

其中A，B，C，D，E，F是待定常数，不同的物质有不同的值。而对于材质其吸收系数k也是随着波长的改变而发生变化，其计算方式如下[8]

(16)

其中λ为光的波长，K为物体的消光系数，ρ为物体的密度。结合上述可知，由于折射率n与吸收系数k皆与波长相关，所以复折射率N实际为一个随波长λ变化的函数即N(λ)。

根据式(7)—式(10)得到入射光和散射光之间的琼斯矩阵，实际应用中，Jonse矩阵和Mueller矩阵之间存在转换关系。为了能够更好的描述光的偏振态，而采用Stokes矢量和Mueller矩阵进行表示[9]。由于复折射率N与波长相关，所以对于Mueller矩阵中的各项元素也是随着波长的改变该变化，所以Mueller矩阵可表示为M(λ)。

除了折射率这一参数外，在模型中表面粗糙度函数g、遮蔽方程S、表面分布方程D均包含了另一个与波长相关的参数粗糙度δ2[10]。物体表面粗糙度δ的值，通常是利用特定波长下的入射光照射物体表面，并通过测量其反射光强度得到。其计算方式如下[11，12]

(17)

其中R为实测反射量，R0为理想平面下同等材质的反射。可以看出，粗糙度的测量与波长直接相关，在不同波长的探测光线下往往具有不同的测量结果。由于理想平面条件下物体表面绝对光滑，可以认为不产生漫反射，因此在不考虑吸收造成的损失时，R0可以用入射能量Ri进行代替。此时δ为

(18)

菲涅耳方程表示物体表面的反射率，即反射光与入射光的比值。此时将式中R/Ri部分用菲涅耳方程F(λ)替换，则公式变为

(19)

由于菲涅耳方程受到入射角θi及折射率n的影响。在上面的讨论中，因此折射率n受到波长λ的影响，菲涅耳方程与波长相关。因此粗糙度δ也是一个与波长相关的方程。

综上所述，对于折射率n和粗糙度δ两个关键参数都是受到波长影响，所以对于BRDF中的各个分量就可以完成基于光谱的建模。将标量BRDF中的镜面反射和方向漫反射部分转换为偏振表达式

(20)

(21)

fpj, k(λ)=fspj, k(λ)+fddj, k(λ)

(22)

式中j，k的取值范围是0～3，fpj, k为偏振镜面反射和偏振方向反射之和。均衡漫反射虽不具有偏振态，但增加总反射强度。此时可以将pBRDF表示为

(23)

式中L0，L1，L2和L3分别为反射光辐射亮度的Stokes参量，E0，E1，E2和E3为相应的入射光Stokes参量。

因为自然光为无偏振态，所以其矢量表示形式为

(24)

则反射光的偏振矢量为

(25)

由此可以计算偏振度为

(26)

由于在自然光条件下，反射光中圆偏振光成分很少，可以忽略不计，所以

(27)

2 仿真计算与分析

为了验证偏振光谱BRDF模型的正确性，分别在模拟折射率N随波长变化、粗糙度为固定值和折射率、粗糙度均随波长变化的情况下，与采用粗糙度、折射率均为常量的模型进行对比。在考虑粗糙度为常量的情况下，选择了δ=0.65μm，δ=0.45 μm，δ=0.25 μm三种粗糙度下的铝和δ=0.8 μm，δ=0.5 μm，δ=0.3 μm三种粗糙度下的塑料，并选择波长在650 nm下两种材质的折射率作为原模型参数进行模拟。同时为了验证仿真结果的正确性，将结果与参考文献[7，13]中的结果进行对比。

Fig.2 The simulation of aluminum of three conditions

(a): roughness and the refraction index both are constant; (b): the refractive index varies with wavelength, roughness is constant; (c): roughness and the refraction index vary with wavelength

Fig.3 The simulation of plastic of three conditions

(a): roughness and the refraction index both are constant; (b): the refractive index varies with wavelength, roughness is constant; (c): roughness and the refraction index vary with wavelength

图2为偏振光谱BRDF模型模拟铝材质在三种条件下的偏振特性。从图中结果可以看出，在三种情况下，铝的偏振度均会随着波长的增长而下降并在降低至一个极小值后，随着波长的增加而缓慢上升。并且，当粗糙度设定为常量时，在全波段范围内粗糙度越大，相应的偏振度越小，偏振度极小值所对应的波长也逐渐变小。

图3为偏振光谱BRDF对模拟塑料在三种条件下的偏振特性。从图中可以看出，在粗糙度为常量的情况下，整体偏振特性为先随波长下降，随后随着波长缓慢增长，并且在折射率为随波长变动的情况下，模拟结果显示其偏振度较折射率为常量的情况下略高。而当折射率和粗糙度均随波长变化时，偏振特性发生了一些变化，偏振度始终呈现下降趋势，初始时快速下降，后随波长增加而缓慢减少。

由上述结果可知，本工作提出的偏振光谱BRDF模型，在将粗糙度为常量、折射率采用随波长变化的情况和粗糙度、折射率随波长变化的两种情况下，均能够较为准确的描述物体表面的偏振特性。但通过与其他文献的测量数据进行对比时可以发现，仍旧存在着一些误差。对于误差产生的原因，可能包括两个方面：一是由于在对粗糙度进行光谱建模时将理想表面反射能量近似用入射光能量代替计算时产生；二是折射率反演过程中存在误差。

3 结 论

采用基于Kirchhof衍射理论的BRDF模型进行偏振光谱BRDF建模。建模过程中，主要针对模型中的两个主要参数折射率和粗糙度进行光谱建模。通过已有材质在不同波长下的折射率，对折射率进行反演，推导出折射率与波长的近似相关公式。在对粗糙度进行光谱建模时，参考经典的粗糙度测量方法，并结合菲涅耳反射定律推导出了粗糙度的光谱模型。在完成折射率和粗糙度的光谱建模后，将其带入标量BRDF方程并进一步转换pBRDF从而实现偏振光谱BRDF的建模。通过模拟结果与其他文献中的数据进行对比，本文的偏振光谱BRDF模型有较好的准确度，能够描述描述物体的偏振特性，但是本文模型的精确度依旧存在着一些误差。对于产生误差的原因可能是由于折射率和粗糙度的光谱建模过程中采用一些近似值所导致。后续工作主要集中在对折射率和粗糙度的波长模型加以调整，修正由使用近似值所产生的误差，能够较为准确的描述折射率和粗糙度与波长的关系，使偏振光谱BRDF模型能够更加准确的描述物体的偏振特性。

[1] Bartlett B D, Gartley M G, Messinger D W. Journal of Applied Remote Sensing, 2010, 4(1): 043552-21.

[2] Prokopenko V T, Alekseev S A, Matveev N V, et al. Optics and Spectroscopy, 2013, 114(6): 961.

[3] Priest R G, Gerner T A. Polarimetric BRDF in the Microfacet Model: Theory and Measurements, Naval Research Lab. Washington D C, 2000.

[4] He X D, Torrance K E, Sillion F X, et al. ACM SIGGRAPH Computer Graphics, 1991, 25(4): 175.

[5] Torrance K E, Sparrow E M. JOSA, 1967, 57(9): 1105.

[6] Li H, Torrance K E. Program of Computer Graphics, Tech. Rep. PCG-05-03, Cornell Univ., Ithaca, NY, 2005.

[7] Carlson E J. Development of a Spectropolarimetric Remote Sensing Caplbility, Air Force Inst of Tech Wright-Patterson AFB OH Graduate School of Engineering and Management, 2013.

[8] Volz F E. Applied Optics, 1972, 11(4): 755.

[9] FENG Wei-wei, WEI Qing-nong, WANG Shi-mei(冯巍巍，魏庆农，汪世美). Acta Optica Sinica(光学学报), 2008, 28(2): 290.

[10] GAO Ming, SONG Chong, GONG Lei(高 明，宋 冲，巩 蕾). Chinese Journal of Lasers(中国激光)，2013，(12): 225.

[11] Bennett H E J, Porteus J O. JOSA, 1961, 51(2): 123.

[12] Bennett H E. JOSA, 1963, 53(12): 1389.

[13] Goldstein D H. International Symposium on Optical Science and Technology. International Society for Optics and Photonics, 2000. 112.

Modeling and Simulation of Spectral Polarimetric BRDF

LING Jin-jiang, LI Gang, ZHANG Ren-bin, TANG Qian, YE Qiu

School of Computer and Information, Hefei University of Technology, Hefei 230009, China

Under the conditions of the polarized light, The reflective surface of the object is affected by many factors, refractive index, surface roughness, and so the angle of incidence. For the rough surface in the different wavelengths of light exhibit different reflection characteristics of polarization, a spectral polarimetric BRDF based on Kirchhof theory is proposee. The spectral model of complex refraction index is combined with refraction index and extinction coefficient spectral model which were got by using the known complex refraction index at different value. Then get the spectral model of surface roughness derived from the classical surface roughness measuring method combined with the Fresnel reflection function. Take the spectral model of refraction index and roughness into the BRDF model, then the spectral polarimetirc BRDF model is proposed. Compare the simulation results of the refractive index varies with wavelength, roughness is constant, the refraction index and roughness both vary with wavelength and origin model with other papers, it shows that, the spectral polarimetric BRDF model can show the polarization characteristics of the surface accurately, and can provide a reliable basis for the application of polarization remote sensing, and other aspects of the classification of substances.

Spectral polarimetric BRDF；Refraction index；Surface roughness

Aug. 1, 2014; accepted Dec. 18, 2014)

2014-08-01，

2014-12-18

国家自然科学基金项目(61271121)，中央高校基本科研业务费专项资金项目(J2014HGBZ0129)资助

凌晋江，1988年生，合肥工业大学计算机与信息学院硕士研究生 e-mail: lingjinjiang@hotmail.com

O433.1

A

10.3964/j.issn.1000-0593(2016)01-0042-05