利用FTIR和MODIS数据估算塔克拉玛干沙漠宽波段地表比辐射率

李火青， 吴新萍， 买买提艾力·买买提依明， 霍 文,杨兴华， 杨 帆, 何 清， 刘永强，4*

1. 新疆大学资源与环境科学学院， 新疆 乌鲁木齐 830046

2. 新疆且末县塔中气象站， 新疆 塔中 841000

3. 中国气象局乌鲁木齐沙漠气象研究所， 新疆 乌鲁木齐 830002

4. 绿洲生态教育部重点实验室， 新疆 乌鲁木齐 830046

利用FTIR和MODIS数据估算塔克拉玛干沙漠宽波段地表比辐射率

李火青1， 吴新萍2， 买买提艾力·买买提依明3， 霍 文3,杨兴华3， 杨 帆3, 何 清3， 刘永强1，4*

1. 新疆大学资源与环境科学学院， 新疆 乌鲁木齐 830046

2. 新疆且末县塔中气象站， 新疆 塔中 841000

3. 中国气象局乌鲁木齐沙漠气象研究所， 新疆 乌鲁木齐 830002

4. 绿洲生态教育部重点实验室， 新疆 乌鲁木齐 830046

分析并提供了一个利用MODIS窄波段数据， 估算地表宽波段(8～14 μm)比辐射率的最优估算方程， 并根据该方程获得了塔克拉玛干沙漠地区地表比辐射率特征分布情况。 首先， 沿塔克拉玛干沙漠的两条南北穿越公路， 使用傅里叶变换热红外光谱仪(FTIR)， 选取20个观测点， 获取实测的地表宽波段比辐射率。 其次， 利用MODIS温度产品MOD11A1和MOD11C1热红外区域第29， 31和32波段和MOD09A1近红外区域第7波段数据， 建立待定系数的地表宽波段比辐射率多元线性回归估算方程。 通过FTIR的观测值和MODIS数据确定该估算方程的系数， 并进行误差分析。 研究发现， 使用FTIR观测值， 由MODIS第29， 31和32波段数据的线性回归方程， 可以产生高精度的地表宽波段比辐射率。 加入MODIS第7波段后， 新的线性回归估算方程的精度更高， 均方根误差RMSE为0.004 5， 平均偏差Bias为0.000 1。 与文献中的其他六种估算方程横向对比， RMSE和Bias分别比其他六种估算方程低1和2个数量级。 最后， 利用该估算方程获得了研究区的地表比辐射率分布图， 结果显示， 沙漠中心区域的值为0.880～0.910， 平均值为0.906； 有稀疏植被区域的值为0.910～0.940； 靠近沙漠边缘的绿洲的值为0.950～0.980。

地表比辐射率； 塔克拉玛干沙漠； MODIS； FTIR

引 言

地表比辐射率是估算地表长波静辐射的基本参数， 也是研究地表能量辐射平衡的关键参数， 广泛应用于地-气间的物质与能量交换的陆面模式、 数值预报、 全球气候变化研究中[1-3]。 获得宽波段比辐射率光谱数据， 是准确计算比辐射率值最直接和有效的手段。 地表宽波段比辐射率光谱可以使用傅里叶变换热红外光谱仪(Fourier transform infrared spectrometer， FTIR)精确的测量[4-7]。 刘永强等[8]和Liu[9]利用FTIR首次研究了塔克拉玛干沙漠腹地的地表比辐射率。 FTIR观测方法的缺陷是不能获取区域值， 而热红外遥感技术是快速获取区域地表比辐射率的一种有效方法[10]。 但是， 热红外遥感只能获得特定的窄波段比辐射率， 不能代表宽波段比辐射率。 因此， 在一些区域， 由于缺乏足够的观测数据获取地表比辐射率， 其陆面模式中使用常数代替真实的宽波段比辐射率， 因而降低了地表温度反演的精度[11-12]。 Van等指出， 地表比辐射率偏差0.009， 会使反演的地表温度产生2～3 K的误差[13]。

许多研究者利用热红外遥感的窄波段数据， 建立宽波段比辐射率的线性拟合方程， 估算地表比辐射率。 Ogawa等[14]把宽波段的波长窗口确定为8～13.5 μm， 利用moderate resolution imaging spectrometer(MODIS)和advanced spaceborne thermal emission and reflection radiometer(ASTER)的比辐射率光谱库数据建立了宽波段比辐射率方程。 其方程采用MODIS第7(2.105～2.155 μm)， 29(8.400～8.700 μm)， 31(10.780～11.280 μm)和32(11.770～12.270 μm)波段范围的光谱库数据， 以29， 31和32波段的最大最小值之差和7波段数据， 组成2个变量1个常量的线性回归方程， 并且估算了撒哈拉沙漠地区地表的宽波段比辐射率。 Jin等[11]提出了一种基于MODIS热红外波段数据估算全球地表比辐射率的参数改进方法， 给出了宽波段窗口为8～14 μm的估算方程。 该估算方程同样使用MODIS和ASTER光谱库数据， 采用MODIS第29， 31和32波段范围的光谱库数据， 组成了三个变量的线性回归方程， 并应用于陆面过程， 通过模拟地表通量的误差， 验证估算方程的精度。 Tang等[15]比较了3～14和3～∞ μm两个宽波段窗口比辐射率的差异， 利用MODIS热红外第29， 31， 32波段数据建立三个变量一个常量的线性组合方程， 同样采用MODIS比辐射率光谱库验证估算精度。 王新生等[16]仅利用MODIS的第31和32热红外波段， 建立2个变量1个常量的线性组合方程， 估算宽波段比辐射率， 并且计算了全国地表比辐射率的年际和季度变化特征， 但是对方程的可靠性没有进行验证。 Cheng等[17]针对地表长波净辐射， 提出了最佳的宽波段窗口为8～13.5 μm， 根据ASTER和MODIS的比辐射率光谱库， 再结合地物(土壤、 岩石、 植被、 水、 冰/雪)样本的观测光谱数据， 使用MODIS第29和31波段， 获得了2个变量1个常量的宽波段比辐射率估算方程。 上述文献给出的宽波段比辐射率估算方程， 都是利用MODIS热红外第29， 31和32波段范围的光谱库数据建立方程， 在波段数和常数项的选择上也不相同， Ogawa等[14]还用到了第7波段的数据。 但是， 由于缺少地面现场的观测数据的验证， 仅使用光谱库数据进行验证， 导致这些估算方程在局部区域的适用性有限。

此外， Weng等[18]研究了一个新模型， 利用微波估算地物(雪， 沙漠， 植被)的比辐射率， 由于微波数据获取的局限性， 不适宜估算较大区域的宽波段比辐射率。 Sobrino等[19]利用NOAA(national oceanic and atmospheric administration)气象卫星影像数据， 通过NDVI(normalized difference vegetation index), TISI(temperature-independent spectral indices)和TS-RAM(thermal infrared radiance ratio model)三种方法反演地表比辐射率， 由于NOAA气象卫星的影像分辨率较低， 反演的比辐射率结果精度低。

针对上述估算地表宽波段比辐射率方法的不足， 结合本研究区域——塔克拉玛干沙漠的独特性和FTIR实测数据， 实施估算方程的完善和改进， 并分析研究区的地表比辐射率分布特征： (1) 估算方程同样采用线性组合方法拟合地表宽波段比辐射率， 方程不仅利用MODIS热红外波段数据， 还增加近红外波段数据； (2) 直接使用不同时期的FTIR实测宽波段比辐射率建立与验证估算方程， 而不是使用MODIS和ASTER的比辐射率光谱库数据； (3) 横向对比其他研究者利用MODIS数据得到的估算方程， 分析这些方程在塔克拉玛干沙漠区域的估算精度； (4) 根据最佳的估算方程， 估算并分析研究区的地表宽波段比辐射率的分布特征。

1 研究区和数据

塔克拉玛干沙漠位于塔里木盆地， 是世界第二大流动沙漠， 南北方向最宽520 km， 东西方向从西部弧顶喀什到弧边罗布泊长达1 300 km， 面积337 600 km2， 海拔高度800～1 300 m， 地势西高东低。 沙漠周边被不连续的大小绿洲包围， 沙漠内部沙丘连绵起伏， 一般高70～80 m， 最高可达250 m， 多为流动沙丘(图1)。 沙漠土壤类型单一， 以粉沙为主， 其中极细沙最多， 占到输沙量43.8%～75.5%， 主要成分都是石英， 还有少量的长石和白云母[20]。 位于沙漠腹地的塔中站(39°00′ N， 83°40′ E， 1 099.3 m)的1996—2013年观测数据表明， 沙漠腹地的年平均温度为12.4 ℃， 年平均降水仅23.0 mm， 而年平均潜在蒸发量高达3 800.0 mm。 有记录以来的最高温度为45.6 ℃， 最低温度为-32.7 ℃。 年平均风速为2.5 m·s-1， 瞬时最大风速为24.0 m·s-1[9]。

图1 沿两条沙面公路设置的FTIR观测点(图片来自Google Earth)

地表比辐射率与下垫面的土壤成分、 类型、 湿度和地表植被相关， 而研究区除周边的过渡带和绿洲之外， 其他区域无植被覆盖， 而且其土壤成份、 类型和湿度常年稳定不变。 在极端干旱的塔克拉玛干沙漠， 地表比辐射率值常年稳定。

1.1 FTIR观测数据

采用便携式傅里叶变换热红外光谱分析仪(FTIR)， 对塔克拉玛干沙漠地表宽波段比辐射率进行现场观测。 沿着两条沙漠公路(轮台至民丰沙漠公路， 阿拉尔至和田沙漠公路)选点， 观测点南北贯穿沙漠。 由于沙漠地表类型单一， 土壤成份及湿度变化极其微小， 每50～100 km选择一个合适的观测点， 在沙漠边缘靠近绿洲过渡带， 加密观测点。 为了提高观测结果的准确性， 选择在晴朗天气下测量[5]。 轮台至民丰沙漠公路的观测时间为2013年10月16日—19日， 阿拉尔至和田沙漠公路的观测时间为2014年9月27日， 共采集到20个观测点的地表宽波段比辐射率光谱数据(图1)。

1.2 MODIS数据

MODIS数据具有较高的光谱和时间分辨率， 每1～2 d可以获得一次全球观测数据， 对于监测大范围地表参数变化具有明显优势[21]。 MODIS有36个通道， 其中通道1～19和26分布在可见光和近红外波段， 其他16个通道分布在3～15 μm的热红外波段。 获取地表比辐射率最合适的热红外波段的大气窗口为8～14 μm， 相对应的波段为第29～32， 由于第30波段有较强的臭氧吸收， 无法利用。 因此， 热红外波段选择第29(8.400～8.700 μm)， 31(10.780～11.280 μm)和32波段(11.770～12.270 μm)。 此外， 处于近红外区域的第7波段(2.105～2.155 μm)数据是地表和云的反射率， 能够反映出地表土壤的属性， 姚云军等[22]指出， 第7波段对地表土壤的含水量敏感， 而地表比辐射率除了与地表土壤的类型、 结构、 有机质含量和表面特性有关之外， 土壤含水量是最重要的因素之一； Zhou等[23]也认为， 第7波段的反射率与土壤和岩石的宽波段比辐射率相关性最高； 本研究区富含石英(SiO2)沙， 有较高的地表反射率。 因此， 研究中增加了第7波段的数据。

MODIS第29， 31和32波段数据的分辨率均为1 km， 第7波段数据分辨率为500 m。 所有影像数据对应地表面积约1 300 km×500 km， 覆盖整个塔克拉玛干沙漠区域。 数据采集时间为2013年10月16日—18日。 MODIS数据可以从美国NASA(National Aeronautics and Space Administration)网站(http://modis.gsfc.nasa.gov)免费获取。

2 方 法

2.1 地表宽波段比辐射率的观测与计算

利用便携式傅里叶变换热红外光谱仪(Model 102F, Designs and Prototypes Ltd.)， 观测地表比辐射率光谱数据。 Model 102F快速傅里叶变换红外光谱分析仪(FTIR)的光通量为0.016 cm2·sr， 杂散辐射少， 其工作光谱范围为2～16 μm， 光谱分辨率为2～24 cm-1。 其测量结果可以达到标准差小于1%[6]。 地表比辐射率光谱的计算见式(1)

(1)

式(1)中，ελ是波长为λ时的地表比辐射率的光谱，Lλ(cm2·sr)是波长为λ时的地表辐射量度，Bλ(T)(cm2·sr)是波长为λ， 地表温度为T(K)时的黑体辐射量度， 下行辐射Dλ(cm2·sr)采用标定的漫反射金板进行测量。 Liu等[9]和刘永强等[8]给出了塔克拉玛干沙漠地表比辐射率光谱观测的操作过程和观测结果。

在陆面模式和数值预报模型中， 地表比辐射率一般使用宽波段比辐射率光谱的平均值。 波长范围在λ1～λ2之间的地表比辐射率的计算方法[24]

(2)

式(2)中，λ1和λ2是波长范围的上下限。 不同于Ogawa等[14[9]， 因此采用波长8～14 μm计算宽波段比辐射率。 由于ελ和Bλ(T)是连续函数， 为便于计算， 将积分方程离散化， 见式(3)

(3)

2.2 MODIS数据估计宽波段的比辐射率

MODIS热红外单波段的地表比辐射率值算法[25]为

(4)

式(4)中，fi(λ)是第i波段的光谱响应函数。 根据式(2)和式(4)， 宽波段比辐射率可以通过不同单波段的比辐射率线性组合[15]表示

(5)

式(5)中，

(6)

(7)

显然，gi是组合系数， 与温度为T时的黑体热辐射亮度有关， 与单波段的比辐射率无关。 基于此， 利用MODIS的第29， 31和32波段的数据， 通过多元线性回归方程的拟合， 可以得到宽波段比辐射率的估算方程。 由于MODIS第7波段与比辐射率高度相关， 增加第7波段数据到线性组合方程中， 并且分析增加第7波段前后对估算方程精度的影响。 定义宽波段地表比辐射率ε8～14方程为

(8)

或

(9)

其中，a1，a2，a3，a4，c为多元线性回归方程的系数，ε29，ε31和ε32分别为MODIS第29， 31和32波段的比辐射率值，α7是MODIS第7波段的反射率值。

3 结果与讨论

3.1 估算方程

根据20个观测点的FTIR观测值和同地点的MODIS影像值， 利用多元线性回归方法， 拟合出式(8)和式(9)的系数， 建立对应的地表宽波段比辐射率估算方程分别为

(10)

和

(11)

分析式(10)和式(11)的估算值与观测值的均方根误差(RMSE)， 分别为0.005 1和0.004 5， 估算方程在增加了第7波段的地表反射率后， RMSE减少了11.8%。 表1给出了式(11)的估算值和未参与建模的另外16个观测值对比， 只有观测点8的偏差(Bias)较大， 达到0.011， 其他观测点的|Bias|≤0.007。 图2给出了估算值对观测值的拟合度， 显然， 式(11)对塔克拉玛干沙漠地表宽波段比辐射率的估算不仅有效， 而且精度高。

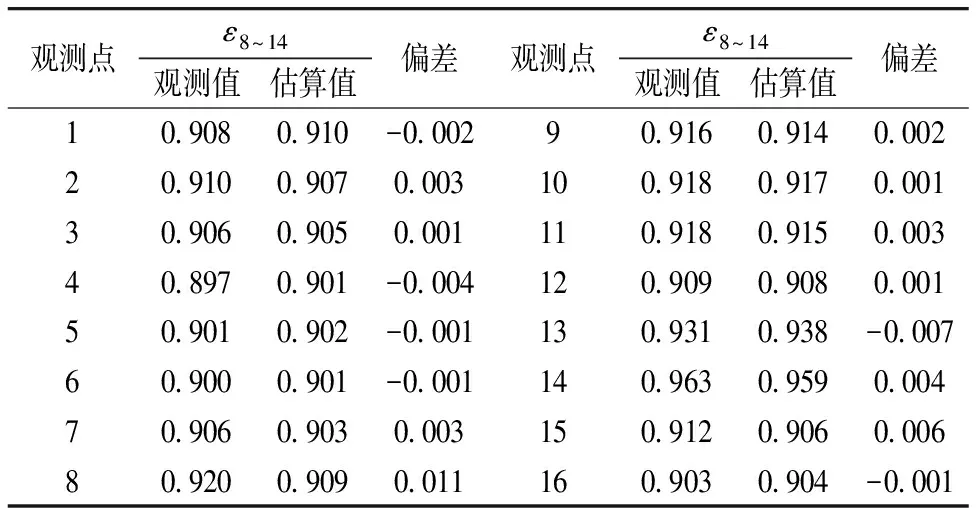
表1 FTIR观测值与方程估算值的对比

3.2 估算方程对比

选择文献提供的六种光谱波长范围在8～14 μm内的不同估算方程， 与式(11)进行横向对比。 对比六种估算方程给出的MODIS估算值与FTIR观测值的RMSE和Bias(表2)， 可见六种方程的RMSE和Bias比式(11)分别大1和2个数量级， 并且均为负值， 即估算值与实测值相比偏大。 所以， 式(11)对塔克拉玛干沙漠的地表比辐射率估算最优。

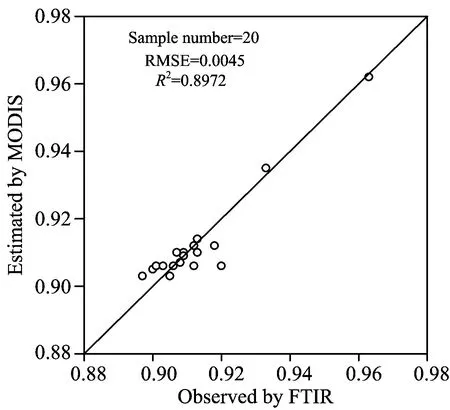
图2 地表宽波段比辐射率的FTIR观测值与

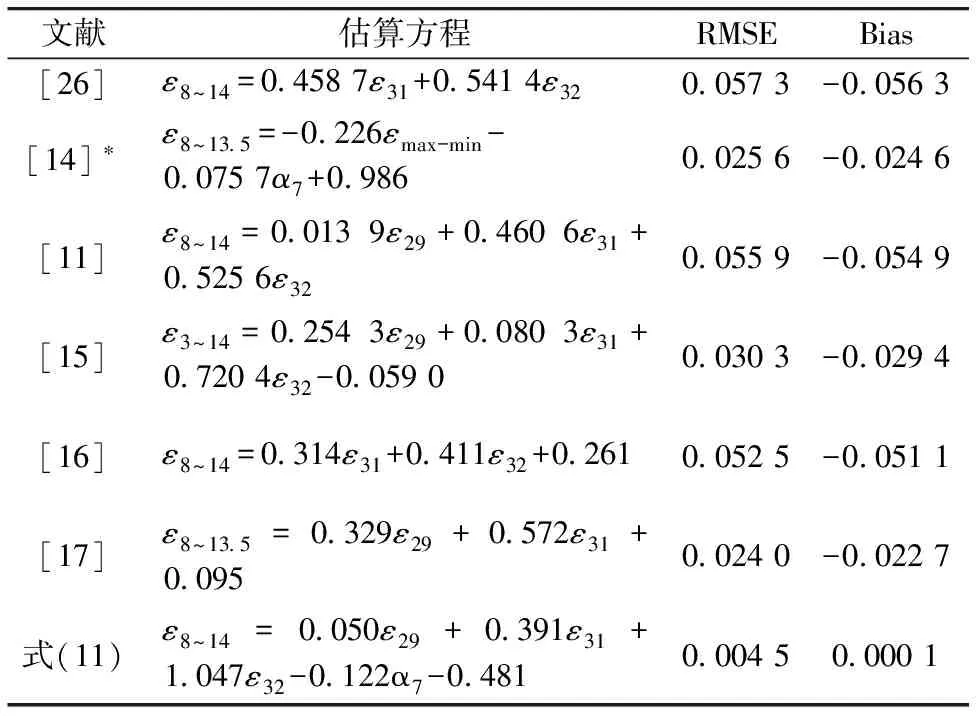
文献估算方程RMSEBias[26]ε8～14=0 4587ε31+0 5414ε320 0573-0 0563[14]∗ε8～13 5=-0 226εmax-min-0 0757α7+0 9860 0256-0 0246[11]ε8～14=0 0139ε29+0 4606ε31+0 5256ε320 0559-0 0549[15]ε3～14=0 2543ε29+0 0803ε31+0 7204ε32-0 05900 0303-0 0294[16]ε8～14=0 314ε31+0 411ε32+0 2610 0525-0 0511[17]ε8～13 5=0 329ε29+0 572ε31+0 0950 0240-0 0227式(11)ε8～14=0 050ε29+0 391ε31+1 047ε32-0 122α7-0 4810 00450 0001

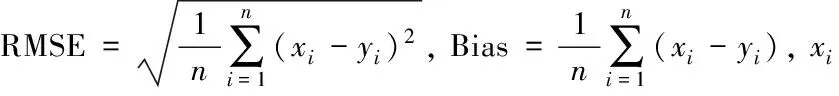
3.3 塔克拉玛干沙漠地表比辐射率分布特征

选取2013年10月20日的塔克拉玛干沙漠区域MODIS数据， 利用式(11)和第7， 29， 31和32波段数据， 估算研究区的地表宽波段比辐射率。 区域范围为1 300km×500km， 包括整个塔克拉玛干沙漠以及塔里木盆地周边绿洲和天山南部及昆仑山北部分山区(图3)。 可以看出， 塔克拉玛干沙漠区域的地表比辐射率集中在0.880～0.910之间， 面积分布最大， 变化幅度较小。 沙漠中有稀疏植被区域的范围在0.910～0.940之间， 靠近沙漠边缘绿洲(轮台、 阿拉尔、 且末、 喀什地区绿洲)的范围在0.950～0.980之间。

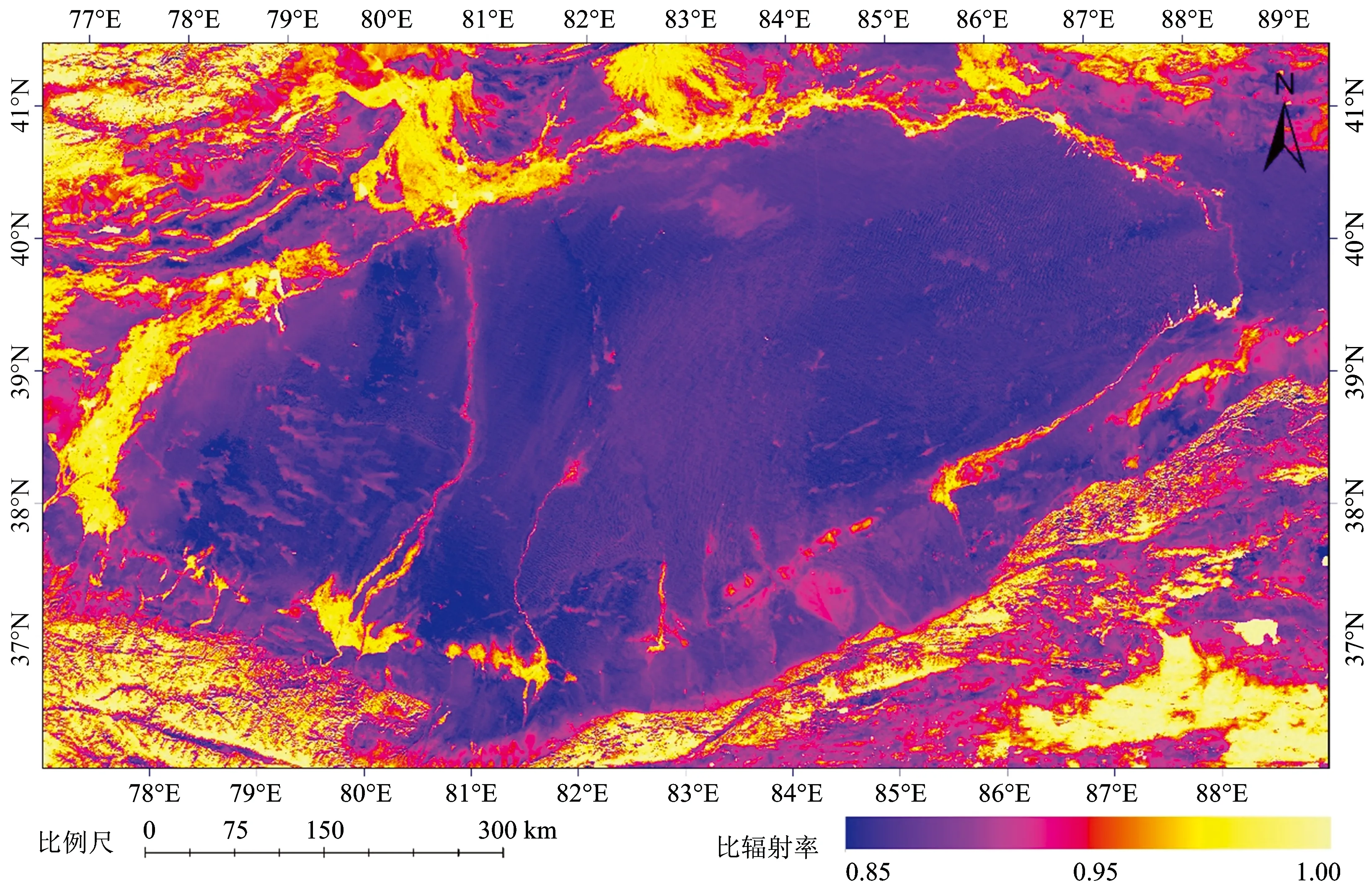
图3 塔克拉玛干沙漠地区地表比辐射率分布特征

4 结 论

地表宽波段比辐射率是研究地表能量平衡的重要参数。 使用傅里叶变换热红外光谱仪， 南北穿越两条沙漠公路， 获得20个观测点的地表宽波段比辐射率光谱数据， 计算出每个观测点的地表比辐射率值。 结合同期的MODIS第29， 31和32波段1 km分辨率的地表比辐射率， 和第7波段500 m分辨率的地表反射率， 建立估算地表宽波段比辐射率多元线性回归方程。

方程估算值与观测值的误差对比发现， 加入第7波段后的估算方程精度更高， 均方根误差RMSE为0.004 5。 进一步与其他六种估算方程横向对比， RMSE和Bias分别比其他六种估算方程低1和2个数量级。 采用本估算方程计算了塔克拉玛干沙漠区域的宽波段比辐射率分布特征， 沙漠中心区域的值为0.880～0.910， 平均值为0.906。 沙漠中有稀疏植被区域的值为0.910～0.940， 靠近沙漠边缘绿洲的值为0.950～0.980。

估算方程的特别之处在于： 利用地表比辐射率的实测数据， 而不是光谱库数据， 建立和验证估算方程， 不仅方程的精度高， 而且避免缺乏实证检验而导致的误差； 增加近红外波段再次提高方程的精度。 该估算方程对极度干旱的塔克拉玛干沙漠区域有较高的适用性， 为下一步进行该区域的陆面和数值预报模式的模拟提供了支持。 该估算方程对其他植被覆盖区和湿润地区的适用性有待于进一步的研究。

[1] Sellers P J, Randall D A, Collatz G J, et al. Journal of Climate, 1996, 9(4): 676.

[2] Jiang G M, Li Z L. Remote Sensing of Environment, 2006, 105: 326.

[3] Liang S, Wang K, Zhang X, et al. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2010, 3(3): 225.

[4] Hook S J, and Kahle A B. Remote Sensing of Environment, 1996, 56(3): 172.

[5] Korb A R, Dybwad P, Wadsworth W, et al. Applied Optics, 1996, 35(10): 1679.

[6] Korb A R, Salisbury J W, D’Aria D M, et al. Journal of Geophysical Research: Solid Earth, 1999, 104(B7): 15339.

[7] Hori M, Aoki T, Tanikawa T, et al. Remote Sensing of Environment, 2006, 100(4): 486.

[8] LIU Yong-qiang， Ali Mamitimin， HUO Wen, et al(刘永强, 艾力·买买提明, 霍 文, 等). Desert and Oasis Meteorology(沙漠与绿洲气象), 2014, 8(3): 1.

[9] Liu Y, Mamtimin A, Huo W, et al. Journal of Mountain Science, 2014, 11(6): 1543.

[10] Sobrino J A, Raissouni N, Li Z L. Remote Sensing of Environment, 2001, 75(2): 256.

[11] Jin M, Liang S. Journal of Climate, 2006, 19(12): 2867.

[12] Hulley C C, Hook S J, Baldridge A M. Remote Sensing of Environment, 2010, 114: 1480.

[13] Van de Griend A A, Owe M. International Journal of Remote Sensing, 1993, 14(6): 1119.

[14] Ogawa K, Schmugge T. Earth Interactions, 2004, 8(7): 1.

[15] Tang B H, Wu H, Li C, et al. Optics Express, 2011, 19(1): 185.

[16] WANG Xin-sheng, XU Jing, LIU Fei, et al(王新生, 徐 静, 柳 菲, 等). Acta Geographica Sinica(地理学报), 2012, 67(1): 93.

[17] Cheng J, Liang S, Yao Y, et al. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 401.

[18] Weng F, Yan B, Grody N C. Journal of Geophysical Research: Atmospheres (1984—2012), 2001, 106(D17): 20115.

[19] Sobrino J A, Jiménez-Muoz J C, Sòria G, et al. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(2): 316.

[20] WANG Xun-ming, DONG Zhi-bao, CHEN Guang-ting(王训明, 董治宝, 陈广庭). Journal of Desert Research(中国沙漠), 2001, 21(1): 56.

[21] Wan Z. Remote Sensing of Environment, 2014, 140(1): 36.

[22] YAO Yun-jun, QIN Qi-ming, ZHAO Shao-hua, et al(姚云军， 秦其明， 赵少华， 等). Journal of Infrared and Millimeter Waves(红外与毫米波学报), 2011, 30(1): 9.

[23] Zhou L, Dickinson R E, Ogawa K, et al. Geophysical Research Letters, 2013, 30(20): 2026.

[24] Wilber A C, Kratz D P, Gupta S K. Surface Emissivity Maps for Use in Sutellite Retrievlas of Longwave Radiation. NASA Tech. Publication NASA, 1999. 209362.

[25] Wan Z, Dozier J. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(4): 892.

[26] Wan Z, Li Z. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(4): 980.

Estimating Surface Broadband Emissivity of the Taklimakan Desert with

FTIR and MODIS Data

LI Huo-qing1, WU Xin-ping2, Ali Mamtimin3, HUO Wen3, YANG Xing-hua3, YANG Fan3, HE Qing3,LIU Yong-qiang1,4*

1. College of Resources and Environmental Sciences, Xinjiang University, Urumqi 830046, China

2. Tazhong Weather Station of Qiemo in Xinjiang, Tazhong 841000, China

3. Institute of Desert Meteorology, China Meteorological Administration, Urumqi 830002, China

4. Key Laboratory of Oasis Ecology (Ministry of Education), Urumqi 830046, China

Surface broadband emissivity in the thermal infrared region is an important parameteras for the studies of the surface energy balance. This paper analyzed and offered an equation to estimate the surface broadband emissivity for the spectral domains 8～14 μm against the MODIS data, and then, the distribution characteristic of surface emissivity for Taklimakan Desert was obtained with this equation. Firstly, along two highways crossing the Taklimakan Desert, twenty sample sites were selected and their spectral of broadband emissivity were observed with Fourier Transform Infrared spectrometer (FTIR). Secondly, using the Moderate Resolution Imaging Spectrometer (MODIS) land surface temperature and emissivity product MOD11A1 and MOD11C1, derived emissivities in three thermal infrared channels 29 (8.4～8.7 μm), 31 (10.78～11.28 μm) and 32 (11.77～12.27 μm) and MODIS surface reflectance products MOD09A1, derived reflectance in near-infrared channel 7 (2.105～2.155 μm), developing an empirical regression equation to convert these spectral emissivities and reflectance to a broadband emissivity. The FTIR data were used to determine the coefficients of the regression equation, another part of FTIR data were used to investigate the accuracy of equation. It was found that the equation consist of MODIS channels 29, 31 and 32 has more accuracy; furthermore, the accuracy is improved when channel 7 data was added in the regression equation. The root mean square error (RMSE) and Bias were 0.004 5 and 0.000 1, respectively. Comparing to other six equations originated from literatures, which also estimate the surface broadband emissivity from narrowband emissivities. The RMSE and Bias of our equation are lower one order and two orders of magnitude than other six equations, respectively. Lastly, our equation is applied in the Taklimakan Desert area to build a distribution image of emissivity based on MODIS data. It demonstrates that the emissivity of Taklimakan Desert is in the range of 0.880～0.910 over the central regions, the averaged value is 0.906; The emissivity is in the range of 0.910～0.940 where the areas covered by spare vegetation; The emissivity is in range of 0.950～0.980 where the regions near to the oasis.

Emissivity; Taklimakan Desert; MODIS; FTIR

Sep. 26, 2015; accepted Dec. 18, 2015)

2015-09-26，

2015-12-18

国家自然科学基金项目(41265002， 41175140)， 公益性行业(气象)科研专项(GYHY201306066)资助

李火青， 1990年生， 新疆大学资源与环境科学学院硕士研究生 e-mail: 1092694095@qq.com *通讯联系人 e-mail: lyqxju@163.com

TP722.6

A

10.3964/j.issn.1000-0593(2016)08-2414-06

*Corresponding author