基于红黑树数据结构的海岸线无人机正射影像拼接研究

范诗玥，张峰，卢文虎，王晶，王丰，刘庆群（国家海洋信息中心，天津　300171）



基于红黑树数据结构的海岸线无人机正射影像拼接研究

范诗玥，张峰，卢文虎，王晶，王丰，刘庆群
（国家海洋信息中心，天津300171）

摘要：随着无人机技术的快速发展，以测量为目的的无人机摄影测量技术已广泛应用到各行各业。相比于常用测量技术，无人机摄影测量技术需要处理抖动平台下的序列摄影图像，技术难度更大。利用红黑树数据结构实现无人机摄影图像的大尺度特征点匹配连接，基于相机标定和捆绑调整两个无人机摄影测量的关键技术环节，实现无人机海岸线遥感影像的快速拼接。

关键词：无人机摄影测量；大视角图像匹配；红黑树数据结构；影像正射拼接

经过近60年发展，摄影测量理论及技术已日趋成熟，并广泛应用于城市建模、国家三四等水准测量等行业（王之卓等，1979；李德仁等，1992；Edward et al，2001；张剑清等，2003）。摄影测量主要是把专业测量相机安装在稳定有人机平台上，在飞行前进行严格航迹规划及精确地控制相机曝光间隔，利用高质量飞行影像解算相机外方位元素和地面三维点，并在此基础上通过密集匹配、镶嵌线提取等操作实现DEM（数字高程模型）、DSM（数字表面模型）及DLG（数字线化模型）等数字化产品生产。然而，这种常规摄影测量技术并不适用于所有场景，比如地震灾区、偏远海岸线等人无法到达的复杂、敏感环境。随着飞控、导航等技术发展，无人机技术近十年得到飞速发展（唐强等，2004；聂博文等，2007），民用无人机技术现已应用到地质勘查、遥感等领域（孙杰等，2003；李宗南等，2014）。由于无人机载荷有限以及无人机飞行失败风险性系数偏大，搭载在无人机平台上的相机较有人机在飞行中易受到风、气流影响，所拍摄相片在尺度、亮度、角度上存在较大变化，故给无人机影像特征提取匹配增加难度。以上这些因素都将严重影响到测量定位及数字化产品的精度。

具有空间信息的拼接技术已广泛应用于航天、航空及无人机领域，具有代表性的工作如下。为解决卫星拼接像元失配的问题，常琳等（2014）提出了一种实现TDI CCD相机像元快速拼接配准的匹配算法。张过等（2012）以基于多CCD影像重成像算法作为内视场拼接的技术手段，实现航空飞机雷达地形测绘DEM的影像拼接。刘春等（2012）以稀少控制信息的无人机影像严格拼接为目的，引入光束法自由网平差技术实现无人机影像拼接。

无人机影像特征提取匹配和同名点转点算法是实现遥感影像拼接的基础，在国内外有大量研究人员进行相关研究，基本思路大致相同，即直接通过中间影像上的特征点坐标进行直接比较和串点（Barazzetti，2010）。此类方法在处理小分辨率影像时，效率可以接受，但是对于大尺度无人机遥感影像时，候选特征点过多造成了效率极其低下。所以，本文利用红黑树数据结构实现无人机摄影图像的大尺度特征点匹配连接，同时根据无人机相机标定和捆绑调整等关键技术环节，将无人机摄影技术应用到海岸线数字化生产中，制作正射拼接影像产品。

1　无人机相机标定

1.1畸变纠正几何模型

理想透视模型的物理原型为针孔成像模型，物和像会满足直线投影关系。但是无人机相机并不像常规航测用途的专业相机，相机光学系统存在加工和装配的误差，像点和对应地面点不满足严格的共线条件，因此在相机图像平面上实际所成的像与理想成像之间存在畸变，相机成像理想点和实际点存在差异。利用图像来进行测量，从而反算出相机的内外参数及其三维点坐标时，第一步应是相机标定，去除相机的畸变因素。

相机几何畸变包括径向畸变和切向畸变（张剑清等，2003），相比于切向畸变，径向畸变更大。像点（xr和yr）两个方向的径向畸变纠正模型和可以用下面的公式标定。

其中，k1、k2....为径向畸变系数，通常情况下，二阶模型可以满足实际的精度，所以本文选用二阶模型来刻画径向畸变函数，即公式（2）。

切向畸变纠正模型可以用公式（3）表示。

其中，p1、p2为切向畸变系数，实际使用中，删除高阶项o［（xryr）4］。

综合上述径向畸变模型（公式（2））和切向畸变模型（公式（3）），得到最后完整的相机畸变几何纠正模型，如公式（4）。

其中像点（ui和vi）是经过畸变几何纠正的坐标，从而消除了仪器制造工艺误差带来的非共线的实验条件。

1.2相机标定方法

本文利用像点作为真值，优化径向畸变参数（k1k2）和切向畸变参数（p1p2）。假设从图像上提取出一系列特征点（ui和vi），将上面4个参数当作待求参数，利用最小二乘非线性迭代优化中求出准确的值。非线性优化中，需要对上面4个参数分别求导，导数如公式（5）和（6）。

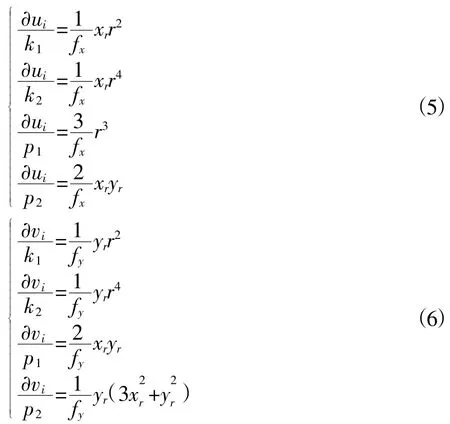
公式（5）和公式（6）组成偏导数矩阵，如：

给定畸变参数初值后和已知偏导数矩阵J，可以通过公式（8）计算得到畸变参数改正值。

其中，e为像点改正数。

当标定得到准确的径向和切向畸变参数后，通过公式（4）可以将原始无人机图像纠正为无畸变的无人机图像。

实际实现过程中，首先需要从图像中获取稳定高精度匹配特征点，这些特征点将作为优化问题的观测真值。然后根据公式（7）计算优化问题的一阶导数，通过公式（8）进行多次迭代。每次迭代优化后的变量增值将加入到初值中，作为下一次迭代初值，直至问题收敛。当问题收敛后，从变量中提取出相机畸变参数。

2　无人机大视角图像特征提取匹配

2.1立体像对同名点提取匹配

特征点提取在航空测量中至关重要，只有匹配后的同名点才能唯一确定三维点坐标，才能用于相机定姿和定位。本小节主要介绍如何从立体像对中获取高精度匹配的同名点。由于无人机拍摄的随意性，即两两图像间在尺度、亮度、几何变换中存在很大差异，故需要研制一种对尺度、亮度、旋转不变的特征点提取匹配算法。尺度不变特征提取算法（SIFT）是Lowe（1999）在1999年发表、2004年完善总结的一种计算机视觉算法，用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量。如图1所示，分别对左、右影像进行SIFT特征提取，最后利用尺度不变特征变换算法进行匹配。

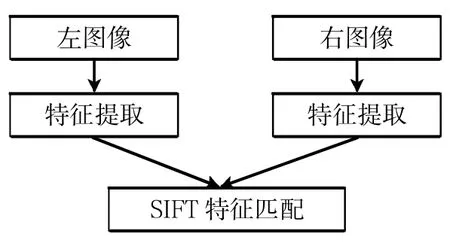
图1　SIFT算法框架图

不同于其他特征点提取匹配算法，SIFT算法因考虑到高斯尺度空间和高斯差分尺度空间，对尺度和噪声有很强抗敏感性。高斯尺度空间是将原始无人机图像通过不同高斯卷积核产生一阶图像，选取一阶图像中某一张进行图像降采样得到第二阶图像的第一张，然后利用高斯卷积核对此图像进行卷积运算得到二阶图像，以此得到连续的尺度空间。高斯差分金字塔通过高斯金字塔中相邻尺度空间函数相减即可，它最大的优点是计算简单，主要作用是减少噪声干扰。

SIFT算法流程分三大步：第一步是SIFT特征点的检测；第二步是SIFT特征描述符的生成；第三步是SIFT特征向量的匹配。其中第一步最为关键，其原理为寻找尺度空间极值点，每一个采样点都要和它同尺度的8个相邻点和上下相邻尺度对应的18个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点，得到某个尺度上的极值并保存它的尺度和位置信息。得到区域极值后，还需进一步精确定位特征点。首先可以根据具体情况将阈值设定为一个数值，尺度空间中灰度值若小于该值则抛弃。再通过拟和三维二次函数以精确确定关键点的位置和尺度（达到亚像素精度），同时去除低对比度的关键点和不稳定的边缘响应点（因为高斯差分算子会产生较强的边缘响应），以增强匹配稳定性、提高抗噪声能力。故SIFT提取特征点并不是几何特性的极值点，而是灰度空间的极值。

SIFT特征提取算法可以提供含有方向和梯度的128维描述符信息，所以实现两张影像特征点匹配可以根据128维描述符在空间中的最短欧式距离来判断。为了避免噪声的干扰，对于一张影像中待匹配的兴趣点，假如在另一张影像中的所有像点中，欧式距离的最短距离和次短距离小于给定的阈值，就认为这对特征点匹配。

2.2红黑树多图像连接点生成

在摄影测量航线规划中，对航向和旁向摄影重叠度均有严格要求，所以一个地面点会在多张影像上成像，所有这些像点组成的集合被定为连接点。相比于只有两次观测的立体像对同名点，三次及更多的连接点可以为捆绑调整优化特征点提供更丰富的多余信息，从而提高定位定向的精度。另外，连接点还可以实现两两像对的连接，实现整体模型的尺度归一化。因此，连接点生成在摄影测量中非常重要，为捆绑调整提供必要的输入信息量。

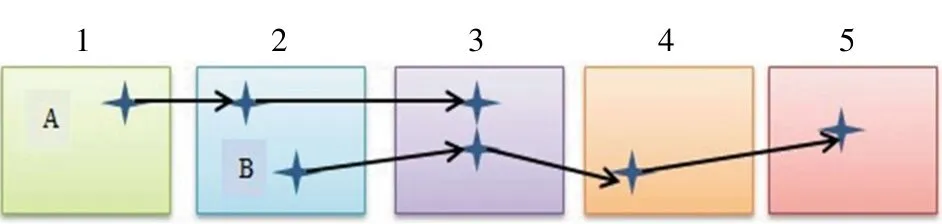
图2　连接点示例图

如图2所示，总共拍摄了5张序列影像，图像的编号分别为1、2、3、4、5。有两组连接点，分别为A（被第1、2、3张影像观测到，总观测次数为3）和B（被第2、3、4、5张影像观测，总观测次数为4）。由于使用特征点提取匹配只能得到两张影像的同名像点对，无法直接转点。例如使用特征提取匹配算法SIFT分别匹配第一、二张影像得到，第二、三张影像得到，然后需要判断，是否为同名像点。假如这两对特征点指示相同的地面点，需要将其合并得到A。将所有特征提取匹配算法得到的单对同名像点连接得到连接点转点。由于没有任何信息，实现和连接只能通过两对公有的图像信息，即第二张影像的图像坐标是否相同；倘若相同，认为其为相同的同名像点，从而实现转点。但使用SIFT算法可以从一对相邻图像对中得到上千甚至上万个同名像点对，因此在海量数据点对中去直接比较图像坐标来实现转点的效率将极为低下。红黑树是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。本文利用红黑树数据结构，设计了一种适用于建立特征点空间关系的数据结构，大大提高了连接点转点的效率。

对于特征点数据，可以利用红黑树数据结构加速连接点转点过程。相比于其它二叉树，除了拥有键值和键值对应数据外，还包含颜色属性。图3为一棵包含6个节点的红黑树，每个节点左边表示键值，右边表示键值对应的内容（i表示第i个连接点），键值颜色为红色或者黑色。每个连接点的键值索引可以设为如下数据结构形式：

struct RB_Key

｛

int imgNo；

float u；

float v；

｝；

其中，imgNo为图像序号，u、v为图像坐标。在进行连接点转点的过程中，只需要比较键值就可以快速进行特征点转点。

为了更清晰了解整个搜索过程，下面通过图2中的第一个特征点A来说明。A特征点被3张影像共同观测到，分别为图像1、2和3。利用2.1节提出的方法分别进行两次提取和匹配，得到两个特征点分别为和（每个括号表示一个像点，每像点包括图像序号和图像坐标）。在判断是否与属于同一个特征点时，将第二个像点作为键值，将第一个像点作为键值，只需要在图3中搜索键值。当找到相同键值时，连接两个像点，得到3次观测的特征连接点，

即

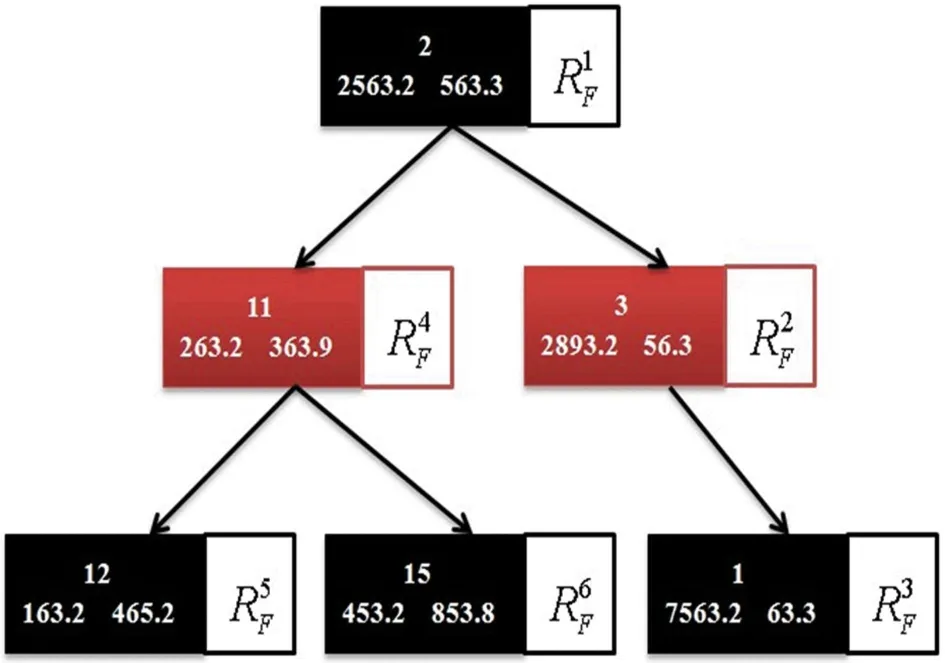
图3　红黑树数据结构示例图

3　捆绑调整

捆绑调整主要作用是利用第2节提供的匹配特征点作为观测，并利用像点和三维点的相机成像模型估计出拍摄状态下的相机位姿和三维点。首先介绍应用到捆绑调整模型的相机成像坐标系统转换关系，最后介绍捆绑调整的数学原理。

3.1坐标系变换关系

相片坐标系、像平面坐标系、摄影坐标系、大地坐标系是摄影测量最重要坐标系，四者间的相互转换关系如下。

（1）像平面坐标（x，y）与相片坐标（像素坐标）（u，v）

其中，（u0，v0）为相片内方位元素，r′为倾斜因子，dx和dy为CCD每个象元的实际尺度。

（2）摄影坐标（Xc，Yc，Zc）与像平面坐标（x，y）

（3）摄影坐标（Xc，Yc，Zc）与大地坐标（XW，YW，ZW）

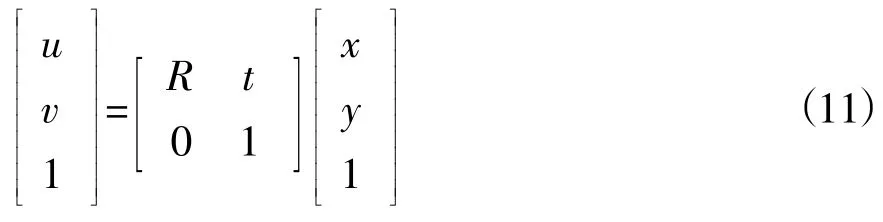
其中，R为旋转量，t为平移量。

（4）合并得到相片坐标（u，v）与大地坐标（XW，YW，ZW）

其中，fu=，fv=，r = r′f。K为相机内参数矩阵，P= K［ R t］相机投影矩阵，M为大地坐标。

最后得到图像坐标（u，v，1）和大地坐标（XW，YW，ZW）相互关系。图像坐标和三维大地坐标组成的小孔成像模型将作为捆绑调整的平差基本单元。

3.2捆绑调整的非线性优化

捆绑调整的数学本质为非线性最小二乘优化问题，即给定观测值来估计最优的优化参数。如式（12）中，观测值Z为第2节提取匹配到的连接点，优化参数X包括相机的外方位元素和连接点的三维坐标。摄影测量中，每个相机的外方位元素包括6个变量，分别为3个线元素和3个角元素；每个特征点包括3个变量。假设n张图像，观测到m个地面点，同时投影到所有图像形成k个投影点。此时，观测量Z个数为k×2 j，优化参数个数为n×6 + m×3。则捆绑调整算法的非线性最小二乘问题，就是要找到一个状态向量X，使得最小化。

其中，假设所有特征点所对应的投影像点坐标的不确定度是相同的，并且是互相独立的。因此在光束法平差算法中，将用Σ-1Z= I作为权重。

4　海岸线正射影像拼接

4.1整体实验方案设计

整体实验方案包括相机畸变校正、红黑树特征匹配、相机初始化、捆绑调整和正射拼接5个主要步骤（图4），详细过程如下：

图4　无人机测量实验方案设计

（1）相机畸变校正：由于无人机海岸线测量使用的是普通相机，镜头存在径向畸变和切向畸变，直接使用原始图像的信息，无法准确描述像点与其对应地面点的线性关系，因此需要利用径向畸变参数和切向畸变参数纠正所有拍摄的图像。

（2）红黑树特征匹配：原始图像信息无法直接应用于后续的信息处理，需要利用尺度不变特征变换算法得到大量高精度的稳定的特征点，然后利用RANSAC算法（Fischler et al，1981）去除用SIFT算法所得特征点中的错点；对连续多对图像两两进行特征提取，然后利用红黑树结构，快速对多张具有重叠图像的特征点进行连接，生成具有丰富信息的连接点信息。

（3）相机初始化。下一步的捆绑调整计算属于非线性问题中的最小二乘问题，需要为非线性优化问题提供较准确的初始值。

（4）捆绑调整。整合标定后的相机内参数、连接点数据和相机初始值，利用Levenberg-Marquardt算法（伏燕军等，2007）实现捆绑调整。捆绑调整可以得到两类优化数据结构，其一是参与优化的连接点对应的三维特征点的空间坐标，其二是安装在无人机上的相机6个位置姿态信息。

（5）正射拼接：利用捆绑调整后得到的三维特征点空间坐标和相机6个姿态参数进行拼接，得到正射拼接影像。正射拼接的目的是实现相机从透视成像向平行方式成像。根据捆绑调整得到的稀疏三维点，通过拟合加密得到地形场景。然后，实现每个点在相片上的单张微分纠正。纠正后的影像将带有具体的地理坐标信息，根据坐标的统一性，可直接实现影像拼接。

4.2海岸线无人机影像正射拼接

海岸线数字化产品中，正射拼接影像有着重要的作用与意义。本小节将4.1方案得到的相机外方位元素和三维点，利用间接法实现单张相片微分纠正。微分纠正后的每张相片都归一化到大地坐标系统，因此，直接通过坐标平移就可以实现整个海岸线测区的单张纠正后影像的拼接，最后得到一张完整覆盖该测区的正射拼接影像。

实验中利用无人机拍摄的6张海岸线影像（图5）进行基于红黑树数据结构特征匹配，匹配结果如图6和图7所示。图6是利用前两张图像提取得到10 342个匹配特征点（红色点表示），其中两张图像同名像点用绿色直线连接（图7）。最后，根据各影像匹配生成的同名像点及计算得到的相机参数进行反算，拼接成正射影像结果如图8所示。

图5　原始影像

图6　同名点匹配结果

图7　同名点连接结果

倘若需要对拼接结果进行定量分析，需要通过大量控制点作为检查点进行衡量。因为本文数据缺乏控制点，所以只能通过目视方式进行定性分析。实验表明，不同影像边缘上的道路线拼接后无缝隙，无明显像素偏移，证明了该方法的可行性。

图8　无人机海岸线影像拼接结果

5　总结

利用红黑树数据结构优化了无人机影像大视角的特征点匹配，实现了快速、精确的同名像点提取，通过捆绑调整得到的三维地形及相机优化参数反算，完成正射影像拼接生产，实验结果显示，该拼接方法对拼接后影像中海岸线的连续性无任何影响，效果良好。本方法为海岸线数字化及海岸线变迁分析工作提供了一种技术支撑手段。

参考文献

Barazzetti L，Remondino F，Scaioni M，2010. Extraction of accurate tie points for automated pose estimation of close-range blocks. In：ISPRS Technical Commission III Symposium on Photogrammetric Computer Vision and Image Analysis.

Edward M M，James S B，Chris J M，2001. Introduction to modern photogrammetry. Wiley press.

Fischler M，Bolles R，1981. Random sample consensus：a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM，24（6）: 381-39.

Lowe D G，1999. Object recognition from local scale-invariant features. In：IEEE international conference on computer vision（ICCV），2: 1150-1157.

常琳，金光，杨秀彬，2014.航天TDI CCD相机成像拼接快速配准算法设计与分析.光学学报，34（5）：48-56.

伏燕军，杨坤涛，邹文栋，等，2007.基于Levenberg-Marquardt算法的图像拼接.激光杂志，28（5）：46-48.

李德仁，郑肇葆，1992.摄影测量学.北京：测绘出版社.

李宗南，陈仲新，王利民，等，2014.基于小型无人机遥感的玉米倒伏面积提取.农业工程学报，30（19）：207-213.

刘春，李巍岳，雷伟刚，等，2012.基于光束法自由网平差的无人机影像严格拼接.同济大学学报：自然科学版，40（5）：757-762.

聂博文，马宏绪，王剑，等，2007.微小型四旋翼飞行器的研究现状与关键技术.电光与控制，14（6）：113-117.

孙杰，林宗坚，2003.无人机低空遥感监测系统.遥感信息（1）：49-50.

唐强，朱志强，王建元，2004.国外无人机自主飞行控制研究.系统工程与电子技术，26（3）：418-422.

王之卓，1979.摄影测量原理.测绘通报，4：016.

张过，刘斌，江万寿，2012.虚拟CCD线阵星载光学传感器内视场拼接.中国图象图形学报，2012，17（6）.

张剑清，潘励，王树根，2003.摄影测量学.武汉：武汉大学出版社.

（本文编辑：袁泽轶）

Study on the coastline orthophoto mosaic using UAV images based on red-black data structure

FAN Shi-yue，ZHANG Feng，LU Wen-hu，WANG Jing，WANG Feng，LIU Qing-qun
（National Marine Data and Information Service，Tianjin 300171，China）

Abstract：With the rapid development of UAV technology，photogrammetric technology involving high resolution camera is widespreadly applied to lots of fields. Compared with traditional survey methods，it is more difficult to handle with aerial images，captured by cameras on unstable aerial platform. In this paper，red-black data structure is used in large scale tie point matching and connecting. Meanwhile the camera calibration and bundle adjustment technologies are used to generate coastline mosaic using UVA images.

Keywords：UAV photogrammetry；image matching for large viewport；red-black data structure；image mosaic

中图分类号：P231.5

文献标识码：A

文章编号：1001-6932（2016）02-0132-08

Doi：10.11840/j.issn.1001-6392.2016.02.002

收稿日期：2015-06-25；

修订日期：2015-08-12

作者简介：范诗玥（1989-），女，硕士，研究实习员，主要从事海岛遥感影像处理及管理研究，电子邮箱：julia317fan@126.com。

通讯作者：张峰（1978-），男，博士，副研究员，电子邮箱：olileo@163.com。