基于熵权法的小样本灰色置信区间估计
杨文光, 吴云洁, 王建敏
(1.华北科技学院 基础部 河北 三河 065201;2.北京航空航天大学 自动化科学与电气工程学院 北京 100191)
基于熵权法的小样本灰色置信区间估计
杨文光1, 2,吴云洁2,王建敏2
(1.华北科技学院 基础部河北 三河 065201;2.北京航空航天大学 自动化科学与电气工程学院北京 100191)
摘要:针对小样本数据的灰色点估计和灰色区间估计问题,将样本误差均值、样本误差标准差引入到灰色距离测度中,改进了已有灰色估计算法.在对小样本数据进行密集扩充过程中,可以提高灰色估计的区分度.该算法利用数据本身分布特点,设计了数据间的灰色距离矩阵,提出了基于熵权法的灰色点估计权重计算方法.最后结合小样本数据进行了参数估计的仿真实例验证,在对小样本数据进行Bootstrap重抽样法作用下进行了不同灰色点估计和区间估计的比较,突出了所提算法的有效性,验证了理论分析结果的正确性.
关键词:灰色估计; 小样本; 熵权法; 区分度
0引言
仿真模型验证是VV&A工作的主要内容,是确保仿真模型可信的重要保证.没有经过验证的模型,是不能据此做出任何有价值的决策.仿真模型的有效性直接影响仿真系统的可信性与仿真结果的应用程度.随着研究的不断深入,复杂系统的仿真可信性验证工作正面临着数据收集困难和模型参数难以确定的问题.考虑到一些系统的实验操作的复杂性和困难性以及实验成本,我们往往只能观测到系统运行的有限数据,即小样本数据.小样本数据可能是系统运行的一些状态,也可能是系统运行参数的有限参考数据.如何通过小样本数据进行仿真系统的可信性验证,以及如何对仿真系统关键参数进行估值,成为仿真可信性验证的主要工作.吴利丰等探讨了离散灰色模型,说明原始序列样本量大小与解的扰动界大小呈正相关性,弱化了原始数据序列的随机性[1].文献[2]利用正态分布小样本相容性理论建立了一种小样本情况下的弹道一致性评定方法,减少了因样本容量小而带来的计算误差.文献[3]研究了复杂系统的环境、功能、状态等因素的随机性,构建了小样本条件下的基于变动统计的复杂系统可靠性综合评估方法,扩大了样本量,提高了评估精度.
参数估计是统计推断的主要组成部分,进行未知参数估值并确定参数估值满足可信度要求的取值区间是确保后续数据处理成功的重要保证.面对复杂的仿真系统,我们往往因实验条件与实验环境的限制,只能获得一些关键节点运行条件下的小样本数据,这给仿真系统的可信性验证带来了一定的障碍.为了保障仿真的顺利进行,提高仿真系统的有效性和精确性就需要进行由小样本数据确定的被估计仿真参数的可信性验证工作.建立在大数定理和分布已知基础之上的传统参数估计方法,对小样本数据的参数估计显得无能为力.小样本作为一个典型的灰色系统[4—5],表现出系统部分信息已知与部分信息未知的特点.当系统存在信息缺失和观测不全等信息不完备情况时,对系统参数的估计就会存在较大的误差,采用贝叶斯网络参数学习算法为解决小样本条件下的模型可信性和有效性提供了一种解决思路[6—7].文献[4]使用小样本数据的拓扑关系和距离关系,定义了灰色距离测度,建立了基于灰色生成的灰色区间估计.文献[5]在分布未知的情况下,基于灰色关联理论和范数理论,给出了反映灰色距离信息量化与平均灰色距离量化的点估计与区间估计算法.文献[8]针对小样本数据的区间估计问题,将Bootstrap重抽样[9—10]引入到灰色估计理论中,对小样本数据进行了重抽样扩充,比较了3种不同灰色区间估计的性能.然而上述文献在具体处理小样本数据时都忽略了样本数据聚集与离散程度对数据关系度量的重要性.
本文考虑到小样本数据分布的密集程度,建立基于数理统计概念的新的灰色距离测度,以便确定包含信息更全面的灰色置信区间,在数据向密集方向变化时具有更好的区分度.对于灰色点估计问题,建立了全面衡量小样本数据稀缺性和有效性的灰色距离矩阵,据此改进熵权法确定更客观的权值.考虑到Bootstrap重抽样是一种重要的数据扩充法,本文引入Bootstrap重抽样,比较重抽样之前之后,采用本文方法所建立的灰色点估计和灰色置信区间的差异性.最后通过实例,验证了本文方法的有效性.
1改进的灰色测度距离
设X={x1,x2,…,xn}为小样本数据,它构成数据样本空间.设x0为被估计参数,下面讨论通过数据样本空间X来确定被估计参数x0的取值区间和取值可信度大小.
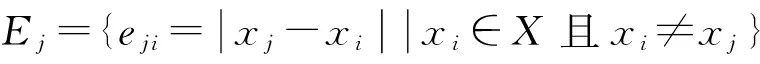
下面选择样本误差均值来表征不同数据间的距离差异,其中xj(j=1,2,…,n)与数据样本空间X的总体距离差异标记为

(1)
为了表示数据xj与X中其他数据的离散与聚集程度的差异性,选择样本误差标准差来表征数据的离散与聚集的程度,描述为

(2)
注1:若总体距离差异ej取值越大,说明xj与X中其他数据的距离差异越大,反之,距离差异越小;若距离差异标准差sj取值越大,则xj与数据样本空间X中其他数据分布越分散,反之,分布越集中.
文献[4]定义的灰色距离测度考虑到了数据xj与数据样本空间总体距离差异问题,却没有反映出数据分布的离散与聚集的程度,鉴于距离差异ej与距离差异标准差sj的相互依存和相互作用关系,下面定义一种新的关于数据样本xj与被估计参数x0间的灰色距离测度
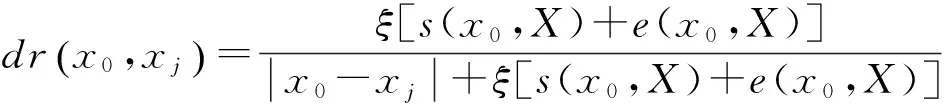
(3)
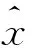
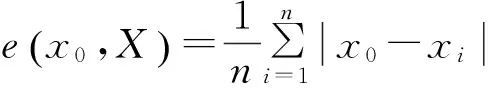
(4)
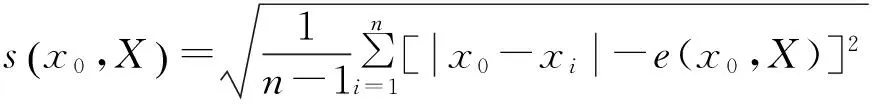
(5)
dr(x0,xj)取值越大,说明xj与x0越接近,当xj=x0时,dr(x0,xj)=1,当dr(x0,xj)取值越小时,说明xj与x0的差异越大.特别地,当xj与小样本数据空间X的数据分布中心越接近,且s(x0,X)取值越小,则xj与x0也就越接近,此时dr(x0,xj)取值越大,反之,则dr(x0,xj)取值越小.文献[4]提出的数据样本xj与被估计参数x0间的灰色距离测度为

(6)
其中:‖d(X,x0)‖}.

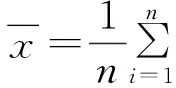
S(X)取值减小时,dr(x0,X)(或dr′(x0,X))的增长量可用于度量其区分度,下面使用V(x0)(或V′(x0))来标记在样本数据空间X的S(X)减小时对应的被估计参数x0关于样本空间X的灰色距离测度区分度.
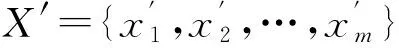
证明由于x0由X确定,x0的真值取值不变,X沿着数据密集方向变化,即在X基础上,获得了更多的数据,生成新的样本数据X′,为X⊂X′.对X′中的数据重新进行排序,X′与X中相同的数据采用相同的标记,新数据顺次进行标记,得X′={x1,x2,…,xn,xn+1,…,xm}.
因为,

(7)

(8)
考虑到,



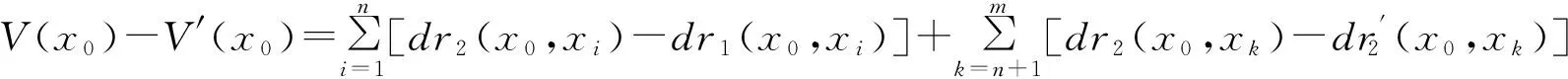
又因为,

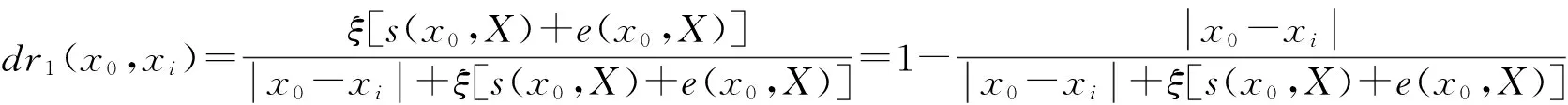
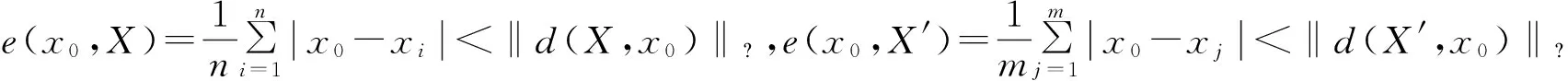
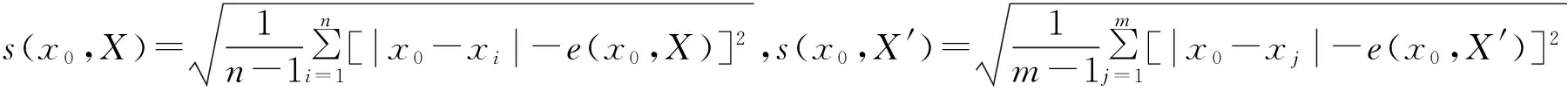
e(x0,X)>e(x0,X′),s(x0,X)>s(x0,X′),i=1,2,…,n,j=1,2,…,m.
所以,


注2:其中V(x0)表示依据公式(3)构建的灰色距离测度的区分度,V′(x0)表示依据公式(6)构建的灰色距离测度的区分度,二者各自代表着相应的灰色距离测度的总和的增长量.
2基于熵权法的灰色估计值计算
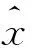
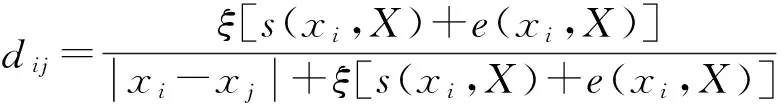
步骤2计算各指标xi的信息熵:
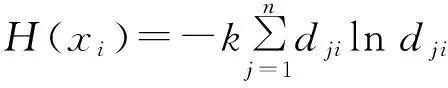
(9)
其中:H(xi)为指标xi的信息熵;k为调节参数,一般取k=1/lnn,i=1,2,…,n.
步骤3计算各指标xi的权重,将评价指标xi的信息熵转化为权重值:

(10)
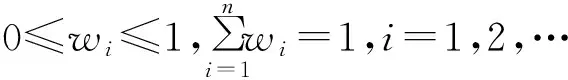
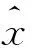
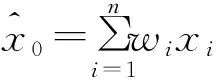
(11)
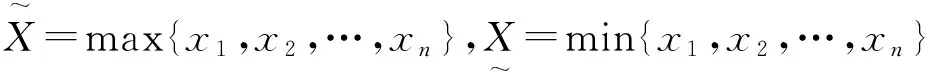
3灰色置信区间的确定
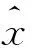
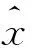

当小样本数据不是完全有效覆盖参数真值取值范围时,则需要对小样本数据进行扩容,使其成为覆盖被估计参数取值范围的完备数据.目前,常见的数据重抽样方法是Bootstrap重抽样法.该方法在无法确定数据样本空间X={x1,x2,…,xn}的确切分布的情况下,通过对X不断的重复有放回抽样,从而获得与X分布相一致的涵盖参数取值的大样本数据.Bootstrap重抽样法是本文所构建的灰色点估计与灰色区间估计的补充.下面在实例验证时将给出区分度明显增大的仿真实例,以佐证定理1.
4实例验证与方法比较
定理1表明新的灰色距离测度是有效的,表现出更好的区分度,据此进行的灰色点估计和灰色区间估计是有效的.下面分别选择能够有效表示参数取值范围的小样本数据在Bootstrap重抽样前后为例进行灰色点估计与区间估计,对灰色区间估计方法做出相应的区分度说明.
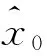
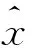

例2使用Bootstrap重抽样法对例1中数据进行Bootstrap重抽样1 000次,与原数据一起构成新的样本数据,并进行灰色点估计和灰色区间估计.
Bootstrap重抽样法是小样本数据较好的数据补充方法,本文获得的灰色估计值与传统数理统计方法计算的样本均值更接近,比较符合大数定律.在使用Bootstrap重抽样法对小样本数据进行密集采集数据情况下,显现出更好的区分度.图2给出了在给定灰色置信度0.95下的灰色置信区间与参数取值之间的关系,表2给出了本文方法与参考文献[4]法采用Bootstrap重抽样法进行灰色估计值、灰色置信区间、区间长度与区分度之间的比较.在选择相同置信度情况下,表1、表2说明本文方法区间长度更短,精度更高,区分度更好.
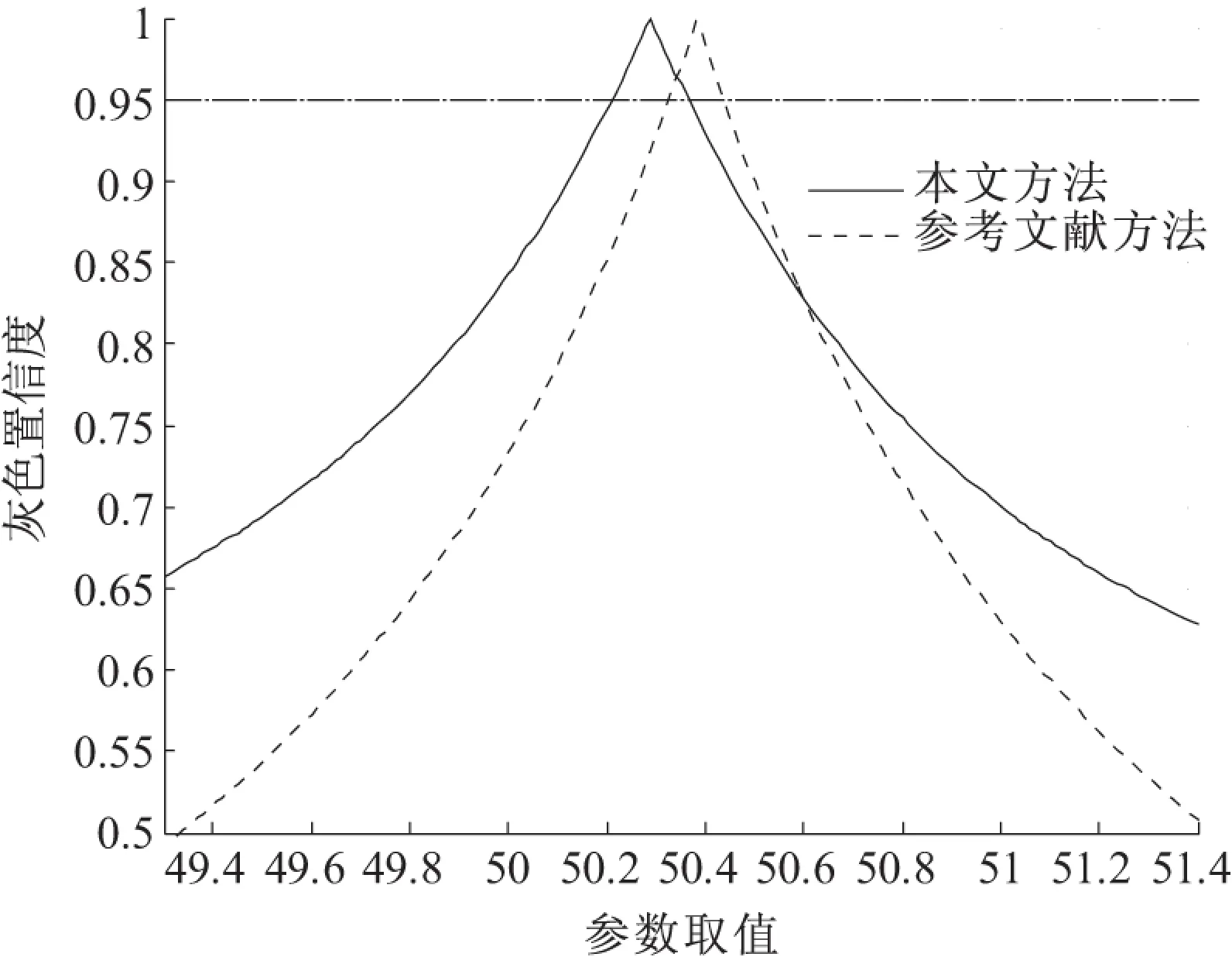
图1 灰色置信度比较Fig.1 The comparison of grey confidence

图2 重抽样下灰色置信度变化曲线比较

方法类型估计值置信区间区间长度数理统计法50.375(50.042,50.711)0.669参考文献法50.3826(50.354,50.411)0.057本文方法50.3763(50.354,50.399)0.045

表2 仿真结果比较(α=0.95)
5结论
在工程实际中,随着处理问题复杂程度和未知因素的增多,有时仅能获得一些参数的小样本数据,据此进行参数的点估计和区间估计就成为一个非常重要的问题.本文从小样本数据本身出发,利用数据间的样本误差均值、样本误差标准差生成了新的灰色距离测度,讨论了算法在数据朝密集方向变化情况下对数据处理的区分度,理论上显示本文算法更有效.在进行灰色点估值时,设计了基于样本数据间内在信息熵关系的样本权重新方法,使得灰色点估值更客观.最后结合小样本数据进行了算法的有效性与正确性的验证工作,结果显示在使用Bootstrap重抽样法对小样本作用前与作用后都是合理的.
参考文献:
[1]吴利丰,刘思峰,姚立根. 基于分数阶累加的离散灰色模型[J]. 系统工程理论与实践, 2014, 34(7): 1822—1827.
[2]张领科,赵峰,余永刚. 一种小样本情况下的弹道一致性评定方法[J]. 兵工学报, 2014, 35(12): 2124—2128.
[3]张海瑞,洪东跑,赵宇,等. 基于变动统计的复杂系统可靠性综合评价[J]. 系统工程与电子技术,2015, 37(5): 1213—1218.
[4]刘义,王国玉,柯宏发. 一种基于灰色距离测度的小样本区间估计方法[J]. 系统工程与电子技术,2008,30(1):116—119.
[5]CHEN Y G, KE H F, LIU Y. Grey distance information approach for parameter estimation of small samples[J]. IEEE transaction on instrumentation and measurement, 2008, 57(6): 1281—1286.
[6]任佳,高晓光,茹伟. 数据缺失的小样本条件下BN参数学习[J]. 系统工程理论与实践,2011, 31(1):172—177.
[7]任佳,高晓光,白勇. 信息不完备小样本条件下离散DBN参数学习[J]. 系统工程与电子技术,2012, 34(8): 1723—1728.
[8]刘恒,梅卫,单甘霖. 小样本数据的三种区间估计方法性能分析[J]. 系统工程与电子技术,2014, 36(10): 1929—1933.
[9]XU L W, YANG F Q, CHEN R R, et al. A parametric bootstrap test for two-way ANOVA model without interaction under heteroscedasticity[J]. Communications in statistics-simulation and computation, 2015, 44: 1264—1272.
[10] PETER A D, EULOGIO P I, JUAN J E. The total bootstrap median: a robust and efficient estimator of location and scale for small samples[J]. Journal of applied statistics, 2015, 42(6): 1306—1321.
(责任编辑:王浩毅)
Grey Confidence Interval Estimation of Small Samples Based on Entropy-weight Method
YANG Wenguang1, 2,WU Yunjie2,WANG Jianmin2
(1.DepartmentofBasic,NorthChinaInstituteofScienceandTechnology,Sanhe065201,China;2.SchoolofAutomationScienceandElectricalEngineering,BeihangUniversity,Beijing100191,China)
Abstract:In order to solve the problem of small samples data of gray estimation and grey interval estimation, the sample average error and sample error standard deviation were introduced into the grey distance measure, and the existing grey estimation algorithm was improved. In the process of intensive expansion of small samples data, the gray degree of the estimation could be improved. Based on the distribution of the data itself, the gray distance matrix of data was designed, and the weight of grey point estimation was proposed. Finally the small samples data of parameter estimation was tested to examing the simulation results. The results highlighted the effectiveness of the proposed algorithm, and verified the correctness of the theoretical analysis .
Key words:grey estimation; small samples; entropy-weight method; distinguish degree
收稿日期:2015-08-29
基金项目:国家自然科学基金资助项目(91216304, 61472137);中央高校基本科研业务费资助项目(3142015022, 3142014127);华北科技学院重点学科项目(HKXJZD201402).
作者简介:杨文光(1981—),男,河北保定人,讲师,博士研究生,主要从事智能信息处理研究, E-mail:yangwenguang@buaa.edu.cn.
中图分类号:N945.13
文献标志码:A
文章编号:1671-6841(2016)01-0051-06
DOI:10.3969/j.issn.1671-6841.201508009
引用本文:杨文光,吴云洁,王建敏.基于熵权法的小样本灰色置信区间估计[J].郑州大学学报(理学版),2016,48(1):51-56.

