可变外场中非线性系统热输运理论与计算方法
石 成,陈 颖,李登峰
(重庆邮电大学 理学院,重庆 400065)
可变外场中非线性系统热输运理论与计算方法
石成,陈颖,李登峰
(重庆邮电大学 理学院,重庆400065)
摘要:可变外场对低维纳米非线性体系热输运的调控研究有利于新型热控制器件的设计。本论文比较分析了用于热输运理论研究的玻尔兹曼方法、格林-库伯方法、非平衡格林函数法和量子主方程的优势和局限性,发现非平衡格林函数方法可处理弱耦合体系在可变外场作用下非线性体系的热输运,4阶量子主方程可处理耦合系数在0.45以内的中等程度耦合体系。
关键词:非线性系统;热输运;非格林平衡函数;量子主方程
伴随“声子学”新兴领域不断发展和微量分析技术和实验测量手段的不断改进[1,2],低维纳米结构的热输运控制受到人们的重视,热输运调控研究有助于解决高集成电子器件的散热问题、改善超高速飞行器以及大功率发动机等高技术装备的隔热问题、寻找热电材料提供清洁能源以及设计高效热控制器件。
众所周知,控制电流的电子二极管、晶体管的发明直接导致了现代半导体产业的诞生,极大地促进了工业技术的进步。如能像控制电流这样灵活的控制热流,将会使“声子学”领域快速发展。由于声子是没有质量且不带电的准粒子,不受重力和电磁力的直接影响,从而控制热流难于控制电流。近几年低维纳米结构热控制研究受到广泛重视,从理论上设计出一些热控制器件模型,比如热整流器、热晶体管、热逻辑门和热存储器等[3];实验中制备出了固态热二极管、多壁碳纳米管的热变阻器、固态热存储器和热晶体管等热控制器件[4]。目前热控制器件大多在稳恒外场作用下调控恒定热流,当可变外场作用于低维纳米结构时,不仅可用于研究暂态过程,而且还可以产生稳恒外场下不可能产生的新的物理现象,比如热泵[5],Berry相引起的热流等。另外,可变外场可以大幅度提高热控制器件的性能,可变门电压使得两极为金属的量子点热电性能提高40%[6],因此,可变外场下热控制研究是“声子学”领域的一个重要分支,有利于新型热控制器件的研究。
1热输运理论研究方法
对于热输运的研究,传统的方法有玻尔兹曼(Boltzmann)方法和格林-库伯(Green-Kubo)方法。玻尔兹曼方法是研究体材料热输运的重要工具,是完全基于扩散输运的理论。但是,纳米结构的声子平均自由程与结构尺寸可比拟时,热输运并不是扩散输运。而且,玻尔兹曼方法完全忽略了量子相干性,然而当退相干长度小于结构尺寸时,量子相干性对微观结构的热输运具有重要作用。因此,玻尔兹曼方法不适应于非线性体系热输运研究。格林-库伯方法基于线性响应理论,能有效计算热导、ZT因子等热输运参数,但它不能处理远离平衡态的体系,难以准确得到非线性体系的延迟格林函数,从而需要附加各种近似方法来处理。因此,传统的热输运研究方法已经不适用于研究非线性体系的热输运。
随着纳米技术的迅速发展,迫切需要发展新的研究微观结构热输运的方法。因此,Landauer公式被广泛的用于描述介观体系中的量子输运过程,它不关心体系的内部特征,将量子输运过程简单的看成载流子的透射,透射率是它主要关心的物理量。Landauer公式最早被用来研究电输运,但它也可以描述声子、光子等其他载流子的介观输运。它帮助人们更好的理解介观体系中的输运,并成功的预测了由弹道输运引起的量子电导和量子热导。Landauer公式能够为介观输运提供简单清晰的物理图像,但它本身无法给出透射率,因此,它必须借助其他方法为其提供透射信息,才能在纳米体系热输运的研究中发挥出更广泛的作用。
过去10年里,非平衡格林函数法(Nonequilibrium Green’s Function Method,NEGF)成为了研究微观结构热输运的一个重要工具[7]。NEGF是一个量子理论,能得到纳米材料的所有量子特性,而且对于线性模型可以精确求解,所以广泛应用于电输运和热输运的研究,但NEGF擅长于处理线性体系,它可处理可变外场作用下线性体系的量子输运,而且可得到精确解。对于非线性体系在可变外场作用下的量子输运,NEGF必须进行微扰处理,因此只能适应于弱耦合情况。Bagchi等人分析了含时可变磁场对一维自旋链热输运的影响[8],把自旋态进行了经典处理,作为矢量,丢失了其中的量子相干性。
对于处理可变外场作用下非线性体系的量子输运,量子主方程(Quantum Master Equation,QME)提供了实现这个目标的可能性[9],它是通过研究热源对微观结构的影响,计算在热源影响下微观结构的约化密度矩阵,从而实现对热流的计算。QME方法是对微观结构本身进行数值精确解,原则上它能有效处理任何非线性体系。但是,目前的大多数QME利用了Markov近似,只能研究稳恒系统。Knezevic等人基于QME研究含时量子输运[10],分析静外场作用于多体量子体系后趋于稳定状态的暂态过程。另外,QME方法只能处理热源与系统之间的弱耦合情况,如要处理强耦合体系,必须引入高阶微扰理论得到高阶QME,基础理论已经初步成型[11],通过引入高阶微扰理论处理中度耦合的热流。图1展示了不同热输运理论研究方法擅长处理的体系。
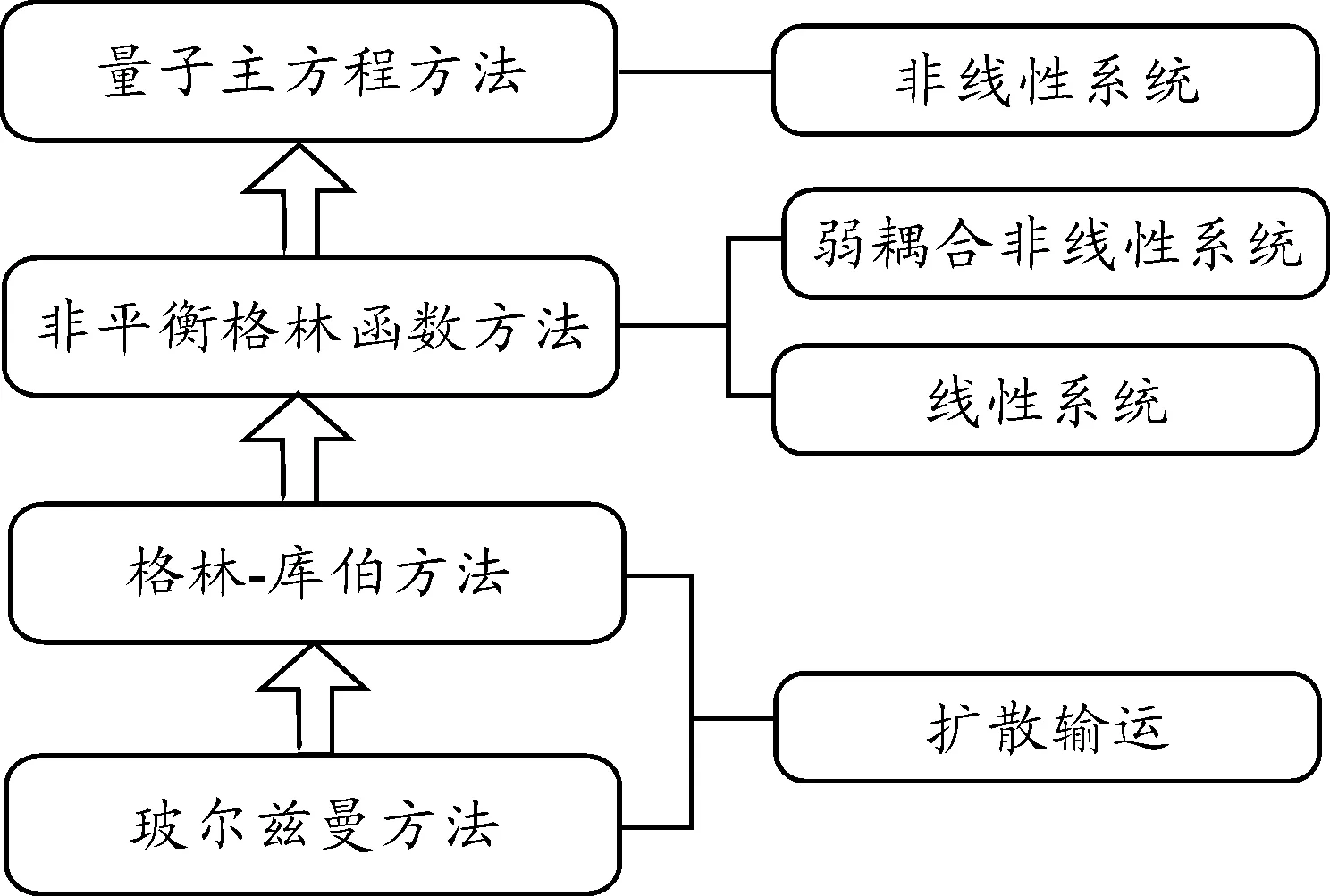
图1 热输运理论研究方法比较
2基本研究方法
基于以上分析可知,处理可变外场对非线性体系的量子输运主要可以通过量子主方程以及弱耦合条件下的NEGF方法。下面对该两种方法进行比较分析。
2.1非平衡格林函数方法
非平衡格林函数是处理非平衡态和相互作用系统最有力的方法。它的理论基础源于量子场理论。 Schwinger、Kadanoff和Baym等人建立了非平衡格林函数早期的公式和理论,其中最有代表的是Keldysh,他创造了著名Keldysh定理,Keldysh图像展开法是一种能处理任意初始态的普适方法[12]。Meir等[13]用此方法研究了通过异质结的电子输运,成功应用于电输运性质的研究之中。非平衡格林函数在热输运中的应用是过去十几年间发展起来的。非平衡格林函数研究了弹道声子输运性质,然而非平衡格林函数的真正优点在原理上能严格处理非线性效应。本文将介绍声子非平衡格林函数的基本理论及其数值实现的方法,图2为热输运示意图。
处理利用非平衡格林函数方法的问题,首先介绍格林函数方面的有关知识。六种实时格林函数,将其定义为
以上6个式子分别表示推迟、前进、大于、小于、时序、反时序格林函数。在海森堡汇景中,U(T)表示粒子位移的组成列矢量。θ(T)表示阶梯函数,定义为
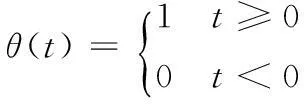
同时,以上6种实时格林函数之间的关系如下
由此发现,以上6式中的3个是线性独立的,选取其中的三式因此就具有很大的任意性。常用的是:① G>,G<一般称其为关联函数,它们与可观察量及其动力学性质 (如态密度,热流等)息息相关; ② Gr,GA考虑其解析性质的良好性,因此用来计算物理的响应,比如散射速率,态密度和声子谱等。

图2 热输运示意图
如果得到了非平衡格林函数,接下来与热输运相关的物理量就相应计算出来,例如声子透射谱、声子态密度、热导、热流等。在处理量子热输运问题中,这些物理量便可以提供详细的物理图像。
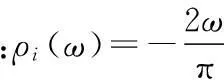
因而,总的声子态密度就表示为:
声子在频率空间和实空间的分布,通过声子态密度和局域态密度来得到,在求解量子热输运的问题中,二者起到至关重要的作用。
热导与声子透射谱分别表示为:
2.2量子主方程方法
目前主方程方法被广泛应用于纳米结构稳流的研究,对这个方法进行拓展和延伸得到含时Redfield QME,不仅能处理任何非线性系统,还能处理纳米结构在任意含时外场下的热输运计算[14]。从含时的哈密顿函数出发,利用含时Redfield QME方法推导随时间改变的约化密度矩阵,从而得到非稳态热流表达式。
传统的主方程方法用到 Markov 近似,只能研究稳态情况,因此利用Markov近似之前的Redfield QME 方法研究任意含时的外场对非简谐体系的热输运影响[15]。总的哈密顿量为:
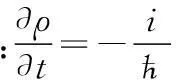
根据矩阵:
可求得热流分布。
以上只适用于较弱的耦合体系,得到的是2阶量子主方程以及2阶热流公式,目前可利用高阶微扰理论得到4阶量子主方程以及4阶热流处理中等程度的耦合。4阶量子主方程
4阶热流公式为:

2.3计算方法的模拟比较分析
图3给出了利用NEGF、2阶和4阶量子主方程(2ndQME和4thQME)得到通过量子点电流与电极和系统之间的耦合系数关系,从图中可以看出,NEGF可以得到精确解,2阶量子主方程仅适合于耦合系数在0.2以内的情况,4阶量子主方程可适用于耦合系数在0.45以内。因此,4阶QME方法能很好处理中等程度耦合时电输运。
图3基于非平衡格林函数法(NEGF)、2阶和4阶量子主方程(2ndQME和4thQME)得到通过量子点电流与电极和系统之间的耦合系数关系。左温度T=0.02(kB/eV),左电极和右电极化学势分别为1.5 eV和0.5 eV,位势能为1 eV。

图3 基于非平衡格林函数法
3结束语
研究外场调控低维纳米非线性体系热输运时不仅能发现新的物理现象,有利于新型热控制器件的研发,而且也是“声子学”的重要分支领域,因此有必要对热输运控制的理论和计算方法进一步研究和总结。本论文在分析热输运研究方法的基础上,重点比较分析了非平衡格林函数、2阶量子主方程和4阶量子主方程,给出每种研究方法的优势和局限性,而且通过模拟计算得到4阶量子主方程可处理耦合系数在0.45以内的中等程度耦合体系。为了处理任意耦合程度的非线性体系在外场作用下的量子输运,需要发展更高阶的量子主方程。研究方法的发展有助于新型热控制器件的设计和实现,从而推动“声子学”领域快速发展。
参考文献:
[1]LI N B,REN J,WANG L,et al.Phononics: Manipulating heat flow with electronic analogs and beyond[J].Rev Mod Phys,2012,84(3):1045-1066.
[2]LEE W,KIM K,JEONG W,et al.Heat dissipation in atomic-scale junctions[J].Nature,2013,498(7453):209.
[3]CHEN X K,XIE Z X,ZHOU W X,et al.Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction[J].Carbon,2016,100: 492-500.
[4]LI S Z,DING X D,REN J,et al.Strain-controlled thermal conductivity in ferroic twinned films[J].Scientific Reports,2014(4):6375.
[5]CHUMPITAZI B P,SHULMAN R J.Underlying molecular and cellular mechanisms in childhood irritable bowel syndrome[J].Molecular and Cellular Pediatrics,2016,3(1):11.
[6]CREPIEUX A,SIMKOVIC F,CAMBON B,et al.Enhanced thermopower under a time-dependent gate voltage[J].Phys Rev B,2011,83(15): 153417.
[7]WANG J S,AGARWALLAB K,LI H,et al.Nonequilibrium Green’s Function method for quantum thermal transport[J].Front Phys,2013,5:1-24.
[8]BAGCHI D,MOHANTYP K.Thermally driven classical Heisenberg model in one dimension[J].Phys Rev B,2012,86(21): 214302.
[9]LU J T,ZHOU H B,JIANG J W,et al.Effects of electron-phonon interaction on thermal and electrical transport through molecular nano-conductors[J].Aip Advances,2015,5(5):053204.
[10]KNEZEVIC I,NOVAKOVIC B.Time-dependent transport in open systems based on quantum master equations[J].J Comput Electron,2013,12(3):363-374.
[11]THINGNA J,ZHOU H B,WANG J S.Improved Dyson series expansion for steady-state quantum transport beyond the weak coupling limit: Divergences and resolution[J].J Chem Phys,2014,141(19):194101.
[12]WANG J S,AGARWALLA B K,LI H N,et al.Nonequilibrium Green’s Function Method for quantum thermal transport[J].Frontiers of Physics,2014,9(6): 673-697.
[13]DAS S G,DHAR A.Landauer formula for phonon heat conduction: relation between energy transmittance and transmission coefficient[J].European Physical Journal B,2012,85(11):372.
[14]ARRIGONI E,KNAP M,VON DER LINDEN W.Nonequilibrium dynamical mean-field theory: An auxiliary quantum master equation approach[J].Physical Review Letters,2013,110(8):086403.
[15]ZHOU H B,THINGNA J,WANG J S,et al.Thermoelectric transport through a quantum nanoelectromechanical system and its backaction[J].Physical Review B,2015,91(4):045410.
(责任编辑杨继森)
本文引用格式:石成,陈颖,李登峰.可变外场中非线性系统热输运理论与计算方法[J].兵器装备工程学报,2016(5):161-164.
Citation format:SHI Cheng,CHEN Ying,LI Deng-feng.Research on Theory and Calculation Method of Thermal Transport for Nonlinear Systems via Time-Varying External Fields[J].Journal of Ordnance Equipment Engineering,2016(5):161-164.
Research on Theory and Calculation Method of Thermal Transport for Nonlinear Systems via Time-Varying External Fields
SHI Cheng,CHEN Ying,LI Deng-feng
(College of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
Abstract:Research on effective control of thermal transport via time-varying external fields for nonlinear systems is beneficial to design the novel thermal control devices.In this paper,we made a comparative analysis for the theoretical research methods of Boltzmann method,Green-Kubo method,nonequilibrium Green’s function method and quantum master equation.We gave the superiority and limitation of them.It is found that the nonequilibrium Green’s function method can deal with the thermal transport of weak-coupling system under the time-varying external fields.The 4-order quantum master equation can study the middle-coupling system when the coupling coefficient is less than 0.45.
Key words:nonlinear system; thermal transport; nonequilibrium Green’s function method; quantum master equation
doi:【基础理论与应用研究】10.11809/scbgxb2016.05.038
收稿日期:2015-12-20;修回日期:2016-01-15
基金项目:国家青年自然科学基金(11504038)
作者简介:石成(1990—),男,硕士研究生,主要从事低维纳米材料输运性质研究。
中图分类号:O471.4
文献标识码:A
文章编号:2096-2304(2016)05-0161-04

