一种混合动力电动汽车电池荷电状态预测的新方法

王　琪　孙玉坤　倪福银　罗印升

(1.江苏理工学院电气信息工程学院　常州　213001 2.南京工程学院电力工程学院　南京　211167 3.江苏大学机械工业设施农业测控技术与装备重点实验室　镇江　212013)



一种混合动力电动汽车电池荷电状态预测的新方法

王琪1，3孙玉坤2，3倪福银1，3罗印升1

(1.江苏理工学院电气信息工程学院常州213001 2.南京工程学院电力工程学院南京211167 3.江苏大学机械工业设施农业测控技术与装备重点实验室镇江212013)

摘要针对混合动力电动汽车(HEV)电池荷电状态(SOC)预测问题，引入贝叶斯极限学习机(BELM)方法。对极限学习机和贝叶斯线性回归的基本原理进行详细介绍，为提高极限学习机的拟合和泛化能力，采用贝叶斯方法来优化极限学习机输出层的权重。在循环工况条件下选择电池的工作电压、工作电流和表面温度参数用来预测电池SOC的实时值，同时兼顾HEV再生制动时的能量回馈过程。高级车辆仿真软件ADVISOR下的仿真结果和实际实验结果均表明：所设计的预测模型具有较高的准确度，能够实时准确地预测出SOC值，实用性强且有效性高。

关键词：贝叶斯极限学习机混合动力电动汽车荷电状态

0引言

电池作为混合动力电动汽车动力系统的关键部件，对整车系统的动力性、安全性以及经济性至关重要[1]。为保证电池性能良好，延长其使用寿命，需要对电池进行合理的管理与控制，但是前提必须是准确而又可靠地获得电池的荷电状态(State Of Charge，SOC)[2]。SOC作为电池的内部特性不可以直接对其进行测量，只能通过对电池电压、电流和温度等一些直接测量的外部特性参数预测而得。

SOC表征电池的剩余容量，其值为剩余电量与电池放电到截止电压时的总电量的比值[3]。常用的电池SOC预测方法主要可以归纳为三类，第一类是直接根据电池的电压、电流或者内阻来对SOC进行预测，主要的方法有开路电压法[4]、安时计量法[5]和内阻特性法[6]。这类方法操作简单，但是由于电池电压、电流或内阻与SOC的关系不稳定，因此这一类方法通常都存在预测准确度不高的缺陷。第二类是基于卡尔曼滤波器递推算法的预测方法，卡尔曼滤波法将电池看作动态系统，SOC作为系统内部的一个状态量，该方法预测准确度相对于第一类方法有所提高，但是该方法需要选择动态系统的描述方程，递推过程也涉及到复杂的矩阵求逆运算。同时，卡尔曼滤波器作为递推算法，对初值的选择十分敏感，错误的初值会导致预测结果的不断恶化[7]。第三类是基于RBF核函数神经网络和最小二乘支持向量机[8，9]的预测方法，最小二乘支持向量机(Least Square Support Vector Machines，LS-SVM)也是神经网络的一种，它将结构风险最小化原则[10]应用于神经网络中，目前研究得最多。第三类方法存在的主要问题是训练速度慢，容易陷入局部极小点以及对学习率的选择过于敏感[11]。

针对上述方法存在的缺陷，极限学习机(Extreme Learning Machine，ELM)提供了有效的解决方案。ELM是由新加坡南洋理工大学黄广斌教授提出的一种新的单隐含层前向神经网络(Single hidden Layer Feed-forward neural Network，SLFN)的学习机[12]。ELM网络结构简单、学习速度快而且泛化性能好，利用Moore-Penrose广义逆求解网络权重，可以随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元的个数，便可以获得唯一的最优解。贝叶斯极限学习机(Bayesian Extreme Learning Machine，BELM)是基于贝叶斯线性回归原理来优化极限学习机输出层的权重，它涵盖了贝叶斯模型和ELM的全部优点，降低了计算成本，避免了通过引导等繁琐的方法建立置信区间。

本文采用BELM方法对混合动力电动汽车电池进行SOC的预测，在高级车辆仿真软件ADVISOR下进行仿真，并在实际应用中进行实验验证，两种结果均证明了BELM的有效性。

1极限学习机基本原理

极限学习机属于单隐含层前向神经网络，其网络示意图如图1所示。

图1　极限学习机网络示意图Fig.1　The network diagram of ELM

(1)

式中，wj为连接第j个隐含层结点的输入权值向量，wj=[w1j,w2j,…,wnj]；bj为第j个隐含层神经元的阈值；βj为连接第j个隐含层节点的输出权值向量，βj=[βj1,βj2,…,βjm]T，； wj·xi表示wj与xi的内积；g(x)为隐含层神经元的激活函数[13]。

根据式(1)可以得到一个含N个方程的线性方程为

Hβ=Y

(2)

其中，隐含层输出矩阵

(3)

β=[β1,β2,…,βL]T

Y=[y1,y2,…,yN]T

对于隐含层输出矩阵H，若L≤N，则H以概率1列满秩。同时，黄广斌教授等还指出，对于绝大多数问题，都有L≤N。

所以，输出层参数β可以由式(2)的极小2-范数最小二乘解得

β=H+Y

(4)

式中，H+为H的Moore-Penrose广义逆矩阵。

ELM算法实际上就是一种“回归”表述，在处理分类问题时，ELM是采用多输出回归算法来实现的[14]。

2贝叶斯线性回归原理

贝叶斯极限学习机是基于贝叶斯线性回归原理来优化极限学习机输出层的权重。任何贝叶斯模型的实现都是分为两步[15]：

(1)推断出模型参数的后验分布，这里，模型的前验分布与似然函数的乘积是成比例的。

P(W/D)=P(W)P(D/W)

式中，W为自由参数；D为数据空间。

(2)对于一个新的输入xnew，计算出模型的输出分布ynew(为简单起见，这里只考虑一个输出)，被定义w的后验分布的积分。

P(ynew/xnew,D)=∫P(ynew/xnew,W)P(W/D)dW

(5)

通过式(5)就可以预测出模型的输出[16]。

一般线性模型可以表示成

y=htx+ε

(6)式中，ε服从均值为0、方差为σ2的正态分布N(0;σ2)，上角标“t”为变量h的维数。 式(6)中的条件分布为

P(y/x,h,σ2)=N(ht·x;σ2)

(7)

在大多数应用中，参数分布为

P(h/α)=N(0;α-1I)

(8)

式中，I为单位矩阵；α为一个超参数。假设参数的前验分布、后验分布以及似然函数均按照高斯分布，均值M和方差S可以定义为[17]

M=α-2SXTy

(9)

S=(αI+σ-2XTX)-1

(10)

式中，X、y分别表示为模型的输入向量矩阵和输出向量矩阵，X=[x1,x2,…,xN]，y=[y1,y2,…,yN]。

需要注意的是，式(9)中正则化参数α是高斯方法的一个自然结果。另外，式(9)和式(10)中的参数是通过ML-Ⅱ[18]方法或者证据过程方法[19]进行迭代优化。式(9)～式(13)是一个反复迭代的过程，其中N是参数的数目，P是模型的数目。

γ=N-αtrace[S]

(11)

(12)

(13)

整个迭代过程止于当范数m的差值小于某一个给定值。参数的后验分布可以应用到式(8)中，从而获得在给定输入xnew条件下的输出ynew。

输出服从分布

P(ynew/y,α,σ2)=N(hTxnew;σ2(xnew))

(14)

其中

贝叶斯方法使用了一些超参数的正则化，正则化项可以从模型参数的分布中得到，这样有助于减少模型的过度拟合；另外，置信区间的使用提高了模型输出的可靠性。

本文采用贝叶斯极限学习机实现混合动力电动汽车动力电池SOC的预测，因此贝叶斯极限学习机的输入x则为电池电压、电流和温度等参数，而输出y则为SOC。

3仿真

3.1仿真样本数据采集

HEV电池参数包括电压、电流和温度，采用ADVISOR软件来获取这些参数。ADVISOR是美国能源实验室开发的高级车辆仿真软件，该软件提供了电动车各个部件的模块，使用这些模块便可以搭建虚拟混合动力电动汽车实验平台，同时该软件还提供了使用标准测试路程的模拟行驶程序，可以获取车辆在行驶中的各项参数[20]。文中混合动力电动汽车是使用铅酸蓄电池的标准车型，整车质量1 919 kg，满载2 219 kg，电机额定功率58 kW，电池单体容量16 A·h，额定电压12 V，28个串联，总电压336 V。模拟行驶程序使用的测试工况选择美国城市动态循环驱动工况，该工况广泛使用于混合动力电动汽车性能测试，具有很强的代表性。开发后的混合动力电动汽车电池性能仿真结果如图2所示，SOC真实值的计算方法按照引言中其基本定义求得。另外，由于混合动力电动汽车的再生制动过程会对电池进行能量回馈，因此图2中电池SOC曲线不时会有小幅上升的趋势。

图2　仿真中的电池性能参数Fig.2　The simulation parameters of battery performance

3.2仿真样本数据预处理

模拟测试工况被循环执行了2次，混合动力电动汽车总共行驶了2 740 s。在模拟行驶过程中，使用频率为1的采样速度对电池各项参数进行了记录，采集值包括电池电压、电流、温度和内阻，同时计算出SOC真实值，总共获得2 740组、13 700个数据。为了充分验证预测模型的有效性，对循环执行获得的样本数据进行排列，将第一次循环执行样本中的奇数项数据用于训练，第二次循环执行样本中的偶数项数据进行测试。

另外对于多参数问题的分析与计算，参数的基本度量单位首先要统一，这个观点同样适用于BELM。用于训练的样本数据集首先要被归一化，然后才能用于模型的训练[3]。另外，归一化的数据也有利于加快训练网络的收敛速度。本文使用的归一化方式是将原始数据处理为均值为0、方差为1的新数据。

3.3仿真分析

取电池的电压、电流和温度作为BELM的输入，输出为电池的SOC预测值。为了充分体现BELM的优越性，与当前研究得较多的LS-SVM进行比较研究。BELM的隐含层神经元的个数设置为30，考虑到LS-SVM正则化系数c和核参数σ2的选择会对预测结果产生较大的影响，采用贝叶斯证据框架(Bayesian Evidence Framework，BEF)算法优化LS-SVM(BEF-LS-SVM)，BEF的优化路径采用单纯形法。两种方法的预测步骤如下：

(1)确定电池SOC预测建模所需的输入、输出变量。

(2)采集输入、输出样本数据，归一化处理后，建立用于训练和测试BELM(BEF-LS-SVM)模型的输入、输出样本集。

(3)利用训练样本集对BELM(BEF-LS-SVM)模型进行训练，得到最佳参数。

(4)使用训练好的BELM(BEF-LS-SVM)模型对测试样本集进行一步或者多步预测，输出最佳预测结果。

(5)对预测结果作反归一化处理，计算预测误差。

根据以上步骤，两种方法的预测结果如图3和图4所示。

从图3和图4中不难看出，BEF-LS-SVM预测模型在起始和末端时刻的预测能力较好，而在中间时刻预测能力较差，这是由于中间时刻能量回馈比较频繁，SOC的变化趋势不断地发生改变，BEF-LS-SVM预测模型未能及时响应；BELM的预测效果明显优于BEF-LS-SVM，其预测值与真实值咬合得更加紧密。另外，尽管电池存在能量回馈的现象，BELM的预测模型依然具有较高的跟踪性能。

图3　基于BEF-LS-SVM的仿真预测结果Fig.3　The simulation prediction results based on BEF-LS-SVM

图4　基于BELM的仿真预测结果Fig.4　The simulation prediction results based on BELM

3.4仿真模型评价

为了进一步说明BEF-LS-SVM和BELM所建预测模型的优劣，将预测模型的运行时间、预测值和真实值的方均误差(Mean Squared Error，MSE)、绝对误差(Absolute Error，AE)和相对误差(Relative Error，RE)作为评价指标来评价模型，其中方均误差主要评价预测模型的整体性能，而绝对误差和相对误差主要衡量预测模型的局部性能。MSE、AE和RE的定义为

(15)

(16)

(17)

表1为两种预测模型的方均误差值和运行时间，尽管两者的方均误差值都很小，但是BEF-LS-SVM的误差值是BELM的100倍，这充分说明了基于BELM的SOC预测模型的整体性能非常好。另外，从运行时间上来看，BELM的运行时间约为BEF-LS-SVM的1/4，响应速度快。

表1　仿真中两种预测模型的方均误差和运行时间比较

两种方法的相对误差和绝对误差如图5和图6所示。从图5和图6中可以发现，不管是绝对误差还是相对误差，BELM预测模型的误差最大值均约为BEF-LS-SVM预测模型的1/3，误差分布得更加紧密，因此BELM预测模型的局部性能更加优越。

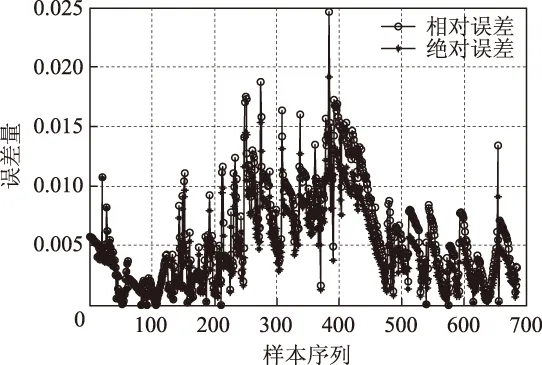
图5　基于BEF-LS-SVM的仿真预测误差Fig.5　The simulation errors based on BEF-LS-SVM

图6　基于BELM的仿真预测误差Fig.6　The simulation errors based on BELM

4实验

4.1实验样本数据采集

为了体现BELM方法的实用性，对该方法进行了实验验证。选用南京汽车集团正在研制的某款混合动力电动汽车样车，整车质量1 450 kg，满载2 490 kg，电机额定功率50 kW。为获得较宽的电池SOC变化范围，样车搭载的铅酸电池单体容量为20 A·h，额定电压12 V，28个串联，总电压336 V。测试工况选择为中国定远汽车实验场中的某段路况，采集的样本数据包括电池电压、电流和温度，并对实测SOC值进行计算，如图7所示。

图7　实验中的电池性能参数Fig.7　The experiment parameters of battery performance

4.2实验样本数据预处理

将工况循环执行了两次，混合动力电动汽车总共行驶了548 s，以10 Hz的采样频率采集电池的性能参数，共获得5 480组、27 400个数据。与仿真分析中的数据处理方法类似，对循环执行获得的样本数据进行排列，将第一次循环执行样本中的奇数项数据用于训练，第二次循环执行样本中的偶数项数据进行测试，数据在训练和预测时同样需要进行归一化处理。

4.3实验分析

按照3.3节中预测步骤，对实验中的电池SOC进行预测，BEF-LS-SVM和BELM的预测结果分别如图8和图9所示。

图8　基于BEF-LS-SVM的实验预测结果Fig.8　The prediction results based on BEF-LS-SVM in experiment

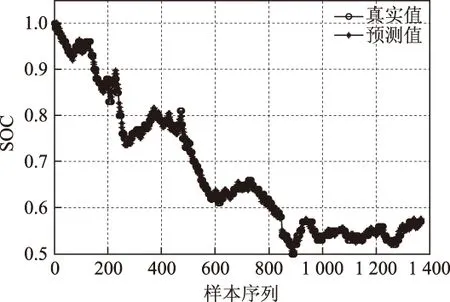
图9　基于BELM的实验预测结果Fig.9　The prediction results based on BELM in experiment

对比图8和图9 中BEF-LS-SVM和BELM的实验预测结果，可以得到与仿真分析中相同的结论：BEF-LS-SVM模型的预测结果明显不如BELM，究其原因还是当HEV处于制动模式下，再生制动能量回馈给电池，其SOC的变化趋势与供能模式下完全相反，BEF-LS-SVM预测模型及时响应性能差；而BELM依然表现出了良好的跟踪性能，其真实值与预测值的偏离程度较小。

4.4实验模型评价

同样选择运行时间、方均误差、相对误差和绝对误差来对两种预测模型的试验结果进行评价，见表2且如图10、图11所示。表2中BEF-LS-SVM的方均误差为BELM的250倍，BELM的整体预测性能较好。从运行时间来看，在实验过程中由于预测数据量增大，BELM预测模型的运行时间与仿真过程基本相同，而BEF-LS-SVM的运行时间却有所增大，这充分体现了BELM学习速度快的优点。对于相对误差和绝对误差，BELM的预测准确度明显高于BEF-LS-SVM，泛化性能较好。

表2　实验中两种预测模型的方均误差和运行时间比较

图10　基于BEF-LS-SVM的实验预测误差Fig.10　The experiment errors based on BEF-LS-SVM

图11　基于BELM的实验预测误差Fig.11　The experiment errors based on BELM

需要注意的是，对比仿真和实验的结果，不难发现，相比于仿真研究，实验过程中两种预测模型的预测准确度有所降低(具体可从相对误差和绝对误差两个评价指标看出)，导致这种情况的主要原因是：

(1)仿真过程中HEV的各个功能模块在建模和参数计算时都是按照理想情况来执行的，忽略了一些实际客观情况和随机因素。

(2)实验过程中参数的采集时间间隔较仿真中要长，这可以从实验中的电池温度参数看出，虽然在HEV整个运行过程中温度也是处于不断上升的趋势，但是其幅度是一个不断变化的值，这对电池SOC的精确预测带来了不少影响。尽管如此，实验过程中BELM的相对误差仅为3.5%，低于5%，符合实际应用。

5结论

本文针对混合动力电动汽车电池SOC预测问题，提出了一种应用于混合动力电动汽车电池SOC预测的贝叶斯极限学习机方法，并对该方法进行了仿真和实验验证，得到如下结论：

1)采用贝叶斯极限学习机对混合动力电动汽车电池的SOC预测是可行的，且模型预测性能良好。

2)考虑到混合动力电动汽车的能量回馈，所建立的预测模型依然具有较高的预测准确度，主要表现为在实验过程中预测系统运行时间短，仅为2 s左右；方均误差小，约为5.25×10-5；并且最大相对误差和绝对误差也仅为3.5%，低于5%，满足实际应用要求。

3)仿真和实验验证的结果一致，贝叶斯极限学习机方法有效性高且实用性强。

参考文献

[1]陈健美，钱承，李玉强，等.基于LS-SVM的混合动力镍氢电池组SOC预测[J].中南大学学报(自然科学版)，2013，44(1)：135-139.

Chen Jianmei，Qian Cheng，Li Yuqiang，et al.SOC prediction of MH/Ni battery in hybrid vehicle based on LS-SVM[J].Journal of Central South University(Science and Technology)，2013，44(1)：135-139.

[2]雷肖，陈清泉，刘开培，等.电动车蓄电池荷电状态估计的神经网络方法[J].电工技术学报，2007，22(8)：155-160.

Lei Xiao，Chen Qingquan，Liu Kaipei，et al.Battery state of change estimation based on neural-network for electric vehicles[J].Transactions of China Electrotechnical Society，2007，22(8)：155-160.

[3]雷肖，陈清泉，刘开培，等.电动车电池SOC估计的径向基函数神经网络方法[J].电工技术学报，2008，23(5)：81-87.

Lei Xiao，Chen Qingquan，Liu Kaipei，et al.Radial-based-function neural network based SOC estimation for electric vehicles[J].Transactions of China Electrotechnical Society，2008，23(5)：81-87.

[4]刘金枝，杨鹏，李练兵.一种基于能量建模的锂离子电池电量估算方法[J].电工技术学报，2015，30(13)：100-107.

Liu Jinzhi，Yang Peng，Li Lianbing.A method to estimate the capacity of the Lithium-ion battery based on energy medel[J].Transactions of China Electrotechnical Society，2015，30(13)：100-107.

[5]于海芳，逯仁贵，朱春波，等.基于安时法的镍氢电池SOC估计误差矫正[J].电工技术学报，2012，27(6)：12-18.

Yu Haifang，Lu Rengui，Zhu Chunbo，et al.State of charge estimation calibration for Ni-MH battery based on ampere-hour method[J].Transactions of China Electrotechnical Society，2012，27(6)：12-18.

[6]Alvarez Anton J C，Garcia Nieto P J，Blanco Viejo C，et al.Support vector machines used to estimate the battery state of charge[J].IEEE Transactions on Power Electronics，2013，28(12)：5919-5926.

[7]高明煜，何志伟，徐杰.基于采样点卡尔曼滤波的动力电池SOC估计[J].电工技术学报，2011，26(11)：161-167.

Gao Mingyu，He Zhiwei，Xu Jie.Sigma point Kalman filter based on SOC estimation for power supply battery[J].Transactions of China Electrotechnical Society，2011，26(11)：161-167.

[8]Lee D T，Shiah S J，Lee C M，et al.State of charge estimation for electric scooters by using learning mechanisms[J].IEEE Transactions on Vehicular Technology，2007，56(2)：544-556.

[9]朱志莹，孙玉坤.群优化支持向量机的磁轴承转子位移预测模型[J].中国电机工程学报，2012，32(33)：118-123.

Zhu Zhiying，Sun Yukun.Predictive modeling of rotor displacement for magnetic bearing using particle swarm optimized-least squares support vector machines[J].Proceedings of the CSEE，2012，32(33)：118-123.

[10]Vapnik V N.The nature of statistical learning theory[M].New York：Springer-Verlag，1999.

[11]张承慧，李珂，崔纳新，等.混合动力电动汽车能量及驱动系统的关键控制问题研究进展[J].山东大学学报(工学版)，2011，41(5)：1-8.

Zhang Chenghui，Li Ke，Cui Naxin，et al.Research progress on key control problems arising from the energy and driving system of the hybrid electric vehicle[J].Journal of Shandong University (Engineering Science)，2011，41(5)：1-8.

[12]Huang G B，Zhu Q Y，SIEW C K.Extreme learning machine：theory and application[J].Neurocomputing，2006，70(1-3)：489-501.

[13]Huang G B，SIEW C K.Extreme learning machine：RBF network case[C]//Proceedings of the IEEE 8th International Conference on Control，Automation，Robotics and Vision，Kunming，2004：1029-1036.

[14]刘学艺，李平，郜传厚.极限学习机的快速留一交叉验证算法[J].上海交通大学学报，2011，45(8)：1140-1145.

Liu Xueyi，Li Ping，Gao Chuanhou.Fast leave-one-out cross-validation algorithm for extreme learning machine[J].Journal of Shanghai Jiaotong University，2011，45(8)：1140-1145.

[15]Congdon P.Bayesian statistical modelling[M].New York：Wiley，2006.

[16]Bishop C.Pattern recognition and machine learning[M].NewYork：Springer-Verlag，2006.

[17]Chen T，Martin E.Bayesian linear regression and variable selection for spectroscopic calibration[J].Analytica Chimica Acta，2009，631(1)：13-21.

[18]Berger J O.Statistical decision theory and Bayesian analysis[M].New York：Springer-Verlag，1985.

[19]MacKay D J C.Probable networks and plausible predictions-a review of practical Bayesian methods for supervised neural networks[J].Network Computation in Neural Systems，1995，6(3)：469-505.

[20]雷肖，陈清泉，刘开培，等.电动车蓄电池荷电状态估计的支持向量机方法[J].中国电机工程学报，2008，28(18)：114-118.

Lei Xiao，Chen Qingquan，Liu Kaipei，et al.Support vector machine based SOC estimation for electric vehicles[J].Proceedings of the CSEE，2008，28(18)：114-118.

作者简介

王琪男，1987年生，博士，研究方向为混合动力汽车复合电源能量管理系统关键技术。

E-mail：wangqitz@163.com(通信作者)

孙玉坤男，1958年生，教授，博士生导师，研究方向为特种电机运行控制及新能源汽车关键技术。

E-mail：syk@ujs.edu.cn

A New Method of Battery State of Charge Prediction in the Hybrid Electric Vehicle

Wang Qi1，3Sun Yukun2，3Ni Fuyin1，3Luo Yinsheng1

(1.School of Electrical and Information EngineeringJiangsu University of Technology Changzhou213001China 2.School of Electrical EngineeringNanjing Institute of TechnologyNanjing211167China 3.Key Laboratory of Facility Agriculture Measurement and Control Technology and Equipment of Machinery IndustryJiangsu UniversityZhenjiang212013China)

AbstractIn order to predict the battery’s state of charge (SOC) in the hybrid electric vehicles (HEV)，the Bayesian extreme learning machine (BELM) is utilized.The basic principles of the extreme learning machine and the Bayesian linear regression are introduced in detail.To improve the abilities of fitting and generalization of the ELM，the Bayesian linear regression is used to optimize the weights of the output layer.The working voltage，the current，and the surface temperature of the battery are chosen to predict the real-time value of SOC under the driving cycle.At the same time，the energy feedback process is taken into account when the HEV is under regenerative braking model.Both the simulation results under ADVISOR and the experimental results indicate that the proposed prediction model has higher predicted accuracy and can achieve real-time and accurate SOC prediction.

Keywords：Bayesian，extreme learning machine，hybrid electric vehicles，state of charge

中图分类号：TM912

国家自然科学基金(51377074)、江苏省优势学科建设工程项目(苏政办发[2011]6号)、江苏省自然科学基金青年基金(BK20150246)、江苏高校自然科学基金(15KJB470004)和江苏理工学院人才引进项目(KYY15009)资助。

收稿日期2015-06-17改稿日期2015-09-06