LF-RH工艺生产超低硫钢钢水温度预报模型

樊智勇，熊　玮，胡汉涛，黄翼飞

(1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081；2.宝钢集团中央研究院，上海，201900)



LF-RH工艺生产超低硫钢钢水温度预报模型

樊智勇1，熊玮1，胡汉涛2，黄翼飞1

(1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉，430081；2.宝钢集团中央研究院，上海，201900)

摘要：根据LF-RH精炼超低硫钢的工艺流程，基于冶金热力学、传热和热量平衡等原理，同时考虑钢包的热状态，建立出钢至浇注过程中的钢水温度预报模型。通过该模型可以得到不同时刻钢水温度和钢包内衬温度的分布曲线。实例验证结果显示，模型计算值与实测值的平均误差为5.6 ℃，误差在±8 ℃以内的占87.5%。另外，运用该模型分析了钢包热状态、出钢过程、传运时间、RH真空室内壁温度等因素对钢水温度的影响规律，可为超低硫钢精炼工艺的优化提供参考。

关键词：LF-RH精炼；钢水温度；预报模型；超低硫钢；热平衡；传热

RH炉和LF炉是现代炼钢厂的标准精炼装备，其生产节奏的快慢直接影响炼钢生产效率[1]。采用LF-RH工艺生产市场需求量较大的高等级管线钢、IF钢等超低硫钢种时，精炼处理时间较长，精炼过程中钢水温度的准确预报对优化操作工艺、降低成本、最大限度地缩短精炼炉处理周期有重要意义。

本文结合宝山钢铁股份有限公司(以下简称宝钢)一炼钢厂实际生产超低硫钢的工艺条件，基于冶金热力学、传热和热量平衡等原理，同时考虑钢包热状态，建立出炉后至浇注过程中的钢水温度预报模型，以掌握从出钢至浇注结束时钢液的温度变化情况，为高效精炼工艺的开发提供参考。

1模型的建立

1.1计算流程及钢包初始热状态的确定

根据超低硫钢精炼处理路径，模拟计算流程为：上一炉钢浇注完毕→空包修整→钢包烘烤→空包待钢→钢包装钢→满包传运→LF精炼→LF精炼后传运→RH精炼→RH精炼后喂线吹氩→传运待浇→浇注。

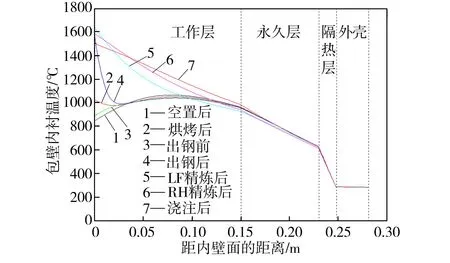
钢水在出钢和盛钢过程中的温度变化受钢包热状态的影响较大，通过在钢包内衬埋入热电偶对宝钢一炼钢厂300 t钢包进行现场热状态测试，结果表明新包投入运转4～6个周期后，包衬内各测试点的温度在同一工序位置基本不变。根据实测结果将浇注完毕时刻的钢包内表面温度设为1400 ℃、外壳温度设为300 ℃，按第一类边界条件下的一维稳态导热处理，得到包壁和包底的温度分布曲线，如图1所示，计算得到的钢包内衬温度与实测点温度基本吻合。

(a)钢包壁

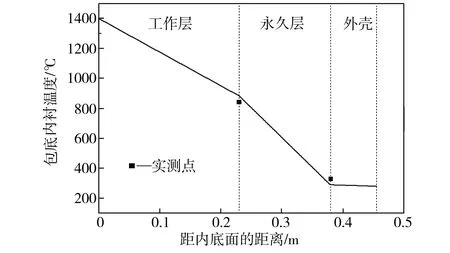
(b)钢包底

Fig.1 Temperature distribution curves of the ladle lining at the end of pouring

1.2钢包衬传热模型

因钢包的壁高远大于壁厚，将包壁看作无限长圆筒，只考虑径向热流；因钢包直径远大于包底厚度，将包底看作薄圆板，只考虑轴向热流。包壁和包底的内部温度变化通过求解非稳态热传导方程式(1)～式(4)得到。

包壁的热传导方程为：

(1)

其边界条件和初始条件如下:

(2)

包底的热传导方程为:

(3)

其边界条件和初始条件如下:

(4)

式中：T壁、T底为钢包包壁和包底内衬温度，K；τ为时间，s；ρ壁、ρ底为包壁和包底的密度，kg/m3；Cp壁、Cp底为包壁和包底的定压比热容，J/(kg·K)；r、z为包壁半径和包底厚度，m；λ壁、λ底为包壁和包底的导热系数，W/(m·K)；α壁外、α底外为包壁和包底外表面综合换热系数，W/(m2·K)；T(r壁外)、T(z底外)分别为包壁和包底的外表面温度，K；T环为环境温度，K；q壁内、q壁外为通过包壁内、外表面的热流密度，W/m2；q底内、q底外为通过包底内、外表面的热流密度，W/m2。模型中考虑了耐火材料热传导率和比热容随温度的变化。

空包阶段包壁、包底内表面热流计算如图2所示。包壁内表面、包底内表面与包口面(有包盖时为包盖的内壁面，无包盖时将包口面看作温度为环境温度的黑体表面)构成一封闭热交换空间。钢包内壁面、内底面和包盖内表面(用下标i=1、2、3区分)中每一个面上的辐射总热流量，即有效辐射Ji都由自辐射Ei和反射部分(1-εi)Gi所组成：

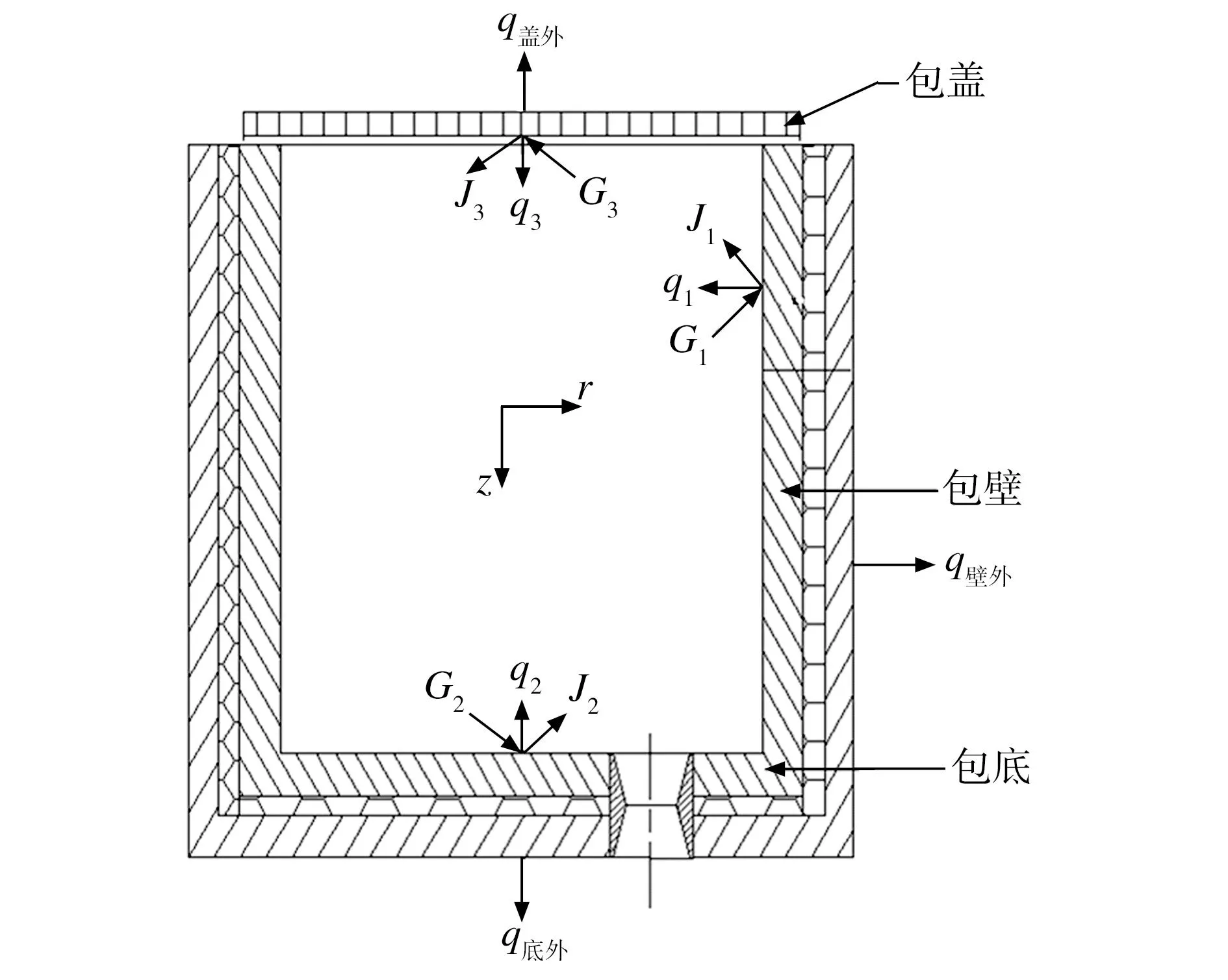
图2　空包阶段热流示意图

Fig.2 Schematic diagram of heat flux inside the empty ladle

(5)

(6)

其中，投射辐射密度

(7)

式(5)～式(7)中：εi为各内表面辐射率(黑度)；σ为玻尔兹曼常数，取5.67×10-8W/( m2·K4)；Ti,sur为各内表面温度，K；Fik为各内表面之间的辐射换热角系数。

每一表面的净热损失

(8)

式(5)～式(7)联立得到有效辐射的节点方程：

(9)

所有节点的有效辐射方程用矩阵形式可以表示为

(10)

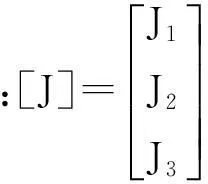
1.3钢水温度变化模型

1.3.1出钢过程钢水温降

钢水进入钢包内的温度变化表示为：

(11)

式中：M钢为钢包内钢水质量，kg；Cp钢为钢水比热容，J/(kg·K)；T钢为钢水温度，K；ρ钢为钢水密度，kg/m3；r进包为出钢钢流进包时的半径，m；v进包为出钢钢流进包速度，m/s；T进包为出钢钢流进包温度，K；A壁内、A底内为与钢水接触的包壁和包底面积，m2；q渣面为出钢阶段通过熔池自由表面的热流密度，W/m2；A渣面为出钢阶段熔池自由表面面积，m2；Qalloy为钢包装钢过程中向钢包加入脱氧剂、合金料等引起的热量变化，J。

出钢过程中钢水与包壁的接触面积是出钢时间的函数，为计算这个阶段包壁所通过的热流和相应的温度分布，将钢包内与钢水接触的包壁部分沿高度按出钢时间分成n个小垂直段，每个小垂直段对应包壁的一个圆柱面。出钢过程中，整个高度上的每一环可能处于不同的温度，相应包壁厚度方向的温度由每一垂直截面上中点温度来表示。

1.3.2传运过程钢水温降

在满包传运阶段，钢水通过包壁、包底和渣层向外传热，钢包内钢水温度的变化表示为：

(12)

式中：q渣内为通过与钢水接触的渣层内表面的热流密度，W/m2；A渣内为与钢水接触渣层内表面的面积，m2。计算渣层的温度分布时，渣层外表面与其上方钢包侧壁、环境之间构成一封闭辐射热交换空间，通过前述方法计算渣层外表面的热流密度。钢渣在热循环过程中存在相变现象，因而其热物理参数在不同的温度范围内是不同的，各物性参数随温度的变化可参考文献[3]。

1.3.3LF精炼过程钢水温度变化

根据体系能量平衡建立LF精炼过程钢水温度变化速率方程[4]：

(13)

式中：Qarc为进入熔池的电弧热量，J，其中LF炉电弧传热效率通过模型计算曲线与实测钢水升温曲线的对比校正得到；Qslag为加入渣料热效应，J；QAr为氩气带走热量，J；Qrd为吹氩形成钢液裸露面对外散热量，J，依据文献[5-6]所给实验式计算；Qsl为渣层外表面散热量，J；Qln为钢包内衬吸热量，J。

1.3.4RH精炼过程钢水温度变化

RH真空室内钢水温度变化可表示为[7-8]：

(14)

式中：M2为真空室内钢水质量，kg；T2为真空室内钢水温度，K；Qs为真空室内钢水表面的辐射热量，J；Qgas为真空室内炉气带走的热量，J；Qc=ΔHCOΔ[C]W2为真空室内钢水脱碳产生的化学热，J，其中ΔHCO为脱碳反应放热，J/kg，Δ[C]为RH处理前后钢水含碳量之差，%；qm、qn和qp分别为通过RH真空室壁、底部以及上升管和下降管的热流密度，W/m2；Am、An、Ap分别为RH真空室壁、底部、上升管及下降管的面积，m2。

钢包内钢水温度变化可表示为：

(15)

式中：M1为RH精炼时钢包内钢水质量，kg；T1为RH精炼时钢包内钢水温度，K。

RH真空室外部空间辐射换热条件十分复杂，钢包内渣层表面与其上方的真空室底部外表面、浸渍管外表面以及环境之间组成辐射换热空间，如图3所示。但此辐射换热空间中各表面间的辐射角系数无法通过查表得到，也不能通过直接积分的办法计算，因此很难得到作为边界条件的热流密度。本模型首先用FLUENT软件计算各个表面在某一温度下的有效辐射和投射辐射，得到6个关于角系数的方程；再利用角系数的性质得到其它30个关于角系数的方程，求解这36个方程所组成的线性方程组可以得到各表面间辐射换热的角系数，进而计算得到真空室底部和渣层外表面的轴向热流以及浸渍管外壁的径向热流，分别作为真空室底部外表面、浸渍管外表面和钢包渣层表面传热方程的边界条件。

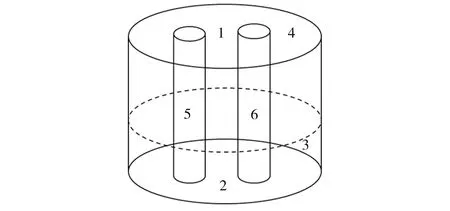
1—真空室底部外表面；2—钢包内渣层与空气接触表面；

Fig.3 Schematic diagram of radiant heat transfer outside the vacuum chamber

1.3.5喂线及浇注过程钢水温降

钢水在RH精炼后喂硅钙线阶段的温度变化可表示为：

q底内(τ)A底内+q壁内(τ)A壁内+q渣内(τ)A渣内]

(16)

式中：Qwire为喂线吸收的热量，J。

根据硅钙线的组成，将单质Ca、Si、Fe等元素的物理热和化学热折合成硅钙线的热效应后计算加入钢液的总热量，考虑了Ca的收得率。浇注过程中钢水温度的变化按出钢过程的逆过程计算。模型中边界换热系数采用文献[9]中的方法计算。

2模型的求解

首先进行钢包的网格划分，空间步长取为1 mm，由于钢包由多层材料组成，材料的热物性参数在两种材料的交界面上发生了阶跃式变化，故钢包的网格划分采用内节点法。

然后取时间步长Δt=1 s，根据划分的单元将包壁和包底的传热方程离散化。由于工艺过程时间较长，因此选用全隐式差分形式。全隐式差分是一种绝对稳定的差分格式，用现时刻一个节点的温度表示下一时刻相邻三个节点的温度。渣层和包盖为一维传热，其代数方组的系数是三对角阵，用求解速度最快的直接解法TDMA法(追赶法)求解。对于钢包传热代数方程组，其系数矩阵为五对角矩阵，无法直接用TDMA法求解，采用ADI法(交替方向隐式法)求解。钢包内的辐射网络方法构成的代数方程组采用松弛法求解。

每一阶段的求解包括初始化、边界条件处理以及温度场计算，其中后一阶段的初始温度为前一阶段的终点温度，最后依次对各阶段的温度分布进行求解。

3模型的验证及分析

采用本文模型对宝钢一炼钢厂32炉次出炉后至浇注阶段的钢水温度进行预报，并与实测温度进行了比较(共224点)。结果显示，模型计算值与实测值的平均误差为5.6 ℃，最小误差为0.1 ℃，其中误差在±8 ℃以内的占87.5%，表明用该模型来预报钢水温度基本可行。图4和图5所示为其中一个炉次的钢水温度和钢包内衬温度变化情况。

实际生产中，LF进站钢水温度波动范围较大，为了达到要求的出站钢水温度水平，深脱硫钢种的LF处理周期经常达到50 min以上，远远满足不了多炉连浇的要求。在保持LF基准操作条件不变的情况下，运用该模型分析了钢包热状态、出钢过程、传运时间等因素对LF终点钢水温度的影响。

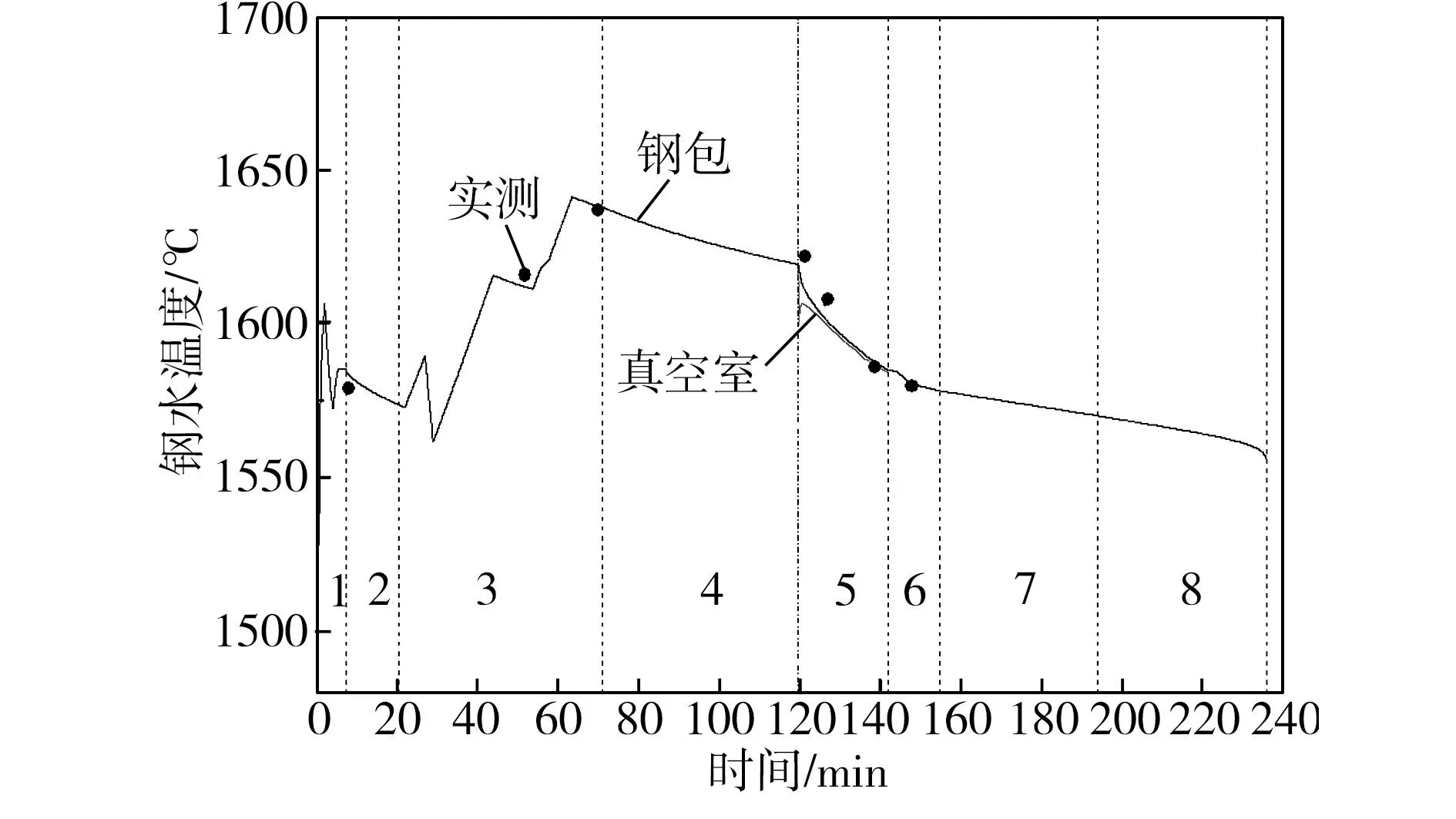
1—出钢；2、4、7—满包传运；

(a)钢包壁

Fig.5 Temperature distribution curves of the ladle lining at different stages

空包修理时间对钢水温降的影响比较明显，空包时间每延长30 min，LF终点钢水温度下降8～11 ℃。钢包烘烤10 min，LF精炼后钢水温度可提高2.9 ℃，但随着烘烤时间的延长，其对钢水温度的影响效果会降低，在保证一定烘烤时间的情况下，加快钢包周转、减少空包时间更为重要。

出钢量每减少20 t，出钢后的钢水温度会多下降6 ℃左右，即温度下降率约为0.3 ℃/t。而随着出钢时间的增加，钢水出钢温降速率减小，在所计算的出钢时间范围(3～11 min)内，出钢温降速率与出钢时间的关系为：

v=(9.890 59-0.027K)-(1.032 26-0.006K)t+(0.040 64-0.000 283K)t2

(17)

式中：v为出钢温降速率，℃/min；t为出钢时间，min；K=1726-T出钢，其中T出钢为出钢温度，℃。

出钢后传运时间对钢水温降的影响与钢水温度、钢包状态、渣层厚度等都有关。在目前的工艺条件下，出钢后10 min，钢水温降速度约为0.9 ℃/min；出钢后30 min，钢水温降速度约为0.45 ℃/min。出钢后渣层厚度约为60～70 mm，渣层散热对钢水温降的影响不大。

RH精炼过程中真空室内壁的吸热量较大，提高真空室内壁温度可以降低对LF出站钢水温度的要求，从而缩短LF处理时间。真空室内壁初始温度从900 ℃升至1400 ℃时，每增加50 ℃，LF终点温度可降低4.5 ℃左右，可缩短通电时间1 min以上。

4结语

本文根据LF-RH复合精炼生产超低硫钢工艺路径，考虑钢包热状态，基于冶金反应热力学、传热和热平衡原理建立了钢水温度预报模型。采用该模型预报了宝钢一炼钢厂32炉次超低硫钢从出钢至浇注过程中的钢水温度，计算值与实测值的平均误差为5.6 ℃，其中误差在±8 ℃以内的占87.5%。同时运用该模型分析了钢包热状态、出钢过程、传运时间等因素对LF终点钢水温度的影响，可为缩短LF精炼处理时间及开发高效精炼工艺提供参考。

参考文献

[1]殷瑞钰. 合理选择二次精炼技术, 推进高效率低成本“洁净钢平台”建设[J]. 炼钢, 2010, 26(2): 1-9.

[2]Rohsenow W M. 传热学基础手册[M].齐欣，译. 北京: 科学出版社, 1992: 375-377.

[3]Mikrovas A C, Argyropoulos S A, Sommerville I D. Heat transfer characteristics of molten slags[J]. Ironmaking and Steelmaking,1991,18(3):169-181.

[4]武拥军, 姜周华, 姜茂发, 等. LF炉精炼过程钢水温度预报模型[J].钢铁研究学报,2002,14(2):9-12.

[5]Peranandhanthan M, Mazumdar D. Modeling of slag eye area in argon stirred ladles[J]．ISIJ International, 2010, 50(11): 1622-1631．

[6]Castello-Branco M A S C, Schwerdtfeger K. Large-scale measurements of the physical characteristics of round vertical bubble plumes in liquids[J]．Metallurgical and Materials Transaction B, 1994, 25B(3): 359-371．

[7]刘浏, 杨强, 张春霞. RH精炼钢水温度预报模型[J].钢铁研究学报, 2000, 12(2): 15-20.

[8]韩传基, 刘青, 吴凯, 等. RH-MFB精炼过程中钢水温度预测模型[J].北京科技大学学报, 2006, 28(3): 248-252.

[9]Castillejos E A H, Acosta G F A, Betancourt S A, et al. On-line modeling for temperature control of ladles and steel during continuous thin slab casting[J]. Iron and Steelmaker, 1997, 24(7): 53-63.

[责任编辑尚晶]

Temperature prediction model of molten steel duringLF-RH process for ultra-low sulphur steel

FanZhiyong1，XiongWei1，HuHantao2，HuangYifei1

(1. Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education,Wuhan University of Science and Technology, Wuhan 430081, China; 2. Central Research Institute，Baosteel Group Corporation，Shanghai 201900，China)

Abstract:According to the process flow of LF-RH refining for ultra-low sulphur steel, a temperature prediction model of molten steel from tapping to teeming is developed based on metallurgical thermodynamics, heat transfer and thermal equilibrium principles as well as the thermal state of the ladle. It can provide temperature values of molten steel and temperature distribution in the ladle lining at any instant. The results of model verification show that, average error between the calculated and measured values is 5.6 ℃ and 87.5% of the error values are less than ±8 ℃. In addition, effects of ladle thermal state, tapping process, transport time and temperature of internal surface in RH vacuum chamber on molten steel temperature are analyzed by using this model, which are shown as reference for optimizing the refining process of ultra-low sulphur steel.

Key words：LF-RH refining; molten steel temperature; prediction model; ultra-low sulphur steel; thermal equilibrium; heat transfer

收稿日期：2015-12-28

基金项目：国家自然科学基金资助项目(51572203).

作者简介：樊智勇(1987-)，男，武汉科技大学硕士生.E-mail：452833101@qq.com通讯作者：熊玮(1975-)，男，武汉科技大学教授，博士.E-mail：xiongwei@wust.edu.cn

中图分类号：TF769

文献标志码：A

文章编号：1674-3644(2016)03-0170-05