基于Ansys Workbench的起重机吊臂结构全伸臂工况的有限元分析
李春风,董庆华,李少杰,郝清龙,王宇飞,曹 硕
(承德石油高等专科学校 工业技术中心,河北 承德 067000)
基于Ansys Workbench的起重机吊臂结构全伸臂工况的有限元分析
李春风,董庆华,李少杰,郝清龙,王宇飞,曹硕
(承德石油高等专科学校 工业技术中心,河北承德067000)
摘要:通过吊臂吊载,起重机能够实现大高度、大幅度的作业,吊臂是起重机的最主要承载构件之一,吊臂的分析研究对于起重机的结构优化起到了大的作用。以50 t起重机吊臂为例,借助软件Ansys Workbench对吊臂结构的全伸臂工况进行有限元分析,得到其变幅平面内各处位移和应力,为结构的改进和优化提供了一定的参考。
关键词:吊臂;Ansys Workbench;有限元
通过吊臂吊载,起重机能够实现大高度、大幅度的作业,吊臂是起重机的最主要承载构件之一,吊臂的强度对于起重机承载最大起重量时的整机起重性能起到了决定性的作用,吊臂自重对于起重机整机倾覆稳定性有着最直接的影响,吊臂结构的设计将直接影响整个起重机的性能,所以对吊臂进行有限元分析是很有必要的。
1吊臂工作原理、结构尺寸及其受力分析
1.1吊臂工作原理
起重机升降重物,是利用吊臂顶端的滑轮组支撑卷扬钢丝绳来悬挂重物,利用吊臂的长度和倾角的变化来改变工作半径和起升的高度,如图1所示。吊臂有两节、三节、四节、五节等不同形式,通过变幅机构来实现俯仰功能,如图2所示。起重臂顶端可以加滑轮,实现吊钩单倍率工作,提高工作速度。另外,起重臂顶端还可以同时加副臂,实现更大的起升高度。
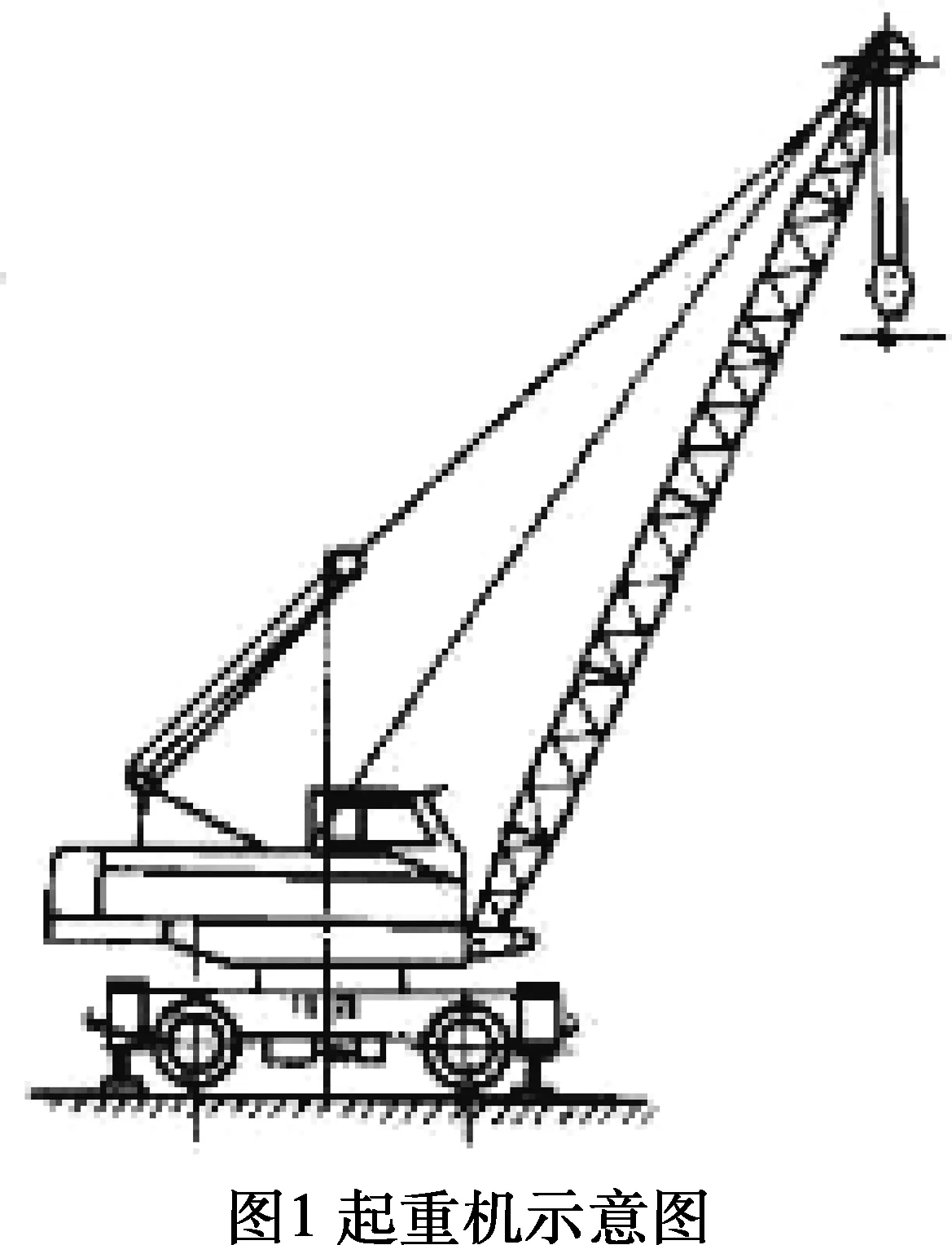
1.2吊臂结构尺寸
本文涉及到起重机基本参数为:回转速度:2 r/min,行走速度:70 km/h ,最大起重量50 t,最大起重力矩721.3 kNm,最大起升高度38.5 m,基本臂(第1节臂)举升高度为10.4 m;举升臂的总长为38 m,基本臂长10.2 m。举升臂为四节,结构见图3,四节的尺寸依次为:350×480、385×540、420×600、455×660(mm);起重举升臂的主体材料为合金结构钢,适当的选取16Mn进行加固,截面形状采用如图4 所示的“U”型截面。

1.3吊臂的受力分析
1)变幅平面内的载荷分析
起升绳拉力T:
(1)
式(1)中:φ1为吊臂动力系数;m为吊钩滑轮组的倍率;η为滑轮组效率;Q0为额定起重质量;G0为吊钩质量;g为重力加速度
将起升绳拉力T分解,平行于吊臂轴线方向的分力为T1=Tcosβ,垂直于吊臂轴线方向的分力为T2=Tsinβ;将垂直载荷Q分解,垂直于吊臂轴线方向的分力为Q1=Qcosβ,平行于吊臂轴线方向的分力为R=Qsinβ。其中β为伸缩臂在变幅平面倾角,Q为由起升载荷以及吊臂重量引起的垂直载荷。
伸缩臂有两个支点,分别是臂根车架之间的铰接点以及吊臂与变幅油缸之间的铰接点,因此可把吊臂简化为简支外伸梁进行分析。MLY为垂直力Q和起升绳拉力T对吊臂轴线偏心引起的力矩如公式(2)所示:
MLY=Qge1sinβ-Te2cosβ
(2)
式(2)中:e1为臂端定滑轮与吊臂轴线的偏心距;e2为臂端导向滑轮与吊臂轴线的偏心距。
2)旋转平面内的载荷分析
在旋转平面内,伸缩臂可视为一个端部自由、根部固定的悬臂梁。与在变幅平面受力情况一样,其承受的轴向力为T=R+T1,R是当吊臂旁弯时不变方向的轴向力,T1是吊臂旁弯时变方向轴向力,其中R=QsinβT1=Tcosβ
在旋转平面,伸缩臂的侧向载荷为货物的偏摆载荷,侧向力SY如公式(3)所示:
SY=(Q0+G0)gtgα
(3)
其中α为旋转平面摆角。
没有安装副臂时,力矩MLX=0,此时侧向力SY中的货物偏摆载荷S作用于臂端定滑轮的轴心处,吊臂受到扭矩MN作用,如公式(4)所示:
MN=(Q0+G0)ge1tgα
(4)
带入实际工况数据,得到吊臂受力汇总见表1。
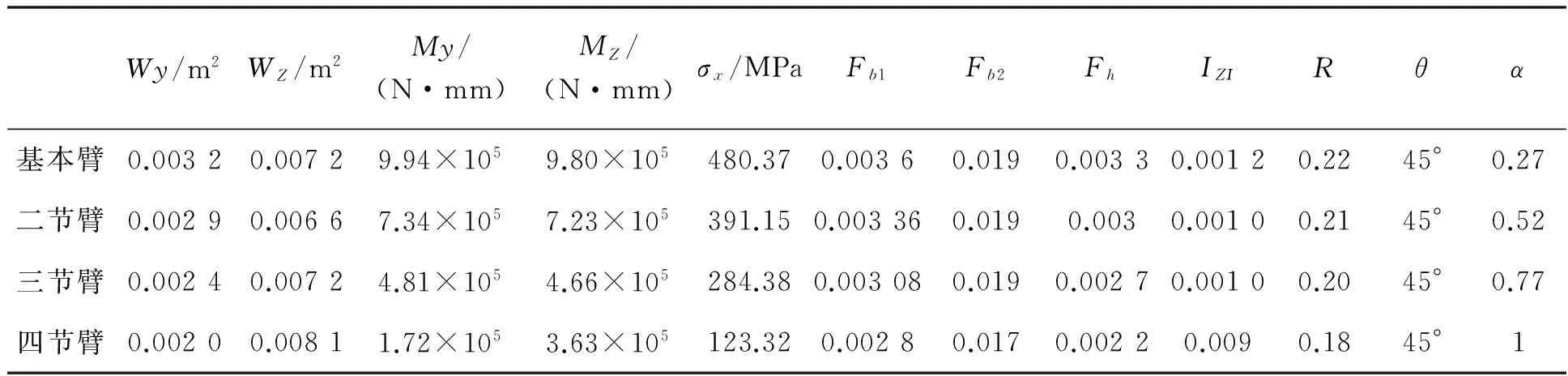
表1 吊臂受力汇总
2应用Ansys Workbench对吊臂结构进行有限元分析
2.1前处理
起重机吊臂由众多的机械零部件组成,可以看作是由杆件、板块、壳体、块体等或由它们组合组成的结构。ANSYS Workbench具有优秀的实体几何建模功能并提供了强大的网格划分工具,通过ANSYS Workbench软件,可以方便地构造出吊臂的几何模型和有限元模型,并对其进行准确的分析。
2.1.1建模
Design Modeler 是Ansys Workbench的建模平台,其用户界面与常用的三维CAD软件非常相似,主要功能集成于各项主菜单中[1]。DesignModeler不仅允许用户配置个人窗口来满足使用要求如利用鼠标就可以对窗口进行移动和调整,还提供了多项辅助工具如选择、拾取、组元、局部坐标系、工作平面等。利用DesignModeler进行建模不仅能够建立准确的几何模型而且能够大大减少建模时间。
建模时要考虑吊臂的重心位置和自身重量,必须以吊臂的真实工况进行建模,即先计算出吊臂的仰角θ(即吊臂的真实工况位置)的大小,再激活workplane,然后将workplane旋转θ角,在workplane内进行造型[3]。
吊臂既包括各节臂结构也包括伸缩系统各个传动件,结构比较复杂。若对整个吊臂进行完整建模的话,建模和分析会非常复杂,因此本文对吊臂结构进行了合理的简化。因为对于吊臂强度计算主要是分析吊臂危险截面处和各结构搭接处的局部应力分布,因此在进行有限元分析时可将吊臂前、后部结构进行简化,去除一些不必要的零件结构,使得整个吊臂只包含筒体和滑块结构,在保证相关设计参数和结构特征的情况下,不在模型中建立吊臂的伸缩机构[4]。 由于各节臂的筒体是由薄板构成的,因此建模时取中面尺寸进行造型,而基本臂的尾部及四节臂的头部结构复杂且刚性大,故建模时将其简化成了实体。利用ANSYS Workbench强大的造型功能,建立了吊臂简化结构的几何模型。
2.1.2各节臂与滑块间的连接简化
吊臂共有四节,各节臂相互之间可以滑动,每节之间有3个滑块,通过各节臂搭接处滑块的接触和挤压来实现力的传递。有两个思路,可以实现建模。思路1是建立接触单元,思路2是利用节点处的自由度耦合来实现,本文采用后者。添加约束使得吊臂和各个滑块之间保持接触,沿着接触面可以相对滑动,相应的节点(Coincident Node)间沿着接触面的法线方向自由度是耦合的,切线方向自由度是释放的。利用各节臂和相应的滑块在同一个节点位置的耦合,实现滑块和吊臂对应各个节点的耦合模拟。
2.1.3单元选取和网格划分
输入材料属性:查阅机械设计手册,选取相应的材料系数为:弹性模量E=2×105MPa,泊松比μ=0.3,密度ρ=7 850 kg/m3。根据材料系数定义相应的材料参数。
实体选用8节点的6面体单元Solid45,板采用Shell63板壳单元。Shell63为4节点的线弹性单元,遵循基尔霍夫假设,即变形前垂直中面的法线且变形后仍然与中面相垂直,且该单元能够同时考虑中面内的膜力以及弯曲变形,与吊臂的实际受载情况比较符合。
进行网格划分时,对吊臂的各个节臂筒体采用映射(mapped)和自由(free)的方式;滑块处为保证其形状为六面体,本文采用扫掠(sweep)的方式进行划分。整个网格的划分,为避免形状畸形,应保证控制单元形状尽可能规则。
由于每个节臂之间都有搭接部分,而且大部分节臂的板厚都不一样,不易选中,若是每块板逐个进行网格划分,不仅效率低下,计算繁琐,而且很容易出现错误,为此在建模前应先在实体模型上指定对应的属性,即将需要划分的单元、材料特性、实常数等赋予所有的实体,然后再对所有块、板等单元进行网格划分,最终得到吊臂所对应的有限元模型。
2.2边界条件
2.2.1施加载荷
吊臂所受的载荷包括侧载、吊重、钢丝绳在臂头的拉力;风载、液压缸的作用力以及伸缩机构钢丝绳的拉力。其中风载载荷作用在吊臂侧面上,而其它的载荷则需要加到各载荷相应位置的节点上或关键点上,为了使这些载荷加载点能成为节点,需在相应节点的位置处创建硬点(Hard points)。此外,由于钢丝绳在臂头的拉力及伸缩机构钢丝绳拉力的方向与整体坐标系方向不一致,为了便于加载荷,在建模时还需要旋转这些节的点坐标系。
2.2.2施加约束
在基本臂尾部与转台铰接处,变幅液压缸铰点处,对ROTY、ROTZ 2个方向的转动自由度和UX、UY、UZ 3个方向平移自由度进行约束,释放绕销轴中心回转的转动自由度ROTX。同时为保证臂的刚度和强度,设定应力Stressm和位移Deflm为状态变量,通过控制应力和位移来保证臂满足刚度和强度要求。
约束条件包括强度条件和刚度条件,强度条件为σ≤[σ],式中σ为危险点最大应力; [σ]为材料许用应力;刚度条件为DEFLM≤[f],式中DEFLM—变幅平面内最大位移;[f]—变幅平面内允许最大位移。
2.3后处理
Ansys Workbench的后处理中Geometry按钮控制云图的显示方法,共有四个可用选项:Exterior是默认的显示方式并且是常用的方式,IsoSurfaces对于显示相同的值域是非常有用的,Capped IsoSurfaces 是指删除了模型的一部分后的显示结果,删除的部分是可变的,高于或者低于某个指定值的部分被删除,Slice Planes允许用户去真实的去切模型。本文采用第一个选项。得到后处理云图结果:如图5所示的旋转平面位移图,如图6所示的变幅平面位移图。可见旋转平面最大挠度为672.62 mm,变幅平面最大挠度为780.31 mm,最大挠度均发生在吊臂最右端。得到图7所示变幅平面VON MISE应力图。可见变幅平面最大应力发生在图中红色区域,大小为[σ]max=541.5 MPa<[σ]H=885 MPa
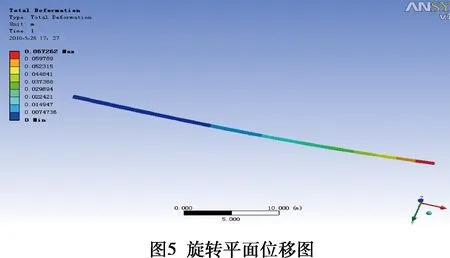


3结论
本文讨论了Ansys Workbench在起重机吊臂结构全伸臂工况的有限元分析中的应用。通过合理简化了吊臂结构,建立了起重机吊臂结构全伸臂工况的几何模型,然后根据材料的泊松比、弹性模量以及实际工况中承受的载荷等参数划分有限元网格,并根据吊臂运动和传力特点施加一定的边界条件,从而完成吊臂结构从几何建模、网格划分到施加边界条件的有限元建模过程,最终获得了旋转平面位移图,变幅平面位移图和变幅平面VON MISE应力图,其中创新之处在于利用节点耦合技术来模拟滑块和各节臂之间的连接,分析结果与经验相符,为结构的设计和优化提供了一定的参考。
参考文献:
[1]浦广益.Ansys Workbench基础教程与实例详解[M].北京:中国水利水电出版社,2010.
[2]李春风,董庆华,侯和龙.ANSYS软件在连杆有限元分析中的应用[J].承德石油高等专科学校学报,2015(2):20-23.
[3]杨晶,李卫民.汽车起重机吊臂的有限元分析[J].辽宁工学院学报,2007,27(3):195-198.
[4]郭耀松,张新忠.起重机吊臂结构的有限元分析[J].农业装备与车辆工程,2009(7):9-11.
Finite Element Analysis of Crane Boom Device in Full Arm Condition Based on ANSYS Workbench
LI Chun-feng, DONG Qing-hua, LI Shao-jie,HAO Qing-long, WANG Yu-fei, CAO Shuo
(Industrial Technology Center, Chengde Petroleum College, Chengde 067000, Hebei, China)
Abstract:As the main load bearing component of the crane, boom is used to elevate load, and to achieve great height and range operations. A research on boom plays an important role in bettering the structure of a crane. Taking the 50 ton crane boom for example, with the help of Ansys Workbench, finite element analysis of crane boom device in full arm condition is researched, and the displacement and stress in different positions in the variable amplitude plane is obtained, which will provide a reference for subsequent structure developing and optimization.
Key words:boom; Ansys Workbench; finite element
收稿日期:2015-10-28
作者简介:李春风(1981-),男,河北石家庄人,承德石油高等专科学校工业技术中心讲师,硕士,主要从事机械设计、有限元、可靠性等方面研究。
中图分类号:TH21
文献标识码:A
文章编号:1008-9446(2016)02-0017-05

