平方反比有心力场中粒子运动轨道的相对论修正*

舒新文　王竹平（安徽师范大学物理与电子信息学院，安徽芜湖241000）



平方反比有心力场中粒子运动轨道的相对论修正*

舒新文王竹平
（安徽师范大学物理与电子信息学院，安徽芜湖241000）

摘要：从相对论性粒子的拉格朗日函数出发，推导出相对性粒子在平方反比引力场中运动的轨道微分方程。该方程在低速运动情况下可过渡到经典力学的轨道方程，具有普遍意义，对于解决有心力和轨道关系的力学问题有一定的参考价值。

关键词：相对论；有心力；轨道方程

Abstract:Starting from the Lagrange function of relativistic particles，the paper deduces the orbital differential equation while the relativistic particles move in the inverse and square gravitational field.The equation can be transformed into the orbit equation of classical mechanics under the condition of low speed movement，which has significant reference valuefor solving the mechanics problem related tothere lationship between central force and orbit.

Keywords:theory of relativity；central force；orbital equation

在有心力场中，低速运动粒子的轨道微分方程可由毕耐公式描述。该公式在研究质点有心力作用下的运动轨道有重要地位和应用，如行星绕太阳的运动、微观粒子散射实验等。在平方反比力场中，由毕耐公式可以导出粒子的运动轨迹为圆锥曲线（椭圆、抛物线和双曲线），其具体形式由轨道方程的偏心率（或总能量）决定［1］。在高速运动情况下，粒子具有相对论性。目前对相对论性粒子在有心力场中运动的研究较少［2，3］。文章从构建相对论情况下的拉格朗日函数出发，利用拉格朗日方程建立了受平方反比有心力作用的相对论性粒子的运动轨道方程，得到了粒子的开普勒运动轨道的相对论修正。研究结果对解决有心力和运动轨道的普遍关系这一力学问题有一定的参考价值。

设相对论性粒子的惯性质量为m，现考虑粒子在质量为M所产生的引力场中运动，具有势能其中k=为相对性运动粒子到M的距离。此粒子的拉格朗日函数为［4］

其中qi为系统的广义坐标，可取｛qi｝=｛γ，θ｝。将（1）式代入（2）式，并利用极坐标下的速度表达式，可得粒子关于｛qi｝=｛γ，θ｝的运动微分方程分别为：

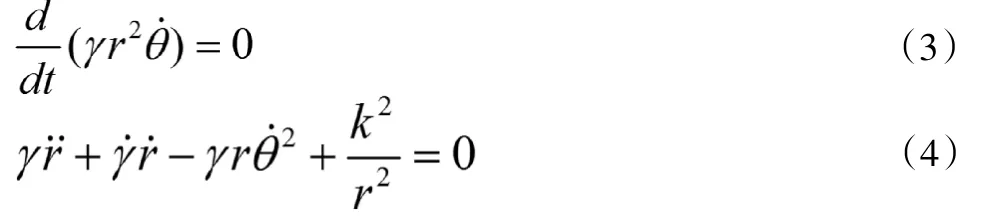
式（3）类似于低速情况下的运动初积分，动量矩守恒。因此，定义常数，可得

将（5）式和（6）式代入方程（4），得到粒子运动的轨道微分方程

（8）式即为相对论性粒子在平方反比有心力场中的轨道微分方程。式中为粒子开普勒运动轨道的相对论改正项，其值与运动速度有关。当v<

在实际物理问题中，由于λ是随运动速度（也即θ）变化而变化的物理量，（8）式为非线性二阶微分方程。一般来说，数学上不易直接求其通解，但可以通过数值计算的方法，进一步研究相对论粒子具体的运动轨迹特征，以及考察由于相对论性运动引起的轨道实际变化。这对处理相关力学问题具有一定的参考价值。

参考文献

［1］周衍柏.理论力学教［M］.北京：高等教育出版社（第三版），2009：65-74.

［2］于洛平.相对论性粒子在有心力场中的轨道微分方程［J］.山东师范大学学报（自然科学版），1993，8（2）：107-108.

［3］于洛平，官文栎.相对论性平面谐振子的轨道［J］.山东师范大学学报（自然科学版），1994，9（1）：31-35.

［4］徐永兴，朱珉仁.狭义相对论中自由质点拉格朗日函数的一种推导方法［J］.大学物理，1989，11（1）：49-50.

中图分类号：O41

文献标志码：A

文章编号：2096-000X（2016）12-0250-02

*基金项目：安徽省自然科学基金（编号：1608085QA06）资助。

作者简介：舒新文（1982-），男，安徽怀宁人，安徽师范大学副教授，博士，主要从事大学物理教学和天体物理研究工作。