改进的小波阈值图像降噪算法实现
甘航萍,王 力
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
改进的小波阈值图像降噪算法实现
甘航萍,王力
(贵州大学 大数据与信息工程学院,贵州 贵阳550025)
摘要针对图像降噪中的不连续性、存在恒定偏差等问题,在Dohono等提出的硬、软阈值法基础上,提出了一种改进的指数函数阈值降噪算法。与传统阈值降噪法相比,该方法不仅克服了传统方法的不足,且具有更好的灵活性。仿真实验结果表明,该改进阈值法的降噪效果无论在信噪比增益及均方误差上,或是在视觉效果上,均优于传统阈值降噪法。
关键词小波阈值降噪;信噪比;均方误差;图像复杂度
图像在获取过程中会受到各种噪声的干扰,这严重影响了图像处理和识别的效果,所以在图像信号预处理中,对含有噪声图像信号进行降噪处理就显得格外重要[1]。目前随着对小波的研究不断加深,运用小波分析已成为图像降噪处理中重要的方法之一。常用的小波降噪算法大致可分为模极大值法、相关性法和小波阈值法三类。其中,最常用的是由Donoho提出的阈值法,其简单易懂、计算量小,但各自存在一定的缺陷[2-3]。随后出现了诸多对传统方法的改进算法,如许丽群提出了软硬阈值折中法,结合了硬、软阈值法各自的特点,降噪效果也较传统有所提高,但提高的效果不明显[4]。王春丽提出采用加权的阈值函数作为改进的阈值法,但式中的调节因子和阈值的确定需要引入信息熵,过程比较复杂、繁琐[5]。邢国泉提出的改进法虽然阈值函数构造简单,计算量小,但降噪效果提高并不明显[6]。
为此,针对传统阈值法研究的不足,本文在文献[6]中的算法基础上提出了一种改进阈值函数,引用指数函数,构造思想简单。将叠加了高斯白噪声的图像信号在Matlab平台上进行降噪仿真实验,结果表明,在视觉效果和信噪比上均优于传统算法和文献[6]算法。
1阈值降噪原理
设有如下的图像信号
y(n)=x(n)+e(n),1≤n≤n
(1)
其中,y(n)为含有噪声的图像信号;x(n)为原始图像信号;e(n)是方差为σ2,服从N(0,σ2)的高斯白噪声。
小波阈值降噪就是根据信号和噪声的小波系数在不同尺度上具有不同性质的原理将信号与噪声区分,并去除噪声[7]。小波阈值降噪流程如图1所示。

图1 小波阈值降噪原理图
由此可见,阈值选取及阈值函数是小波阈值降噪过程中较为重要的因素。
1.1阈值选取
通常情况下,选取的阈值过小时不能彻底降噪,而选取过大时则可能滤掉有用的图像信号。因此,阈值选取是小波降噪的关键因素之一。常用的阈值选择估计有[8]:
(1)固定阈值表达式为
(2)
其中,T表示阈值;N为图像的像素点数;
(2)无偏似然阈值。给定一个阈值t,可得到其的似然估计,将非似然的t最小化便可得到所选的阈值;
(3)启发式阈值。该阈值综合前两种阈值,是最优预测变量阈值选择。在低信噪比情况下,采用固定阈值形式;在高信噪比情况下,利用启发式函数自动在前面两种阈值中选取较小者作为阈值;
(4)极值阈值。该阈值原理将最大风险最小化。选取的算法是
(3)
其中,N为图像的像素点数,4种阈值比较如图2所示,分别选取上述4种阈值对输入图像信噪比与降噪后图像信噪比改善量的关系进行比较。

图2 4种阈值比较图
如图2所示,选取固定阈值法时,从整体上看,图像降噪后的信噪比明显增加,综上所述,本文选用固定阈值估计。
1.2传统的阈值函数
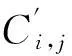
(1)硬阈值函数为
(4)
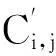
(2)软阈值函数为
(5)

2改进的指数函数阈值降噪法
除了传统的硬、软阈值函数,文献[6]中提出的小波阈值降噪函数为
(6)
文献[6]函数算法简洁,构造思想简单,但降噪效果不理想。
综上所述,为克服硬、软阈值降噪算法的缺点,本文在文献[6]算法的基础上提出一种基于改进指数函数的小波阈值降噪算法,如下
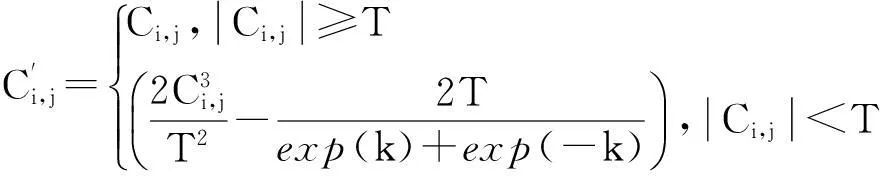
(7)
该函数的左极限
右极限
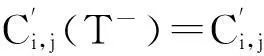
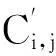
3仿真实验结果及分析
3.1仿真实验方案
本文在Matalab平台上完成上述改进阈值降噪法的仿真实验。经过反复的实验比较,选用Bior1.1小波对其进行分解,最大分解层数为2层,对于不同的分解尺度i,各阈值函数均采用相同的阈值T。本文采用了两种实验对比方案。
方案1对Lean图像加入了均值为0,方差为0.01的高斯噪声,分别用传统的硬阈值法、软阈值法、文献[6]和本文基于改进的指数阈值函数法进行图像降噪实验,比较图像降噪后的信噪比(SNR)和均方误差(MSE)。
方案2用硬阈值法、软阈值法和本文改进的方法分别对加入不同方差噪声,不同复杂度的Lean图像和Hyderabad图像进行图像降噪实验,比较图像降噪后的信噪比SNR。
3.2仿真结果分析
仿真实验结果主要比较两个性能指标,即降噪后图像的信噪比SNR和均方误差MSE。经小波降噪后图像的信噪比定义为
(8)
其中,x(n)为原始图像信号;x(n)′为经过小波阈值降噪后的图像信号。方案1实验获得的结果如图3所示。

图3 4种阈值降噪算法对图像降噪的结果比较图
如图3所示,用软阈值降噪法对含有高斯白噪声的图像进行降噪比用硬阈值法降噪效果好,但降噪后图像比较模糊。而文献[6]和本文改进的算法在视觉效果上优于传统的硬、软阈值降噪法,为进一步说明本文算法的优越性,将对Lena图像进行降噪实验获得的结果如表1所示。
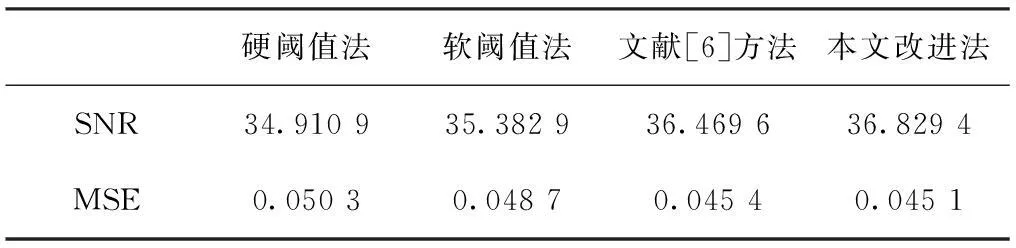
表1 4种降噪法对Lena图像降噪后的SNR和MSE
如表1所示,对比降噪后图像的信噪比和均方误差,本文改进的方法在降噪效果上明显优于传统阈值降噪法,略优于文献[6]的算法。方案2实验获得的结果,如图4所示。

图4 改进的阈值改进算法对两幅图像降噪
图4中,图4(b)和图4(e)为加入均值为0,方差为0.02的高斯噪声。从图中可看出,图4(d)比图4(a)复杂度高,因而对加入相同噪声的两幅图像进行降噪实验后发现,复杂度较高的图像的降噪效果远不如复杂度较低的图像。为更好地说明上述现象,实验获得具体的性能指标如表2所示。

表2 含不同噪声的两幅图像降噪后的SNR
表2可看出,对比图像降噪后的信噪比,本文改进的方法在降噪效果上优于传统阈值降噪法;随着加入噪声的增大,用不同的阈值降噪法降噪后图像的信噪比均有不同程度的降低;在其他条件都相同的情况下对比Lena图像和Hyderabad图像降噪后的信噪比,复杂度较低的Lena图像降噪效果明显优于复杂度较高的Hyderabad图像。
4结束语
文中在传统小波阈值降噪和文献[6]的基础上提出了一种基于改进指数函数阈值降噪算法。在图像降噪试验中,通过对比几种小波阈值降噪法,得到的结果显示:基于改进的指数函数阈值降噪法降噪效果最好,文献[6]的方法次之,传统的硬、软阈值法效果最差。随着噪声的增强,用不同的阈值降噪法得到的处理效果均有不同程度的变差。图像复杂度增大,用传统的阈值法和本文改进的方法得到的处理效果都变差。下一步研究重点是进一步提高图像的降噪效果,并将本文方法用于不同光照强度的图像的降噪处理中,力求提高本文阈值降噪法的应用范围。
参考文献
[1]邱刚,闽晓勇,雷玉勇,等.基于多尺度阈值技术的小波去噪[J].现代电子技术,2006,29(17):87-89.
[2]李万社,李鑫,牛桂欣.基于小波阈值去噪的改进方案[J].陕西学前师范学院学报,2014,30(5):117-122.
[3]崔华,宋国乡.基于小波阈值去噪方法的一种改进方案[J].现代电子技术,2005,28(1):8-10.
[4]许丽群.小波阈值去噪改进算法研究[J].电子测量技术,2010,33(8):43-45.
[5]王春丽.改进的小波阈值去噪算法及其实现[J].兰州交通大学学报,2011,30(6):55-58.
[6]邢国泉,叶华山,张玉霞,等.基于一种新的阈值函数的小波图像去噪方法[J].生物医学工程杂志,2013,30(4):743-747.
[7]陈晓曦,王延杰,刘恋.小波阈值去噪法的深入研究[J].激光与红外,2012,42(1):105-110.
[8]刘杨.基于小波变换的图像阈值去噪研究与实现[D].成都:成都理工大学,2011.
[9]张金榜,孙艺笑,王润典,等.改进的阈值函数去噪算法[J].电子科技,2014,27(2):17-20,24.
Improved Wavelet Threshold Image De-noising Algorithm
GAN Hangping,WANG Li
(College of Big Data and Information Engineering,Guizhou University,Guiyang 550025,China)
AbstractAn improved threshold de-noising exponential function is proposed on the basis of hard and soft threshold method put forward by Dohono to address the discontinuity and constant bias problems in image noise reduction.The threshold value method overcomes the deficiency of the traditional threshold method and offers good flexibility.Simulation results show that the improved threshold method of noise reduction is superior both in SNR gain and MSE and in visual effect to the traditional threshold noise reduction method.
Keywordswavelet threshold de-noising;SNR;MSE;image complexity
doi:10.16180/j.cnki.issn1007-7820.2016.05.033
收稿日期:2015-09-29
作者简介:甘航萍(1990—),女,硕士研究生。研究方向:图像处理,数据挖掘。王力(1971—),男,教授,硕士生导师。研究方向:模式识别,信号处理与机器学习。
中图分类号TP391.14;TN911.7
文献标识码A
文章编号1007-7820(2016)05-124-04

