并联微环谐振器耦合诱导透明传输特性研究
张 尚,吴 蓉,王 朝,许利沙
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
并联微环谐振器耦合诱导透明传输特性研究
张尚,吴蓉,王朝,许利沙
(兰州交通大学 电子与信息工程学院,甘肃 兰州730070)
摘要通过对并联微环谐振器传输特性进行研究分析,针对结构参数影响耦合诱导透明效应的问题。文中采用微环传输矩阵理论得出传输函数表达式,利用Matlab软件仿真了各参数变化对透明效应的影响。研究结果表明,耦合系数k的增大,传播损耗系数a的减小或两环间距L的增大,均会使透明效应减弱;微环半径R的增大,透明效应无明显的变化,但谐振波长发生改变。
关键词微环谐振器;诱导透明;传输矩阵
近年来,微环谐振器(Micro-Ring Resonator,MRR)由于成本低、结构紧凑、滤波性能优越、便于与电子元器件集成等优点已成为硅基集成光学领域的研究热点。利用MRR在光通信领域中可实现诸多具有重要功能的器件,如滤波器[1-2]、激光器[3]、光开关[4]、调制器[5-6]、分插复用器[7]等。
电磁诱导透明是一种光同物质相互作用的过程中产生的一种非线性效应,其通过一种量子干涉效应改变了材料的性质,使一束原本被这种材料吸收的光在材料性质被改变后变得不被吸收,即通过这种效应可使一个原本不透明的材料变得透明。耦合谐振腔诱导透明(Coupled Resonator Induced Transparency,CRIT)效应是一种类电磁诱导透明效应(EIT-like)[8-9]。产生这种效应时会发生强烈的反常色散,导致光在介质中的群速度改变,因此可利用其对光速进行控制,实现光的延时和缓存。同时,高灵敏度的传感器上也可用到这种器件,因此透明效应在量子信息的处理和光信息的存储方面具有重要的研究价值。目前,基于微环谐振器的CRIT效应已成为研究热点,然而对于并联微环谐振器耦合诱导透明效应传输特性的理论研究却鲜见报道[10-12]。本文通过微环谐振理论和传输矩阵理论建立了相应的数学模型,运用Matlab软件对影响CRIT效应的4种因素进行了模拟仿真,得出了不同因素对CRIT效应的影响。
1理论分析
并联双环双波导器件的散射矩阵模型如图1所示。直波导与环形波导在耦合区(a1~a4)内进行能量交换。环形波导(R1和R2)的作用是引起其中所传播光信号的相位变化,同时会导致其振幅衰减。直波导(L1和L2)的作用和环形波导的一致,两环之间通过这两段直波导进行能量交换。
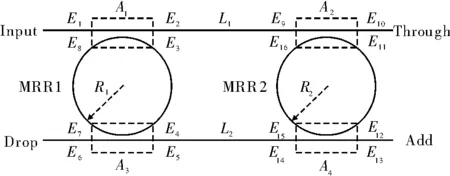
图1 并联微环谐振器散射矩阵模型
耦合区a1的散射矩阵关系可表示为
(1)
式中,k表示直波导和环形波导之间的耦合系数;t表示传输系数。选输入光信号的振幅E1=1,这样就相当于其它所有模式复振幅E均以其为基准进行归一化[13]。考虑耦合区是无损耗的,故传输因子t与耦合因子k满足t2+k2=1[13-14]。为便于计算,这里假设两环完全对称相同(即R1=R2=R,L1=L2=L),环波导和直波导的折射率均为neff。光信号在环形波导中传播的损耗系数由a描述(理想情况下微环无损耗时,a=1),而相位变化由θ描述。传播损耗系数a被认为与波长无关,而相位变化因子θ则是波长的函数,其关于波长的关系为
(2)
其中,β是两个环形波导内光信号的传播常数,β=2πneff/λ。光信号在波导中传播的有效折射率neff是波长的函数。两段直波导的长度均为L,传播损耗系数记作aL,相位变化因子记作θL。则相位变化因子与波长的关系表示为
(3)
因为两个微环之间可以通过直波导实现能量交换,所以它们之间存在耦合,故无法各自独立求解。若对整个器件建模求解,求解过程又复杂。为简化求解过程,可利用MRR的线性属性。即对于一个输入端和上载端均有光信号输入的MRR,可分别求解这两个输入光信号的输出结果,然后将其输出电信号在相应端口线性叠加,所得之和即为二者共同作用下的结果。
对于图1中的MRR1,其输入端与上载端的光信号分别为E1和E5。输入端光信号E1在其对应的直通端与下载端的贡献分别为
(4)
上式中,E21与E61分别表示电信号E1经过MRR1后在其对应的直通端(E2端)与下载端(E6端)所得到的电信号响应。
同理,上载端光信号E5在与其对应的直通端与下载端的贡献分别为
(5)
式(4)与式(5)分别是E1和E5独立作用下,E2端与E6端输出光信号的表达式。根据线性叠加原理,当二者共同作用时,E2与E6两个端口的输出光信号分别为
(6)
为了简便,将式(6)中的两个系数分别记为
(7)
式(7)中的T表示MRR1在直通端的传递函数,而D表示MRR1在下载端的传递函数。同理,对MRR2而言具有同样意义。
首先求解E2。E2可看作由两部分组成,第一部分来自E1经过MRR1时直通作用对E2产生的贡献,可表示为TE1,T的表达式如式(7)所示。第二部分来自于E2自身的反馈。具体过程是:首先E2经过L1传播得到E9;再经过MRR2下载得到E14;然后经过L2得到E5;最后E5经过MRR1的下载对E2产生贡献。这一过程所产生的贡献为
E22=[aLexp(jθL)]×[D]×[aLexp(jθL)]×[D]
(8)
式(8)中,4个中括号分别代表上述4个物理过程,E22表示E2自身对自身的贡献。综合E1和E2的共同作用,E2的表达式可写为
(9)
又由E1=1,根据式(9)即可求得E2
(10)
得到E2的表达式后,可得到器件直通端(Through端)的输出光信号E10的表达式
E10=E2aLexp(jθL)T
(11)
同理,下载端(Drop端)的输出光信号E6的表达式为
(12)
式(11)与式(12)即为器件两个输出端(Through端与Drop端)的输出光信号,其均为E2的函数。至此,端口Through与端口Drop的输出光信号均已表示为输入光信号E1的函数。
2传输特性分析
根据传输矩阵理论分析得出的表达式在Matlab软件上进行仿真,得到的结果如图2所示。实线和虚线分别表示在下载端(Drop)和直通端(Through)上得到的波形。从图中可看出,并联双环结构中在谐振点处发生了透射率的谱线分裂。在单环单波导结构中,器件处于谐振波长时在直通端会出现一个波谷,相应的在下载端会出现一个波峰。但在并联双环双波导结构中产生透明效应时,原来谐振波长处的波谷(波峰)处会分裂出一条狭窄的透明峰(谷)。这就是耦合谐振腔中的诱导透明现象。
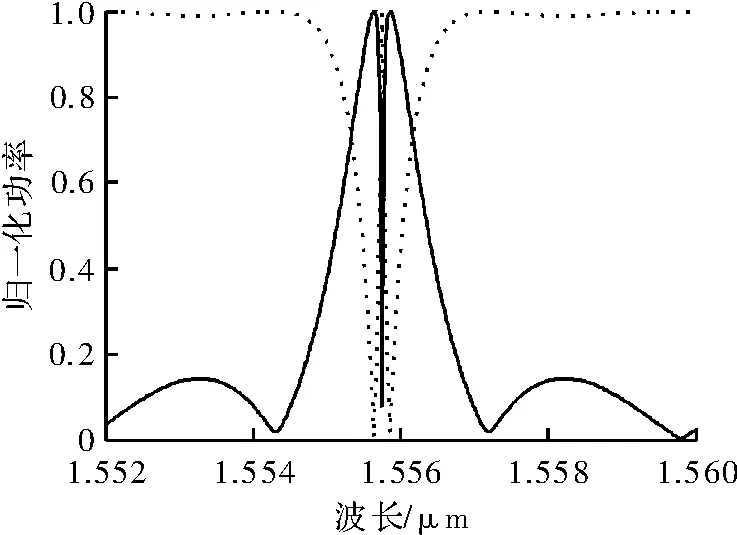
图2 并联微环谐振器产生透明现象时的传输特性谱
2.1环与波导之间耦合系数k对传输特性影响
图3为不同耦合系数k对CRIT的影响。分别取k的值为0.06,0.16,0.26和0.36。由图3可看出随着k的增大,谐振峰逐渐变宽,此时透明峰变得越来越窄,且越来越浅,说明k值得增大使得CRIT变弱。耦合系数k越大,谐振峰就变得越宽,器件的滤波性能就越差,因此k值不能取得太大。但k值也不能取得太小,k值越小,谐振峰越窄,隔离度越高,但对信号波长漂移的控制精度要求就越高。因此,应根据实际需求,选择合适的k值以获得理想的频谱特性。一般情况下k值在0.1~0.2范围内选取。

图3 耦合系数k对输出光谱的影响
2.2微环中传播损耗系数a对传输特性影响
图4为不同的传播损耗系数a对CRIT的影响。在理想情况下a=1。这里分别取a的值为1.0,0.99,0.9和0.8。由图4可看出随着a的减小,吸收曲线的整体谐振峰逐渐下降,且对a值的变化较为敏感,当a=0.99时,CRIT已有明显减弱;当a=0.9时,耦合谐振透明效应已经消失。所以a值越大越好,不过这应综合考虑材料、工艺和温度变化等原因对器件的影响。
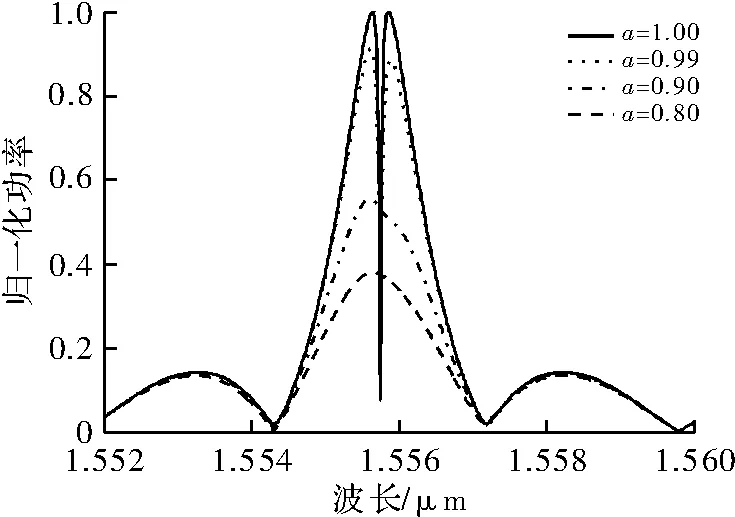
图4 环传播损耗系数a对输出光谱的影响
2.3环半径R对传输特性的影响
图5为不同环半径对CRIT的影响。由图5可看出随着微环半径R的增大,谐振峰的变化较小,透明效应减弱不明显,但透明谐振峰发生蓝移,这是由于随着半径的增大,光在微环里的光程增加,微环谐振条件发生改变而引起的。通过这一特性,可改变微环半径来控制透明峰的所对应的谐振频率,达到所需的透明频率或波长。

图5 环半径R对输出光谱的影响
2.4两环间距L对传输特性的影响
图6为两环之间间距L对CRIT的影响。由图6可看出随着两环间距L的逐渐增大,谐振峰逐渐变窄,透明峰也随之变窄,谐振波长两侧的波纹显著增多,这是由于光场在两个MRR之间多次反射形成的干涉条纹。这样虽然L的增大使得谐振峰变窄,但透明峰也变窄了,且波纹增多,这些均不利于透明效应的形成。因此,必须合理选择L的长度。
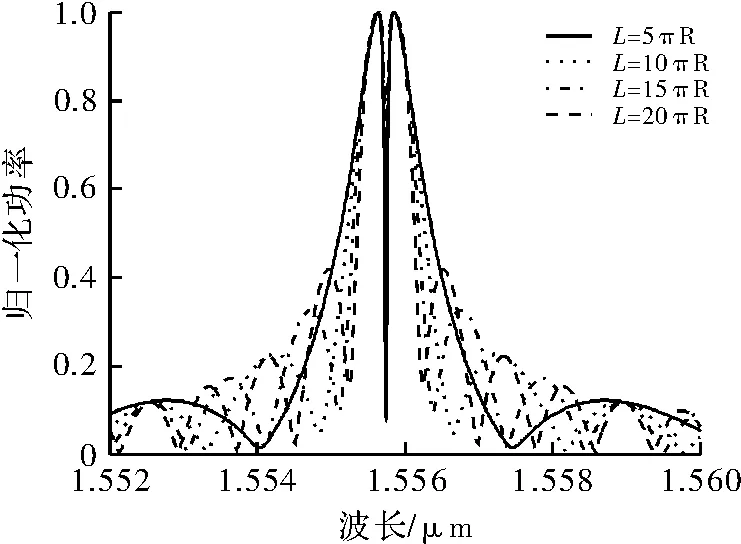
图6 环间距L对输出光谱的影响
3结束语
根据传输矩阵理论推导出并联微环谐振器产生透明现象的能量传输公式。根据线性叠加原理推导出并联谐振器直通端和下载端的能量传输方程。微环谐振器中每一个参数的改变,均对整个器件的性能造成了影响。耦合系数k增大,谐振峰就会变宽,器件的滤波性能就会变差,透明现象随之减弱。传播损耗系数a减小,吸收曲线的整体谐振峰逐渐下降且变得平缓,透明现象逐渐消失。微环半径R增大,透明谐振峰发生蓝移,谐振波长发生改变,透明现象没有明显变化。两环间距L的逐渐增大,谐振峰逐渐变窄,透明峰也随之变窄,谐振波长两侧的波纹显著增多,透明现象减弱。
对并联微环谐振器的一些基本结构参数对CRIT的性能和传输特性的影响进行了分析,为并联微环谐振器产生透明的设计提供了参考,提高了设计的灵活性,避免了器件设计和优化过程中的盲目性。
参考文献
[1]Little B E,Foresi J S,Steinmeyer G,et al.Ultra-compact Si-SiO2microring resonator optical channel dropping filters[J].Photonics Technology Letters,1998,10(4):549-551.
[2]杨建义,江晓清,王明华,等.采用单环微谐振器的光滤波器特性及其局限性[J].光电子·激光,2003,14(1):12-16.
[3]赵建宜,刘文,黄晓东,等.宽可调谐双微环耦合半导体激光器的模拟研究[J].光学学报,2012,32(2):178-182.
[4]刘毅,仝晓刚,于晋龙,等.基于热非线性效应的硅基串联双微环谐振腔全光开关[J].中国激光,2013,40(2):164-170.
[5]Hu Y,Xiao X,Xu H,et al.High-speed silicon modulator based on cascaded microring resonators[J].Optics Express,2012,20(14):15079-15085.
[6]曹彤彤,张利斌,费永浩,等.基于Add-drop型微环谐振腔的硅基高速电光调制器设计[J].物理学报,2013,62(19):260-265.
[7]Yan Hai,Feng Xue,Zhang Dengke,et al.Integrated optical add-drop multiplexer based on a compact parent-sub microring-resonator structure[J].Optics Communications,2013,289(4):53-59.
[8]Harris S E.Electromagnetically induced transparency[J].Physics Today,1997,50(7):36-42.
[9]Smith D D,Chang H,Fuller K A,et al.Coupled-resonator-induced transparency[J].Physical Review A,2004,69(6):063804(1-6).
[10]王永华,韦丽萍,臧俊斌,等.类电磁诱导透明效应在硅基微环谐振腔中的实现与优化[J].光子学报,2014,43(2):34-38.
[11]Fan Guofang,Li Yuan,Liu Xinhou,et al.Analysis about the effect of an on-chip all-optical analogue to electromagnetically induced transparency in the two resonators system[J].Infrared Physics & Technology,2012,55(2-3):173-176.
[12]Cui Danfeng,Xie Chengfeng,Liu Yaoying,et al.Experimental demonstration of induced-transparency based on a novel resonator system[J].Optics Communications,2014,324(4):296-300.
[13]Rabus D G.Integrated ring resonators[M].America:Springer Company,2007.
[14]Yariv A.Universal relations for coupling of optical power between microresonators and dielectric waveguides[J].Electronics Letters,2000,36(4):321-322.
Research on Coupled Resonator Induced Transparency TransmissionCharacteristics in Parallel Micro-Ring Resonators
ZHANG Shang,WU Rong,WANG Chao,XU Lisha
(School of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
AbstractThe transmission characteristics of parallel micro ring resonators are analyzed with emphasis on the structure parameters influencing the coupling induced transparency effect.In this paper,the transfer function expression is obtained by using the theory of the micro ring transmission matrix,and the influence of each parameter changes on the transparent effect is simulated using Matlab.The results show that the transparent effect weakens with greater coupling coefficient k,smaller propagation loss factor a or greater two ring spacing L.The increase in the Micro ring radius R does not lead to obvious change in transparent phenomenon,but the resonance wavelength changes.
Keywordsmicro-ring resonator;induced transparency;transmission matrix
doi:10.16180/j.cnki.issn1007-7820.2016.05.001
收稿日期:2015-11-07
基金项目:甘肃省自然科学基金资助项目(145RJZA133)
作者简介:张尚(1990—),男,硕士研究生。研究方向:光电器件。
中图分类号TN256
文献标识码A
文章编号1007-7820(2016)05-001-04

