微分形式障碍问题很弱解的正则性

程林娜,谷建涛（华北理工大学理学院,河北 唐山 063009）



微分形式障碍问题很弱解的正则性

程林娜,谷建涛
（华北理工大学理学院,河北 唐山 063009）

摘 要：本文首先给出微分形式障碍问题很弱解的定义，利用Hodge分解建立了微分形式的弱逆Hölder不等式，从而得到一类微分形式椭圆方程的障碍问题很弱解的正则性。

关键词：微分形式；障碍问题；正则性

1 引言

进年来，关于椭圆方程正则性的研究有许多重要的结果。对于微分形式的A-调和方程，已经建立起障碍问弱解的正则性［1-2］。本文利用Hodge分解建立了微分形式的弱逆Hölder不等式，得到微分形式的A-调和方程的障碍问题很弱解的正则性。

考虑如下微分形式的A-调和方程

本文主要结论如下。

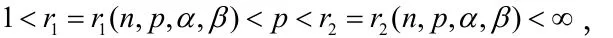
2 预备引理

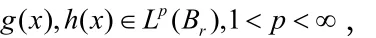
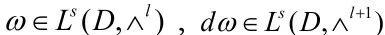
3 定理1.1的证明

结合（1.2）、（3.2）和（3.3），有

下面对（3.6）右端进行估计。首先结合（1.2）、Holder不等式、（1.5）、Young不等式和（3.4），可得

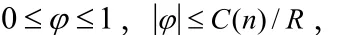
这里C=C（n,p,r,ε）。于是综合（3.6）-（3.9）可得

下面考虑上式右端最后一项。由于对u加减一个闭形式不影响方程的解，于是由引理2.2有

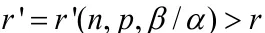
参考文献：

［1］高红亚,乔金静.微分形式障碍问题解的正则性［J］.河北大学学报,2011,31（05）：453-455.

［2］李松,谢素英.微分形式椭圆方程障碍问题解的局部正则性［J］.杭州电子科技大学学报,2013,33（04）：87-89.

［3］Giaquinta M. Multiple intgerals in the caculus of variations and nonlinear elliptic systems［M］. Princeton：Princeton U-niversity Press, 1983.

［4］B.Stroffolini. On weakly A-harmonic tensors［J］. Studia Mathematics, vol. 114, no.3, pp.359-366,2013.

基金支持：河北省自然科学基金（A2013209278）和华北理工大学自然科学基金（z201219）。

DOI：10.16640/j.cnki.37-1222/t.2016.12.196