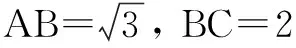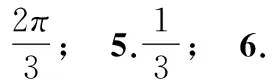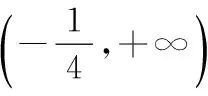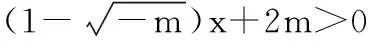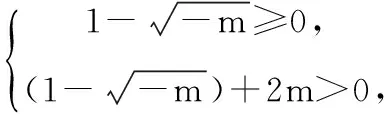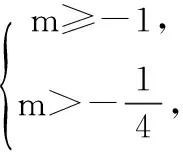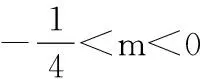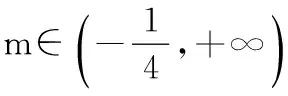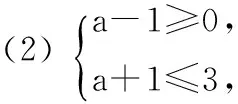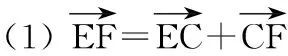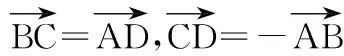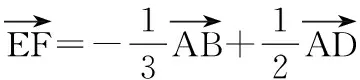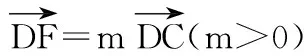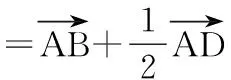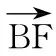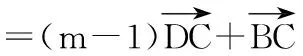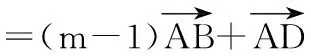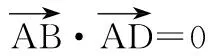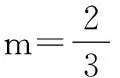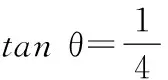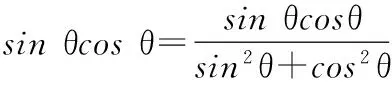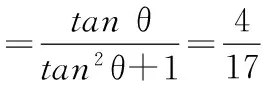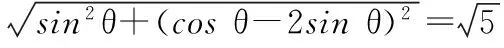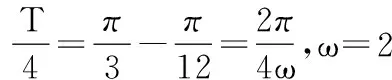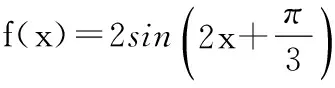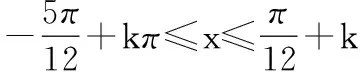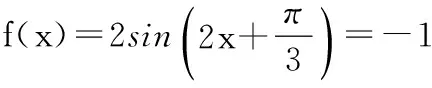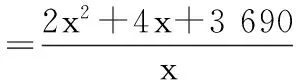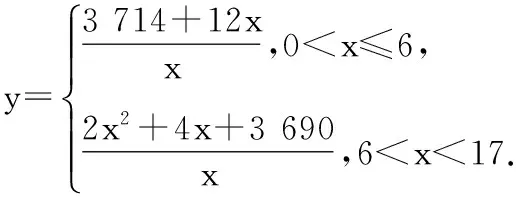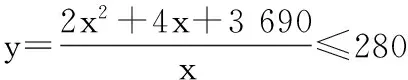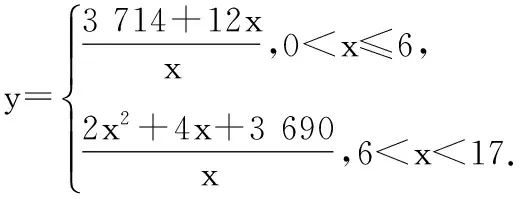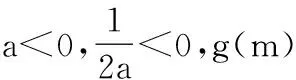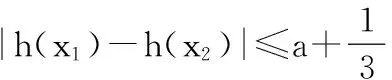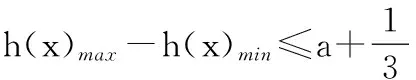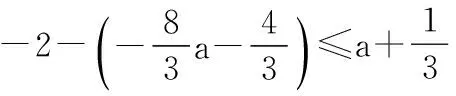高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合A={0,1},B={-1,1},则A∪B=______.

2.幂函数f(x)的图象过点(4,2),则f(2)=______.

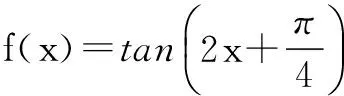
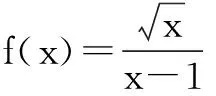
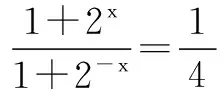
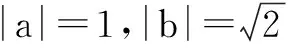
11.若关于x的方程cos2x-sinx+a=0在[0,π]内有解,则实数a的取值范围是______.

12.下列说法中,所有正确说法的序号是______.

① 终边落在y轴上的角的集合是

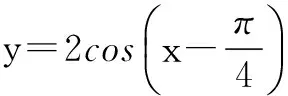
③ 函数y=tanx在第一象限是增函数;

13.若函数f(x)=loga(-x2+ax-1)(a>0且a≠1)有最大值,则实数a的取值范围是______.

二、解答题(本大题共6小题,共计90分.解答时应写出必要的文字说明、证明过程或演算步骤)

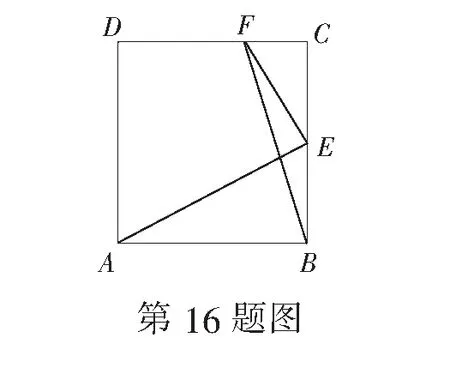
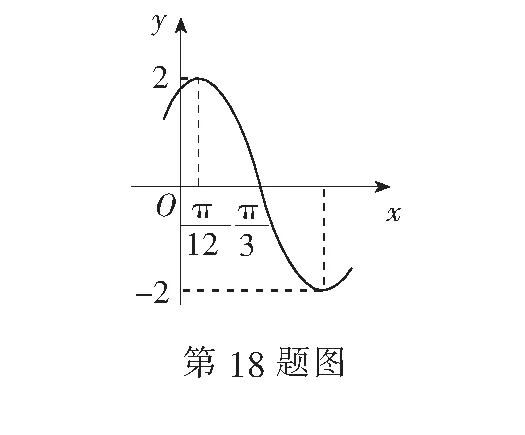
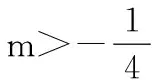
15.(本小题满分14分)已知集合A={x|a-1

(1) 若a=0,求A∩B;

(2) 若A⊆B,求实数a的取值范围.

16.(本小题满分14分)如图,在矩形ABCD中,点E是BC边上的中点,点F在边CD上.

17.(本小题满分15分)已知向量a=(sinθ,cosθ-2sinθ),b=(1,2),其中0<θ<π.

(1) 若a∥b,求sinθcosθ的值;

(2) 若|a|=|b|,求θ的值.

(1) 求A和ω的值;

(2) 求函数y=f(x)在[0,π]的单调增区间;

(3) 若函数g(x)=f(x)+1在区间(a,b)上恰有10个零点,求b-a的最大值.

(1) 求a,b的值.

(2) 一列由13辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为6米,其余汽车车身长为5米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第13辆汽车车尾离开隧道所用的时间为y秒.

① 将y表示为x的函数;

② 要使车队通过隧道的时间y不超过280秒,求汽车速度x的范围.

20.(本小题满分16分)已知f(ex)=ax2-x,a∈R.

(1) 求f(x)的解析式;

(2) 求x∈(0,1]时,f(x)的值域;

(3) 设a>0,若h(x)=[f(x)+1-a]·logxe对任意的x1,x2∈[e-3,e-1],总有

恒成立,求实数a的取值范围.

参考答案

一、填空题

11. [-1,1]; 12. ② ④; 13. (2,+∞);

第14题解题提示：

由题意知,f(x)为奇函数,且在R上单调递增,又对任意的x≥1有f(x+2m)+mf(x)>0恒成立.

若m≥0,∵x≥1,∴f(x)=x2≥1,∴f(x)>0,∴mf(x)≥0.

又∵x+2m>1,∴f(x+2m)>0,所以f(x+2m)+mf(x)>0,

故m≥0满足题意.

若m<0,则f(x+2m)>-mf(x),即

又f(x)在R上单调递增,

二、解答题

15.(1) 若a=0,则A={x|-1

A∩B={x|0

所以实数a的取值范围是1≤a≤2.

在矩形ABCD中,

=3(m-1)+2=1,

17.(1) ∵a∥b,

∴2sinθ=cosθ-2sinθ.

(2) ∵|a|=|b|,

∴cos2θ+sinθcosθ=0,

∴cosθ=0或sinθ=-cosθ.

18.(1) A=2,

又因为x∈[0,π],

函数f(x)在每个周期上有两个零点,所以共有5个周期,

19.(1) 当x=6时,

d=x+b=6+b=10,则b=4;

当x=16时,

则a=1,

所以a=1,b=4.

(2) ① 当0

当6

② 当0

当6

解得15≤x<123,所以15≤x<17.

答(1) a=1,b=4.

② 汽车速度x的范围为15≤x<17.

20.(1) 设ex=t,则x=lnt>0,所以

f(t)=a(lnt)2-lnt,

所以f(x)=a(lnx)2-lnx(x>0).

(2) 设lnx=m(m≤0),则

f(x)=g(m)=am2-m.

当a=0时,f(x)=g(m)=-m,g(m)的值域为[0,+∞).

当a≠0时,

f(x)=g(m)=am2-m

综上,当a≥0时,f(x)的值域为[0,+∞).

所以h(x)在[e-3,e-1]上满足

设lnx=s(s∈[-3,-1]),则

s∈[-3,-1].

当1-a<0即a>1时，r(s)在区间[-3,-1]单调递增,所以

当a=1时,r(s)=s-1,不符合题意.

当0

所以

7.求值:(lg5)2+lg2×lg50=______.