M-矩阵与其逆矩阵的q(A∘A-1)的进一步研究
周 平
(文山学院 数学学院,云南 文山 663000)
M-矩阵与其逆矩阵的q(A∘A-1)的进一步研究
周平
(文山学院 数学学院,云南 文山 663000)
摘要:利用特征值包含域定理,对M-矩阵A与其逆矩阵的τ(A∘A-1)作了进一步研究,并获得新的估计式;理论分析且数值算例表明,新估计式改进了Fiedler和Markham的猜想,同时也改进了有关的结果.
关键词:M-矩阵;最小特征值;下界;双随机
1符号说明和基本定义
定义1[1]设A=(ai j)∈Rn×n,若aij>0;i,j∈N,则称A为正矩阵,记为A>0;若aij≥0;i,j∈N,则称A为非负矩阵,记为A≥0.
定义2[1-10]设A=(ai j)∈Rn×n且ai j≤0;i≠j;i,j∈N,则称A为Z-矩阵,记所有n×n阶Z-矩阵所成之集为Zn.
定义3[2-3]若A=(ai j)∈Zn可表示为A=sI-P,其中P≥0,s≥ρ(P),则称A为M-矩阵.特别地,当s=ρ(P)时,称A为奇异M-矩阵;当s>ρ(P)时,称A为非奇异M-矩阵.记所有n阶非奇异M-矩阵所组成的集合为Mn.
定义4[4]设A=(ai j)∈Cm×n,B=(bi j)∈Cm×n,定义A∘B=(ai jbi j)∈Cm×n,即:
A∘B称为A和B的Hadamard积.
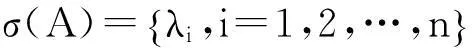
定义6[2]设A=(ai j)∈Zn,记q(A)=min{Re(λ):λ∈σ(A)},称q(A)为A的最小特征值.
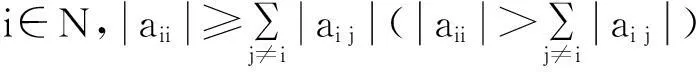
定义8[4]设A≥0且A的每一列元素和为1,则A称为随机的;若A≥0,A的每一列元素和为1且A的每一行元素和也为1,则A称为双随机矩阵.
2τ(A∘A-1)的新估计式

引理2[6-7]设A-1是双随机矩阵,则Ae=e,ATe=e,其中e=(1,1,…,1)T.
引理3[8]设A=(ai j)∈Rn×n,若A有如下不可约标准形:

其中P为置换矩阵,Ai或不可约或为0,i=1,2,…,s,则:
引理4[10]如果A=(ai j)为行严格对角占优M-矩阵,那么A-1=(βi j)存在,且有:

定理1设A=(ai j)∈Rn×n是非奇异M-矩阵,A-1=(βi j)是双随机矩阵,则:
证明当n=1时显然成立.下面对n≥2的情况进行证明.
情形Ⅰ 记λ=q(B∘A-1).当A为不可约矩阵时,根据已知条件和引理2有:

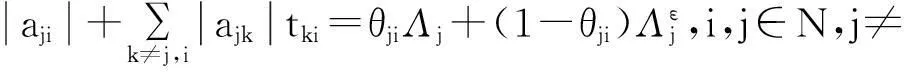
所以

即
故

情形Ⅱ当A是可约矩阵时,为了不失一般性,根据引理3,假设A具有如下块上三角形式:
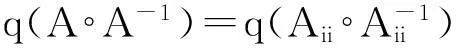
文献[10]中给出的定理3.3,说明文献[10]中的结果包含于定理1内.


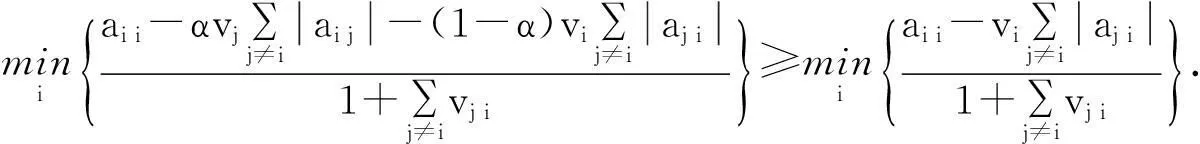

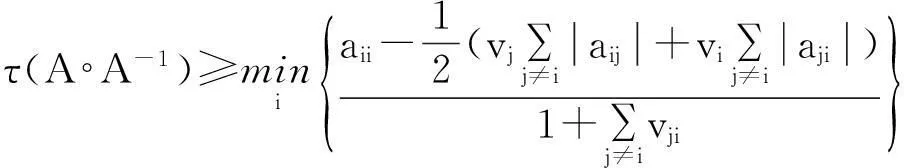
3数值例子

根据定义3知,A∈Mn,且既是严格行对角占优又是严格列对角占优矩阵.又应用引理2便知,A-1是双随机的.
应用Fiedler和Markham在文献[4]中的猜想,得q(A∘A-1)≥2n-1=0.2.
应用LiHou-biao等在文献[6]中给出的定理3.1,得q(A∘A-1)≥0.742 3.
应用ZhouDuan-mei等在文献[9]中给出的定理3.1,得q(A∘A-1)≥0.447 1.
应用ChenFu-bin在文献[10]中给出的定理3.3,得q(A∘A-1)≥0.897 6.
但应用本文定理1,当α=1/2时,得τ(A∘A-1)≥0.936 7.
事实上,应用Matlab7.1计算得q(A∘A-1)≥0.967 8.对比以上各估计式的计算结果,可以发现文中给出的对非奇异M-矩阵与其逆的q(A∘A-1)下界的估计式有效地改进了Fiedler和Markham的猜想以及一些现有的结果,提高了现有的估计精确度.
注2矩阵的特征值最主要是与矩阵的元素相关,但Fiedler和Markham的猜想给出的估计式仅与矩阵的阶数有关,文献[4,6,9,11,12,13]中给出的估计式,要么与M-矩阵的最小特征值相关,要么与Jacobi迭代矩阵的谱半径相关,当矩阵的阶数较大时,这些量都是难以计算的,从而应用它们估计q(A∘A-1)的下界是难以实现的,但文中定理给出的这些估计式仅与矩阵的元素有关系,计算简单易行.
参考文献:
[1]黄廷祝,杨传胜.特殊矩阵分析及应用[M].北京:科学出版社,2003:18-34.
[2]陈景良,陈向晖.特殊矩阵[M].北京:清华大学出版社,2000:123-257.
[3]BERMANA,PLEMMONSRJ.NonegativeMatricesintheMathematicesSciences[M].NewYork:AcedemicPress,1979:137-152.
[4]FIEDLERM,MARKHAMT.AninequalityfortheHadamardProductofanM-matrixandInverseM-matrix[J].LinearAlgebraanditsapplications,1988,101:1-8.
[5]LjiljanaCvetkovic.H-matrixtheoryandeigenvaluelocalization[J].NumerAlgor,2006,42:229-245.
[6]LIHB,HUANGTZ,SHENSQ,etal.LowerboundsfortheminimumeigenvalueofanM-matrixanditsinverse[J].LinearAlgebraanditsapplications,2007,420:235-247.
[7]LIYT,LIYY,WANGRW,etal.SomenewboundsoneigenvaluesoftheHadamardproductandtheFanproductofmatrices[J].LinearAlgebraanditsapplications,2010,432:536-545.
[8]李艳艳,李耀堂.矩阵Hadamard积和Fan积的特征值界的估计[J].云南大学学报(自然科学版),2010,32(2):125-129.
[9]ZHOUDM,CHENGL,WUGX.OnsomenewboundsforeigenvaluesoftheHadamardproductandtheFanproductofmatrices[J].LinearAlgebraandItsApplications,2013,438:1415-1426.
[10]CHEN F B.New inequalities for the Hadamard product of anM-matrix and its inverse[J].Journal of Inequalities and Applications,2015,35:1186-1195.
[11]高美平.M-矩阵与其逆矩阵的Hadamard积特征值的新下界[J].云南民族大学学报(自然科学版),2014,23(5):346-349.
[12]李艳艳,蒋建新.弱链对角占优M-矩阵最小特征值的下界研究[J].长江大学学报(自然科学版),2015,12(7):9-11.
[13]蒋建新,李艳艳.严格对角占优M-矩阵的逆矩阵无穷大范数的上界序列[J].湖北民族学院学报(自然科学版),2015,33(1):15-17.
责任编辑:时凌
Further Research on theq(A∘A-1) of anM-matrix and its Inverse
ZHOU Ping
(School of Mathematics,Wenshan University,Wenshan 663000,China)
Abstract:The q(A∘A-1)of an M-matrix and its inverse is further researched by using the theorem for localizations of matrix eigenvalues,and some new estimations are obtained.There are the theoretical analysis and numerical figure show that the new estimating formulas have improved the conjecture of Fiedle and Markham effectively and other existing results in some cases.
Key words:M-matrix;minimum eigenvalue;lower bound;doubly stochastic
收稿日期:2016-01-07.
基金项目:国家自然科学基金项目(11261049);云南省科技厅应用基础研究项目(2013FD052);文山学院“解析几何”精品课程项目.
作者简介:周平(1987- ),女,硕士,讲师,主要从事数值代数和矩阵理论及其应用.
文章编号:1008-8423(2016)01-0031-04
DOI:10.13501/j.cnki.42-1569/n.2016.03.008
中图分类号:O151.21
文献标志码:A

