广义协调COONS曲面厚薄板通用单元振动分析

陈　斌，张延庆

(北京工业大学建筑工程学院，北京　100124)



广义协调COONS曲面厚薄板通用单元振动分析

陈斌，张延庆

(北京工业大学建筑工程学院，北京100124)

摘要：厚薄板通用单元一直是板壳有限元研究中的重点和难点。根据单向厚板的基本方程推导得到内含剪切变形因子的插值基函数，基于Mindlin-Reissner厚板理论并结合广义协调思想，通过第2类有限元COONS曲面构造法及挠度和转角导数相关法构造出一个新的有效的厚薄板通用矩形单元，采用集中质量矩阵法得到单元的质量矩阵。通过编制MATLAB程序，采用子空间迭代法计算结构在不同板厚时的自振频率。将计算结果与理论解和大型通用有限元软件ABAQUS解进行比较，该单元具有良好的数值计算结果，能够实现动力学范围内薄板、中厚板以及厚板完全通用，具有工程应用价值。

关键词：结构力学；自振频率；厚薄板通用单元；COONS曲面；广义协调；MATLAB

对于结构计算而言，静力问题分析虽是首要的，但是往往动力作用引起的破坏才是致命的，这是引起结构严重破坏的主因。例如：地震作用引起的建筑物的坍塌；风振作用引起的高塔、桥梁的振动破坏；碰撞或者是爆炸对结构引起的冲击破坏等等。因此，在工程结构的研究、设计和安全性评估中，进行结构的振动特性分析是相当重要的，其中结构振动频率是非常重要和基础的动力特性。当前，板结构是建筑结构中最为常用也是最重要的结构形式，因此对板结构进行自由振动分析非常有必要。

由于板的特殊性，薄板与厚板的力学性能有所不同，对于薄板和厚板通常需分开单独计算，实际应用中对于薄板与厚板的划分无明显界限。为了提高计算效率和精度，人们开始探索厚薄板通用单元，而要实现厚薄板通用，则必须克服薄板情况下的剪切闭锁问题。此外，对于厚薄板壳的振动问题，采用常规的解析法求解是很困难的，而采用有限元法求解则能得到很好的效果[1-7]。有限元COONS曲面法作为有限单元法与计算几何学相结合的产物，构造单元简便高效，具有可以直接得到位移场函数显式的优点。

然而，到目前为止关于厚薄板通用的COONS曲面单元的振动分析研究尚少。文献[2—3]通过Timoshenko深梁理论推导剪切变形因子并从薄板理论出发构造出广义协调COONS曲面混合单元，能够实现动力下的中厚薄板通用。由于基于薄板理论构造，所以该单元缺乏转角位移场和剪切应变矩阵，对于厚跨比大的厚板(h/L>0.2时)，计算结果并不理想。因此，本文从Mindlin-Reissner厚板理论出发并结合广义协调思想，采用第2类COONS曲面构造法及挠度和转角导数相关法构造出一个新的厚薄板通用单元，通过编制MATLAB程序进行振动分析，为运用COONS曲面法研究板壳振动提供新的思路。

1单元构造

弹性厚板理论(Mindlin-Reissner厚板理论)[8-9]假设原来垂直板中面的直线在变形后仍保持为直线，但由于考虑了剪切变形的影响，其不再垂直于变形后的板中面。因此，采用此理论的板单元挠度位移w和转角位移θx，θy需各自独立插值。基于厚板理论来构造厚薄板通用单元，关键在于如何在薄板情况下克服剪切闭锁。为此，本文从单向厚板理论出发，推导出内含考虑剪切变形影响的剪切变形因子λ的插值基函数。构造单元时通过引入此插值基函数使板单元在薄板时的剪切刚度趋近于零，避免出现剪切闭锁。

1.1剪切变形因子

如图1所示，设单向厚板的挠度位移w为三次曲线，法线平均转角θS为二次函数，则有式(1)：

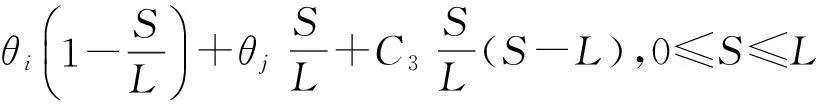
(1)

受Timoshenko深梁理论推导的启发，采用单向厚板理论推导得到[10-11]

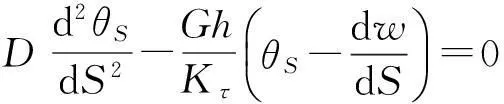
(2)

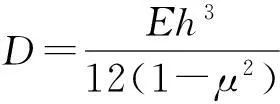
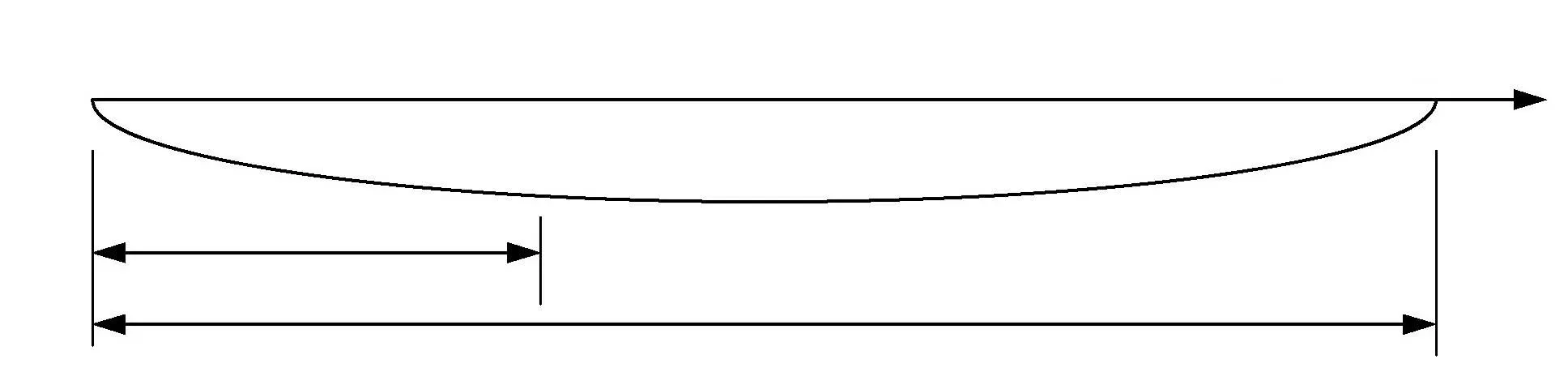
图1　单向厚板弯曲变形Fig.1　Bending deformation of one-way thick plate

将式(1)代入式(2)，积分得：

(3)

引入边界条件w|S=0=wi,w|S=L=wj得：

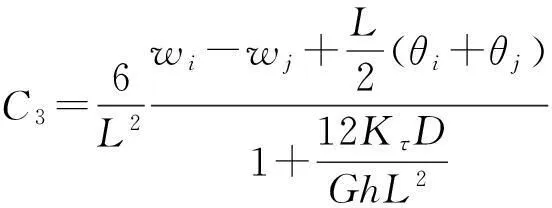
C4=wi。

(4)

设:

(5)

将式(4)和式(5)代入式(3)得单元挠度边界

w=F0(t)wi+F1(t)wj+G0(t)θi+G1(t)θj。

(6)

将式(6)代入式(1)，得单元转角边界

θS=f0(t)wi+f1(t)wj+g0(t)θi+g1(t)θj。

(7)

式(6)、式(7)分别为单向厚板的挠度位移函数和转角位移函数，均由物理方程推导得到。其中挠度位移插值基函数为

(8)

转角位移插值基函数为

(9)

通过以上公式可以看出，当板逐渐变薄时，即h/L→0时，λ→0，ρ→1时，

(10)

系数λ反映了剪切变形的影响，故称为剪切变形因子，它是薄板COONS曲面单元与厚板COONS曲面单元相互联系的桥梁。

综上所述，当h/L→0时，

θS→w′。

(11)

1.2单元挠度位移场

进行坐标系转换，无量纲自然坐标系(ξ,η)与总体坐标系(x,y)之间的关系为

ξ=x/a，η=y/b(0≤ξ,η≤1) ，

其中a和b为矩形单元的边长。

拟合单元4条边界的挠度位移场，并保证其在挠度和切向导数方向上保持协调：

[w(ξ,0)w(ξ,1)]=

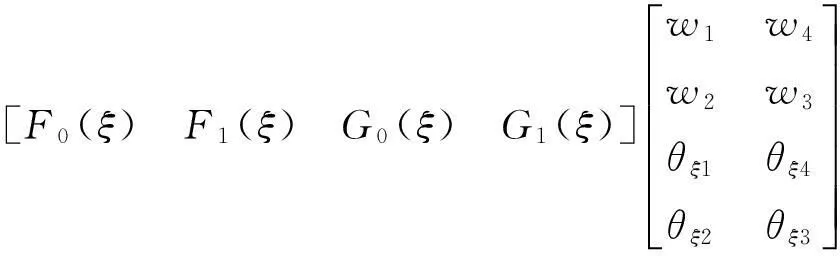
(12)

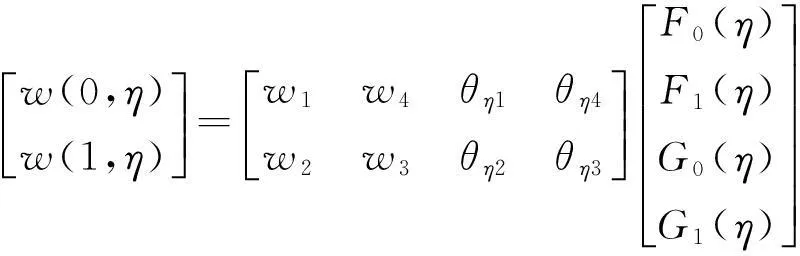
(13)

通过计算表明：以线性插值基函数为混合函数的ACM元的计算精度较高，但收敛速度较慢，而以第1类Hermite插值基函数为混合函数的Ferguson曲面元收敛速度较快，但计算精度较差，据此本文对于单元边界方向导数的拟合采用带有剪切变形因子的线性组合函数为插值基函数进行拟合，这样可以保证该单元在收敛速度和计算精度上有所提高。拟合结果如下：

[wη(ξ,0)wη(ξ,1)]=

(14)

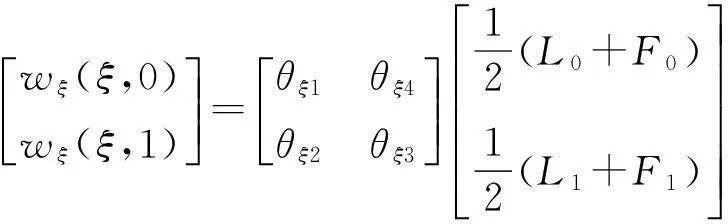
(15)

其中L0=1-t，L1=t，t=ξ,η。

再引入广义协调条件，使COONS曲面片边界处的法线导数满足广义协调，即令

(16)

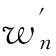
[Nw]=

[F0F00.5b(L0+F0)G0-0.5aG0(L0+F0)

F1F00.5b(L1+F1)G0-0.5aG1(L0+F0)

F1F10.5b(L1+F1)G1-0.5aG1(L1+F1)

F0F10.5b(L0+F0)G1-0.5aG0(L1+F1)]，

{δ}=[w1θx1θy1w2θx2θy2

w3θx3θy3w4θx4θy4]T。

[w]=[Nw]{δ}。

(17)

[Nw]的各项乘积因式中，前者是ξ的函数，后者是η的函数，前后顺序不可交换(下同)。

1.3单元转角位移场

为避免剪切闭锁，必须使厚板元的挠度位移场和转角位移场在h/L→0时满足导数关系，即满足Kirchhoff薄板理论的直法线假设。式(10)和式(11)已指出，当h/L→0时，挠度位移场w和转角位移场θx，θy满足导数关系。而h/L不趋于零时，挠度场和转角场并不满足导数关系，符合厚板理论的要求。因此，采用挠度位移场的“偏导数”作为转角位移场，但求导时附加约束性求导条件[12]，

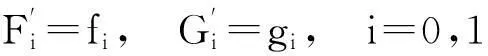
由此，就能得到厚薄板通用单元的转角位移场函数：

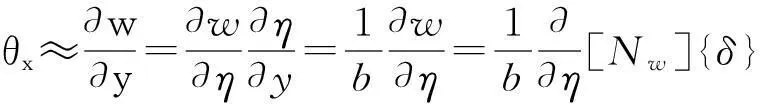
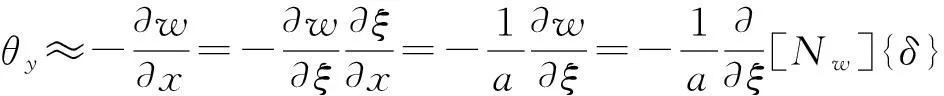
具体表达式分别如式(18)和式(19)所示。

(18)

(19)

1.4单元刚度矩阵

应变有5个分量，即

{χ}=[χxχy2χxy…γxγy]T=

单元刚度矩阵：

[k]e=[kb]e+[kS]e。

[kb]e=∫A[Bb]T[Db][Bb]dA为单元弯曲刚度矩阵，[kS]e=∫A[BS]T[DS][BS]dA为单元剪切刚度矩阵。

显然，当h/L→0时，[BS]→[0]，[kS]e→[0]，故不会出现剪切闭锁。

1.5单元质量矩阵

采用集中质量矩阵：

其中ne为单元节点数，ρ为材料密度。

1.6编程求解

基于MATLAB[13]强大的矩阵运算能力，本文采用MATLAB编制了结构计算程序，并采用子空间迭代法求解结构的自振频率。计算中只需修改板厚，即可实现厚薄板的自振分析，无须像ABAQUS分析时需根据厚跨比选用不同的单元进行计算。

2数值算例

数值算例描述：四边简支各向同性矩形弹性方板，边长为10 m，材料密度ρ=2 400 kg/m3，弹性模量E=3.0×1010N/m2，泊松比v=1/6。采用MATLAB编制的程序，按12×12划分单元，求解不同厚跨比(h/L)下前5阶频率值，并与理论解和ABAQUS解[14]进行对照，结果如表1和图2—图6所示。

图2　不同厚跨比一阶频率比较Fig.2　Comparison of the first order frequency 　　　by different thickness span ratio

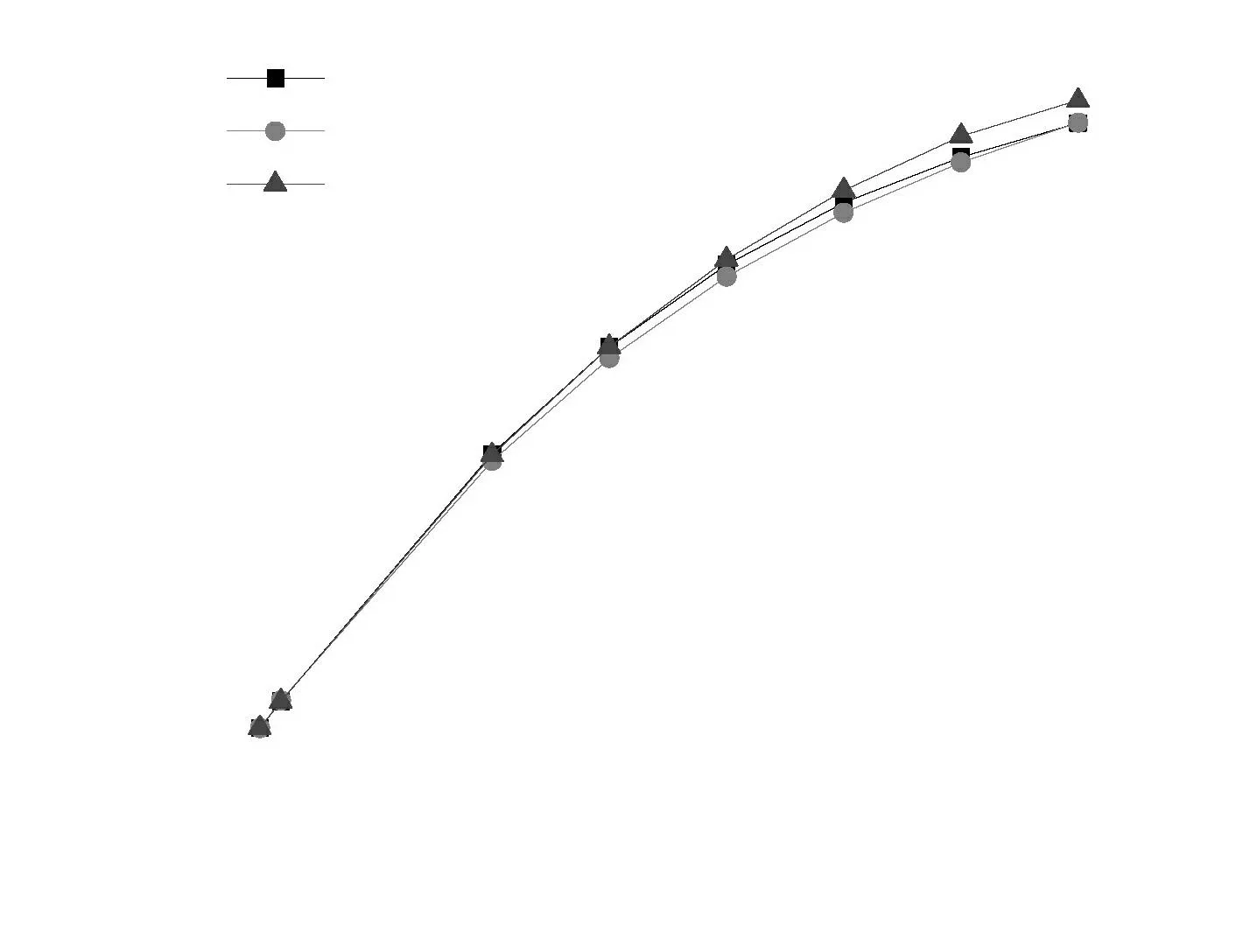
图3　不同厚跨比二阶频率比较Fig.3　Comparison of the second order frequency　　　by different thickness span ratio

阶次频率/Hz薄板h/L=0.001薄板h/L=0.01中厚板h/L=0.1中厚板h/L=0.15中厚板h/L=0.2中厚板h/L=0.25厚板h/L=0.3厚板h/L=0.35本文解0.32493.247430.70143.75655.35065.61074.66182.626(1,1)理论解0.32523.252031.44845.56557.96368.64077.59785.192ABAQUS解0.32713.268330.03742.71053.76763.33371.60278.763本文解0.81158.110075.116104.530128.290147.120161.930171.560(1,2)理论解0.81308.130175.451104.520126.860143.750156.180165.440ABAQUS解0.83348.326173.473101.450123.620141.030154.720165.540本文解1.295012.9370114.83154.520184.160206.180222.620234.980(2,2)理论解1.300813.0080116.04155.350182.970201.740214.800223.770ABAQUS解1.330912.2890111.590149.320177.230198.060204.070207.700本文解1.622216.2020143.500191.480225.190248.610265.040273.790(1,3)理论解1.626116.260141.320185.910215.390234.720247.550256.970ABAQUS解1.738517.353140.200186.430207.980210.850229.580231.740本文解2.100620.968177.750230.750266.200290.070306.490318.080(2,3)理论解2.114821.147177.620227.780259.350278.790291.450300.110ABAQUS解2.220122.150173.260208.730219.160245.850265.140278.400

注：表1中薄板的理论解参考文献[15]，中厚板及厚板的理论解参考文献[10]；ABAQUS模拟计算中，薄板采用S4R5单元，中厚板和厚板采用S8R单元。

图4　不同厚跨比三阶频率比较Fig.4　Comparison of the three order frequency 　　　by different thickness span ratio

图5　不同厚跨比四阶频率比较Fig.5　Comparison of the four order frequency　　　by different thickness span ratio

图6　不同厚跨比五阶频率比较Fig.6　Comparison of the five order frequency　　　by different thickness span ratio

由以上表1和图2—图6可以看出：本单元在不同厚跨比下的前3阶数值解基本与理论解吻合。随着阶数和板厚的增加，本文解的精度仍优于ABAQUS解，能够满足工程计算需要。本单元能够在动力学范围内实现薄板-中厚板-厚板的完全通用，能够得到收敛速度快、计算精度较高的数值结果。

随板厚和阶数增加而出现的误差与单元推导及程序编制时未考虑转动惯量和挤压变形的影响有关系。但相比于剪切变形的影响，以上的影响很小。为了提高精度，以后可在这方面进行相关研究。

3结论

基于Mindlin-Reissner厚板理论并结合广义协调思想，采用第2类COONS曲面构造法及挠度和转角导数相关法构造出一个新的厚薄板通用单元，通过自编MATLAB程序进行振动分析，数值算例表明该单元具有良好的收敛性和计算精度，能够实现动力学范围内薄板、中厚板及厚板的完全通用，具有工程实用性。

1)选用单向厚板基本方程推导出剪切变形因子，基于厚板理论构造出的COONS曲面单元能够实现动力下的完全厚薄板通用，可作进一步的研究和推广，以丰富大型有限元分析软件的单元库。

2)相比于第1类COONS曲面，第2类COONS曲面较复杂，自由度数也会增加，但收敛速度更快，计算精度更高。本文采用第2类COONS曲面构造法，通过引入广义协调条件消去自由度，从而得到消去节点扭矢的12参数矩形元，同时在单元边界法向导数拟合中使用内含剪切变形因子的线性组合函数作为插值基函数。数值算例结果表明，本单元具有良好的数值计算结果。

3)COONS曲面单元具有直接给出位移场显式的优点，已在静力问题分析中取得了较好的收敛性和精度，然而在动力问题分析中缺少研究。本文通过编制的MATLAB程序，对推导出的基于厚板理论的厚薄板通用的COONS曲面单元进行振动特性分析。计算表明，COONS曲面单元在动力问题分析中同样能够实现厚薄板通用，且具有良好的数值计算结果，为运用有限元COONS曲面法进行板壳的振动分析提供了借鉴。

参考文献/References：

[1]张延庆.板壳有限元计算几何理论[D]. 徐州:中国矿业大学, 1990.

ZHANG Yanqing. Computational Geometric Theory of Finite Element of Plate and Shell[D]. Xuzhou: China University of Mining and Technology，1990.

[2]张延庆，龙驭球. 厚薄板通用的广义协调单元COONS曲面构造法[J]. 工程力学, 1994, 11(2)：59-64.

ZHANG Yanqing, LONG Yuqiu. Formulation of a generalized conforming element for moderate thick plate based on COONS’ surface[J]. Engineering Mechanics，1994，11(2)：59-64.

[3]陈叶妮，张延庆. 用广义协调COONS混合曲面元分析中厚板的振动[J]. 工业建筑, 2006(sup1)：612-614.

CHEN Yeni，ZHANG Yanqing. Vibration analysis of moderate thick plate by generalized conforming element and COONS surface approach[J]. Industrial Construction，2006(sup1)：612-614.

[4]曹金凤，姜耀东，赵国景，等. 广义协调厚薄板通用单元TMT的固有振动分析[J]. 中国矿业大学学报，2007, 36(1)：91-96.

CAO Jinfeng，JIANG Yaodong，ZHAO Guojing，et al. Free vibration analysis of plate using a generalized conforming thick/thin element TMT[J]. Journal of China University of Mining and Technology，2007, 36(1)：91-96.

[5]曹金凤，姜耀东，韩志茹，等. 广义协调厚薄板通用单元的固有振动分析[J]. 力学与实践，2007，29(3)：30-35.

CAO Jinfeng，JIANG Yaodong，HAN Zhiru，et al. Free vibration analysis for plates using a generalized conforming thick/thin triangular element[J]. Journal of Mechanics in Engineering，2007, 29(3)：30-35.

[6]韩志茹，姜耀东，王丽，等. 广义协调厚薄通用板单元的动力特性分析[J]. 力学与实践，2009, 31(3)：69-72.

HAN Zhiru，JIANG Yaodong，WANG Li，et al. The dynamic property of generalized conforming thick/thin plate elements[J]. Journal of Mechanics in Engineering，2009, 31(3)：69-72.

[7]黄修长，钱振华，李俊，等. 应用基于解析式函数的广义协调四边形厚板元分析中厚板的自由振动[J]. 工程力学，2011, 28(9)：39-43.

HUANG Xiuchang，QIAN Zhenhua，LI Jun，et al. Vibration analysis of moderate thick plate by generalized conforming quadrilateral thick plate element based on analytical trial functions[J]. Engineering Mechanics，2011, 28(9)：39-43.

[8]MINDLIN R D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates[J]. ASME Journal of Applied Mechanics，1951, 18(1)：31-38.

[9]REISSNER E. On bending of elastic plates[J]. Quarterly of Applied Mathematics，1947, 5(1)：55-68.

[10]曹志远，杨昇田. 厚板动力学理论及其应用[M]. 北京:科学出版社，1983：57-124.

[11]郑照北，王宏凯. 板壳有限元COONS曲面法[M]. 徐州:中国矿业大学出版社，1993：52-73.

[12]王宏凯，郑照北. 一个有效的厚薄板通用COONS曲面矩形元[J]. 工程力学，1992, 9(1)：134-140.

WANG Hongkai，ZHENG Zhaobei. An efficacious COONS’ surface method for formulation of current finite element of thick and thin plates[J]. Engineering Mechanics，1992, 9(1)：134-140.

[13]刘卫国. MATLAB程序设计教程[M].第2版. 北京：中国水利水电出版社，2010.

[14]庄茁，曲小川，廖剑晖, 等. 基于ABAQUS的有限元分析和应用[M]. 北京：清华大学出版社，2009.

[15]曹志远. 板壳振动理论[M]. 北京: 中国铁道出版社, 1989：32-54.

Vibration analysis of generalized conforming and COONS’surface thick/thin plate element

CHEN Bin, ZHANG Yanqing

(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

Abstract:Thick/thin plate element has been the focus and difficulty in the study of shell finite element. According to the basic equation of one-way thick plate, the base function of interpolation containing the shear deformation factor is derived. Based on the Mindlin-Reissner thick plate theory and the idea of generalized coordination, the second kind of finite element COONS’ surface construction method and the derivative correlation method of deflection displacement and angular rotation displacement are used to derive a new effective thick/thin general rectangular plate element, then the lumped mass matrix method is used to get the mass matrix of the element. By using MATLAB programming, the natural frequencies of the plates with different thickness are acquired by a sub-space iteration method. Compared with the theoretical solution and the numerical value of ABAQUS, it is concluded that this element has good numerical calculation results, which can realize entirely common use for thin plate, cut deal and thick plate in dynamic range, and it has engineering application value.

Keywords:structural mechanics; natural frequency; thick/thin plate element; COONS’ surface; generalized conforming; MATLAB

文章编号：1008-1534(2016)03-0224-06

收稿日期：2016-04-04;修回日期：2016-04-24；责任编辑：冯民

作者简介：陈斌(1990—)，男，浙江金华人，硕士研究生，主要从事工程结构数值分析与优化方面的研究。通讯作者：张延庆教授。E-mail:zhyq@bjut.edu.cn

中图分类号：TU311.4

文献标志码：A

doi:10.7535/hbgykj.2016yx03008

陈斌，张延庆.广义协调COONS曲面厚薄板通用单元振动分析[J].河北工业科技,2016,33(3):224-229.

CHEN Bin, ZHANG Yanqing.Vibration analysis of generalized conforming and COONS’ surface thick/thin plate element[J].Hebei Journal of Industrial Science and Technology,2016,33(3):224-229.