多个部分相对整体异速生长的联合分析模型
周晓晶(黑龙江八一农垦大学理学院,大庆163319)
多个部分相对整体异速生长的联合分析模型
周晓晶
(黑龙江八一农垦大学理学院,大庆163319)
摘要:根据异速生长的数学原理并考虑多个体成分或组织器官生长间的相互关系,首先提出联合分析多个体成分或组织器官相对整体异速生长的数学模型;联合异速生长模型更有利于比较不同体成分或组织器官间异速生长的差异,并有利于分析体成分或组织器官相对整体异速生长的遗传基础。采用多元线性逐步回归分析方法估计模型的参数,分析了一个关于肉牛屠体性状的实际数据集,验证了所构建模型及所建议方法的有效性。
关键词:异速生长尺度;相关分析;联合分析;多元逐步回归分析
某些生物学特征和个体质量之间的关系可以用幂函数来表示,将其称为异速生长关系。自从Huxley 和Teissier[1]首次给出了这个概念以来,有关异速生长的研究报道层出不穷[2-12],涉及了动物生理、生长发育、遗传、进化和生态等多方面因素。描述组织器官间尺度相关的异速生长包括静态的、个体发育的和进化的异速生长三种类型:静态异速生长反映了在特定的发育阶段或者生长停滞以后不同性状间相对生长速度的差异,个体发育的异速生长是指生命过程中一个组织器官相对于另一个组织器官的生长轨迹间的关系,而进化的异速生长是不同品种或物种间相同性状的大小关系[13-14]。
在各种异速生长尺度关系中,最有影响力的当属机体代谢率与个体大小之间的“3/4幂率”,也就是后来生物学界著名的“Kleiber法则”[15]。以Kleiber法则为基础,生物学家相继又提出了不少的假说和相关模型,其中包括分形分布网络模型[5-7]、效率转运网络模型[16]、多因模型[17]、最小全部熵增模型[18]、结构理论假说[19]、细胞模型[20]和能量消耗模型[21]。尽管发育过程在保持性状间的功能尺度关系和进化方面发挥重要作用[13,22-23],但是研究者们对在体型上的个体发育变化的遗传结构及与之相关的异速生长知之甚少,部分原因是由于缺乏适宜的分析工具。只是在近20年,人们才大量应用几何形态测定法去研究机体形状是如何变化的,以及在个体发育过程中这些改变是如何与异速生长相关联的[24-26]。将这种方法应用于研究几种鱼的机体形态变化的个体发育,发现不是所有的体成分而是部分的体成分决定着个体发育[27]。然而这些研究都没有试图从发展的角度来探索个体发育异速生长的遗传机制。
研究基于静态和个体发育的异速生长的概念,提出联合异速生长尺度的分析方法,同时一并估计出多器官部分的异速生长指数。基于个体发育的异速生长是具有时间依从性的,因此个体的异速生长是用多元逐步回归分析整体与多个体成分和器官随着时间的改变量。在案例分析中,用所建议的异速生长模型拟合资源群体每个屠宰性状相对胴体重量的异速生长关系并估计异速生长系数。
1 方法
1.1静态异速生长尺度模型
Huxley和Teissier最早提出了简单异速生长模型:

其中,x是部分或组织器官的重量或大小;y是整体的重量或大小;b′是部分或组织器官的异速生长系数,反映了部分或组织器官相对整体的成熟程度。事实上

也就是说,异速生长系数实质是部分或组织器官的相对生长速度与整体的相对生长速度之比。令

那么,我们也可以用b描述部分或组织器官与整体间的异速生长关系,只不过b作为部分或组织器官的异速生长系数,其含义与b′相反。方程(3)可以改变为下面的形式:

解这个微分方程,可以建立一个新的异速生长模型:

若研究m个部分或组织器官相对于整体的异速生长,则可以构造这些部分或组织器官相对整体关于β(为了便于后面的比较说明,与b相区分)的m个微分方程:

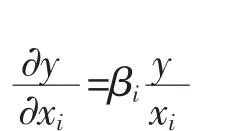

我们称这个模型为联合异速生长模型。βi(i=1,2,L,m)为机体第i个部分或组织器官相对整体的异速生长系数。它不但可以用来联合估计m个部分或组织器官相对于整体的异速生长系数,而且考虑了m个部分或组织器官之间的相互关系,更有利于统计比较不同部分或组织器官相对整体的异速生长系数。
实际应用中,通常对联合异速生长模型两边同时取自然对数,使其变为一个相对简单的线性模型
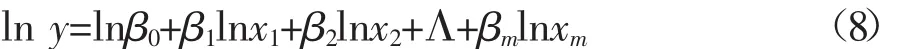
这样,采用多元线性模型最小二乘法便可估计模型的参数。
1.2联合分析多个静态异速生长的遗传模型
静态异速生长的估计是基于某个特定生长时间点,每个个体只有一个测量值。在简单单个性状动物模型的基础上,可以将整个体大小的对数剖分为:

其中,bj是第j个个体的固定效应项,ai是第i个个体加性遗传效应项,ωi是bj条件下的设计矩阵,ei是剩余误差效应,服从期望为零,方差为σ2e的正态分布。
为了进一步遗传分析多个部分体大小对整个体大小的异速生长指数,模型(8)被分别镶嵌进模型(9)的固定效应项和加性遗传效应项,得到下面的随机回归模型[28]:
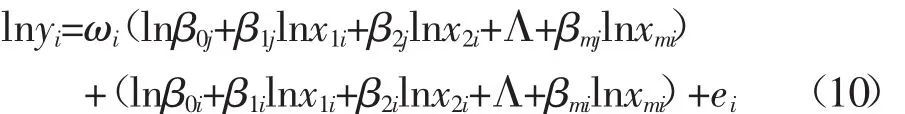
在指示矩阵下,模型(10)可以简化为:

2 实际例子分析——肉牛屠体性状静态异速生长研究
宰杀189头肉牛,测量宰前活重(y)和13个屠体性状,具体包括整个胴体重(x1)、净肉重(x2)、高档牛肉重(x3)、全身骨骼重(x4)、肌内脂肪重(x5)、红下水重(x6)、阴茎重(x7)、牛尾重(x8)、牛皮重(x9)、白下水重(x10)、肠系膜和网膜重(x11)、板油重(x12)和肾重(x13)。(在这里说明一下:所谓下水,即可食用的牲畜的内脏。屠宰业和餐饮业所说的白下水专指肚子(胃)和大小肠子;红下水则指除肚子(胃)和大小肠子以外的动物内脏,如心、肝、肺、腰、脾等。)

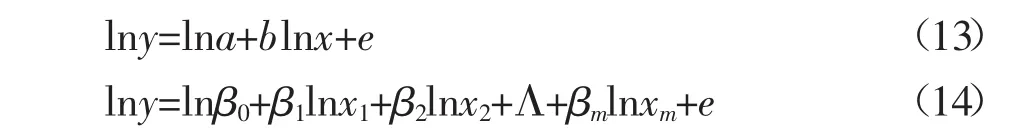
在进行分析之前,需对这些数据进行预处理,把宰杀肉牛的品种、饲喂日粮和月龄作为影响因子,对观测数据进行校正。为了更容易估计部分或组织器官相对整体的异速生长系数,对方程(1)、(5)和(7)两边同时做对数变换,得出以下三个线性模型:利用最小二乘参数估计法,分别计算模型的参数,即部分或组织器官相对于整体的异速生长系数。利用统计软件SAS分析测量性状间的相关性。部分或组织器官相对于整体的异速生长系数和肉牛活重与屠体性状的简单相关性以及他们的排序情况,分别列于下表1。

表1 肉牛异速生长系数的排序及组织或器官间的相关系数Table 1Ranking and correlations of allometric coefficients between tissues or organs for beef
b′即为Huxley和Teissier最早提出的简单异速生长模型中的部分或组织器官的异速生长系数,反映了部分或组织器官相对整体的成熟程度,见方程(1)。为了得到分析多个部分或组织器官相对于整体的异速生长模型,即联合异速生长模型—方程(7),由方程(2)推出方程(3)中的b,即整体的相对生长速度与部分或组织器官的相对生长速度之比,它也可以用来描述部分或组织器官与整体间的异速生长关系。r为肉牛宰前活重与13个屠体性状之间的相关系数,由统计软件SAS分析得到。
理论上,b与b′的关系应该具有相反的趋势,也就是说b升序排列的结果与b′做降序排列的结果相同。但是,从表中可以看到b与相对应的b′的顺序差异非常大,主要是由于屠体性状与宰前活重的相关程度的不同引起,也就是说是由b′b=r2中r造成的。考虑到屠体性状间的相关性,SAS中适用于拟合最优的异速生长模型参数的是多元逐步回归分析。建立的优化联合异速生长模型方程:
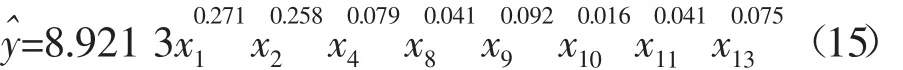
由方程可以看出,异速生长尺度系数符合统计显著水平的屠体性状分别是:胴体重(0.027 1)、净肉重(0.258)、骨骼重(0.079)、牛尾重(0.041)、牛皮重(0.092)、白下水重(0.116)、肠系膜和网膜重(0.041)、肾重(0.075)。
这8个屠体性状的协方差矩阵为:

3 讨论
(1)异速生长尺度关系用于描述一些变量随个体大小改变而变化的情况,这种关系在自然界中无所不在,其本质可以归结为有普遍存在系统的自相似性。包括有机体生理的、几何的和功能的相似性[23]。也就是说复杂系统的总体与部分,部分之间的精细结构或性质所具有的相似性,或者说从整体中取出的局部(局域)能够体现整体的基本特征,即几何变换下的不变性:在不同放大倍数上的性状相似。包括几何结构与形态、过程、信息、功能、性质、能量、物质(组份)、时间、空间等特征,具有自相似性。机体的生物学性状和功能都可以作为简单异速方程的因变量,其不仅包括个体某个部分的大小,还包括个体某个部分的形状、密度、体积、代谢率等等,都可以作为因变量进行异速生长关系的分析。在对机体代谢率进行异速关系分析时,Darveau等[17]在2002年提出了多因异速生长模型,主要要点是总代谢率可通过代谢路径的控制系数和多控制点的尺度系数来估计。如果同时测量代谢路径中的每个控制点的代谢率,那么我们所建立的的联合异速生长模型适用于分析每个控制点的代谢率与个体重间异速生长关系,从而更加深入的了解。更进一步的说,此模型适于联合分析相似或具有可比性的多个生物学性状和功能。
(2)关于畜禽异速生长的数学模型和统计分析方法的报道还没有见诸报端,更多的研究是关注生长发育性状的绝对生长。受以上方法启示,可以尝试将研究拓展到畜禽异速生长模型的构建,将关于多个体成分或组织器官相对整体大小的联合异速生长模型镶嵌到单个QTL的遗传效应中,构造用来检测控制异速生长基因位点的遗传模型。
(3)除了常规数量性状的关联分析与区间定位分析方法[29-32],考虑到生长性状表型的时空变化,可以采用针对多个测定点的多性状分析方法,关于多个QTL的更精确的确定(在基因组上的位置及表现的遗传效应),应考虑采用由Kao和Zeng提出的多重区间定位方法[33],特别应考虑由Yandell等提出的在同一时间鉴别多个QTL的功能强大的一系列贝叶斯模型[34-35]。此外,在发育过程中的异速生长的变化有可能反映功能变化以及形态与环境之间可能存在的关系,从而可以考虑将环境因素合并到异速生长模型中剖分QTL对这种关系的遗传效应。更全面的研究应该考虑到多种环境下[36]控制异速生长QTL的环境依赖性表达。
参考文献:
[1]Huxley J,Tessier G.Terminology of relative growth[J]. Nature,1936,137:780-781.
[2]Peters R H.The Ecological implications of body size[M]. Cambridge:Cambridge University Press,1983.
[3]Niklas K J.Plant Allometry:the scaling of formand process [M].Chicago:University of Chicago Press,1994.
[4]Niklas K J.Size-dependent variations in plant growth rates and the“3/4-power rule”[J].American Journal of Botany,1994,81(2):134-144.
[5]West G B,Brown J H,Enquist B J.A general model for the origin of allometric scaling laws in biology[J].Science,1997,276(5309):122-126.
[6]West G B,Brown J H,Enquist B J.A general model for structure and allometry of plant vascular systems[J].Na-ture,1999,400:664-667.
[7]West GB,Brown J H,Enquist B J.The fourth dimension of life:fractal geometry and allometric scaling of organisms [J].Science,1999,284,1677-1679.
[8]Dreyer O,Puzio R.Allometric scaling in animals and plants[J].Journal of Mathematical Biology,2001,43(2):144-156.
[9]Dodds P S,Rothman D H,Weitz J S.Re-examination of the“3/4-law”of metabolism[J].Journal of Theoretical Biology,2001,209(1):9-27.
[10]Enquist B J,Brown J H,West G B.Allometric scaling of plant energetics and population density[J].Nature,1998,395:163-165.
[11]Zelditch M L,Fink W L.Allometry and developmental integration of body growth in a piranha,Pygocentrus nattereri(Teleostei:Ostariophysi)[J].J Morphol,1995,223 (3):341-355.
[12]Reis R E,Zelditch M L,Fink W L.Ontogenetic allometry of body shape in the neotropical catfish Callichthys (Teleostei:Siluriformes)[J].Copeia,1998(1):177-182.
[13]Stern D L S,Emlen D J.The developmental basis for allometry in insects[J].Development,1999,126:1091-1101.
[14]Breuker J,Boer A,Hoekstra R,et al.Developing content for lkif:ontologies and frameworks for legal reasoning[J]. Jurix,2006,20:152.
[15]Kleiber M.Body size and metabolism[J].Hilgardia,1932,6(11):315-353.
[16]Banavar J R,Maritan A,Rinaldo A.Size and form in efficienttransportationnetwork[J].Nature,1999,399 (6732):130-132.
[17]Darveau C A,Suarez R K,Andrews R D,et al.Allometric cascade as a unifying principle of body mass effects on metabolism[J].Nature,2002,417(6885):166-170.
[18]Andresen B,Shiner J S,Uehlinger D E.Allometric scaling and maximum efficiency in physiological eigen time [J].Proc Natl Acad Sci,2002,99(9):5822-5824.
[19]Bejan A.Shape and Structure:from Engineering to Nature [M].New York:Cambridge University Press,2000.
[20]Kozlowski J,Konarzewski M,Gawelczyk A T.Cell size as a link between noncoding DNA and metabolic rate scaling[J].Proc Natl Acad Sci,2003,18:283-289.
[21]Makarieva A M,Gorshkov V G,Li B.A note on metabolic rate dependence on body size in plant and Animals[J]. Journal of Theoretical Biology,2003,221:301-307.
[22]West G B,Brown J H.The origin of allometric scaling laws in biology from genomes to ecosystems:towards a quantitative unifying theory of biological structure and organization[J].J Exp Biol,2005,208(9):1575-1592.
[23]Rombough P.Development rate-modelling developmental time and temperature[J].Nature,2003,424:268-269.
[24]Bookstein F L.Morphometric tools for landmark data:geometry and biology[M].New York:Cambridge University Press,1991.
[25]Rohlf F J.On applications of geometric morphometrics to studies of ontogeny and phylogeny[J].Syst Biol,1998,47 (1):147-158.
[26]Zelditch M L,Fink W L.Allometry and developmental integration of body growth in a piranha,Pygocentrus nattereri(Teleostei:Ostariophysi)[J].J Morphol,1995,223 (3):341-355.
[27]Reis RE,Zelditch ML,Fink WL.Ontogenetic allometry of bodyshapeintheneotropicalcatfishCallichthys (Teleostei:Siluriformes)[J].Copeia,1998,1:177-182.
[28]刘永新,杨润清.随机回归模型理论及其应用[J].东北农业大学学报,2008,39(2):265-270.
[29]Lander E S,Botstein D.Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps[J]. Genetics,1989,121(1):185-199.
[30]Zhou X J,Yan L,Yang R Y,et al.Characterization of genomic imprinting effects and patterns with parametric accelerated failure time model[J].Mol Genet Genomics,2012,287(1):67-75.
[31]Zhou XJ,Fang M,Yang RY,et al.Generalized F accelerated failure time model for mapping survival trait loci[J]. Genomics,2011,97(6):379-385.
[32]周晓晶,方铭.基于Cox半参数模型检测生存性状的印记数量性状位点[J].黑龙江八一农垦大学学报,2012,24(5):80-84.
[33]Kao C H,Zeng Z B,Teasdale R D.Multiple interval mapping for quantitative trait loci[J].Genetics,1999,152 (3):1203-1216.
[34]Yi NJ,Yandell B,Churchill G,et al.Bayesian model selection for genome-wide epistatic quantitative trait loci analysis[J].Genetics,2005,170(3):1333-1344.
[35]Yi N J,Shriner D,Banerjee S,et al.An efficient Bayesian model selection approach for interacting quantitative trait loci models with many effects[J].Genetics,2007,176 (3):1865-1877.
[36]Zhao W,Zhu J,Gallo-Meagher M,et al.A unified statistical model for functional mapping of genotype×environment interactions for ontogenetic development[J].Genetics,2004,168(3):1751-1762.
Joint Analysis Model for Allometric Relationship of Multiple Partial and Entire Body Size
Zhou Xiaojing
(College of Science,Heilongjiang Bayi Agricultural University,Daqing 163319)
Abstract:According to the mathematical principle of allometry and the allometric relationship of multiple partial and entire body size,the static allometry scaling model of entire body size on multiple partial body size was developed,which could not only simultaneously evaluate allometry scaling of multiple partial body size,but also take into account genetic basis allometry of multiple partial and entire body size.The multiple stepwise regression analysis was adopted to evaluate the parameters of the advised model. The proposed joint analysis method was illustrated in detail through a dataset for cattle.
Key words:allometry;correlation;joint analysis;multiple stepwise regression analysis
中图分类号:Q348
文献标识码:A
文章编号:1002-2090(2016)01-0113-05
doi:10.3969/j.issn.1002-2090.2016.01.025
收稿日期:2015-03-11
基金项目:肉牛异速生长模型的构建及统计分析方法的研究(201310223033);畜禽异速生长模型的全基因组关联分析(12531473)。
作者简介:周晓晶(1979-),女,副教授,北华大学毕业,现主要从事矩阵代数及生物数学的教学与研究工作。

