双块式无砟轨道温度场有限元模拟

毕澜潇，向　芬，丁晨旭，李　健，赵坪锐

（1.西南交通大学高速铁路线路工程教育部重点实验室，四川成都　610031；2.广州铁路（集团）公司广州工务段，广东广州　510000）



双块式无砟轨道温度场有限元模拟

毕澜潇1，向芬1，丁晨旭1，李健2，赵坪锐1

（1.西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031；2.广州铁路（集团）公司广州工务段，广东广州510000）

摘要无砟轨道大多采用钢筋混凝土材料筑成且长期暴露于空气中，由于混凝土的材料特性，其内部温度场会受到周围环境的影响，从而影响无砟轨道的服役性能。本文建立温度场模拟有限元模型，结合实测数据，研究了太阳辐射强度、大气日温差、风速等气象参数对无砟轨道温度场的影响。基于气象资料，对各地区无砟轨道最大温度梯度进行了预测。结果表明：通过有限元软件利用轨道周围的气象参数进行无砟轨道温度场计算分析可以满足工程精度要求；道床板顶、底面的最大日温差与大气日温差近似呈正比关系，太阳辐射和大气日温差是造成轨道温度梯度的主要原因；风速对轨道温度场的影响较气温和辐射小，当风速＞4 m/s时，轨道温度场对风速的变化不敏感。

关键词无砟轨道；温度场；有限元

无砟轨道结构大多由钢筋混凝土材料构成且长期暴露在大气中，其内部温度场除受混凝土材料自身热力学性能影响外，还随着外界气象因素的变化而不断改变，对轨道结构的承载能力和耐久性有着重要的影响［1-3］。因为受到气象因素和传热因素的双重影响，工程中边界条件和结构几何构造较复杂，应用解析法求解无砟轨道温度场较困难。现场试验虽能采集无砟轨道内部测点的温度，但其成本高、观测地点固定，不能满足分析大范围无砟轨道温度场特性的要求。大量学者在试验的基础上运用有限元数值方法进行模拟求解，以求得到无砟轨道温度场与气象参数的关系［4-5］。本文依托成都地区建立的CRTSⅠ型双块式无砟轨道实尺模型获得的大量轨道温度场数据［6］，运用有限元法建立温度场数值模型，探讨有限元法求解轨道温度场的可行性。分析了气象参数对无砟轨道温度场参数的影响，研究了在不同太阳辐射强度、大气日温差、风速等参数下轨道温度场的分布情况，并探寻一种基于气象参数的无砟轨道温度场预测的方法。

1　计算模型与参数

建立无砟轨道温度场有限元模型时，忽略对温度影响不大的双块式轨枕部分，采用实体单元模拟道床板和支撑层，有限元模型如图1。由现场试验获得的数据可知，基床温度的日变化很小，因而忽略路基层的影响。假设各层为完全均匀和各向同性的连续体，道床板和支撑层接触良好。

图1　无砟轨道板温度场有限元模型

无砟轨道温度场随时间而变化，为三维瞬态温度场，在瞬态分析之前须先定义温度场的初始条件，无砟轨道初始时刻结构内部温度分布不一致，需先取一段时间分析来定义结构初始温度［7］。即先选取3 d进行温度场瞬态热分析，以最后1 d的温度为瞬态分析初始条件。无砟轨道与环境间的热交换主要通过空气对流、太阳辐射以及热辐射3种形式［8］。空气对流用对流方式施加，将热辐射换热等效为对流换热，将太阳辐射热流密度换算成当量温度，得到空气综合温度，采用对流荷载来代替施加的方法，将综合气温和综合换热系数赋予轨道边界面上的节点［9-10］。时间步长取0. 5 h，计算时间24 h，混凝土的导热系数取3. 0 W /（m·K），比热取0. 95 kJ/（kg·℃）［11］。

2　模型验证

基于成都地区实测气象数据［6］，验证ANSYS模拟无砟轨道温度场的准确性，对轨道中不同测点进行了理论值与实测值的对比，见图2。

图2　温度计算值与实测对比

图2（a）为某观测日道床板板中位置表面实测温度和计算温度对比图，由图可知两者变化趋势相同且差异较小，大部分时间内两者吻合较好。实测最高温度35. 8℃，计算值35. 4℃，相差0. 4℃，最大误差不超过1. 5℃。图2（b）是相同观测日道床板内12. 5 cm深度处板角位置实测和计算温度对比图。板角位置两者变化趋势相同，计算值较实测值大，最大误差在3℃以内。

总体来看，基于气象资料利用有限元模型进行无砟轨道温度场模拟是可行的，满足工程要求。计算值与实测值存在误差的主要原因：①初始条件存在差异；②无砟轨道的热力学参数如换热系数、导热系数以及气象资料如风速等难以精确取值；③边界条件简化的影响以及混凝土材料的离散性、不均匀性等。

3　气象参数影响分析

无砟轨道直接暴露在大气中，气象参数的变化对内部温度场有显著影响。利用建立的有限元模型，分析了大气温度、太阳辐射、风速等气象参数对无砟轨道温度场的影响。

3. 1太阳辐射强度

分别考虑图3所示的不同季节太阳辐射强度，冬季晴天、春秋晴天、夏季晴天时太阳辐射峰值分别为275，517，856 W /m2。计算得到道床板温度变化如图4和表1所示。

图3　太阳辐射强度变化

图4　道床板温度变化

表1　不同太阳辐射强度下轨道最高温度分布　℃

由图4及表1可以看出，太阳辐射强度对无砟轨道内部温度场的影响很大，轨道内部各深度处温度以及顶面与底面温差随季节不同具有明显差异。太阳辐射对表层混凝土温度影响最强，与冬季相比春秋及夏季道床板表面温度分别增大了3℃和8. 8℃，道床板中部温度分别增大了1. 4℃和4. 7℃，道床板底部温差变化幅度也超过了1℃。分析数据发现，当太阳辐射强度每增大或减小100 W /m2时，道床板表面与底面温差增减约1. 5℃，对应的温度梯度增减约6℃/m。

3. 2日气温差

大气温度是无砟轨道温度场的主要影响因素之一，可通过不同日温差下温度场计算结果来分析气温对无砟轨道温度场的影响。将2013年10月12日的气温变化代入下式进行折算，以模拟不同的日气温差异

式中：T'i为变换后的实时气温为平均气温；Ti为实测气温；m为折算系数。

考虑3种工况：①m取0. 5，平均气温25. 3℃，日温差6℃；②m取1，平均气温25. 3℃，日温差12℃；③m取2，平均气温25. 3℃，日温差24℃。

图5为不同日温差下道床板顶面与板底温差对比图。大气日温差对轨道竖向温差产生显著影响，气温变化速率随日温差的增大而增大，引起的无砟轨道上下表面温差也将增大。由于上表面与空气直接接触，所以温度变化也随之加快，变化幅度也更大，而底面温度变化幅度相对较小，从而造成较大的上下表面温差。随着气温日温差从6℃增大到12℃和24℃，道床板板面与板底最大正温差分别从1. 6℃增大到3. 1℃和6. 2℃，几乎呈线性增长。大气日温差是造成道床板温度梯度的主要原因之一。

图5　不同日温差下道床板顶面与板底温差对比

3. 3风速

对流系数与风速基本呈线性关系，风速大小会对无砟轨道与其周围空气间的对流换热强弱产生影响［4］。假设不同风速对应不同的综合换热系数：工况1风速为0，对应的综合换热系数为11. 2，；工况2风速为2 m/s，对应的综合换热系数为19. 2；工况3风速为4 m/s，对应的综合换热系数为27. 2；工况4风速为6 m/s，对应的综合换热系数为35. 2；工况5风速为8 m/s，对应的综合换热系数为43. 2。不同风速时轨道温度场的计算结果如图6和图7。

图6　不同风速下道床板最高温度分布

图7　不同风速下板面与板底温差变化曲线

由图6和图7可知，随着风速的不断增大，混凝土道床板与周围空气热交换作用增强，板内各深度处的日最高温度逐渐降低，板面与板底温差也逐渐减小。当风速从0增大到4 m/s时，道床板表面最高温度减小了1. 7℃，而板底温度只减小了0. 6℃，板面与板底最大温差减小了1. 2℃，表明风速对道床板表层混凝土温度影响较大。各深度最高温度的变化率随风速的增大而减小，说明轨道温度受风速影响敏感程度随风速的增加而逐渐降低。风速对无砟轨道温度场的影响远小于太阳辐射和大气温度。

4　不同地区无砟轨道温度场预测

无砟轨道温度场主要受气象参数及混凝土热力参数的影响，由前文分析可知，当混凝土热力参数一定时，影响温度场分布特性的主要因素为大气温度和太阳辐射。基于我国典型地区的气象资料，利用前文建立的无砟轨道温度场有限元模型，对不同地区夏季高温时无砟轨道温度场进行模拟分析，通过气象资料预测无砟轨道温度场特性。

4. 1气象资料处理

各地区整点气温可以通过气象局获取，但各地区太阳辐射差异较大，且从气象局获取的太阳辐射强度主要为日太阳总辐射，需要对其进行处理才能用于本文模型的计算。

通过太阳常数、太阳倾角、太阳时角、太阳高度角、太阳方位角、太阳入射角等参数计算得出太阳直接辐射IDφ和太阳散射辐射Idβ。由太阳直接辐射和太阳散射辐射，可以计算出晴天时任意方向的结构所受到的太阳总辐射强度［12］，即

轨道板水平表面外法线相对于水平面的夹角βn= 90°，所以cosφ= sinβs，则总辐射为

对于轨道竖直平面cosφ= cosβscos（αn-αs），βn= 0°，总辐射为

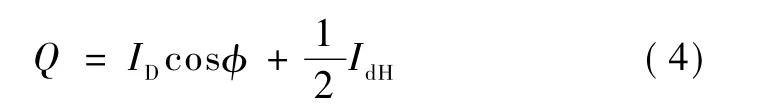
式中：φ为太阳入射角；βs为太阳高度角；ID为太阳直接辐射强度；IdH为太阳散射辐射强度；βn为太阳射入线与轨道板某面的角度。

4. 2温度场预测分析

我国无砟轨道分布地区广，气候差异大，本文取5个典型地区进行无砟轨道温度场计算分析。分别为成都、乌鲁木齐、上海、广州、哈尔滨。各地区气温和太阳辐射强度数据范围取为2014年6月15日至2014年8 月15日，成都和乌鲁木齐的数值见图8。

图8　2014年夏季气温和太阳辐射强度变化

限于篇幅，文中仅列出部分数据及结果。以成都及乌鲁木齐地区为例，成都地区夏季日最高温度平均值在28～30℃，太阳辐射较弱，气温相对稳定；乌鲁木齐地区，夏季日最高温度平均值＞34℃，且太阳辐射较强，昼夜温差较大。

利用以上气象数据，和本文建立的无砟轨道温度场有限元模型计算得到了成都、乌鲁木齐等地区2014年夏季轨道温度场数据，如图9。

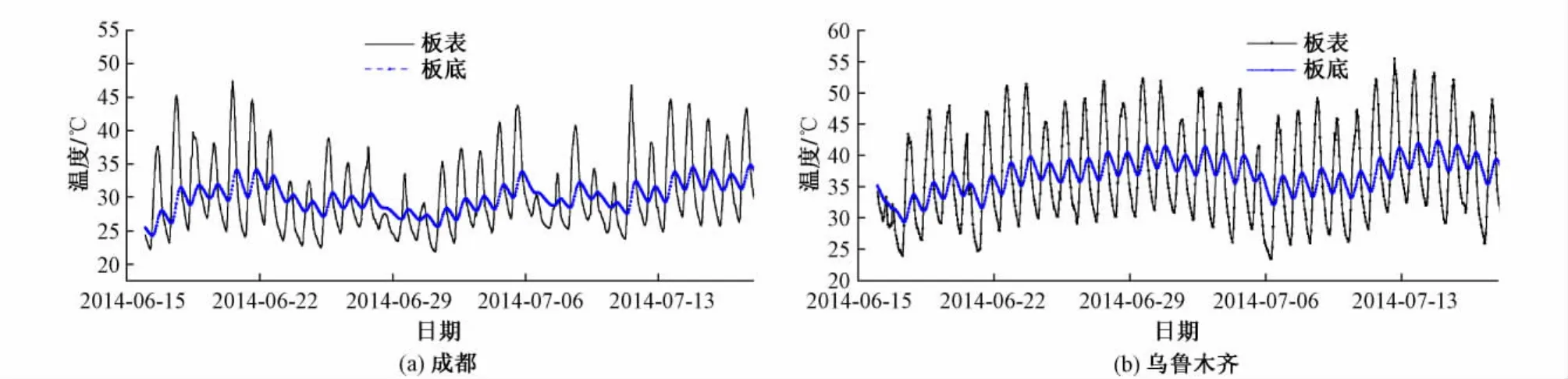
图9　2014年夏季道床板温度变化

2014年成都地区夏季平均气温较历年高，在25℃左右，最高气温37℃，最低气温17℃。经有限元模拟得到的道床板表面最高、最低温度分别为51. 1℃，21. 3℃；距离道床板顶面25 cm深度处最高温度38. 8℃，最低温度24. 3℃。道床板各层平均温度在31. 5℃左右，但表面受外界气象因素影响较大，温度变化幅度达到了30℃，板底温度变化幅度达到15℃左右。

2014年乌鲁木齐地区夏季平均气温为27℃，最高气温37℃，最低气温14℃，昼夜温差较大，天气以晴天为主，太阳辐射较强。道床板表面最高温达到55. 5℃，最低温度为20. 5℃；道床板底面距顶面25 cm深度处最高温度43℃，最低温度27. 8℃。板表面温度变化幅度达到35℃，较成都地区高，板底温度变化幅度达到15℃左右。

图10是根据计算得到的两地区2014年夏季道床板温度梯度变化趋势图，各地区温度梯度极值统计结果如表2所示。

图10　2014年夏季道床板温度梯度变化

表2　各地区2014年夏季道床板温度梯度统计结果

经计算得到的成都地区夏季最大温度梯度为80℃/m，实测夏季温度梯度最大值为78℃/m［6］，较为符合。计算所得各地区最大正温梯度均达到80℃左右，尤其是乌鲁木齐地区，由于昼夜温差大，太阳辐射较强，最大正温度梯度达到了91℃/m，夏季最大负温度梯度也达到30℃。同时在2014年6月16日至2014年8月15日的61 d中，各地区日温度梯度极值超过45℃/m的天数均超过了30 d，上海地区由于夏季雨天较多，日温度梯度极值超过45℃/m的天数相对较少，而乌鲁木齐地区夏季以晴天为主，辐射较强且日温差大，所以日温度梯度极值超过45℃/m的天数达到了53 d。

5　结论与建议

通过ANSYS有限元软件对无砟轨道试验段温度场进行计算，并对比分析计算值与实测值，结论如下：

1）有限元计算值与实测无砟轨道温度值两者的吻合程度较高，可以得到满足工程精度要求的计算结果，说明通过有限元模型利用轨道周围的气象参数进行无砟轨道温度场计算分析是可行的。

2）太阳辐射对无砟轨道温度场影响非常明显，当太阳辐射强度每变化100 W /m2时，道床板顶、底面温差大约对应变化1. 5℃，对应的温度梯度变化6℃/m。

3）大气温度对轨道温度场的影响主要表现在日温差上，道床板顶、底面的最大日温差与大气日温差近似呈正比关系，太阳辐射和大气日温差是造成轨道温度梯度的主要原因。

4）在没有进行实测试验的情况下，基于某地获取的整点气温和太阳辐射强度气象资料，利用有限元软件可以对当地温度场特性进行预估，为无砟轨道强度设计提供依据。

参考文献

［1］刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法［M］.成都：西南交通大学出版社，2010：106-110.

［2］王继军，尤瑞林，王梦，等.单元板式无砟轨道结构轨道板温度翘曲变形研究［J］.中国铁道科学，2010，31（3）：9-14.

［3］邵丕彦，李海燕，吴韶亮，等. CRTSⅠ型轨道板温度变形及与砂浆垫层间离缝的测试研究［J］.中国铁道科学，2013，34（2）：18-22.

［4］张澜.温度作用下双块式无砟轨道道床板有限元分析［D］.武汉：武汉理工大学，2009.

［5］李健，赵坪锐，万章博，等.双块式无砟轨道温度场试验研究和数值分析［J］.中国科学：技术科学，2014，44（7）：729-735.

［6］赵坪锐，李健.无砟轨道温度场报告［R］.成都：西南交通大学，2014：1-44.

［7］肖本伟.王坡沟大桥温度效应分析和黄土湿陷性试验研究［D］.重庆：重庆大学，2013.

［8］欧祖敏，孙璐，程群群.基于气象资料的无砟轨道温度场计算与分析［J］.铁道学报，2014，36（11）：106-112.

［9］苑红凯.含裂缝沥青路面结构力学性能研究［D］.南京：东南大学，2006.

［10］孟庆峰.李立增.时雪梅.悬臂施工的预应力箱梁温度场分析［J］.铁道建筑，2010（7）：14-18.

［11］聂玉东.寒区大跨径混凝土箱梁桥温度场及温度效应分析［D］.哈尔滨：哈尔滨工业大学，2013.

［12］彭友松.混凝土桥梁结构日照温度效应理论及应用研究［D］.成都：西南交通大学，2007.

（责任审编赵其文）

第一作者：毕澜潇（1988—），男，硕士研究生。

Finite Element Simulation of Temperature Field in Double-block Ballastless Track

BI Lanxiao1，XIANG Fen1，DING Chenxu1，LI Jian2，ZHAO Pingrui1
（1. MOE Key Laboratory of High-speed Railway Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China；2. Track Division of Guangzhou，Guangzhou Railway（Group）Corporation，Guangzhou Guangdong 510000，China）

AbstractBallastless track is made of reinforced concrete material and exposes to air for a long period. T he inner temperature field is affected by surrounding environmental conditions due to material properties of concrete，which could affect the service performance of ballastless track. A finite element model of temperature field simulation was built and the effect of meteorological parameters including solar radiation intensity，atmospheric diurnal temperature and wind speed on temperature field of ballastless track was studied by combining with the measured data. Based on meteorological data，the maximum temperature gradient of ballastless track in each region was forecasted. T he results show that the temperature field of ballastless track is calculated by finite element software and using meteorological parameters around the track，which could meet the requirements of engineering precision. T here is an approximate proportional relation between maximum daily temperature difference and daily temperature difference of slab top and bottom，solar radiation and atmospheric diurnal temperature are the main reasons of the track temperature gradient while wind speed has a smaller effect on the track temperature field than effect of temperature and radiation，the track temperature field is not sensitive to the change of the wind speed when the wind speed is above 4 m /s.

Key wordsBallastless track；T emperature field；Finite element

中图分类号U213. 2+44

文献标识码A

DOI：10. 3969 /j. issn. 1003-1995. 2016. 05. 08

文章编号：1003-1995（2016）05-0034-06

收稿日期：2016-02-04；修回日期：2016-03-07

基金项目：国家重点基础研究发展计划（973计划）课题（2013CB036202）；国家自然科学基金（U1434208）；中国铁路总公司科技研究开发计划（Z2013G001，2014G001-A）

通讯作者：赵坪锐（1978—），男，副教授，博士。