The Riemann Problem with Delta Data for Zero-Pressure Gas Dynamics∗
Li WANG
1 Introduction
In this paper,we are concerned with the one-dimensional system of conservation laws of mass,momentum and energy in zero-pressure gas dynamics characterized by
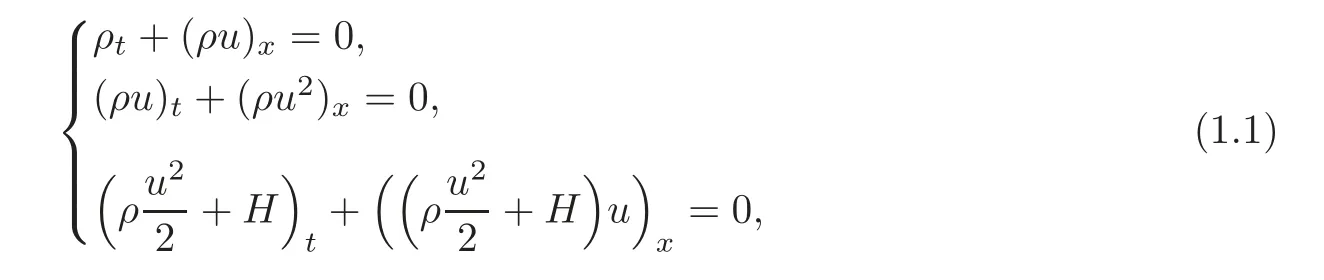
where ρ and u represent the density and velocity,respectively,H= ρτ is the internal energy,τ is the internal energy per unit mass.The zero-pressure gas dynamics system is a very important one to approach the full Euler equations,which can describe the motion of free particles which stick under collision and explain the formation of large-scale structures in the universe(see[1–2]).The zero-pressure gas dynamics system consisting of conservation laws of mass and momentum has been investigated extensively.For related results,see[3–8]and the papers cited therein.However,it is well known that for the media which can be considered as having no pressure,we must take into account energy transport.Therefore it is very necessary to consider the energy conservation law in zero-pressure gas dynamics(see[9–10]).
For the Riemann problem of system(1.1),it is not difficult to see that the delta shock and vacuum do occur(see[9]).In this paper,we will investigate the Riemann problem with delta initial data and possible interactions of delta shock waves and contact vacuum state for system(1.1).As for delta shock waves,we refer readers to[11–17]and the references cited therein for more details.
In this article,we first consider the Riemann problem for(1.1)with initial data
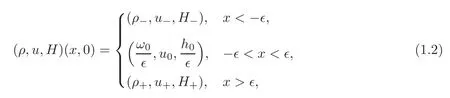
where?>0 is sufficiently small.We constructively obtain the solutions for the problem(1.1)–(1.2).Moreover,a new kind of nonclassical wave is obtained,namely,a delta contact discontinuity,which is a Dirac delta function supported on a contact discontinuity.Let?→0,under the stability theory of weak solutions,we obtain solutions for the system(1.1)with delta initial data

where δ is the standard Dirac delta function.With the help of generalized Rankine-Hugoniot conditions and the entropy condition,we obtain the global existence of generalized solutions for the problems(1.1)with(1.3).Moreover,if we let ω0=0,u0=0 and h0=0,the solutions of(1.1)with(1.3)correspond to the solutions of Riemann problem for(1.1).This method has been used in[18]to study the Riemann problem with delta initial data for the 1-D Chaplygin gas equations.
This paper is organized as follows.In Section 2,we recall and present some known results about the system(1.1)and its Riemann solution with constant initial data.In Section 3,we construct solutions of(1.1)–(1.2)case by case.Then letting? → 0,we obtain the generalized solutions of(1.1)with(1.3).
2 The Riemann Problem with Constant Initial Data
In this section,we study solutions of system(1.1)by considering the Riemann problem with initial data
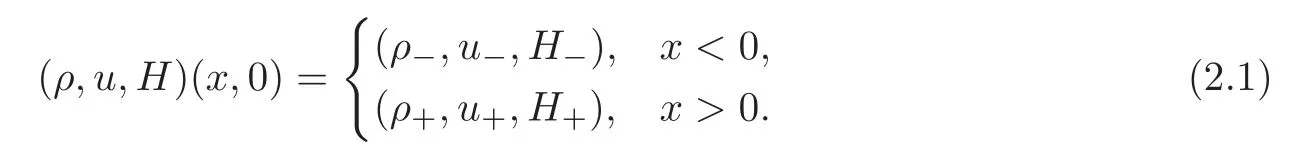
The details can be found in[9].The system(1.1)has a triple eigenvalue λ=u and two right eigenvectors r1=(1,0,0)Tand r2=(0,0,1)T,which satisfy∇λ·ri=0,i=1,2.Thus the system(1.1)is linearly degenerate.Furthermore,we obtain the Riemann solutions of(1.1)with(2.1)containing contact discontinuities,vacuum or delta shock wave.
For the case u−≤u+,the solution can be expressed as
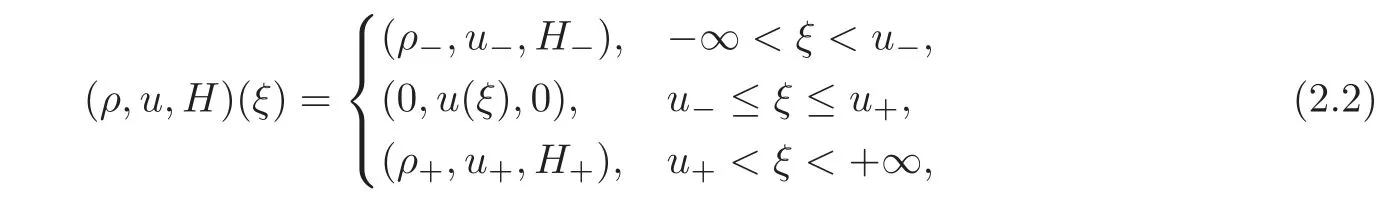
where u(ξ)satisfies that u(u−)=u−and u(u+)=u+(see Figure 2.1).
For the caseu−>u+,the overlap of the characteristic results in aδ-wave connecting the two states(ρ−,u−,H−)and(ρ+,u+,H+).The solution of(1.1)with(2.1)is

wherex(t),ω(t),h(t)anduδsatisfy the generalized R-H conditions
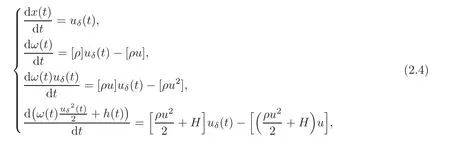
where[ρ]=ρ+− ρ−,with initial datax(0)=0,ω(0)=0,h(0)=0.By simple calculation,we obtain
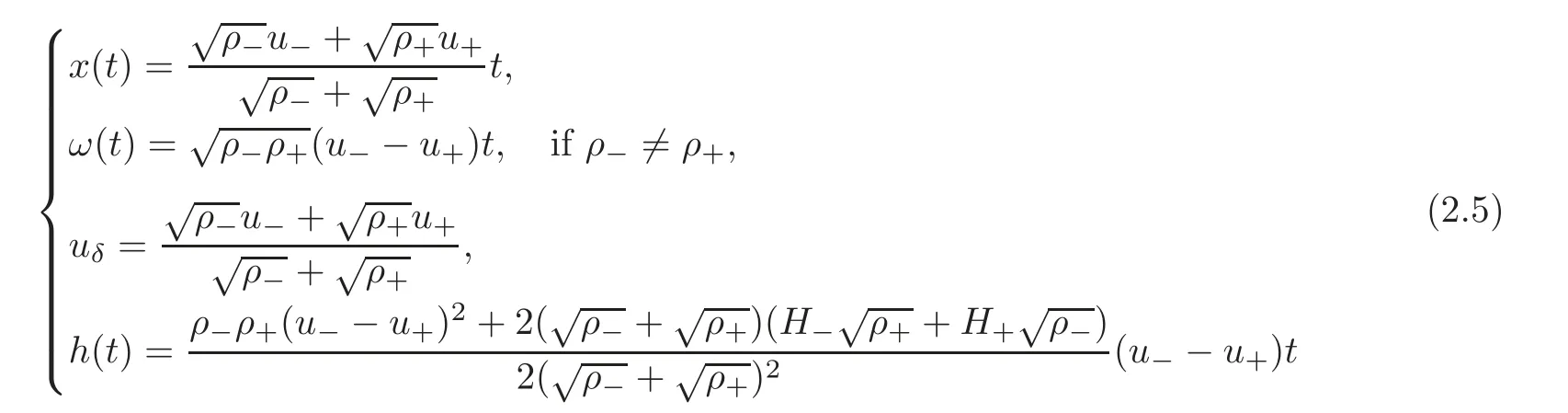
and

Thus,we have obtained the solutions of system(1.1)with(2.1).
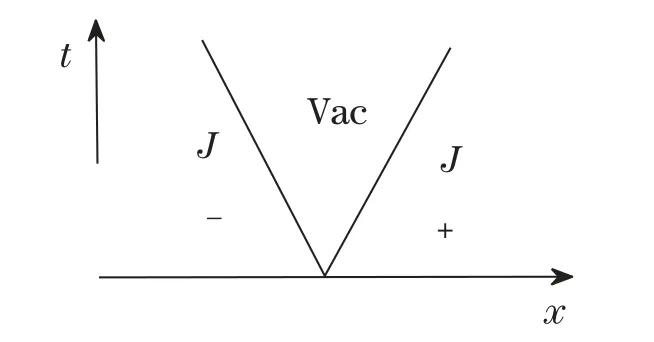
Figure 2.1 u− ≤u+
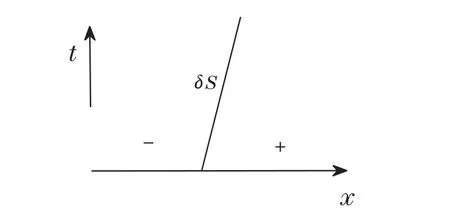
Figure 2.2 u−>u+
3 The Riemann Problem With Delta Initial Data
In this section,we first consider the solution to system(1.1)with(1.2).Then letting?→0,we get the solution of(1.1)with(1.3)under the stability theory of weak solutions.According to the relations amongu−,u+andu0,we discuss the Riemann problem case by case.
Case 1u−≤u0≤u+
In this case,whentis small enough,the solution of the initial value problem(1.1)–(1.2)can be expressed briefly as follows(see Figure 3.1(a)):
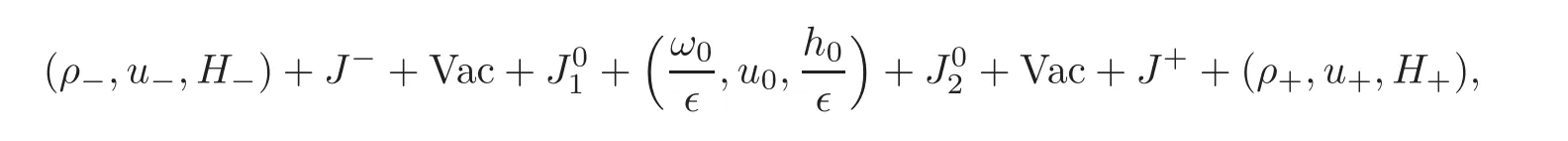
where“+” means“followed by”.The propagation speed of theandisu0.Thus we see that thecan not overtakeJ02at a finite time.So far,the solutions of(1.1)with(1.2)have been constructed completely.Letting?→0,we obtain a solution of(1.1)with(1.3)as follows(see Figure 3.1(b)):

where the propagation speed of theδSisu0.
Ifω0=0,u0=0 andh0=0,it is easy to see that the solution of(1.1)with(1.3)is consistent with the Riemann solutions of(1.1)with(2.1),which implies that the solution is stable with respect to the perturbation in this case.
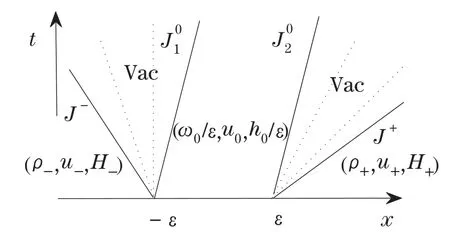
Figure 3.1(a)

Figure 3.1(b)
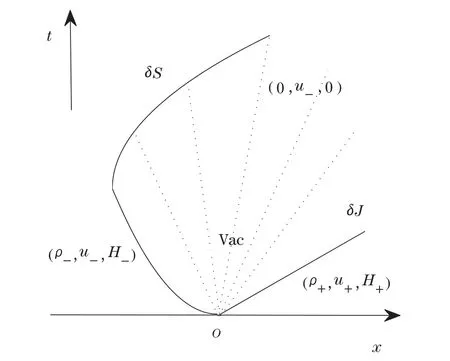
Case 2u0 Similarly to the analysis in Case 1,we seek the solution of the following form(see Figure 3.2): andδSsatisfies the following generalized Rankine-Hugoniot conditions: where[ρ]=0−ρ−,with initial data For more details,we refer readers to[18–19]and the references cited therein. Figure 3.2 Next,we only need to solve the initial value problem(3.2)with(3.3).From(3.2),we have and By virtue of(3.4)–(3.5),we have Solving(3.7)withω(0)=ω0,we have From(3.4)and(3.7),we have Using(3.5)–(3.6)and(3.8)–(3.9),we obtain Remark 3.1 From(3.9),we have This implies thatδSdoes not penetrate vacuum completely and it converts toδJwhent→∞. Remark 3.2 From(3.4),(3.6)and(3.8),ifω0=0,u0=0,h0=0,then(ω,u,h)=(0,u−,0).This is consistent with the results of the Riemann problem(1.1)with(2.1).It implies that the solution constructed here is stable under some perturbations. Case 3u+ Similarly to the analysis in Case 1,we seek the solution of the following form(see Figure 3.3): andδSsatisfies the following generalized Rankine-Hugoniot conditions: where[ρ]=ρ+−ρ−,with initial data Figure 3.3 Now,we are going to solve the initial value problem(3.13)with(3.14). Integrating(3.13)from 0 totwith initial data(3.14),we have Canceling ω in the first and second equation of(3.5),we have Integrating(3.16)from 0 to t,we have Solving(3.17),we get and From(3.15),we have and Remark 3.3 It is seen that So from(3.22),we have Remark 3.4 If ω0=0,u0=0,h0=0,then This is consistent with the results of the Riemann problems(1.1)with(2.1).It implies that the solution constructed here is stable under some perturbations. Case 4u0 Similarly to the analysis in Case 2,we know that,in this case,whentis small enough,the solution is the same as that in Case 2.More precisely,according to(3.9),there exists a uniquet1,such thatuδ(t1)=u+. When 0≤t≤t1,the solution is the same as that in Case 2.Whent>t1,theδ-shock wave will overtakeJ+in finite timet=t2,and we seek the solution of the following form(see Figure 3.4): Figure 3.4 For 0≤t≤t1,the solution is the same as that in Case 2,and here we omit the details. Fort1≤t≤t2, andδS1satisfies the following generalized Rankine-Hugoniot conditions: where[ρ]=0−ρ−,with initial data wherex1=x(t1),ω1=ω(t1),u1=u(t1)andh1=h(t1).The solution of(3.26)–(3.27)(x1,ω1,u1δ,h1)(t)can be obtained similarly as in Case 2. Fort>t2,wheret2is determined byx1(t2)=u+t2, and δS2satisfies the following generalized Rankine-Hugoniot conditions where[ρ]= ρ+− ρ−,with initial data where x2=x1(t2), ω2= ω1(t2),u2=u1(t2)and h2=h1(t2).The solution of(3.29)–(3.30)(x2,ω2,u2δ,h2)(t)can be obtained similarly as in Case 3. So far,we have finished the discussion for all kinds of interactions.We summarize our results in the following. Theorem 3.1 The solution of(1.1)with(1.3)can be obtained by letting?→0 for the solutions of(1.1)with(1.2).If we let ω0=0,u0=0,h0=0,the solution of(1.1)with(1.3)corresponds exactly to the solution of Riemann problem(1.1)with(2.1).It implies that the solution constructed here is stable under some perturbation. AcknowledgementThe author would like to thank the referees for their comments which helped to improve and clarify this paper. [1]Rykov,E.W.,Yu,G.and Sinai,Y.G.,Generalized variational principled,global weak solutions and behavior with random initial data for system of conservation laws arising in adhesion particle dynamics,Comm.Math.Phys.,177,1996,349–380. [2]Shandarin,S.F.and Zeldovich,Y.B.,The large-scale structure of the universe:Turbulence,intermittency,structure in a self-gravitatuing medium,Rev.Mod.Phys.,61,1989,185–220. [3]Bouchut,F.,On zero pressure gas dynamics,advances in kinetic theory and computing,Series on Advances in Mathematics for Applied Sciences,Vol.22,World Scientific,Singapore,1994. [4]Chen,G.Q.and Liu,H.L.,Formation of delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations,SIAM J.Math.Anal.,34,2003,925–938. [5]Sheng,W.C.and Zhang,T.,The Riemann problem for transportation equation in gas dynamics,Mem.Amer.Math.Soc.,137(654),1999,1–77. [6]Wang,Z.and Ding,X.,Uniqueness of generalized solution for the Cauchy problem of transportation equations,Acta Mathematica Scientia,173,1997,341–352. [7]Wang,Z.and Zhang,Q.L.,Spiral solutions to the two-dimensional transport equations,Acta Math.Appl.Scientia,306,2010,2110–2128. [8]Yang,H.,Generalized plane delta-shock waves for n-dimensional zero-pressure gas dynamics,J.Math.Anal.Appl.,260,2001,18–35. [9]Cheng,H.J.,Riemann problem for one-dimensional system of conservation laws of mass,momentum and energy in zero-pressure gas dynamics,Differential Equations and Applications,4(4),2012,653–664. [10]Kraiko,A.,Discontinuity surfaces in medium without self-pressure(in Russian),Prikladnaia Matematikai Mekhanika,43,1979,539–549. [11]Korchinski,D.J.,Solutions of a Riemann problem for a system of conservation laws possessing no classical weak solution,Adelphi University,1977. [12]Li,J.,Zhang,T.and Yang,S.,The Two-Dimensional Riemann Prolem in Gas Dynamics,Pitman Monogr.Surv.Pure Appl.Math.,98,Longman Scientific and Technical,London,1998. [13]Danilov,V.G.and Shelkovich,V.M.,Delta-shock waves type solution of hyperbolic systems of conservation laws,Quart.Appl.Math.,63,2005,401–427. [14]Guo,L.H.,Sheng,W.C.and Zhang,T.,The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system,Communications on Pure and Applied Analysis,9,2010,431–458. [15]Nedeljkov,M.and Oberguggenberger,M.,Interactions of delta shock waves in a strictly hyperbolic system of conservation laws,J.Math.Anal.Appl.,344,2008,1143–1157. [16]Shen,C.and Sun,M.,Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model,J.Differential Equations,249,2010,3024–3051. [17]Tan,D.,Zhang,T.and Zheng,Y.,Delta shock waves as limits of vanishing viscosity for hyperbolic system of conservation laws,J.Differential Equations,112,1994,1–32. [18]Wang,Z.and Zhang,Q.L.,The Riemann problem with delta initial data for the one-diemensional Chaplygin gas equations,Acta Mathematica Scientia,3,2012,825–841. [19]Shen,C.and Sun,M.,Interactions of delta shock waves for the transport equations with split delta functions,J.Math.Anal.Appl.,351,2009,747–755.
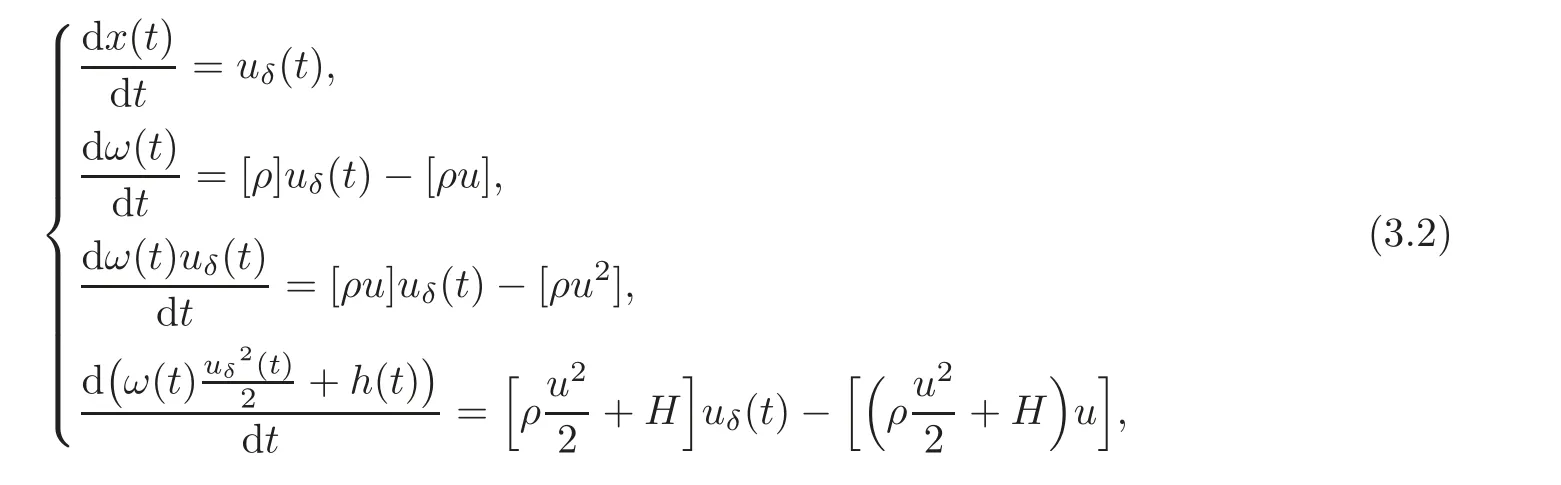


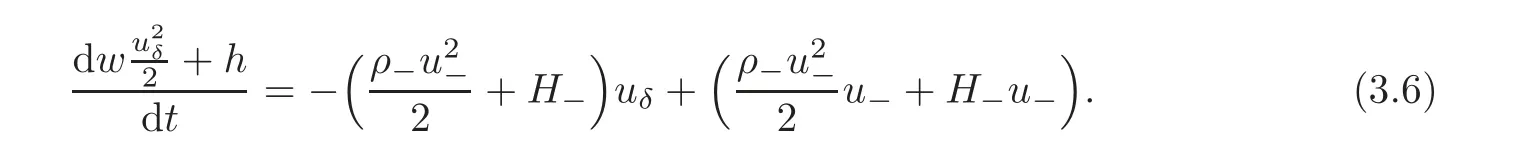

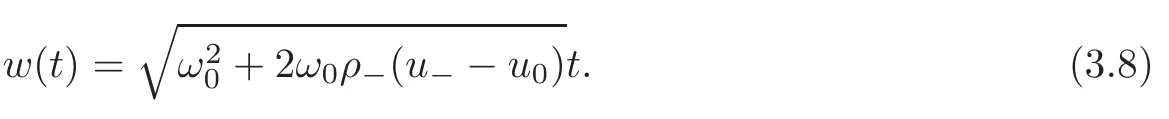
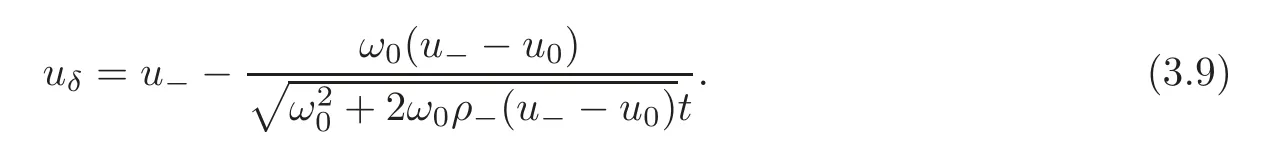


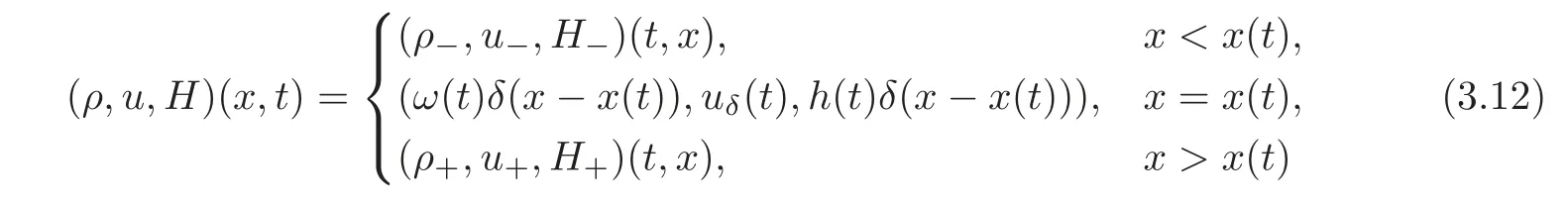
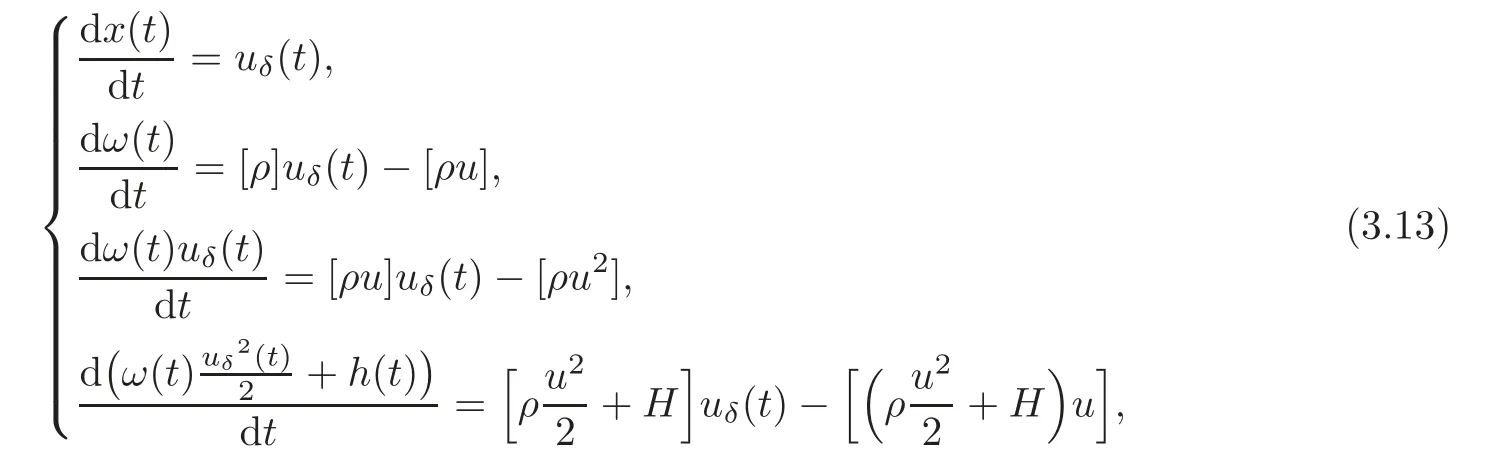


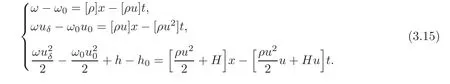

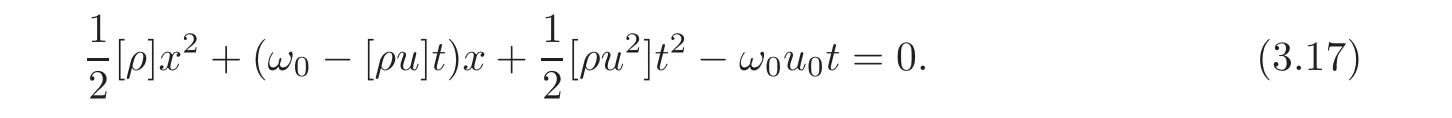
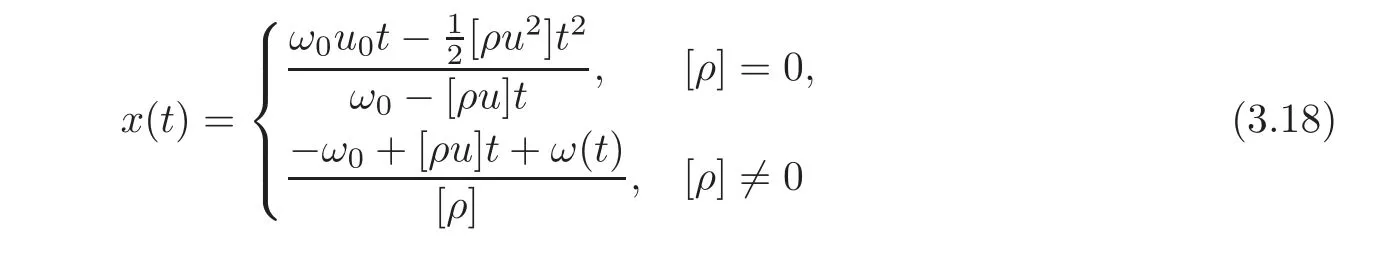

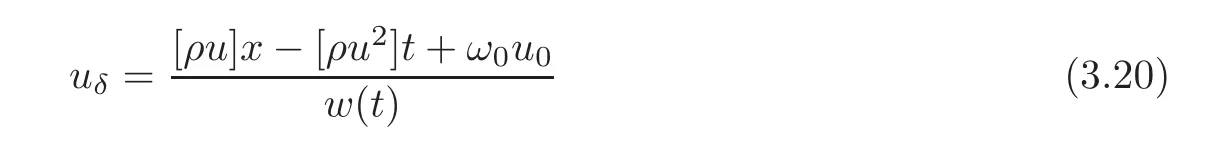



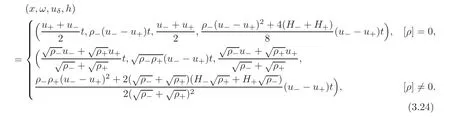

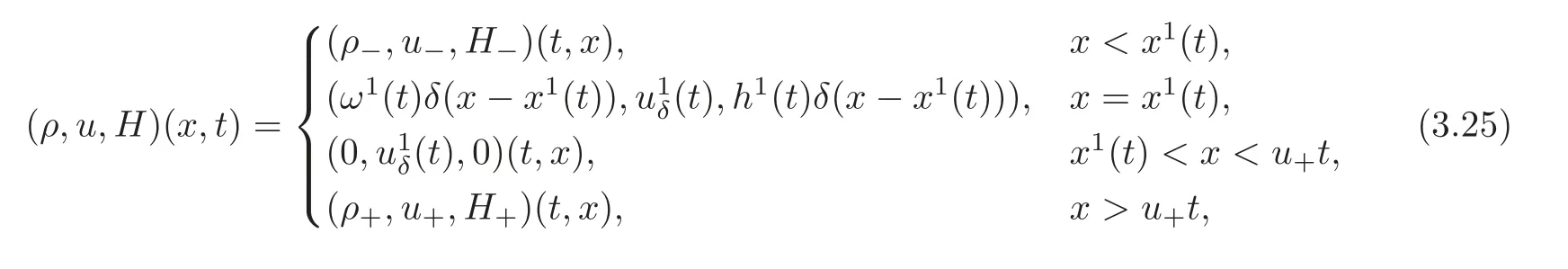

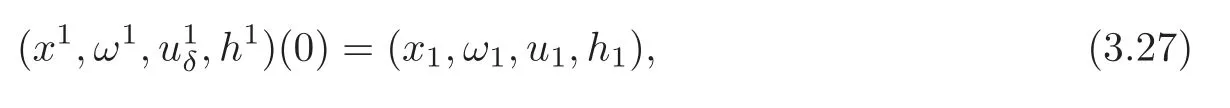



 Chinese Annals of Mathematics,Series B2016年3期
Chinese Annals of Mathematics,Series B2016年3期
